
HybridSLAM: A Robust Algorithm for Simultaneous Localization
and Mapping
Amir Monjazeb
1
, Jurek Z. Sasiadek
1
and Dan Necsulescu
2
1
Department of Mechanical and Aerospace Engineering, Carleton University, 1125 Colonel By Drive, Ottawa, Canada
2
Department of Mechanical Engineering, Ottawa University, 161 Louis Pasteur, CBY A205, Ottawa, Canada
Keywords: Simultaneous Localization and Mapping (SLAM) Problem, Unscented HybridSLAM, Unscented Kalman
Filter, Position Error, Time and Measurement Update.
Abstract: This paper addresses an ongoing research on a novel approach to Simultaneous Localization and Mapping
problem called Unscented HybridSLAM. The main contribution of this paper is to develop the map update
formulas along with proof results in order to investigate the validation of the map evolution. The
investigation is presented using the help of simulations in terms of robustness, map fusion, and the update
process. Results clearly show that as the vehicle travels along the path and the map evolves, the Unscented
HybridSLAM algorithm avoids the overestimation of landmarks.
1 INTRODUCTION
Simultaneous localization and mapping (SLAM) is
well known navigation technique for quite some
time (Smith, Cheesman, 1986). It is more than 2
decades that different aspects of SLAM are
identified and examined using many different
algorithms (Durrant-Whyte, Bailey, 2006). Such
algorithms are used to solve SLAM problem in
terms of ambiguity in data association and
complexity in computation (Monjazeb et al., 2012).
After all, the challenge is to avoid
under/overestimation of path and objects in the
environment. Amongst all solutions to SLAM
problem, different versions of FastSLAM
(Montemerlo, Thrun, 2003) and a few extensions of
Kalman filter are the pioneers (Bailey, 2002). For
instance, EKF-SLAM is accepted as the gold
standard solution, nevertheless, under some
limitations and specific circumstances. In order to
overcome such limitations, there are some combined
algorithms such as HybridSLAM (Brooks, 2009)
that by the use map fusion techniques (Williams, et
al, 2002) may be able to produce more reliable
maps. In some situations, such combined filters may
be superior to their counterparts. For instance, in a
large environment with huge amount of landmarks,
HybridSLAM outperforms FastSLAM based
algorithms. In this study a combined filter called
Unscented HybridSLAM and (as a combination of
HybridSLAM and Unscented Kalman Filter) is
represented. Then, map updating process is
theoretically probed and formulated. After all,
simulation of different scenarios will be presented
and the mapping update steps, robustness, and
different stages of map fusion process will be
thoroughly investigated and discussed. The
estimation of the mean and covariance of the
proposed algorithm will be analyzed and the results
will be compared with currently used algorithms.
2 UNSCENTED HYBRIDSLAM
ALGORITHM
Same as HybridSLAM (HS), the proposed algorithm
is a combination of FastSLAM and an extension of
Kalman filter. In Unscented HybridSLAM
(Monjazeb et al., 2014) however, the unscented
Kalman filter plays a role of estimating the global
map and getting updated once a local map is
estimated by FastSLAM. Naturally, UHS inherits all
properties of its subordinate filter UKF. As a matter
of fact, UHS does not suffer from the inconsistency
of EKF-SLAM the way HS does. Furthermore, UHS
is able to more properly handle the non-linearity of
the system than HS. By the help of a map-fusion
technique, UHS would be able to outperform EKF-
267
Monjazeb A., Sasiadek J. and Necsulescu D..
HybridSLAM: A Robust Algorithm for Simultaneous Localization and Mapping.
DOI: 10.5220/0005535802670274
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 267-274
ISBN: 978-989-758-123-6
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

SLAM, FastSLAM, and HybridSLAM. This
superiority in performance specifically lies in the
heart of the algorithm where time and measurement
processes are carefully updated without any
ambiguity. Moreover, UHS stays robust to cluttered
environments (Monjazeb et al., 2011).
3 TIME AND MEASUREMENT
UPDATE PROCESS
The first step is to initialize the position of the robot
at time zero, the covariance matrix of the system,
and noise in motion and observation as well as their
covariance matrices.
]E[
00
xx
ˆ
])-)(-E[(
0000x
k
T
ˆˆ
xxxxP
(1)
(2)
for k = 1 … ∞
(3)
The covariance square-root column vectors for time
–update [10] are
i
ix,
1-k
1-k
x
Ps
i = 1, 2, … , L
x
(4)
i
k
iw,
1-k
Qs
i = 1, 2, … , L
w
(5)
The time-update equations are
),,
ˆ
(f
LL
ˆ
1-kk1-k
wx
-
k
uwxx
2
2
][
2
1
1
2
)
ˆ
(f)
ˆ
(f
1-kk
ix,
1-k1-k
L
i
1-kk
ix,
1-k1-k
x
u,w,sxu,w,sx
][
2
1
1
2
)
ˆ
(f)
ˆ
(f
1-k
iw,
1-kk1-k
L
i
1-k
iw,
1-kk1-k
w
u,sw,xu,sw,x
(6)
2
1
2
x
][
4
1
k
)
ˆ
(f)
ˆ
(f
1-kk
ix,
1-k1-k
L
i
1-kk
ix,
1-k1-k
-
x
u,w,sxu,w,sxP
2
1
2
][
4
1
)
ˆ
(f)
ˆ
(f
1-k
iw,
1-kk1-k
L
i
1-k
iw,
1-kk1-k
w
u,sw,xu,sw,x
2
1
2
2
]),,
ˆ
(2
)
ˆ
()
ˆ
([
4
1
1-kk1-k
1-kk
ix,
1-k1-k
L
i
1-kk
ix,
1-k1-k
f
ff
x
uwx
u,w,sxu,w,sx
2
1
2
2
]),,
ˆ
(2
)
ˆ
()
ˆ
([
4
1
1-kk1-k
1-k
iw,
1-kk1-k
L
i
1-k
iw,
1-kk1-k
f
ff
w
uwx
u,sw,xu,sw,x
(7)
Now, before calculating the measurement update,
covariance square-root column vectors for
measurement-update must be calculated.
i
ix,
1-k
k
x
Ps
i = 1, 2, … , L
(8)
i
k
iv,
1-k
Rs
i = 1, 2, … , L
v
(9)
Measurement update equations are calculated as
follows
),
ˆ
(h
LL
ˆ
kk
x
-
k
vxz
2
v
2
][
2
1
1
2
)
ˆ
(h)
ˆ
(h
k
ix,
kk
L
i
k
ix,
kk
x
v,sxv,sx
][
2
1
1
2
)
ˆ
(h)
ˆ
(h
iv,
kkk
L
i
iv,
kkk
v
sv,xsv,x
(10)
2
1
2
y
][
4
1
k
)
ˆ
(h)
ˆ
(h
k
ix,
k
-
k
L
i
k
ix,
k
-
k
-
ˆ
x
v,sxv,sxP
2
1
2
][
4
1
)
ˆ
(h)
ˆ
(h
iv,
kk
-
k
L
i
iv,
kk
-
k
v
sv,xsv,x
2
1
2
2
]2[
4
1
),
ˆ
(h)
ˆ
(h)
ˆ
(h
kkk
ix,
kk
L
i
k
ix,
kk
x
vxv,sxv,sx
2
1
2
2
]2[
4
1
),
ˆ
(h)
ˆ
(h)
ˆ
(h
kk
ix,
kkk
L
i
ix,
kkk
v
vxsv,xsv,x
(11)
T
k
ix,
k
-
k
L
i
k
ix,
k
-
k
i,x
k
)
ˆ
(h)
ˆ
(h
x
][
4
1
1
2
yx
kk
v,sxv,sxsP
(12)
1
yyx
kkk
ˆ
k
PPK
(13)
)(
kkkkk
ˆˆˆ
yyKxx
(14)
T
k
ˆ
k
KPKPP
kkk
yxx
(15)
Parameters are the scalar central difference interval
size. For Gaussian x, the optimal value is Lx, Lw,
and Lv are the dimensions of the state, process noise
and observation noise respectively. Q
k
is the
covariance matrix of motion noise and R
k
is the
covariance matrix of the observation noise. (.)
2
is the
shorthand for the vector outer product, i.e. a
2
= a.a,
and is the ith column of the matrix square root of the
square-symmetric matrix P (Norgard et al, 2000).
4 SIMULATIONS AND RESULTS
4.1 Evolution of the Map
The range bearing sensor mounted on the robot
returns the distance between the sensor and the
landmark as well as the angle between the robot’s
frame of reference and the landmark’s frame of
reference. Since all landmarks are considered static
in the environment, the reference frame of
landmarks is the same as global frame of reference.
The measurement information related to a landmark
is in form of polar measurement (D, β), indicating
]E[
kk
ww
])-)(-E[(
k
T
kkkkk
wwwwQ
]E[
kk
vv
])-)(-E[(
k
T
kkkkk
vvvvR
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
268

range and bearing angle of the landmark. In the
global frame of reference, the landmark coordinate
is referred by (x, y). In a standard filter (such as
EKF) the first order Taylor series truncation is used
to linearize this nonlinear observation model by
which the calculation of any possible error becomes
significantly inaccurate.
4.2 Robustness
As depicted in figure 1, the landmark position
located at (x=50.2 , y=149.8) is estimated by
incorporating range and bearing data (D, β) received
by the range/bearing sensor. In this case, zero-mean
Gaussian noise is added and the data is converted to
the Cartesian plane. As a result of low accuracy in
estimation of the bearing direction, samples appear
in form of banana shapes. As shown in figures 1-a,
1-b, and 1-c, the estimated mean and covariance of
this distribution is relatively far from the true mean
and covariance of the system. The estimation of the
mean and covariance in the UHS algorithm is shown
in figure 1-d which appears as the most accurate
estimation among all filters. The inaccuracy in
estimation of the mean in the range and the
covariance in FastSLAM algorithm, usually results
in the over estimation of the posterior distribution in
the range which leads the filter to become over
confident. HybridSLAM would produce an
inaccurate mean and covariance since the
linearization is based on the first order of Taylor
series (Julier et al., 2001). As long as the map has a
small size, all filters tend to approximate the mean
and covariance of the system reasonably.
Once the track becomes large, EKF fails to
estimate an accurate map and both FastSLAM and
HS become overconfident. Unlike the other three
filters, UHS performs with minimum error in the
mean and the covariance estimate which indicates
high accuracy and the robustness of the filter.
4.3 Map Fusion
In order to demonstrate how the map is evolved in
the estimation process, a scenario is simulated in this
section. Figure 2 illustrates an environment with a
few landmarks gathered in small groups. The vehicle
velocity is set on 2 m/s and the range for the
range/bearing laser is 10 meters. As the vehicle
starts localizing from point (0, 0), two landmarks at
locations (x=2.3,y=5.2) and (x=5.0,y=3.6) are
observed by the range finder. These landmarks are
the first features observed in the vicinity of the
vehicle, building the first piece of the map using
(a)
(b)
(c)
(d)
Figure 1: Estimation of the mean and covariance of a
landmark a) EKF-SLAM b) FastSLAM c) HybridSLAM
d) Unscented HybridSLAM.
49.5 50 50.5 51
149.5
149.6
149.7
149.8
149.9
150
150.1
EKF-SLAM
x direction (m)
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
y direction (m)
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
49.5 50 50.5 51
149.5
149.6
149.7
149.8
149.9
150
150.1
FastSLAM
x direction (m)
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
× ×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
× ×
×
×
× ×
×
×
×
y direction (m)
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
49.5 50 50.5 51
149.5
149.6
149.7
149.8
149.9
150
150.1
HybridSLAM
x direction (m)
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× ×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
y direction (m)
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
49.5 50 50.5 51
149.5
149.6
149.7
149.8
149.9
150
150.1
Unscented HybridSLAM
x direction
(
m
)
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
y direction (m)
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
HybridSLAM:ARobustAlgorithmforSimultaneousLocalizationandMapping
269
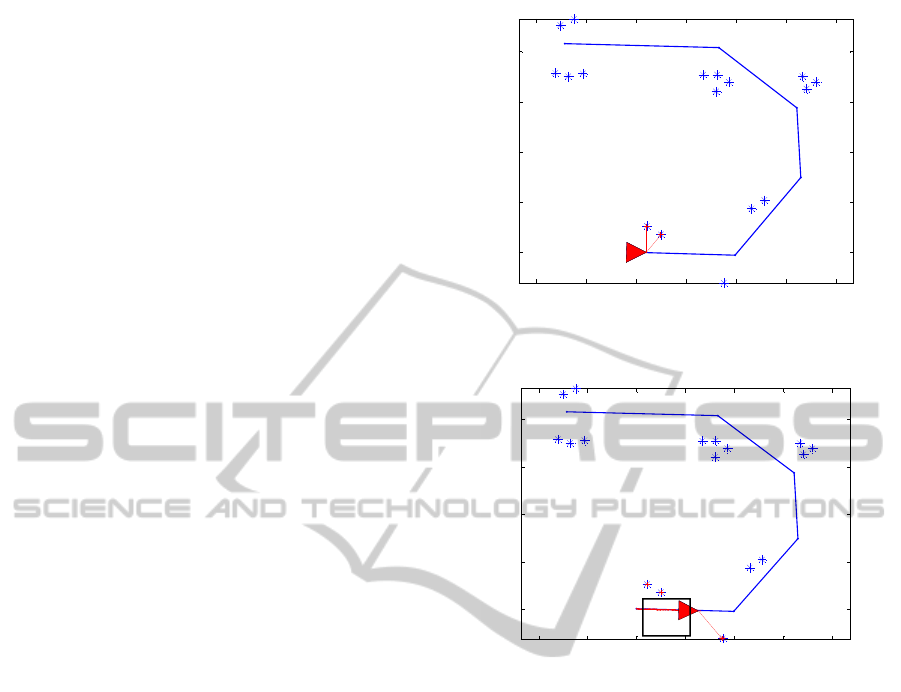
subordinate filter FastSLAM. At the same time,
UKF is building the same map independently. Once
the first piece of the map is estimated by both filters,
the map built by FastSLAM will be added to the
global map and at the same time, the uncertainty
difference between sub-filter estimations will be
taken into account. Once the robot observes first set
of landmarks in the vicinity, the first region is added
to the global map. The Constraint Local Sub-map
Filter (CLSF) constraint [7] would compare the map
estimated by the particle filter to a map produced by
UKF. This is the very important stage to choose one
map estimated over the other one. Depending on
how accurate the map is constructed, a final decision
is made and the first local map is added to the global
map. In figure 3 the region added to the map is
shown by a rectangle and the new region is under
observation. Robot is approximately at the
coordinate (10, 0). The first region inside the square
is already a part of the global map. The robot is
observing the second region consisting of only one
landmark. Same as the first region, the map of the
new region is built by both subordinate filters and
through CLSF the decision is made to add the most
updated and accurate map to the global map.
Once the second region in the vicinity of the
robot is estimated, it is also evaluated by CLSF
which has already included the map by UKF. The
decision is now based on the CLSF algorithm
evaluation to compare the two maps built by
different filters. If the map built by UKF is not
crossing its threshold, it remains as is. If CLSF
figures out that the map built by FastSLAM is more
accurate relative to the one built by UKF, the
accurate map is used. Figure 4 demonstrates the new
area surrounded by a plaque and added to the global
map. The first and second regions of the map are
identified and part of the global map. The robot
starts observing the third region from point (23, 3)
with respect to the global map. The first and second
regions are now correlated and have a critical role
for the next decision making by CLSF. It should be
noted that at this point, the first region is correlated
with the second region and as a whole map, regions
are expecting for the third region to be added to the
map in order to complete the map up to that time
step. In Unscented HybridSLAM algorithm, the
local mapping is occurring and at the same time the
map built by UKF is supporting the whole mapping
process (Julier and Uhlmann, 2004).
Usually in the EKF-SLAM sub-algorithm of HS,
spurious observations are associated with landmarks,
particularly during transient periods of high vehicle
uncertainty. It should be noted that the Failures as
Figure 2: Robot at coordinate (0,0).
Figure 3: Robot is approximately at the coordinate (10, 0).
the result of the EKF filter in HS does not happen in
the proposed algorithm in similar scenarios. Even
though the landmark is not observed simultaneously,
the ambiguity can be resolved. The local
linearization error is another failure mode of EKF-
SLAM which is not occurring when it is replaced by
UKF. When the UKF algorithm begins to build a
local map, the linearization error is at its minimum
level. As a result, the uncertainty becomes small. In
such case where the local-map uncertainty can be
significant, the robustness of the UHS would cover
any possible fault by integrating spurious
observations of data association information of the
observed landmark over time (Bailey et al, 2006). In
figure 5 the correlation of three identified regions of
the map is shown. The robot is approximately at
point (33, 26) and observing the fourth region in the
vicinity. Same process will follow to add a new
piece to the map. The third region is indicated by a
trapezoid and contains two individual landmarks.
-20 -10 0 10 20 30 40
0
10
20
30
40
Map Evolution (UHS)
x direction (m)
y direction (m)
-20 -10 0 10 20 30 40
0
10
20
30
40
Map Evolution (UHS)-First region is covered
x direction
(
m
)
y direction (m)
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
270
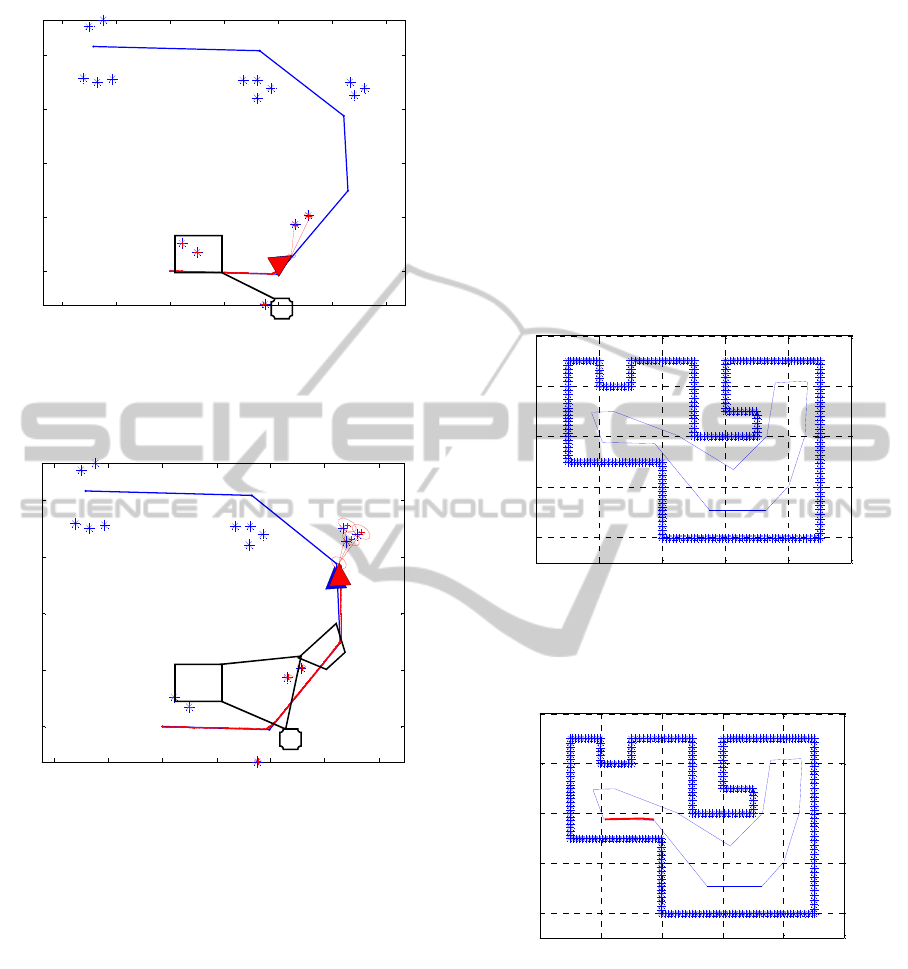
Figure 4: Robot starts observing the third region from
point (23, 3) with respect to the global map.
t
Figure 5: Robot is approximately at point (33, 26) and
observing the fourth region in the vicinity.
4.4 Map Update
Figure 6 demonstrates a loop closing scenario in a
domestic environment utilizing edges as line
segments. The environment is a 50m by 50m area
and the starting point is set on the global
coordination (x=11,y=29). Edges are composed of
approximately 1.00m distant landmarks by which
lines at the corners of the environment are
represented. In this simulation, map update process
is demonstrated through sequential figures. The
sensor installed on the robot returns the range and
bearing information to landmarks in the
environment. The sensor range for this simulation is
set to 20 meters and vehicle speed is set to 2 m/s. As
shown in figure 6, the robot arrives at waypoint 2,
estimating and updating the map of the environment.
Black dots around landmarks indicate estimated
locations of landmarks that are not incorporated into
the map fusion process. At some point, the location
of a particular landmark is over-estimated either by
the FastSLAM sub-filter or by the UKF sub-filter. In
this case, CLSF decides not to fuse that information
into the global map and instead, updates the map
with the previous data. On the other hand, if the
estimation is not beyond some threshold, location of
a landmark is fused to the global map, and as a
result, becomes part of the absolute map that the
system can rely on for the next time steps.
Figure 5: True map of a 50m by 50m environment in
which waypoints are set. Waypoints are connected by
straight lines showing an imaginary path.
Figure 6: Robot is at the second waypoint.
In figure 7, the robot is arrived at the sixth waypoint.
More landmarks at the range of the sensor are
observed and the map is still built using both
suboptimal filters and with a final supervision of
CLSF. As the process goes on, landmarks that have
been observed in previous time steps are re-observed
from the new robot locations, and help the system to
ignore previous wrong estimations. Black “dots” and
red “crosses” in this picture are changing their
locations as the process proceeds. Figures 8 and 9
-20 -10 0 10 20 30 40
0
10
20
30
40
Map Evolution (UHS)-Second region is covered
x direction
(
m
)
y direction (m)
-20 -10 0 10 20 30 40
0
10
20
30
40
Map Evolution (UHS)-Third region is covered
x direction (m)
y direction (m)
0 10 20 30 40 50
10
20
30
40
50
True Map of the Environment and Waypoints
x direction (m)
y direction (m)
O
O
O
O
O
O
O
O
O
O
O
O
O
0 10 20 30 40 50
10
20
30
40
50
Reaching the Second Waypoint
x direction (m)
y direction (m)
O
O
O
O
O
O
O
O
O
O
O
O
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
× × ×
×
×
× ×
×
×
×
×
×
× ×
×
×
×
×
×
× × ×
×
×
×
×
×
×
× × ×
×
×
×
× ×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
× × ×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
× × × × ×
× ×
×
× ×
× × ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× ×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
.
×
×
×
×
×
×
×
×
×
× ×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× × ×
×
×
× ×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
× ×
×
× ×
×
× ×
× ×
× ×
×
×
×
×
× × ×
× ×
× × ×
×
×
×
× ×
×
×
×
×
× ×
× ×
×
×
× ×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
× ×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
O
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
. . .
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. . .
.
. .
.
.
. . .
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
.
. .
.
.
.
.
. .
.
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . . .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
.
. .
.
. .
.
.
.
.
.
.
.
.
.
.
. .
.
. .
. .
.
. .
.
.
.
. . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
. .
.
. .
.
. .
.
.
.
.
.
.
.
.
.
.
. .
.
. .
. .
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
. .
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
. .
.
.
.
. .
. .
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
HybridSLAM:ARobustAlgorithmforSimultaneousLocalizationandMapping
271
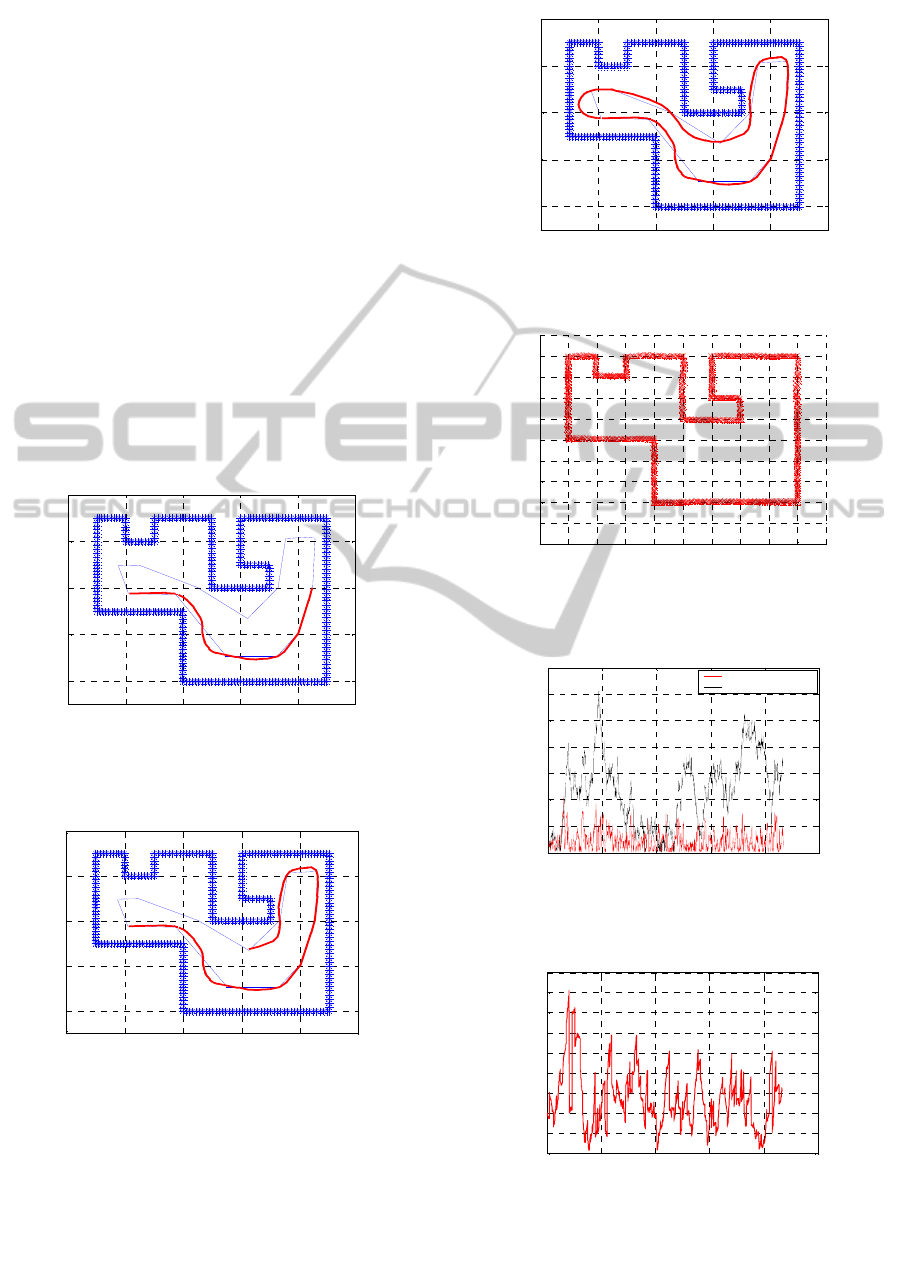
illustrate the resulting map at the tenth waypoint and
at the end of the loop closing. Figure 10
demonstrates the final version of the map built
during the loop closing indicating that the map
update process has been successful using UHS. This
map is now considered as the basis for global map
referenced for the next cycle. Figures 11 and 12
show the RMS position and orientation error
regarding the scenario depicted in figure 9. For this
simulation, 300 particles are used and the vehicle
velocity is set to 1.5m/s. RMS position error remains
around 0.35m in average and the orientation error, in
average is around 0.02 radians. The UHS algorithm
appears to perform with a high accuracy in this case.
Once the loop is closed, the map produced at the
end of the loop will be used as a referenced map
(global) for the next loop. It is very important to
mention that at the beginning of the second loop, the
SLAM problem may be treated as just a localization
problem.
Figure 7: Sixth waypoint is reached by the robot and the
map is built by suboptimal filters and the CLSF.
Figure 8: Robot is at the tenth waypoint.
Figures 13 and 14 depict the 2-sigma standard
deviation (95%) vs. the innovation in terms of
vehicle heading angle as well as its distance.
Simulations show that the mean remains close to
zero which results in a reliable and consistent map
Figure 9: End of the first loop.
Figure 10: Map of the environment is built prior to the
next loop.
Figure 11: Orientation error is 0.02 radians in average for
the SLAM process using UHS.
Figure 12: RMS position error is 0.35m in average for the
SLAM process using UHS.
0 10 20 30 40 50
10
20
30
40
50
Reaching the Sixth Waypoint
x direction (m)
y direction (m)
O
O
O
O
O
O
O
O
O
O
O
O
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
× × ×
×
×
× ×
×
×
×
×
×
× ×
×
×
×
×
×
× × ×
×
×
×
×
×
×
× × ×
×
×
×
× ×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
× × ×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
× × × × ×
× ×
×
× ×
× × ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× ×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
.
×
×
×
×
×
×
×
×
×
× ×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× × ×
×
×
× ×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
× ×
×
× ×
×
× ×
× ×
× ×
×
×
×
×
× × ×
× ×
× × ×
×
×
×
× ×
×
×
×
×
× ×
× ×
×
×
× ×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
× ×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
O
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
. . .
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. . .
.
. .
.
.
. . .
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
.
. .
.
.
.
.
. .
.
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . . .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
.
. .
.
. .
.
.
.
.
.
.
.
.
.
.
. .
.
. .
. .
.
. .
.
.
.
. . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
. .
.
.
.
.
.
.
.
. . .
.
.
.
.
.
.
. .
.
.
.
. .
. .
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
×
.
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
× ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
× ×
×
× ×
× ×
×
× ×
×
× ×
×
×
×
×
×
×
×
× ×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× × ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
× ×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
× ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
× ×
×
×
×
×
× ×
×
× ×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
. .
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
. . .
.
.
.
.
.
. .
.
.
.
.
. .
.
. . . .
.
.
. .
.
.
. .
.
.
.
.
. .
.
.
.
. .
.
.
. .
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
. . .
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
.
.
.
.
.
. .
. .
. . .
.
. .
.
.
.
.
.
. . .
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
. . .
.
.
. .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
. . .
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
.
×
×
×
×
×
×
×
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
. .
. .
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
. . .
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
. .
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
. . .
.
. .
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . .
.
.
.
.
.
.
.
.
.
. .
.
. .
.
. .
.
.
.
.
.
. .
.
.
.
.
.
.
.
. .
.
.
.
.
. . .
.
0 10 20 30 40 50
10
20
30
40
50
Reaching the Tenth Waypoint
x direction (m)
y direction (m)
O
O
O
O
O
O
O
O
O
O
O
O
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
× × ×
×
×
× ×
×
×
×
×
×
× ×
×
×
×
×
×
× × ×
×
×
×
×
×
×
× × ×
×
×
×
× ×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
× × ×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
× × × × ×
× ×
×
× ×
× × ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× ×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
.
×
×
×
×
×
×
×
×
×
× ×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× × ×
×
×
× ×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
× ×
×
× ×
×
× ×
× ×
× ×
×
×
×
×
× × ×
× ×
× × ×
×
×
×
× ×
×
×
×
×
× ×
× ×
×
×
× ×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
× ×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
O
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
. . .
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. . .
.
. .
.
.
. . .
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
.
. .
.
.
.
.
. .
.
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . . .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
.
. .
.
. .
.
.
.
.
.
.
.
.
.
.
. .
.
. .
. .
.
. .
.
.
.
. . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
. .
.
.
.
.
.
.
.
. . .
.
.
.
.
.
.
. .
.
.
.
. .
. .
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
×
.
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
× ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
× ×
×
× ×
× ×
×
× ×
×
× ×
×
×
×
×
×
×
×
× ×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× × ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
× ×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
× ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
× ×
×
×
×
×
× ×
×
× ×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
. .
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
. . .
.
.
.
.
.
. .
.
.
.
.
. .
.
. . . .
.
.
. .
.
.
. .
.
.
.
.
. .
.
.
.
. .
.
.
. .
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
. . .
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
.
.
.
.
.
. .
. .
. . .
.
. .
.
.
.
.
.
. . .
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
. . .
.
.
. .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
. . .
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
.
×
×
×
×
×
×
×
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
. .
. .
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
. . .
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
. .
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
. . .
.
. .
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
. .
.
.
.
.
.
. .
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
× × × × ×
×
×
×
×
×
×
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
. .
.
.
.
.
.
. .
.
. .
. .
. .
.
.
.
.
0 10 20 30 40 50
10
20
30
40
50
End of the Loop
x direction (m)
y direction (m)
O
O
O
O
O
O
O
O
O
O
O
O
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
× × ×
×
×
× ×
×
×
×
×
×
× ×
×
×
×
×
×
× × ×
×
×
×
×
×
×
× × ×
×
×
×
× ×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
× × ×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
× × × × ×
× ×
×
× ×
× × ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× ×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
.
×
×
×
×
×
×
×
×
×
× ×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× × ×
×
×
× ×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
× ×
×
× ×
×
× ×
× ×
× ×
×
×
×
×
× × ×
× ×
× × ×
×
×
×
× ×
×
×
×
×
× ×
× ×
×
×
× ×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
× ×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
O
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . .
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. . .
.
. .
.
.
. . .
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
.
. .
.
.
.
.
. .
.
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . . .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
.
. .
.
. .
.
.
.
.
.
.
.
.
.
.
. .
.
. .
. .
.
. .
.
.
.
. . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
. .
.
.
.
.
.
.
.
. . .
.
.
.
.
.
.
. .
.
.
.
. .
. .
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
×
.
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
× ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
× ×
×
× ×
× ×
×
× ×
×
× ×
×
×
×
×
×
×
×
× ×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
× × ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
× ×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
× ×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
× ×
×
×
×
×
× ×
×
× ×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
. .
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
. . .
.
.
.
.
.
. .
.
.
.
.
. .
.
. . . .
.
.
. .
.
.
.
.
.
.
.
.
. .
.
.
.
. .
.
.
. .
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
. . .
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
.
.
.
.
.
. .
. .
. . .
.
. .
.
.
.
.
.
. . .
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
. . .
.
.
. .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
. . .
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
.
×
×
×
×
×
×
×
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
. .
. .
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
. . .
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
. .
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
. . .
.
. .
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
. .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
. .
.
.
.
.
.
. .
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
×
×
×
×
×
×
× × × × ×
×
×
×
×
×
×
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
. .
.
.
.
.
.
. .
.
. .
. .
. .
.
.
.
×
×
×
× × ×
×
×
× × ×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
× ×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× ×
×
×
× ×
× × ×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
.
.
.
.
.
.
.
.
.
.
. .
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
. . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
. .
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
. .
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
. .
.
.
. . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
.
.
.
.
. .
.
.
.
.
.
. .
. .
.
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
. . .
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 5 10 15 20 25 30 35 40 45 50
0
5
10
15
20
25
30
35
40
45
50
x direction (m)
y direction (m)
Map of the Environment
0 200 400 600 800 1000
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
UHS Performance with 300 Particles
Time (s)
Orientation Error (radians)
Estimation Error
Dead Reckoning
0 200 400 600 800 1000
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
UHS Performance with 300 Particles
Time (s)
RMS Positon Error (m)
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
272
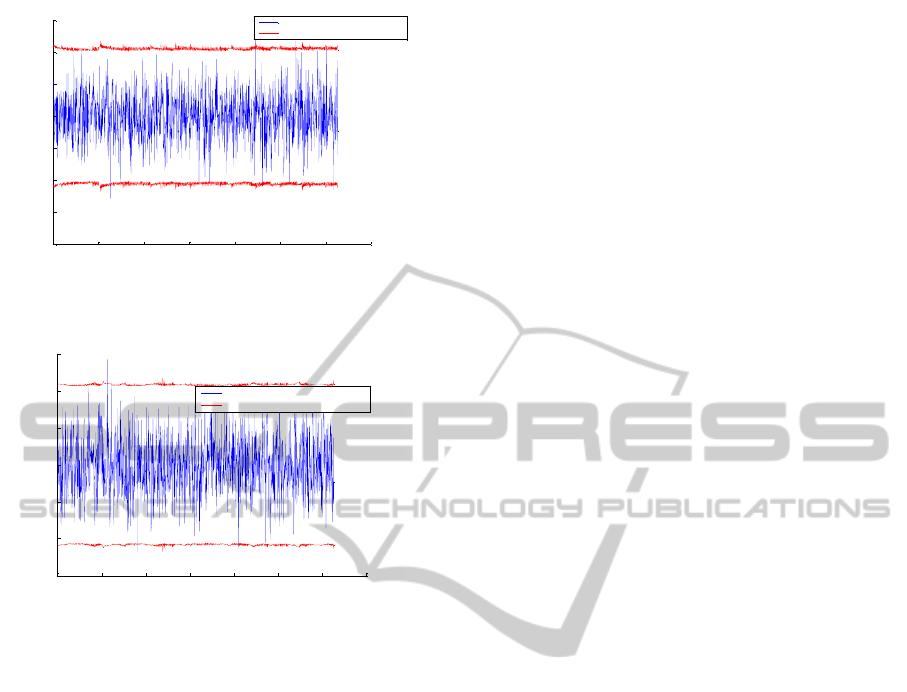
Figure 13: Standard deviation vs. distance innovation.
Figure 14: Standard deviation vs. angle innovation.
even though the loop is completed. Results show, as
long as the ambiguity of data association is reduced
by the UHS, a compact map configuration does not
affect the performance of the filter, and the results
would be identical to a SLAM case with a regular
loop closing case. This is important since filters such
as EKF fail to fulfill the navigation task in such
circumstances.
5 CONCLUSIONS
The main contribution of this study is a thorough
investigation and the validity check of Unscented
HybridSLAM. Simulations of the vehicle trajectory
and the estimation accuracy are investigated based
on proposed algorithm. The map accuracy and path
estimation are compared to currently used
algorithms, in particular, resulting in high quality of
the produced map and reducing error in estimated
position and robot heading. Results from different
scenarios indicate that the proposed algorithm is be
able to handle hundreds of nearby landmarks with
minimum data association ambiguity and a high
level of accuracy in the path estimation when
compared to currently used algorithms.
ACKNOWLEDGEMENTS
An academic version of a free software for robotics
research was used in this study. The software in
form of both MATLAB and C++ codes is available
at http://www.lasmea.univ-bpclermont.fr/ftp/pub/
trassou/SLAM/SLAM_Summer_School2002/SLAM
%20Summer%20School%202002.htm
REFERENCES
Smith R., Cheeseman P., 1986, The estimation and
representation of spatial uncertainty, International
Journal of Robotics Research, Vol. 5, Issue 4, pp. 56-
68.
Durrant-Whyte H., Bailey T., 2006, Simultaneous
localization and mapping (SLAM): part I the essential
algorithms, IEEE Robatics and Automation Magazine,
Vol. 13, No. 2, pp. 99-108, June.
Monjazeb A., Sasiadek J. Z., Necsulescu D., 2012, An
approach to autonomous navigation based on
Unscented HybridSLAM, Proc. of 17th International
Conference on Methods and Models in Automation
and Robotics, pp. 369-374, Miedzyzdroje, Poland.
Montemerlo M., Thrun S., 2003, Simultaneous
localization and mapping with unknown data
association using FastSLAM, Proceedings of the IEEE
International Conference on Robotics and Automation,
pp. 1985-1991, Vol. 2, September.
Bailey T., Mobile robot localization and mapping in
extensive outdoor environments, 2002, PhD Thesis,
Australian Centre for Field Robotics, University of
Sydney, Sydney, Australia.
Brooks A., Bailey T., 2009, HybridSLAM: Combining
FastSLAM and EKF-SLAM for reliable mapping,
Springer Tracts in Advanced Robotics, Volume 57,
pp. 647-661.
Williams S. B., Dissanayake G., Durrant-Whyte H., 2002,
An Efficient Approach to the Simultaneous
Localisation and Mapping Problem, Proceedings of
the IEEE International Conference on Robotics &
Automation, Washington DC.
Monjazeb A., Sasiadek J. Z., Necsulescu D., 2014,
Navigation of an Autonomous Mobile Robot Using
Data Association Method, Proc. of 11th International
Conference on Informatics in Control, Automation and
Robotics (ICINCO), pp. 304 - 311, Vienna, Austria.
Monjazeb A., Sasiadek J. Z., Necsulescu D., 2011,
Autonomous navigation among large number of
nearby landmarks using FastSLAM and EKF-SLAM; a
comparative study, Proc. of 16th International
Conference on Methods and Models in Automation
0 550 1100 1650 2200 2750 3300 3850
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
Distance Innovations
Time (s)
Deviation (m)
Innovations
Standard Deviation (95%)
0 550 1100 1650 2200 2750 3300 3850
-0.045
-0.030
-0.015
0
0.015
0.030
0.045
Angle Innovations
Time (s)
Angle Innovation (radians)
Inno vations
Standard Devication (95%)
HybridSLAM:ARobustAlgorithmforSimultaneousLocalizationandMapping
273

and Robotics (MMAR), pp. 369-374, Miedzyzdroje,
Poland.
Norgard M., Poulsen N., Ravn O., 2000, New development
in state estimation for nonlinear systems, IFAC
Automatica, pp. 1627-1638, Vol. 36, No. 11,
November.
Julier S. J., Uhlmann J. K., 2001, A counter example to the
theory of simultaneous localization and map building,
Proc. of IEEE International Conference on Robotics
and Automation, pp. 4238-4243, March.
Julier S. J., Uhlmann J. K., 2004, Unscented filtering and
nonlinear estimation, Proc. of IEEE Journal, Vol. 92,
Issue 3, pp. 401-422, March.
Bailey T., Nieto J., Nebot E., 2006, Consistency of
FastSLAM algorithm, Proceedings of IEEE
International Conference on Digital Object Identifier,
pp. 424-429.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
274
