
Calibration of Laser Range Finders
for Mobile Robot Localization in ITER
Tiago Sousa
1
, Alberto Vale
2
and Rodrigo Ventura
3
1
Instituto Superior Técnico, Universidade de Lisboa, Av. Rovisco Pais 1, 1049-001, Lisboa, Portugal
2
Instituto de Plasmas e Fusão Nuclear, Instituto Superior Técnico, Universidade de Lisboa,
Av. Rovisco Pais 1, 1049-001, Lisboa, Portugal
3
Laboratório de Robótica e Sistemas em Engenharia e Ciência, Instituto Superior Técnico, Universidade de Lisboa,
Av. Rovisco Pais 1, 1049-001, Lisboa, Portugal
Keywords:
Laser Range Finder, Calibration, Localization, ICP.
Abstract:
Remote maintenance operations in the experimental fusion reactor ITER may require vehicle localization, for
which one of the proposed methods is based on a network of Laser Range Finder sensor measurements. This
localization method requires an accurate knowledge of each sensor pose (position and orientation). A deviation
in sensor pose can compromise localization accuracy thereby recalibration procedure for the sensor poses is
often necessary. This paper studies several calibration algorithms based on ICP. Simulation and experimental
tests were carried out for different maps and situations regarding sensor pose uncertainty. The conclusion
proposes the best suited algorithms for each scenario.
1 INTRODUCTION
Producing enough energy to cover our civiliza-
tional primary energy needs and living standards, has
always been one of the main goals and focuses of our
modern civilization. The current growth in energy
supply demand has raised the concern on the environ-
mental impact of current ways of energy production
and lead to the discussion of reliable and new alter-
natives. Fusion power promises itself as a clean, and
sustainable source of usable energy. The biggest chal-
lenge now is to prove that a large scale functionality
and production is possible. The International Ther-
monuclear Experimental Reactor (ITER) is a multi-
national in-progress experimental project located in
Cadarache, south of France and represents the next
step of demonstration. Workers are not allowed to en-
ter the ITER facilities during its operation and trans-
portation of activated components (see Figure 1).
Instead, the nominal and maintenance operations
(A. Tesini, 2008) will be handled completely re-
motely. Some of the critical operations include the
transportation of shielded casks, that enclosures the
load and spare parts by the Cask and Plug Remote
Handling System (CPRHS) vehicles and Cask Trans-
port System (CTS) (Darren Locke, 2014) vehicles and
the operation of rescue vehicles such as the proposed
Multi Purpose Rescue Vehicle (MPRV) (J. Soares,
Figure 1: Problem illustration in ITER building.
2014) for inspection, repair and component replace-
ment. To perform the previous and other tasks with
minimal error margin, an accurate navigation method
is needed due to the tight safety margins inside the
building. The navigation uses the vehicles localiza-
tion estimation (J. Ferreira, 2013) to autonomously
maneuver the vehicle trough its path or to help a hu-
man operating it remotely. A network of Laser Range
Finder (LRF) sensors are proposed, due to their im-
munity to magnetic fields that proliferate in near the
Tokamak and high accuracy distance measurements
541
Sousa T., Vale A. and Ventura R..
Calibration of Laser Range Finders for Mobile Robot Localization in ITER.
DOI: 10.5220/0005536505410549
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 541-549
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
in long and short distances, which the localization es-
timation method is based and heavily reliant on.
Calibration is a problem that relies on most of the
sensors, in particular, the ones used in high demand-
ing accuracy applications. After the first calibration,
every sensor might need a recalibration depending on
some working condition factors such as level of tear,
stability and wear suffering during operational time.
Besides the general problems in calibration regard-
ing sensor’s own measurements, here the focus is on
calibrating the measurements between a network of
LRF sensors in such a way the measurements from
different sensors could have a valid correspondence
between them (see Figure 1). The devices are attached
to environment walls to reduce the chance of elec-
tronics being damage by the radiation. A deviation of
100 mm in sensor position and 5
◦
in orientation could
cause as much as a deviation of about 120 mm (as
stated in (J. Ferreira, 2013)) and 873 mm respectively
in vehicle location. These deviations compromise ma-
neuvers of hazard material transportation vehicles on
narrow and tight spaces.
LRF sensors have becoming of widespread use in
mobile robot systems because of its high accuracy
distance measurements. Among LRF, other sensors
such as cameras (IR and RGB) and odometry infor-
mation are often used simultaneously to guide au-
tonomous vehicles. Some methods for calibration be-
tween a camera and LRF have been proposed (Vin-
cenzo Caglioti, 2008), other methods such as SLAM
(Sebastian Thrun, 2008) use the odometry informa-
tion along LRF readings in its localization algorithm.
In the previous approach, after calibration, the results
are given in the robots frame which is not static, so the
readings might change with time. In ITER sensors are
fixed to environment walls. When calibration proce-
dure takes place, it is assumed that all measurements
are derived from the map so no fix or moving outliers
presence were considered. The only changes in LRF
consecutive measurements should be associated with
the sensor precision limits.
Some LRF calibration techniques have been
proposed such as (Antone and Friedman, 2007),
(K. Schenk, 2012) but all of them have one thing in
common: they require physical access to the environ-
ment where the calibration takes place. Since no hand
calibration is possible, the calibration procedure, like
many other operations in ITER context, must be made
entirely remotely. The Calibration techniques stated
before, use static or moving objects (or humans) that
must be asymmetrical to uniquely identify the target.
That is not the case as the CTS vehicle features a sym-
metrical rectangular shape and uses a rhombic-like
kinematics configuration for high maneuvering and
flexibility making heading extraction not trivial.
Given the physical access constraints of ITER, a
map description of the environment shall provide the
valuable opportunity to check and compare where the
LRF measurement data best fits on the map. There-
fore the map layout description should be as accurate
as possible to mitigate the impact of erroneous walls
dimensions or unmapped areas/objects on results.
This paper is divided as follows: Section 2
presents the proposed solution. The implemented
simulation environment is described in Section 4, pre-
ceded by the obtained results in Section 5. Finally, the
last section is reserved for the conclusions discussion.
2 PROBLEM STATEMENT
In ITER, the optimal locations where the LRF sensors
should be installed are determined beforehand by an
algorithm in (J. Ferreira, 2013). As a consequence
of sensor misplacement, measurements from distinct
LRF lose correspondence between them. Address and
solving this problem is the main focus and objective
of the present work. This issue, where the exact posi-
tion and orientation of the sensors are spoiled, can be
caused by human error on installation procedure, er-
roneous map measurements or any other factor such
as the ones mentioned in Section 1.
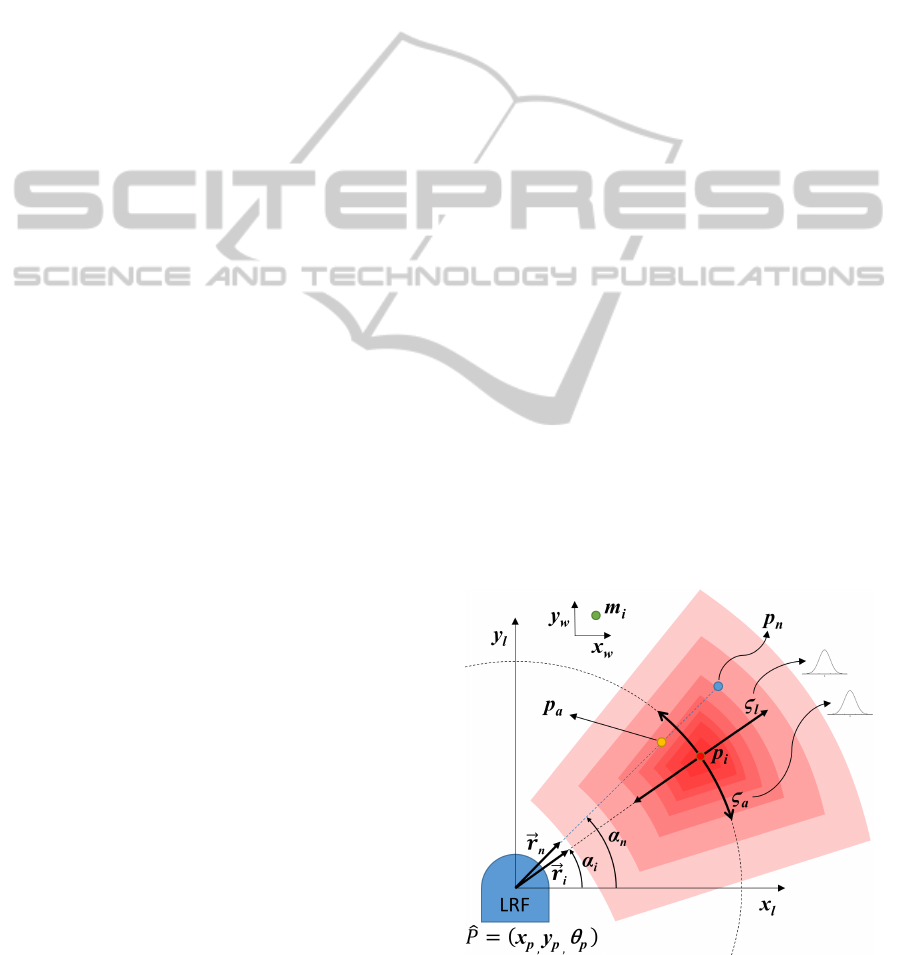
The pose P, for a given sensor in the network, in-
cludes its position coordinates (x
p
,y
p
) in meters and
its orientation θ
p
in angle degrees. Both are given
in the map coordinate frame (x
w
,y
w
) as illustrated in
Figure 2. Also a horizontal orientation is assumed
(pitch and tilt not influential).
Figure 2: Variables involved in the problem description.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
542

The LRF sensors return data in two dimensional polar
coordinate system where the distance measurements
k
r
n
k
and the associated angle α
i
are given in device
frame (x
l
,y
l
). Since the distance measurements are
affected by noise, LRF returns
k
r
n
k
measurements in-
stead of the true
k
r
i
k
yielding the p
n
points. The ob-
jective is to estimate the absolute final pose,
ˆ
P
f
, of
each sensor in the network that minimizes the mean
quadratic error, e
pp
, function in (1). The residual is
composed by the point to point Euclidean distance be-
tween the transformed LRF measurements T (
ˆ
P
f
, p
n
)
and the respective map closest points m
n
. This is a dif-
ficult optimization problem due to several local min-
ima existence.
e
pp
= argmin
ˆ
P
f
1
N
N
∑
n
kT (
ˆ
P
f
, p
n
) −m
n
k
2
(1)
3 PROPOSED SOLUTION
The proposed solution is a main algorithm that re-
ceives as input a map description, LRF measurement
data, and an optional initial pose estimate
ˆ
P
i
. The un-
certainty degree associated with this parameter leads
to four different scenarios (denoted A, B, C, and D
below) that specify the way the algorithm behave. In
case an initial pose estimate is given (scenario A), the
algorithm behaves locally trying to extract the best
pose for the given measurements. Instead, if an ini-
tial pose estimate is not given at all (scenario D), the
algorithm behaves globally on the map, assuming any
pose is plausible. Other two intermediate scenarios
(B, C) may occur whenever one parameter of the ini-
tial pose is missing.
3.1 Data Pre-processing
This first phase in the algorithm execution is common
in every case scenario. By averaging raw data from
multiple scans, it is possible to mitigate the errors in
readings derived from the random errors in LRF de-
vices. This way precision improves proportionally to
the square root of the number of complete scans as
stated in (Markus-Christian Amann, 2000). But be-
fore averaging, a normality test takes place to verify
if data its well a modeled normal distributed popu-
lation so an averaging metric could be meaningful in
this context. The averaging method implemented uses
a significant number of scans (at least one hundred) to
determine the average value µ, and the standard devia-
tion σ. Using a window interval, w, given by (2) it was
possible to reject the extreme values before applying
the average metric. As average metric is strongly in-
fluenced by extreme values, and after some experi-
mentation, only the values inside of σ range (68%)
were considered to reduce this negative effect.
w = [µ − σ,µ + σ] (2)
3.2 A: Initial Pose Known
In this case, an initial pose estimate (position and ori-
entation) is completely known, and, therefore, a local
based search is performed using LRF readings against
the map. In order to match the data type returned
from LRF readings (Cartesian points), the map line
segments need to be transformed into a significant
number of points to preserve data integrity as much as
possible. The origin of the LRF points are translated
to the given position coordinates and rotated accord-
ing to the given orientation. Then, a matching pro-
cedure takes place to adjust and align the LRF points
with the map points to determine the best fitting pose.
To match the two point clouds and evaluate the dis-
placement error, the Iterative Closest Point (Besl and
McKay, 1992) (ICP) algorithm, represented in (3),
was used.
R
k
,t
k
= argmin
R,t
1
N
N
∑
i
kRp
k
i
+t − m
k
i
k
2
(3)
The map points, m, are chosen as the reference and
LRF points, p, are subject to a rigid body transfor-
mations R,t that aligns the two by minimizing the
quadratic error of the point to point distance metric at
each k iteration for the all the N LRF points. The algo-
rithm stops when the point association between the k
and k −1 iterations are the same. The resultant output,
R
k
and t
k
, is the rigid body transformation that best
fits the two point clouds and is determined from SVD
decomposition (K. S. Arun, 1987). By applying the
result to the initial guess the final pose estimate is re-
vealed. One major drawback in this algorithm is that
the ICP can be trapped in local minima and this is the
main reason why it has been chosen for local search
scenario. Variations of this algorithm that matches
points to lines such as (Low, 2004)and (Censi, 2008),
have been proposed but the error metrics require non
linear minimization metrics which are solved using
approximations and are not robust against large initial
displacement error. Point to point metric presents a
closed form solution and converge faster despite time
not being a priority in the context of this application.
If the solution presents an associated error with a or-
der of magnitude higher than the devices standard de-
viation (STD), the initial pose estimate was not good
enough therefore other case scenarios are applied. In
these other scenarios where the initial pose estimate
is incomplete or non-existent, the resultant pose esti-
mate always suffer a final ICP alignment.
CalibrationofLaserRangeFindersforMobileRobotLocalizationinITER
543

3.3 B: Only Position Known
In this case only a position initial estimate is known.
Taking advantage of the available information, the
proposed solution consists in a brute force approach
of the previous scenario. Thus the ICP algorithm is
initialized for a predefined set of poses where only
the estimate orientation angles vary. The chosen ori-
entation values should be as low as possible apart so
the ICP algorithm has a higher chance to converge to
the optimum solution without being stuck in a local
minima. The final estimated pose is given by the pose
with the lowest ICP associated e
pp
.
3.4 C: Only Orientation Known
When only the orientation initial estimate is given,
again, a brute force version of ICP could be applied
varying the position, but depending on the point den-
sity of the map, the successive ICP could become very
computationally heavy. As an alternative, a novel
method was developed consisting in using the read-
ings as a projection of the possible location of the
sensor. Every single LRF measurement is projected
backwards from each map point revealing a LRF pos-
sible location. A vote is then accumulated for the re-
spective coordinates. The coordinates which have a
higher vote count determines the most likely position
estimate.
3.5 D: Initial Pose Unknown
This is the worst case scenario as the LRF location
can be anywhere in the map. In order to reduce the
search space, when compared to the previous solu-
tions, a different approach was taken. The method
presented does not taken into account the wall instal-
lation constrain and is divided into two phases: fea-
ture extraction and matching features. A flowchart
is provided on Figure 3, which depicts the following
different phases and main steps involved in this case
scenario.
Figure 3: Flowchart of scenario D.
3.5.1 Feature Extraction
The objective in this phase is to extract line segments
and vertex points from the processed LRF output data.
A comparison between some of the most common
line extraction methods is present in (Viet Nguyen,
2007). Based on the conclusions, the most correct and
best suited method for the localization problem with
an a priori map was the Split and Merge technique
preceded by a clustering algorithm. So the first step
is to perform a primary classification of points using
a clustering technique. The Distance based Convolu-
tion Clustering (DCC) proposed by (Carlos Fernán-
dez, 2010) was used. It consists on identifying break
points based on a sudden change of the distance be-
tween consecutive scan points, and once one is found
a new cluster is created. To do that, a high pass filter is
applied to the set of euclidean distances between con-
secutive points. The break points are identified where
the convolution is greater than a cluster threshold
whose value is proportional to the LRF readings stan-
dard deviation. Wrong or missing breakpoint identifi-
cation can happen as this is a simple and primary ap-
proach. The following step uses the Split and Merge
algorithm to confirm and correct for those erroneous
cases in order to finally extract lines and vertex points.
The Split and Merge technique begins by the splint-
ing phase where the objective is to create sub-clusters
of a cluster based on the evidence of a line pattern
points. A line fits the points using an ordinary least
squares line fitting technique and a breakpoint is iden-
tified if the most distant point to the line is greater than
a given split threshold. Since the previous procedures
can wrongly create more than one line segment for the
same correspondent line in the map, a merging phase
is conducted to unify similar clusters. If two neighbor
segments have its respective, angle difference inferior
to a given slope threshold, and distance between two
extreme points inferior to a proximity threshold, the
two respective clusters are unified. The segment line
parameters, for this unified cluster, are extracted, this
time, using a M estimator robust line regression tech-
nique with a bi-square weight function. Vertex points
are extracted extending and intercepting consecutive
and close enough line segment extremes.
3.5.2 Feature Matching
The matching phase takes advantage of the geometric
features extracted previously, specially the vertexes.
An extraction of map vertexes is first performed, and
then, a matching hypotheses is formed for every pair
combinations of map vertexes and extracted vertexes.
Assuming a vertex is the common extreme point of
two different line segments, after overlapping the two
vertex points in the pair by a translation transforma-
tion means, there exists a four possible pair combi-
nations of alignments for the vertexes respective line
segments. This alignments are done by means of rota-
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
544

tions. The extracted rigid body transformation is ap-
plied to all LRF points and after this transformation
the pp error function in (1) is used to assess and eval-
uate the displacement between the two point clouds.
The resultant estimated pose,
ˆ
P
f
, is determined from
the transformation that yields the lowest error. In case
no vertexes are extracted, threshold values that af-
fect the feature extraction phase are changed and the
procedure is repeated. If the combinations of tested
threshold values are not enough to produce a valid re-
sult, i.e., a result whose the point to point error value
is relatively close to the devices standard deviation, an
extremes matching method is applied. This method
procedure is similar to the vertex method except it
uses end points of extracted line segments instead of
vertexes. For every pair of points (one map vertex and
one end point from an extracted line) a two combina-
tion matching (instead of four) is done by aligning the
line segment with the two map lines that originate the
map vertex in question.
4 SIMULATED RESULTS
4.1 LRF Simulation
To test and confirm the proposed solution, a simulator
was developed which is composed by two parts: the
LRF model and LRF scan procedure. The two are in-
timately linked as the model contains the device prop-
erties that influence the scan result. Noise source, in
LRF devices, mostly comes from internal electronics
generating jitter, walk nonlinearity, and drift (Markus-
Christian Amann, 2000) which affect sensor accuracy
not only by distance reading means but angular steps
also suffer from deviation despite being almost in-
significant. To simulate noise, a normal distribution,
with zero mean and standard deviation given by man-
ufacturer, was chosen to model the deviation from the
correct value, p
i
. This point is obtained in the simu-
lator by intercepting every sensor ray with every wall
and selecting the appropriate point. The coordinates
of a point affected by noise, p
n
, is given by (4).
p
n
= T
v
(ζ
l
) ∗(p
a
(ζ
a
,~r
i
)) (4)
It should be noted that linear and angular noise are
not commutative operations due to the nonlinearity of
map. That being said, first, the p
a
is obtained from
provoking an angular deviation ζ
a
to ~r
i
yielding ~r
n
.
Then T
v
(ζ
l
) applies a linear deviation of ζ
l
in the di-
rection of ~r
n
(see Figure 2). A value for the LRF range
parameter is often given by the manufacturers under
certain ideal conditions and a range correction factor
is often provided to compensate for changes of these
conditions. For simulation purpose meteorologic con-
ditions are assumed fine with no influence on read-
ings. The target reflectivity coefficient indicates the
amount of energy it is capable to reflect. As far away a
target is, the higher the reflectivity necessary to a LRF
detect the reflected beam. This dependence character-
istic, often present in LRF manuals, was implemented
in the simulator to validate the readings. Walls shape
were considered diffuse so the target reflectivity value
seen by the LRF is corrected by a cosine of the in-
cidence angle factor. Due to the lack of informa-
tion inherent of a two dimensional map representa-
tion, neither color or target size influences were taken
into account in the simulation scan process. As for
resolution limits, linear resolution was implemented
rounding the distance value,
k
r
n
k
, to the level of un-
certainty of the LRF model, and angular resolution is
the value that determines the angle α
i
of each ray scan
line given the configurable field of view (FOV) value.
The output is composed by a set of
k
r
n
k
distance mea-
surements and the associated α
i
angles. Reflectivity
can also be returned for some models.
4.2 Results
To evaluate the algorithm performance, tests were
performed in simulation environment. Due to the na-
ture of simulation, the true pose is available to com-
pare against the results. Four tests were performed for
each map, each of the tests for different scenarios as
described in Section 3. Two maps, converted to points
with a density of 50 points per meter, with no outliers
in both, were used. The first one is a simple created
asymmetrical map and the other a complex map from
ITER basement, where the actual CPRHS will navi-
gate, represented respectively from left to right in Fig-
ure 4.
Figure 4: LRF sensor used in simulation testing scenarios.
For each a model of a LRF was created featuring
the following main properties: 180
◦
of FOV, STD of
±50 mm, maximum range of 100 m, linear resolution
of 1 mm and angular resolution of 0.5
◦
. Each LRF
CalibrationofLaserRangeFindersforMobileRobotLocalizationinITER
545
were set in the predefined poses represented in Figure
4, from where only one scan was taken. In scenario D,
the tolerance values that gave the best results, for the
clustering and feature extraction were the following:
0.5 m for proximity, 5
◦
for slope, 1 m for clustering
and 0.5 m for split.
The results obtained for the simple asymmetrical
map and for ITER map are presented in table 1.
ˆ
P
t
in-
dicates the exact true pose where the measures were
taken from,
ˆ
P
i
is an initial guess, at least, 1 meter
away from the true position,
ˆ
P
f
is the final pose re-
sulting from the algorithm output, “pp err.” is the
point to point error given by (1), “abs. error” is the
difference between true pose and final pose and “RT”
(run time) is the time elapsed in the algorithm execu-
tion
1
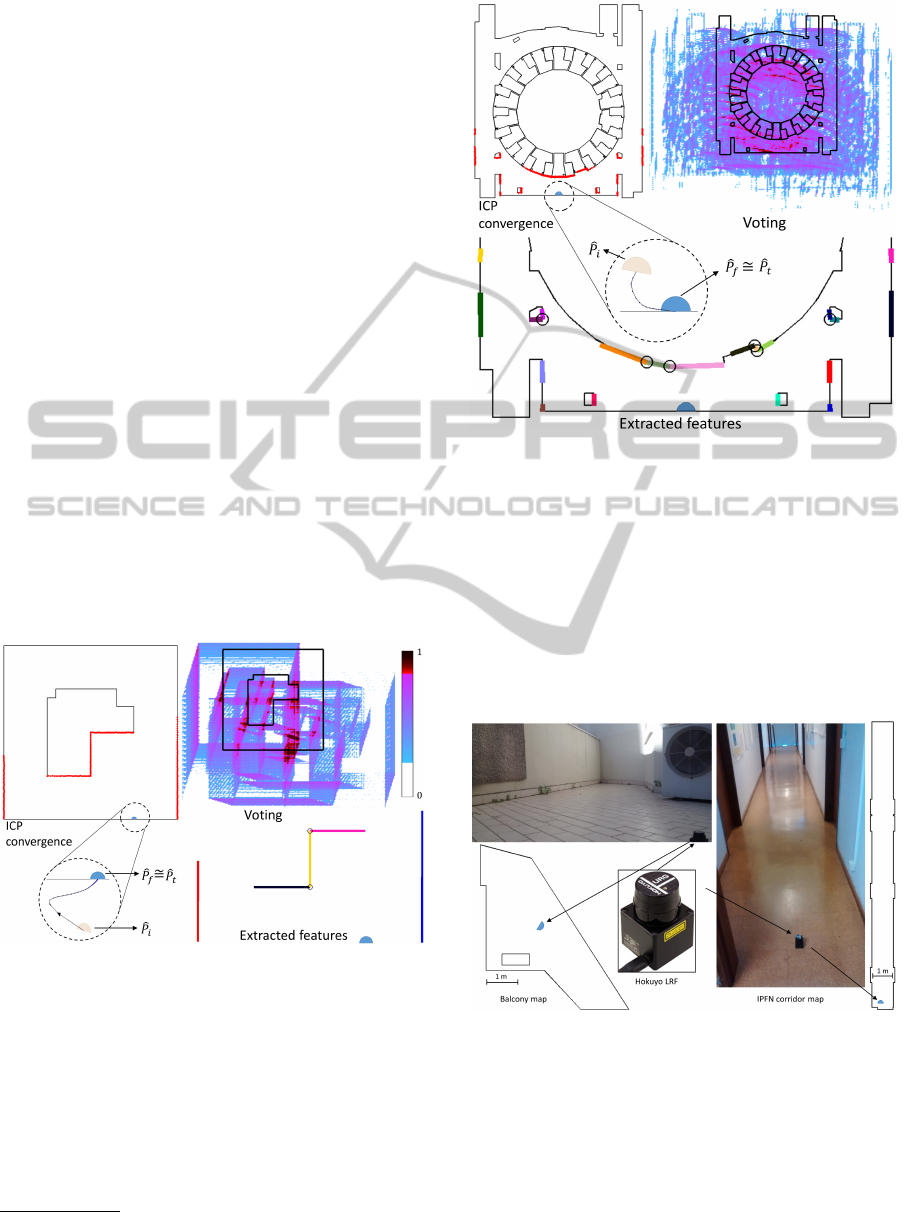
. Images of the results are displayed respectively
in Figures 5 and 6. In each figure three images are
displayed: at the left side the ICP resultant alignment
of LRF points (in red) and the respective iterative evo-
lution from
ˆ
P
i
to
ˆ
P
f
, the heat map resulting from the
voting method is shown on the upper right section,
and on the lower section the geometrical features ex-
tracted (vertexes represented by the small circles) in
the vertex method are pictured. For scenario B an ar-
ray of 13 different and equally spaced angle values
were used and the result is not displayed because it is
similar to the ICP result.
Figure 5: Simulation results for asymmetrical map.
5 FIELD RESULTS
5.1 Sensors Specification
The LRF device used was a Hokuyo URG-04LX-
UG01 (see Figure 7). The following main specifica-
tions were taken from the respective device manual:
1
tests were always done on the same machine, an i5 proces-
sor.
Figure 6: Simulation results for ITER map.
240
◦
of FOV, STD of ±50 mm, maximum range of 4
m, linear resolution of 1 mm and angular resolution of
0.36
◦
. The LRF sensor was set in a predefined mea-
sured position and orientation shown in Figure 7. At
least, data from one hundred scans were gathered and
processed to reject discrepant value measurements. In
scenario D, the tolerance values that gave the best re-
sults, for the clustering and feature extraction were
the following: 0.1 m for proximity, 15
◦
for slope, 0.1
m for clustering and 50 mm for split.
Figure 7: LRF sensor, photos and maps used in experimen-
tal testing.
5.2 Field Tests
Two distinct maps were used in the field test as well,
one from a house balcony which contain some out-
liers, and the other from an office corridor (Figure
7) composing a common environment of doors and
long walls. Both maps were converted to points with
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
546

Table 1: Experimental results table.
Simulated Scenarios
Map Scen.
ˆ
P
t
[m, m,
◦
]
ˆ
P
i
[m, m,
◦
]
ˆ
P
f
[m, m,
◦
] pp err. [mm] Abs. err. [mm,
◦
] RT[s]
Asymm.
A
(75.000, 0.000, 90.0)
(73.550,-5.280,73.0) (75.004, 0.002, 90.0) 53.1 (4.1, 0.0) 4.2
B (73.550, -5.280, -) (75.008, 0.007, 90.0) 53.1 (10.4, 0.0) 59
C (-, -, 73.0) (65.752, 0.852, 73.0) 4050.3 (9286.9, 17.0) 212
D (-, -, -) (75.013, 0.011, 90.0) 53.4 (17.4, 0.0) 5
ITER
A
(33.750, 1.000, 90.0)
(32.750, 2.000, 80.0) (33.750, 1.002, 89.9) 50.6 (2.0, 0.1) 4.3
B (32.750, 2.000, -) (33.750, 1.002, 89.9) 50.6 (2.0, 0.1) 48
C (-, -, 80.0) (27.303, 1.716, 80.0) 1928.5 (6487.0, 10.0) 1143
D (-, -, -) (33.713, 0.989, 90.0) 82.8 (38.5, 0.0) 33
Real Scenarios
Map Scen.
ˆ
P
m
[m, m,
◦
]
ˆ
P
i
[m, m,
◦
]
ˆ
P
f
[m, m,
◦
] pp err. [mm] Rel. err. [mm,
◦
] RT[s]
Balcony
A
(1.700, 1.400, 330.0)
(1.700, 1.400, 330.0) (1.699, 1.452, 329.2) 44.6 (52.5, 0.8) 0.38
B (1.700, 1.400, -) (1.699, 1.452, 329.2) 44.6 (52.5, 0.8) 4.3
C (-, -, 330.0) (1.667, 1.457, 330.0) 79.6 (66.1, 0.0) 135
D (-, -, -) (1.599, 1.490, 330.7) 70.8 (64.3, 0.7) 1.4
IPFN
A
(14.750, 0.700, 180.0)
(14.750, 0.700, 180.0) (14.713, 0.665, 178.7) 26.3 (51.0, 1.3) 0.44
B (14.750, 0.700, -) (14.713, 0.665, 178.7) 26.3 (53.0, 1.3) 6.4
C (-, -, 180.0) (14.728, 0.707, 180.0) 41.6 (23.0, 0.0) 279
D (-, -, -) (14.720, 0.665, 178.7) 26.4 (46.7, 1.3) 7
a density of 50 points per meter except for the vot-
ing tests where the density was changed to 5 in or-
der to terminate the algorithm execution in a feasible
time. The results obtained for the balcony and corri-
dor maps are presented in table 1. The respective sec-
tion columns are identical to the columns of the sim-
ulated results explained before except for
ˆ
P
m
which
means pose measurements, consisting the only way
to first guess the initial pose (by hand measuring) so
a relative error column (“Rel. err”) was introduced.
Also images of the respective results are displayed in
Figures 8 and 9. The images follow the same layout
as the simulation figures stated above.
Figure 8: Balcony map experimental results.
Figure 9: IPFN map experimental results.
6 CONCLUSIONS
An algorithm to calibrate a LRF sensor network was
proposed. The outcome is an estimated pose for each
device in the network. Simulated and experimental
test results show a dependency of the pose estimate
error to the sensor and map description accuracy. The
developed algorithm receives three input parameters:
a map description of the environment, LRF data, and
an initial pose estimate for each device. The first two
are mandatory and the uncertainty associated with the
CalibrationofLaserRangeFindersforMobileRobotLocalizationinITER
547

last one defines a scenario which determines the algo-
rithm behavior. Regardless of the scenario, the map
is always converted to points in order to assess the
results using (1). The map point conversion density
should be chosen accordingly as the previous equa-
tion presents an O(n
2
) operation.
Whenever an initial pose estimate is completely
known, the ICP algorithm is executed. The final pose
estimate is revealed by applying the ICP resultant
rigid body transformation to the initial pose estimate.
This is the fastest and most accurate method but isn’t
robust against the presence of outliers in the LRF data
or map description. To reduce this negative effect, an
outlier rejection method is planned for future work.
An extreme scenario may occur when the pose
of the sensors is completely unknown. In this case,
ICP alone cannot be used because of its local min-
ima problem, therefore a developed vertex method is
applied. This method comprises two phases: first,
geometric features, as segment lines and vertexes,
are extracted and subsequently a matching technique
based on the geometric combination of these features
is preformed. The main obstacle here is to figure out
the best combination of threshold values that leads
to a correct feature extraction. The time complexity
is proportional to the number of extracted features.
Other techniques, not as reliant on threshold values,
are on future plans. As an alternative, a brute force
test was conducted where the map was divided in a
grid and for each point of the grid, the ICP was ex-
ecuted. The results for the asymmetrical map are
shown in Figure 10. Although much more time con-
suming than the vertex method, slightly better accu-
rate results were achieved.
Figure 10: ICP brute force result.
As for the intermediate scenario, only the position
or orientation estimate value is known. In the first
case, a brute force ICP is carried out in the given po-
sition for a set of predefined angles. For the second
case, a voting based algorithm is applied to assign a
estimate probability of the LRF position to each of
the map coordinates. The voting method can be time
consuming and a less accurate method due to a combi-
nations of high initial angle deviation, low map reso-
lution and symmetry. Nevertheless suggests a consis-
tent alternative and a case of study for a global search
method.
An accurate map is assumed although, in a real
case scenario, that might not be the case. In the pres-
ence of outliers in the scanned data or map misde-
scription, robustness tests show that a variation of 1%
is enough to produce an error ten times higher. These
results, in the case of this application, can compro-
mise the localization algorithm behavior, where the
poses of the devices are to be used. In order to im-
prove outliers robustness, the ICP algorithm can be
customized to include an outliers rejection method.
ACKNOWLEDGEMENTS
The work leading to this publication received finan-
cial support from “Fundação para a Ciência e Tec-
nologia” through project UID/FIS/50010/2013. This
publication reflects the views only of the author, and
Fusion for Energy cannot be held responsible for any
use which may be made of the information contained
therein.
REFERENCES
A. Tesini, J. P. (2008). The iter remote maintenance system.
Fusion Eng. Des., 83(7-9):810–816.
Antone, M. and Friedman, Y. (2007). Fully automated laser
range calibration. In Proc. BMVC, pages 66.1–66.10.
doi:10.5244/C.21.66.
Besl, P. and McKay, N. (1992). A method for registration
two 3-d shapes. IEEE Trans. Pattern Anal. and Mach.
Intell., 14(2):239–256.
Carlos Fernández, Vidal Moreno, B. C. (2010). Cluster-
ing and line detection in laser range measurements.
Robotics and Autonomous Sys., 58(5):720–726.
Censi, A. (2008). An ICP variant using a point-to-line met-
ric. Robotics and Automation, pages 19–25.
Darren Locke, C. G. (2014). Progress in the conceptual de-
sign of the iter cask and plug remote handling system.
Fusion Eng. Des., 89(9-10):2419–2424.
J. Ferreira, A. Vale, R. V. (2013). Vehicle localization sys-
tem using off-board range sensor network. Proc. of
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
548

the 8th IFAC Intelligent Autonomous Vehicles Sympo-
sium, 8(1):102–107.
J. Soares, R. Ventura, A. V. (2014). Human-robot interface
architecture for a multi-purpose rescue vehicle for re-
mote assistance. In Symposium on Fusion Technology.
K. S. Arun, T. S. Huang, S. D. B. (1987). Least-squares
fitting of two 3-d point sets. Pattern Analysis and Ma-
chine Intelligence, IEEE Transactions, 9(5):698–700.
K. Schenk, A. K. (2012). Automatic calibration of a station-
ary network of laser range finders by matching move-
ment trajectories. IEEE/RSJ Int. Conf. on Intelligent
Robots and Systems, pages 431–437.
Low, K.-L. (2004). Linear least-squares optimization for
point-to-plane ICP surface registration. Tech. report.
Markus-Christian Amann, Thierry Bosch, M. L. R. M.
M. R. (2000). Laser ranging: a critical review of
usual techniques for distance measurement. Opt. Eng.,
40(1):10–19.
Sebastian Thrun, J. L. (2008). Handbook of Robotics.
Springer.
Viet Nguyen, Stefan Gächter, A. M. N. T. R. S. (2007).
A comparison of line extraction algorithms using 2d
range data for indoor mobile robotics. Autonomous
Robots, 23(2):97–111.
Vincenzo Caglioti, Alessandro Giusti, D. M. (2008). Mu-
tual calibration of a camera and a laser rangefinder.
Proc. Int’l Conf. on Computer Vision Theory and Ap-
plications, pages 33–42.
CalibrationofLaserRangeFindersforMobileRobotLocalizationinITER
549
