LQG/LTR Versus Smith Predictor Control
for Discrete-time Systems with Delay
Dariusz Horla and Andrzej Kr´olikowski
Pozna´n University of Technology, Institute of Control and Information Engineering,
ul. Piotrowo 3a, 60-965, Pozna´n, Poland
Keywords:
LQG/LTR Control, Time-delay, Smith Predictor.
Abstract:
A simple LQG control with no control cost is considered for discrete-time systems with input delay. In such
case the loop transfer recovery (LTR) effect can be obtained especially for minimum-phase systems. The
robustness of this control is analyzed and compared with state prediction control whose robustness stability is
formulated via LMI. The robustness with respect to uncertain time-delay is considered including the control
systems with Smith predictor-based controllers. Computer simulations of a second-order stable, unstable and
nonminimum-phase systems with time-delay are given to illustrate the robustness and performance of the
considered controllers.
1 INTRODUCTION
The LQG/LTR control for discrete-time systems is a
well known problem investigated for example in (Tad-
jine et al., 1994) where the general design aspects of
loop transfer recovery (LTR) both at the input and
at the output of the system are presented. In (Ma-
ciejowski, 1985) the asymptotic case of LQG control,
i.e. when the control weighting factor tends to zero
is considered for both prediction and filtering type of
controller. The case of nonminimum-phase (nmph)
system is also discussed. Robust LQG/LTR control of
discrete-time systems with time-delay at the input (or
computation delay) is a specific problem within a gen-
eral LQG/LTR framework. In this context some re-
sults are given in the literature like: (Kinnaert, 1990),
(Kinnaert and Peng, 1990), (Zhang and Freudenberg,
1993). In (Kinnaert, 1990) the LQG/LTR problem
with respect to the system input is solved for the
square minimum-phase (mph) system with d-sample
delays. The generalization of results in (Kinnaert,
1990) are given in (Kinnaert and Peng, 1990) where
the recovery at both system input and system output
is investigated and the corresponding recovered loop
transfer matrices are derived. Further extension of
these results can be found in (Zhang and Freuden-
berg, 1993) where LQG/LTR problem was solved for
nmph systems with time-delays and explicit expres-
sions of sensitivity and loop matrices are derived for
the asymptotic behaviour of control system.
In this paper,the discrete-time Kalman filter based
LQG control with no control cost for input-delayed
systems with application of LTR technique is consid-
ered. The resulting robustness with respect to uncer-
tain delay for mph and nmph systems is analyzed and
compared to prediction based control (Gonzales et al.,
2012). Additionally, the Smith predictor-like controls
and their robustness properties to time-delay uncer-
tainty are analyzed by simulations of second-order
systems.
2 LQG/LTR FOR
DISCRETE-TIME SYSTEMS
WITH DELAY
The state-space discrete-time SISO system is given by
x
t+1
= Fx
t
+ gu
t−d
+ w
t
(1)
y
t
= h
T
x
t
+ v
t
(2)
where {w
t
} and {v
t
} are sequences of independent
random vector and scalar variables with zero mean
and covariances Ew
t
w
T
s
= Σ
w
δ
t,s
, Ev
t
v
s
= σ
2
v
δ
t,s
, and
d is a delay given as multiplicity of sampling period.
The system (1), (2) can be transformed to
x
p
t+1
= Fx
p
t
+ gu
t
+ w
p
t
(3)
y
t
= h
T
x
p
t−d
+ v
t
(4)
388
Horla D. and Krolikowski A..
LQG/LTR Versus Smith Predictor Control for Discrete-time Systems with Delay.
DOI: 10.5220/0005537003880397
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 388-397
ISBN: 978-989-758-122-9
Copyright
c
 2015 SCITEPRESS (Science and Technology Publications, Lda.)

where x
p
t
= x
t+d
and the Kalman filter estimate of x
p
t
is given by
ˆx
p
t/t
= F
p
[ˆx
T
t/t
,u
t−d
,· ·· ,u
t−1
]
T
(5)
where F
p
= [F
d
,F
d−1
g
,F
d−2
g,··· ,Fg,g] and the fil-
tered estimate ˆx
t/t
in terms of prediction ˆx
t/t− 1
fol-
lows from
ˆx
t/t
= ˆx
t/t− 1
+ k
f
˜y
p
t
(6)
where ˜y
p
t
= y
t
− h
ˆx
t/t− 1
is an innovation of output.
The Kalman predictor for x
t+1
in steady-state is given
by
ˆx
t+1/t
= Fˆx
t/t− 1
+ g
u
t−d
+ k
p
˜y
p
t
(7)
and its gain is
k
p
= FP
f
h
[h
T
P
f
h
+ σ
2
v
]
−1
(8)
where P
f
is the solution of Riccati equation
P
f
= FP
f
F
T
+ Σ
w
− FP
f
h
[h
T
P
f
h
+ σ
2
v
]
−1
h
T
P
f
F
T
(9)
The filter gain is
k
f
= P
f
h[h
T
P
f
h+ σ
2
v
]
−1
, (10)
so k
p
= Fk
f
in view of (8) and (10). Finally, combin-
ing (6) and (7) one gets
ˆx
t/t− 1
= Fˆx
t−1/t−1
+ g
u
t−d−1
(11)
The LQG control law
u
t
= k
T
c
ˆx
p
t/t
(12)
aims to minimize the cost function
J = E
∞
∑
t=0
y
2
t
, (13)
so the gain k
c
is
k
T
c
= −[g
T
P
c
g]
−1
g
T
P
c
F (14)
and P
c
is the solution of Riccati equation
P
c
= F
T
P
c
F − F
T
P
c
g
[g
T
P
c
g]
−1
g
T
P
c
F + Q (15)
When the weighting matrix Q is Q = h
h
T
and assum-
ing that the system (1), (2) is stabilizable, detectable,
mph and d = 0 in (1) then it can be shown (Tadjine
et al., 1994), (Maciejowski, 1985) that k
c
takes very
simple form
k
T
c
= −(h
T
g
)
−1
h
T
F. (16)
under the condition that h
T
g
6= 0 which implies that
system has a natural one-step delay in control chan-
nel.
If G(z) = h
T
(zI − F)
−1
g
is mph and k
c
takes a form
(16) then the transfer function G
f
(z) of compensator
defined by (6) and (12) can be manipulated into the
form
G
f
(z) = −zk
T
c
[zI − (I − k
f
h
T
)(F − g
k
T
c
)]
−1
k
f
=
= −zk
T
c
[zI − F + g
k
T
c
]
−1
k
f
, (17)
and the perfect recovery takes place, that is
∆(z) = Φ(z) − G(z)G
f
(z) = 0, (18)
where the filter’s open-loop return ratio Φ(z) is
Φ(z) = h
T
(zI − F)
−1
k
p
. (19)
When G(z) is nmph then the perfect recovery is in
general not possible (this will be commentedlater on).
Similarly, it is interesting to see what happens when
the LTR procedure is applied for system (1), (2) with
time-delay.
Time-delay in control channel of the system (1), (2)
can alternatively be characterized by taking d = 0 in
(1) and assuming that delay is incorporated in the sys-
tem (F, g
,h) with the Markov parameters fulfilling the
following properties
h
T
g = h
T
Fg = · ·· = h
T
F
r−2
g = 0, h
T
F
r−1
g 6= 0
(20)
for r ≥ 1. It is known that the smallest integer r satis-
fying the above properties is the relative degree of the
system. It is worthy noting that for relative degree r
and time-delay d in (1) it holds r = d + 1.
In (Zhang and Freudenberg, 1993), (Kinnaert and
Peng, 1990) it was shown that for mph systems the
error function ∆(z) for
k
T
c
= −(h
T
F
r−1
g)
−1
h
T
F
r
. (21)
has a form
∆(z) = h
T
(I − z
−(r−1)
F
r−1
)(zI − F)
−1
k
p
(22)
for r ≥ 1. In general ∆(z) 6= 0, so the perfect recovery
cannot be obtained except the case r = 1 that corre-
sponds to (18).
2.1 Comments on nmph Systems
As already mentioned LTR for nmph systems is rec-
ommended because the partial recovery could be
achieved (Zhang and Freudenberg, 1993). The re-
sult for mph systems can be modified for the nmph
systems after the proper factorization of Φ(z) (Zhang
and Freudenberg, 1993). For every nmph system the
all-pass factorization is possible
G(z) = h
T
(zI − F)
−1
g
= G
a
(z)G
m
(z) =
= G
a
(z)h
T
m
(zI − F)
−1
g
(23)
LQG/LTRVersusSmithPredictorControlforDiscrete-timeSystemswithDelay
389

where G
a
(z) is all-pass and G
m
(z) is mph stable trans-
fer function. Partial recovery (∆(z) 6= 0) for time-
delayed system is then possible with LQG control
gain
k
T
c
= −(h
T
m
F
r−1
g
)
−1
h
T
m
F
r
. (24)
where h
m
can be easily obtained as a function of sys-
tem parameters.
The recovery error is now
∆(z) = (h
T
− z
−(r−1)
G
a
(z)h
T
m
F
r−1
)(zI − F)
−1
k
p
.
(25)
It is worth noting, as shown in (Zhang and Freuden-
berg, 1993), that full recovery is possible in the sense
of loop transfer function Φ(z) if the following condi-
tions are fulfilled
• Φ(z) = G
a
(z)h
T
m
(zI − F)
−1
Fk
f
,
• h
T
Fk
f
= h
T
F
2
k
f
= ·· · = h
T
F
r
k
f
= 0.
This means that the observer loop has the same nmph
structure and at least as many delay steps as the sys-
tem.
2.2 LMI Approach
In (Gonzales et al., 2012) an LMI condition for robust
stability of noise-free system (1) with unknown time-
delay belonging to known interval, i.e. d
l
≤ d ≤ d
u
is
given. The system is under the state feedback pre-
diction based controller u
t
= k
T
c
ˆx
t+h/t
with a given
gain k
c
and a given prediction horizon h. This ap-
proach is adopted for our comparison study where
h = d and ˆx
t+d/t
can be obtained e.g. from (5), (6),
(7) neglecting the noise terms. Then the following
corollary follows: the global closed-loop stability re-
sult given in (Gonzales et al., 2012) reads: for any k
T
c
such that F + g
k
T
c
is Hurwitz and for d
l
= d
u
= h = d
there exists a feasible solution, i.e. there exist matri-
ces P,L, Q,Q
m
,Q
M
,Q
d
,Z,Z
1
,Z
2
,M > 0 that satisfy

Γ 0
0 −Z
M

< 0 (26)
where
Γ =









Γ
1
0 0 0 Γ
3
Γ
4
Γ
5
∗ Γ
6
0 0 0 Γ
9
Γ
10
∗ ∗ Γ
11
0 Z
1
0 0
∗ ∗ ∗ Γ
12
0 0 0
∗ ∗ ∗ ∗ Γ
13
−Γ
9
−Γ
10
∗ ∗ ∗ ∗ ∗ −L 0
∗ ∗ ∗ ∗ ∗ ∗ −M









.
and Γ
1
= −P + Q + Q
m
+ Q
M
+ Q
d
− Z
2
,Γ
3
=
Z
2
,Γ
4
= A
T
1
,Γ
5
= (A
1
−I)
T
,Γ
6
= −Q, Γ
9
= B
T
1
,Γ
10
=
B
T
1
,Γ
11
= −Q
m
,Γ
12
= −Q
M
,Γ
13
= −Q
d
− Z
1
−
Z
2
,Z
M
= Z − d
2
Z
1
,A
1
= F + g
k
T
c
,B
1
= F
d
g
k
T
c
,PL =
I,ZM = I, with
Q = ε
1
I,Q
m
= ε
1
I,Q
M
= ε
1
I,Q
d
= ε
1
I,Z = ε
1
I,M =
ε
−1
1
I,Z
1
= ε
2
I,Z
2
= ε
2
I for some positive small
enough scalars ε
1
,ε
2
.
It is interesting to note that the stabilizable and de-
tectable system with arbitrarily large delay in the con-
trol input can be asymptotically stabilized by either
linear state or output feedback as long as the open
loop system is not asymptotically unstable (Zongli,
2007). The additive uncertain system with input time-
delay and possible unstable poles was considered in
(A. Kodjina and Ishijima, 1994), where it was shown
that achievable robustness margin decreases to zero as
the time-delay value increases. Problem of time-delay
compensation for nonlinear systems was tackled in
(Kravaris and Wright, 1989) using Smith Predictor-
based controllers.
3 SMITH-PREDICTOR
APPROACH
Among the variety of Smith Predictor controllers, a
PID Smith Predictor (PIDSP) controller (Bobal et al.,
2011) was derived so that the desired closed-loop
transfer function is
1−e
−α
1−z
=1
where α =
T
s
T
m
and T
m
is
desired time constant of the first-order closed-loop re-
sponse. For a second-order system the controller has
a form
u
t
= q
0
ε
t
+ q
1
ε
t−1
+ q
2
ε
t−2
+ u
t−1
(27)
where q
0
= γ, q
1
= a
1
γ, q
2
= a
2
γ, γ = (1−e
−α
)/(b
1
+
b
2
). The error is ε
t
= r
t
− ˆy
p,t
where r
t
is the reference
signal and the signal ˆy
p,t
is calculated as ˆy
p,t
= ˆe
p,t
+
ˆy
m,t
with ˆe
p,t
= y
t
− ˆy
t
, ˆy
t
= G
d
ˆy
m,t
, y
t
= G
p
u
t
, ˆy
m,t
=
G
m
u
t
, and finally the PID controller (27) is described
by
u
t
= G
c
(z
−1
)ε
t
.
This gives the output-reference closed-loop transfer
function
G
cl
(z
−1
) = (28)
G
p
(z
−1
)G
c
(z
−1
)
1+ G
p
(z
−1
)G
c
(z
−1
) + G
m
(z
−1
)G
c
(z
−1
)(1− G
d
(z
−1
))
that in case of perfect matching, i.e.
G
m
(z
−1
)G
d
(z
−1
) = G
p
(z
−1
) (d = d
m
) yields
G
cl
(z
−1
) =
G
p
(z
−1
)G
c
(z
−1
)
1+ G
m
(z
−1
)G
c
(z
−1
)
(29)
For the second-order model
G
p
(z
−1
) =
b
1
z
−1
+ b
2
z
−2
1+ a
1
z
−1
+ a
2
z
−2
z
−d
, (30)
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
390

considered below in the simulations, the specific
transfer functions are
G
m
(z
−1
) =
z
−1
(b
1
+ b
2
)
A(z
−1
)
and
G
d
(z
−1
) =
z
−d
m
B(z
−1
)
z
−1
(b
1
+ b
2
)
.
It is easy to check from (29) that for a second-order
model (30) in steady state one obtains G
cl
(1) = 1, i.e.
perfect tracking for perfect matching.
Consider now the Smith predictor idea presented in
(Kravaris and Wright, 1989) for continuous-time sys-
tem and apply it to discrete-time state-space frame-
work. Then for the noise-free system (1), (2) the con-
trol law is
u
t
=
det(zI − F)
det(zI − F) + k
T
c
Ad j(zI − F)g
(1− z
−d
m
)
(v
t
+k
T
c
x
t
),
(31)
where v
t
is a command signal, d
m
is the time-delay in
the model and the state x
t
= (zI − F)
−1
gz
−d
u
t
. The
closed-loop discrete-time transfer function from y
t
to
v
t
takes a form
G
cl
(z
−1
) = (32)
h
T
Ad j(zI − F)g
det(zI − F) − k
c
Ad j(zI − F)g
(1+ z
−d
− z
−d
m
)
z
−d
With this form it is possible to select closed-loop
poles for the delayed system according to the pole-
placement method. The feedback gain k
c
calculated
using (14) can also be applied. To obtain the asymp-
totic tracking accuracy defined by the error ε
t
= r
t
−y
t
the feedforward gain k
r
is introduced, i.e. v
t
= k
r
r
t
where k
r
= G
cl
(1)
−1
.
Finally, the error feedback controller described for ex-
ample in (Soroush and Kravaris, 1992) is considered.
When the condition (20) is fulfilled then it holds
G(z
−1
) = z
−r
[h
T
F
r
(zI − F)
−1
g
+ h
T
F
r−1
g
] =
= z
−r
G
r
(z
−1
). (33)
Suppose the required closed-loop response is of the
simple first-order with time-delay
G
cl
(z
−1
) =
1− α
1− αz
−1
z
−r
. (34)
then the controller has the following transfer function
from ε to u
t
G
c
(z
−1
) =
1− α
1− αz
−1
− (1− α)z
−r
1
G
r
(z
−1
)
(35)
where 0 < α < 1 and the error is ε
t
= r
t
− y
t
. When
the time-delay mismatch occurs the relative degree
r
m
in the model should be used in (35), noting that
r
m
= d
m
+ 1. The corresponding closed-loop transfer
function is then
G
cl
(z
−1
) = (36)
(1− α)G
r
(z
−1
)
z
r−1
(z−a)G
r
m
(z
−1
)+(1−α)z
r−r
m
(G
r
m
(z
−1
)−G
r
(z
−1
))
Obviously, for perfect matching we get (34).
4 LTR FOR ARMAX MODEL
The ARMAX model is given by
y
t
= G(z
−1
)u
t−d
+ G
e
(z
−1
)e
t
(37)
where G(z
−1
) =
B(z
−1
)
A(z
−1
)
, G
e
(z
−1
) =
C(z
−1
)
A(z
−1
)
, and at the
same time G(z) = h
T
(zI − F)
−1
g
, G
e
(z) = h
T
(zI −
F)
−1
k
e
+ 1 with A(z
−1
),B(z
−1
) and C(z
−1
) polyno-
mials in the operator z
−1
, i.e. A(z
−1
) = 1 + a
1
z
−1
+
...+a
n
z
−n
,B(z
−1
) = b
1
z
−1
+...+b
n
z
−n
,C(z
−1
) = 1+
c
1
z
−1
+...+ c
n
z
−n
and {e
t
} assumed to be a sequence
of independent variables with zero mean and variance
σ
2
e
.
ARMAX model (37) has an equivalent innovation
state-space representation
x
t+1
= Fx
t
+ g
u
t−d
+ k
e
e
t
(38)
y
t
= h
T
x
t
+ e
t
(39)
where g
= (b
1
,..., b
n
)
T
, k
e
= (c
1
− a
1
,..., c
n
−
a
n
)
T
, h
T
= (1,0,..., 0)
F =



−a
1
1 ... 0
. . ... 0
−a
n−1
. ... 1
−a
n
. ... 0



.
Equations (38), (39) can take the following represen-
tation
x
t+1
= F
∗
x
t
+ gu
t−d
+ k
e
y
t
(40)
y
t
= h
T
x
t
+ e
t
, (41)
where F
∗
= F − k
e
h
T
. Kalman predictor associated
with eq.(40) is
ˆx
t+1/t
= F
∗
ˆx
t/t
+ g
u
t−d
+ k
e
y
t
(42)
and Kalman filter is given by
ˆx
t/t
= ˆx
t/t− 1
+ k
f
(y
t
− h
T
ˆx
t/t− 1
), (43)
with filter gain
k
f
= P
f
h
[h
T
P
f
h
+ σ
2
e
]
−1
(44)
LQG/LTRVersusSmithPredictorControlforDiscrete-timeSystemswithDelay
391

where P
f
is the solution of Riccati equation
P
f
= F
∗
P
f
F
∗T
− F
∗
P
f
hh
T
P
f
F
∗T
(h
T
P
f
h
+ σ
2
e
)
−1
.
(45)
The predictor equation derived from (42) is
ˆx
t+1/t
= F ˆx
t/t− 1
+ g
u
t−d
+ k
p
(y
t
−
ˆ
h
T
ˆx
t/t− 1
), (46)
where the predictor gain is now k
p
= k
∗
p
+k
e
and k
∗
p
=
F
∗
k
f
.
However, in the considered steady state case, the so-
lution of (45) is P
f
= 0 and consequently k
f
= k
∗
p
= 0
and ˆx
t/t
= ˆx
t/t− 1
= ˆx
t
. From (46) or directly from (42)
the Kalman filter equation takes then a simple form
ˆx
t+1
= F
∗
ˆx
t
+ g
u
t−d
+ k
e
y
t
(47)
Taking this filter form into account together with
(21) or (24) one can see that in order to imple-
ment LQG/LTR control no Riccati equation has to be
solved neither for k
c
nor for k
f
.
5 SIMULATION STUDY
First, consider the stable system
G(s) =
s+ 2
(s+ 1)(s+ 3)
e
−s
discretized with ZOH and sampling period T
s
= 0.5s
which yields the following transfer function in z
−1
G(z
−1
) =
−0.3262z
−1
− 0.1224z
−2
1− 0.8297z
−1
+ 0.1535z
−2
z
−2
, (48)
so d = 2.
Next, an example of second-orderunstable time-delay
system is
G
p
(s) =
s+ 2
(s+ 1)(s− 3)
e
−s
and its discrete-time form with ZOH and T
s
= 0.5s is
G
p
(z
−1
) =
1.352z
−1
− 0.439z
−2
1− 5.088z
−1
+ 2.718z
−2
z
−2
. (49)
Finally, nmph time-delay system is considered
G
p
(s) =
−s+ 1
(s+ 1)(s+ 2)
e
−s
which after discretization yields the followingtransfer
function in z
−1
G
p
(z
−1
) =
−0.1612z
−1
+ 0.2856z
−2
1− 0.9744z
−1
+ 0.223z
−2
z
−2
. (50)
The nominal model in z operator is
G(z) =
−0.1612z+ 0.2856
z
2
− 0.9744z+ 0.223
. (51)
with one nmph zero at 1.772. Then one can calculate
G
a
(z) =
z− 1.772
1− 1.772z
and according to (23) and (24)
h
T
m
= (0.5452, 1.3077), k
T
c
= (−0.8391,−1.9091).
In computer tests different configurations of delay d
in the system and its model d
m
in the controller were
tested. In other words the undermodeling d
m
< d and
overmodeling d
m
> d cases are analyzed.
Simulations of closed-loop step responses with Smith
predictor based controllers have been tested for stable
and nmph systems as they are not suitable for unstable
systems.
An example run of step responses for controller (27)
is shown in Fig.1, for stable system with d = 2 and
d
m
= 2,6,10 and for d
m
= 2 and d = 2, 6, 10. Re-
sponses for the same configuration of time-delays for
controller (31) is shown in Fig.2, and corresponding
situation for controller (35) in Fig.3.
An analogous run of step responses for nmph system
and controllers (27), (31), (35) with the same time-
delays configurations is shown in Figs.4, 5, 6, corre-
spondingly.
One can observe some performance difference be-
tween all these controllers. Looking at the responses
one may say that controller (35) slightly outperforms
others and in case of nmph system there is no typical
undershoot because of pole-zero cancelation in opem-
loop.
LQG/LTR method with control (21) as well as LMI
approach (26) applied to stable and nmph systems
give stability for all under- and overmodeling con-
figurations of time-delay. For unstable systems the
global closed-loop stability with respect to time-delay
can not be assured even in case of perfect matching
d = d
m
.
The obtained values of destabilizing time-delay for
LQG/LTR method are d
dest
= 5, d
dest
= 4 for con-
trollers (14) and (21), respectively and for the noise
variance σ
2
e
= 0.01. For variance value σ
2
e
= 0.001
one obtains d
dest
= 10, d
dest
= 11 for controllers (14)
and (21), respectively. One may observe that the
smaller the variance the larger value of d
dest
, so the
value of d
dest
depends on stochastic properties of
noise. In considered case the performance of both
controllers (14), (21) is comparable, however con-
troller (21) is computationally simpler. Additionally,
unstable nmph system was simulated with controllers
(14), (21), (24) yielding the same result d
dest
= 5 for
σ
2
e
= 0.01. For variance σ
2
e
= 0.001, the values of
d
dest
= 5,6, 7 are obtained correspondingly for con-
trollers (14), (21), (24).
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
392

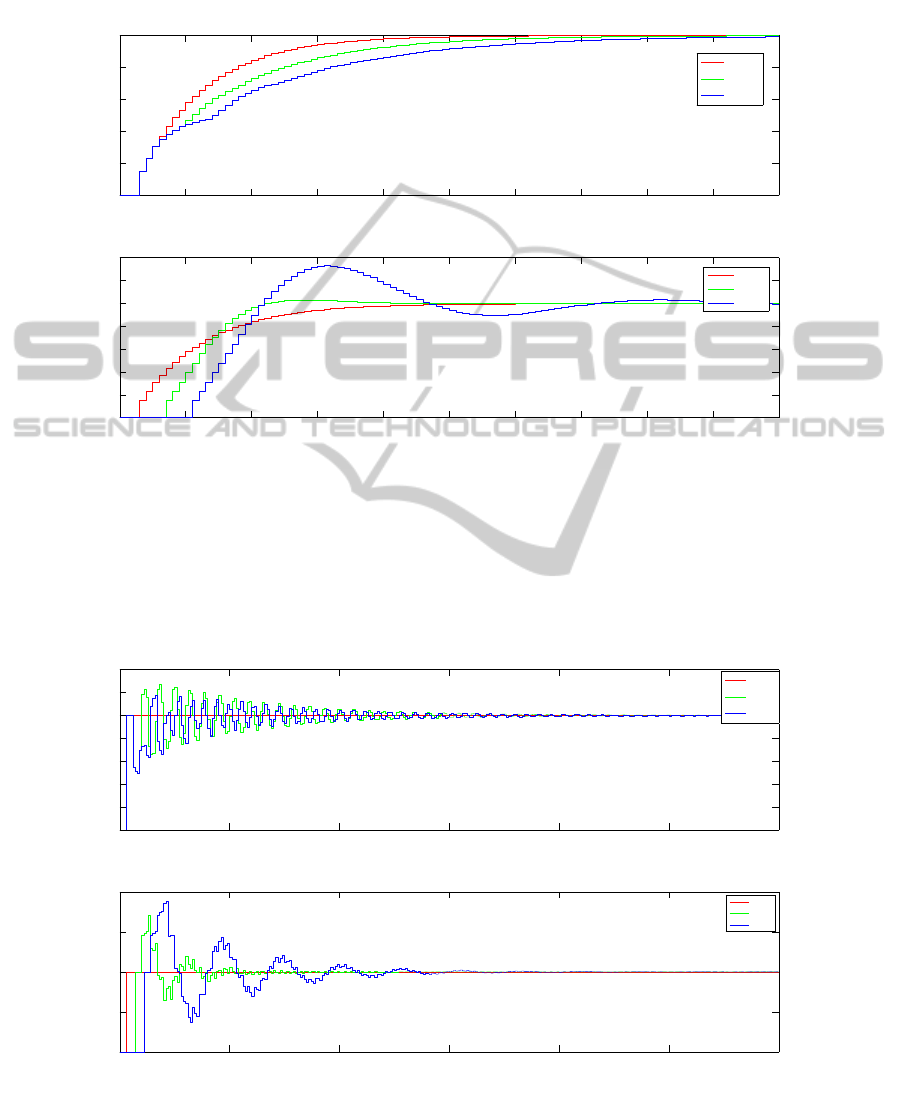
0 10 20 30 40 50 60 70 80 90 100
0
0.2
0.4
0.6
0.8
1
t
y
t
d=2
d
m
=2
d
m
=6
d
m
=10
0 10 20 30 40 50 60 70 80 90 100
0
0.2
0.4
0.6
0.8
1
1.2
1.4
t
y
t
d
m
=2
d=2
d=6
d=10
Figure 1: Step responses for stable system with controller (27).
0 50 100 150 200 250 300
0
0.2
0.4
0.6
0.8
1
1.2
1.4
t
y
t
d=2
d
m
=2
d
m
=6
d
m
=10
0 50 100 150 200 250 300
0
0.5
1
1.5
2
t
y
t
d
m
=2
d=2
d=6
d=10
Figure 2: Step responses for stable system with controller (31).
LQG/LTRVersusSmithPredictorControlforDiscrete-timeSystemswithDelay
393

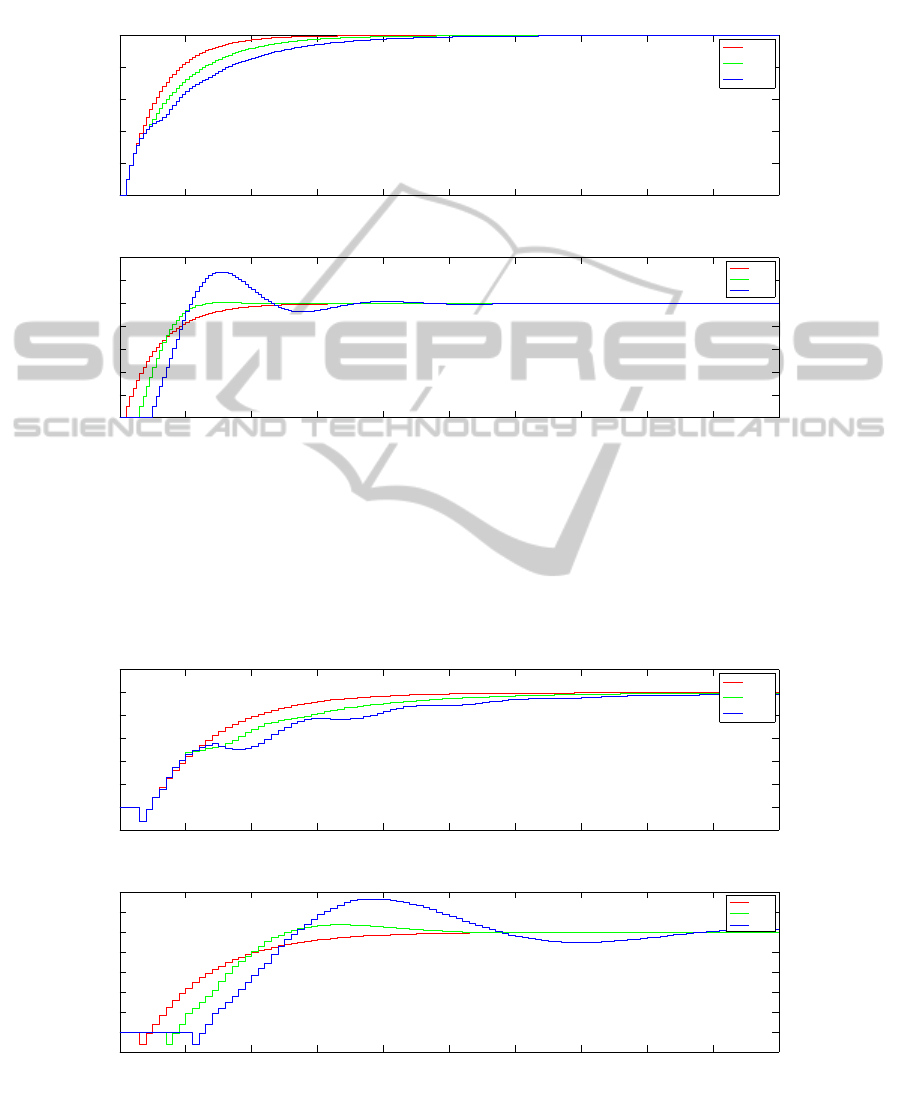
0 20 40 60 80 100 120 140 160 180 200
0
0.2
0.4
0.6
0.8
1
t
y
t
d=2
d
m
=2
d
m
=6
d
m
=10
0 20 40 60 80 100 120 140 160 180 200
0
0.2
0.4
0.6
0.8
1
1.2
1.4
t
y
t
d
m
=2
d=2
d=6
d=10
Figure 3: Step responses for stable system with controller (35).
0 10 20 30 40 50 60 70 80 90 100
−0.2
0
0.2
0.4
0.6
0.8
1
1.2
t
y
t
d=2
d
m
=2
d
m
=6
d
m
=10
0 10 20 30 40 50 60 70 80 90 100
−0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
t
y
t
d
m
=2
d=2
d=6
d=10
Figure 4: Step responses for nmph system with controller (27).
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
394

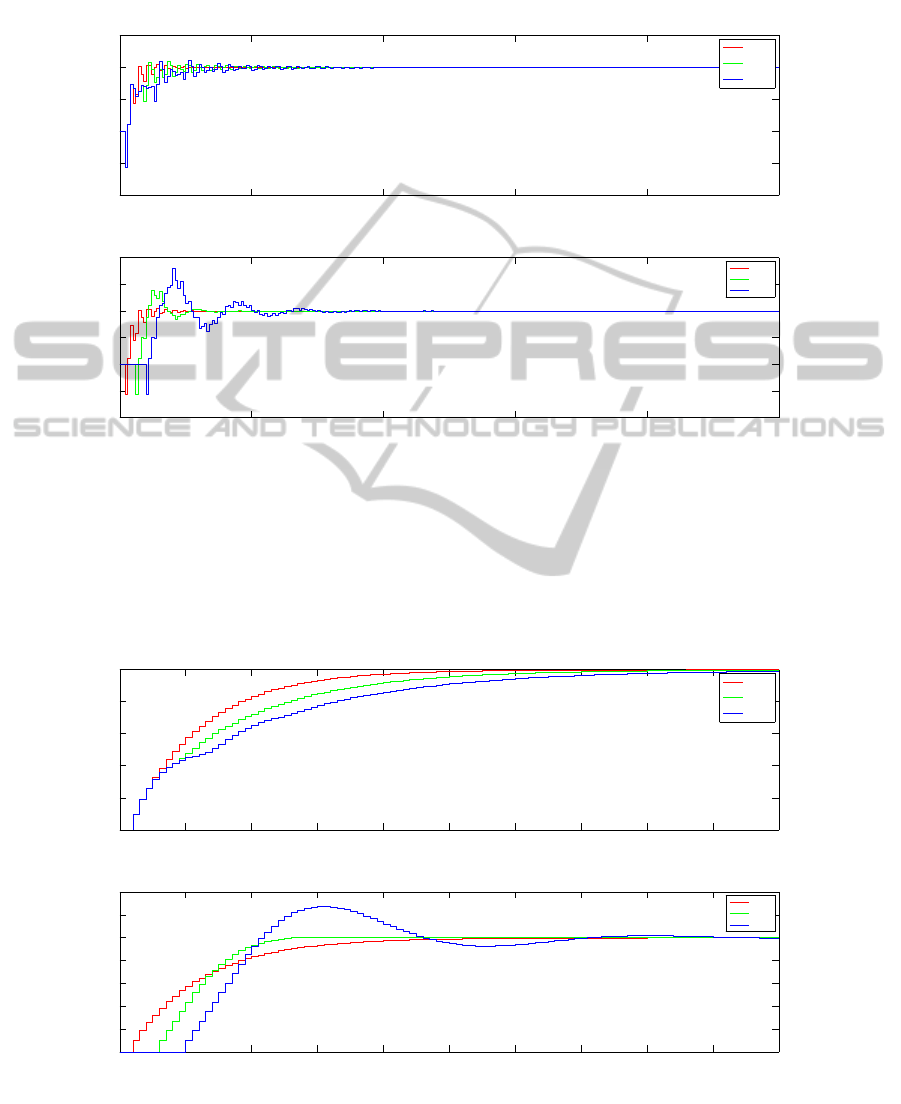
0 50 100 150 200 250
−1
−0.5
0
0.5
1
1.5
t
y
t
d=2
d
m
=2
d
m
=6
d
m
=10
0 50 100 150 200 250
−1
−0.5
0
0.5
1
1.5
2
t
y
t
d
m
=2
d=2
d=6
d=10
Figure 5: Step responses for nmph system with controller (31).
0 10 20 30 40 50 60 70 80 90 100
0
0.2
0.4
0.6
0.8
1
t
y
t
d=2
d
m
=2
d
m
=6
d
m
=10
0 10 20 30 40 50 60 70 80 90 100
0
0.2
0.4
0.6
0.8
1
1.2
1.4
t
y
t
d
m
=2
d=2
d=6
d=10
Figure 6: Step responses for nmph system with controller (35).
LQG/LTRVersusSmithPredictorControlforDiscrete-timeSystemswithDelay
395

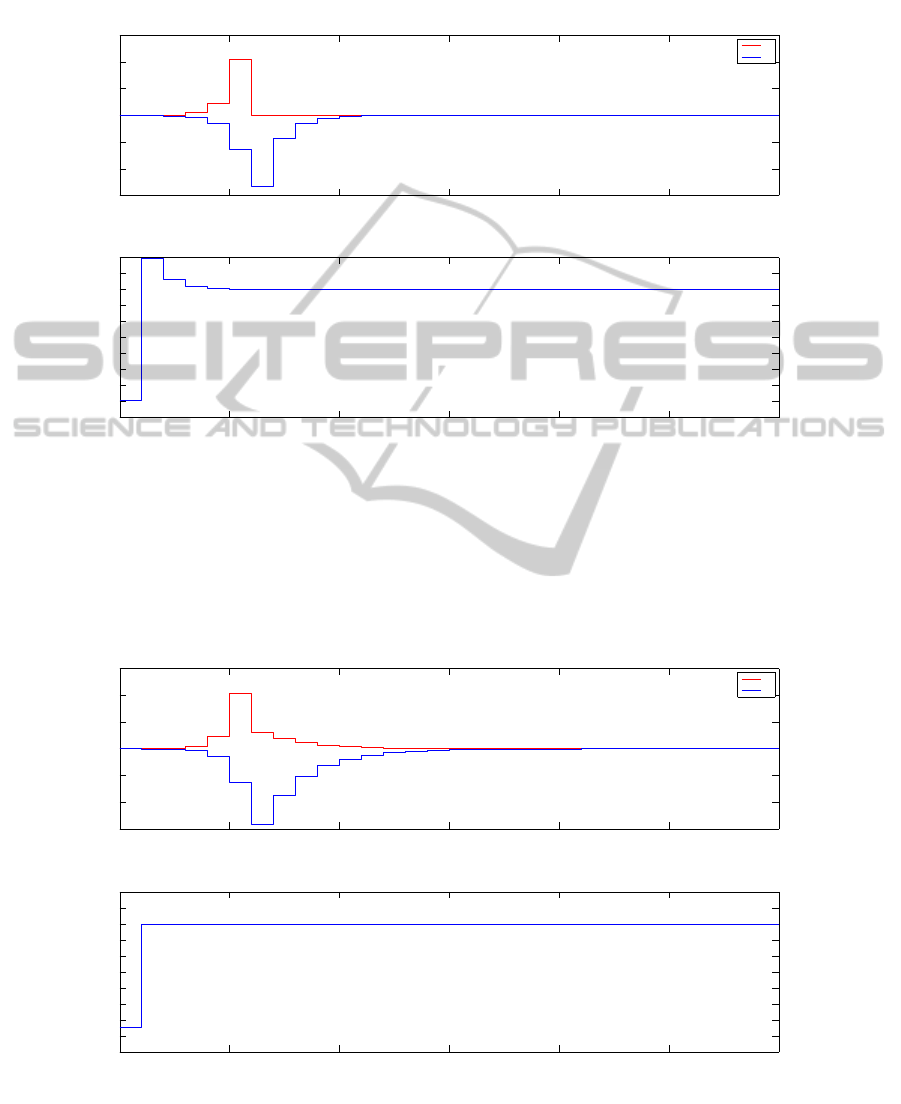
0 5 10 15 20 25 30
−8000
−7000
−6000
−5000
−4000
−3000
−2000
−1000
0
1000
2000
t
u
t
0 5 10 15 20 25 30
−3000
−2000
−1000
0
1000
2000
3000
d=d
m
=5
t
x
1,t
x
2,t
Figure 7: Control and state variables for unstable system with controller (14).
0 5 10 15 20 25 30
−8000
−7000
−6000
−5000
−4000
−3000
−2000
−1000
0
1000
2000
t
u
t
0 5 10 15 20 25 30
−3000
−2000
−1000
0
1000
2000
3000
d=d
m
=5
t
x
1,t
x
2,t
Figure 8: Control and state variables for unstable system with controller (21).
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
396

Simulation of state feedback prediction control,
whose stability condition is given by LMI (26), for an
unstable system is performed for the feedback gain
k
c
from (14). For scalars ε
1
= ε
2
= 10
−6
the ob-
tained value of destabilizing time-delay of the system
is d
dest
= 14, however, it should be remembered that
this is for deterministic system. This value may be
considered as a limit value of d
dest
for LQG/LTR as
a noise variance decrease, i.e. as the system becomes
more deterministic.
Plots of state variables and control for unstable noise-
free system with non-zero initial conditions and d =
d
m
= 5 are given in Figs.7, 8 for controllers (14) and
(21), respectively.
6 CONCLUSIONS
LQG control of discrete-time SISO system with time-
delay in the context of LTR effect is presented and
comparedwith LMI robust stability condition given in
(Gonzales et al., 2012). Moreover, the Smith predic-
tor approach for PID controller, state space controller
and error feedback controller are included into anal-
ysis of robust stability with respect to the modeling
error of time-delay. This is done on the basis of sim-
ulations of second-order system with given nominal
time-delay value. Results show some potential of the
LQG method with LTR effect as a way for robustify-
ing the stability of closed-loop control for stochastic
systems with time-delay and possible unstable open-
loop system.
REFERENCES
A. Kodjina, K. Uchida, F. S. and Ishijima, S. (1994). Robust
stabilization of a system with delays in control. IEEE
Trans. Automat. Contr., 39(8):1694–1698.
Bobal, V., Chalupa, P., Dostal, P., and Novak, J. (2011).
Simulation verification of digital self-tuning control
of systems with time-delay. In Proc. IAESTED Int.
Conf., pages CD ROM 66–71, Crete, Greece.
Gonzales, A., Sala, A., and Albertos, P. (2012). Predic-
tor based stabilization of discrete time-varying input-
delay systems. Automatica., 48(4):454–457.
Kinnaert, M. (1990). Lqg/ltr technique for discrete-time
systems with time-delays. In Proc. of the 20th Con-
ference on Decision and Control, pages 1633–1634,
Honolulu, Hawaii.
Kinnaert, M. and Peng, Y. (1990). Discrete-time lqg/ltr
technique for systems with time delays. Systems and
Control Letters, 15:303–311.
Kravaris, C. and Wright, R. (1989). Dead-time com-
pensation for nonlinear processes. AIChE Journal,
35(9):1535–1542.
Maciejowski, J. (1985). Asymptotic recovery for discrete-
time systems. IEEE Trans. Automat. Contr.,
30(6):602–605.
Soroush, M. and Kravaris, C. (1992). Discrete-time nonlin-
ear controller synthesis by input/output linearization.
AIChE Journal, 38(12):1923–1945.
Tadjine, M., M’Saad, M., and Dugard, L. (1994). Discrete-
time compensators with loop transfer recovery. IEEE
Trans. Automat. Contr., 39(6):1259–1262.
Zhang, Z. and Freudenberg, J. (1993). Discrete-time loop
transfer recovery for systems with nonminimum phase
zeros and time delays. Automatica, 29(2):351–365.
Zongli, L. (2007). On asymptotic stabilizability of discrete-
time-linear systems with delayed input. Communica-
tions in Information and Systems., 7(3):227–264.
LQG/LTRVersusSmithPredictorControlforDiscrete-timeSystemswithDelay
397