Multiple Sensor Fusion using Adaptive Divided Difference
Information Filter
Aritro Dey, Smita Sadhu and Tapan Kumar Ghoshal
Department of Electrical Engineering, Jadavpur University, Kolkata, 700032, India
Keywords: Sensor Fusion, Information Filter, Process Noise Covariance, Adaptive Filter, State Estimation.
Abstract: This paper addresses the problem of multiple sensor fusion in situations where the system dynamics suffers
from unknown parameter variation. An adaptive nonlinear information filter has been proposed for such
multi sensor estimation problems where the process noise covariance becomes unknown as a consequence
of unknown parameter variation. The proposed filter, based on the Divided Difference interpolation
formula, ensures satisfactory estimation performance by online adaptation of the unknown process noise
covariance and makes sensor fusion successful. Efficacy of the proposed filter is demonstrated with the help
of a tracking problem in a sensor fusion configuration. Results from Monte Carlo simulation indicate that
though the process noise covariance is unknown, the performance of the proposed filter is demonstrably
superior to its non adaptive version in the context of joint estimation of parameter and states.
1 INTRODUCTION
Sensor fusion is a conventional process of
integration of information from multiple sensors
(homogeneous as well as heterogeneous sensors) to
provide sufficiently reliable and enriched knowledge
of the unmeasured states of the system under
observation. Sensor fusion is extensively employed
method which may find many real life applications,
like, target tracking in collaborative sensor networks
(Vercauteren, 2005), sensor fusion in the fields of
robot navigation, intelligent vehicle, surveillance
(Lee, 2008). Formulation of an estimation problem
and its solution is one of the central aspects of
successful sensor fusion. The Information filter
variant of state estimators is widely recommended
for multiple sensor estimation (Jia, 2013), (Liu,
2011), (Ge, 2014) and plays a significant role in
sensor fusion. Because of simple computation
methodology and easy initialization (Anderson,
1979) Information filters are preferred over the
traditional estimators with the standard error
covariance form.
For multiple sensor estimation several nonlinear
information filters viz., Unscented information
filters (Lee, 2008) , Central Difference information
filters (Liu, 2011), Cubature and higher order
cubature information filters (Jia, 2013), (Ge, 2014)
have been reported in literature where the task of
multi sensor estimation is found to be satisfactory
only when the process noise and the measurement
noise covariances are precisely known. Improper
choice of noise covariance deteriorates estimation
results as it is also observed for nonlinear estimation
problem using the traditional nonlinear filters.
Unavailability of the knowledge of process noise
covariance because of unknown parameter variation
or the process noise statistics is, therefore, a serious
issue of multiple sensor fusion which needs
attention. An arbitrary choice of process noise
covariance degrades the estimation results and the
nonlinear information filter may even face
divergence.
This paper presents a new algorithm for
Adaptive Divided Difference Information filter
(ADDIF) which is intended for situations when
enough knowledge of system dynamics is
unavailable due to parametric uncertainty. In such
cases the process noise covariance becomes
unknown. The proposed filter based on divided
difference interpolation formula (Nørgaard, 2000)
ensures satisfactory estimation performance by
adapting online the unknown process noise
covariance with ensured positive definiteness.
Because of the unavailability of the proof for
convergence like other information filters the
superiority of the proposed filter is established with
the help of an extensive Monte Carlo simulation.
398
Dey A., Sadhu S. and Ghoshal T..
Multiple Sensor Fusion using Adaptive Divided Difference Information Filter.
DOI: 10.5220/0005537303980406
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 398-406
ISBN: 978-989-758-122-9
Copyright
c
 2015 SCITEPRESS (Science and Technology Publications, Lda.)

In this paper the adaptation rule is
mathematically established and incorporated in the
algorithm of Divided Difference Information filter,
alias, Central Difference Information filter (Liu,
2011) to circumvent the problem of the unknown
process noise covariance. The method for adaptation
of process noise covariance (Q) in the proposed
filter is based on ‘Maximum Likelihood Estimation’
which is inspired from the early works on adaptive
filters (Maybeck, 1982), (Mohamed, 1999) for linear
signal models. The adaptive sigma point filters with
standard error covariance form have been reported in
the literatures which are developed extending the
concept of adaptation for linear signal models.
Adaptive UKF (Das, 2013), (Hajiyev, 2014), (Lee,
2005), (Soken, 2014) adaptive DDF (Lee, 2005)
have been cited in literatures. A Q adaptive first
order DDF is presented by (Lee, 2005) where the
state residual has been used for adaptation. A robust
adaptive second order DDF is presented by
(Karlgaard, 2011) where, in lieu of adaptation, focus
is on robustness. However, formulation of adaptive
nonlinear information filter has not yet been reported
in literature to the best knowledge of the authors.
The proposed Q adaptive information filter
intended for sensor fusion has the following
advantages: (i) Unlike Extended Information Filter
and its higher order relatives computation of
complex Jacobian and Hessian matrices are not
required. (ii) As the proposed filter is based on
Divided Difference Information filter it does not
need tuning parameters like Unscented Information
filter and can reportedly achieve same accuracy at a
lower computational burden (Liu, 2011). (iii)
Positive definiteness of the adapted process noise
covariance is ensured. (iv) The proposed filter has
the flexibility of multiple sensor estimation even in
face of unknown noise covariance because of its
dual aspect of information filter framework and Q
adaptation algorithm.
2 ADAPTIVE DIVIDED
DIFFERENCE INFORMATION
FILTER
In this section the problem statement is provided
followed by the solution methods which include the
algorithm for the proposed filter.
2.1 Problem Statement
We consider an augmented nonlinear dynamic
system as given below.
k1kk
wxfx +=
−
)(
(1)
()
ζ
kk
ζζ
k
vxgy +=
(2)
Here
n
k
Rx ∈
is an augmented state vector, By
the term augmented state vector, it is meant that the
unknown parameters have been concatenated with
the state vector such that dimension of the
augmented state vector is n. The difference
equations corresponding to a typical unknown
parameter
k
ζ
are considered to obey the random walk
model, i.e.,
ζ
k1kk
wζζ +=
−
, where
ζ
k
w
is the noise
term.
),(~
k
n
k
Q0Rw ∈
indicates zero mean process
noise (Gaussian) with unknown noise covariance.
mζ
k
Ry ∈
is the measurement available from
the
th
ζ
sensor among
M
different sensors where
M,,1 =
ζ
. The measurement noise of each sensor
is considered to be white (Gaussian) and denoted as,
)(~
ζ
mζ
k
R0,Rv ∈
. It is also considered the
covariances of the sensors are known. The process
noise covariance,
k
Q
, however, remains unknown for
parametric uncertainty and needs to be adapted.
2.2 Filtering Algorithm
Initialization:
Initialize
ζ
R,Q,P,x
000
ˆ
ˆ
ˆ
Time update steps:
calculate
)
ˆ
(
ˆ
1kx
P1)(kS
−
=− FactorCholesky
(3)
Propagation of a-priori estimate of state:
()(){}

=
−−−
−
−+++=
n
p
hh
nh
hh
1
2
1
ˆˆˆˆ
)
ˆ
(
22
2
px,1kpx,1k1kk
sxfsxfxfx
(
4)
where
px,
s
ˆ
is p
th
column of
1)(kS
x
−
ˆ
and the interval
length is chosen as,
3=h
for Gaussian distribution
following (Nørgaard, 2000).
Propagation of a-priori error covariance:
The a-priori error covariance is
[][]
Q(k)S(k)S(k)S(k)SP
(2)
xx
(1)
xx
(2)
xx
(1)
xxk
+=
T
ˆˆˆˆ
(5)
where
()
{}
()(()){}
jx,1kijx,1kiji,
(1)
xx
sxfsxfS
ˆˆˆˆ
2
1
ˆ
hh(k)
h
−−+=
−−
(6)
()
{}
ji,
(1)
xx
(k)S
ˆ
indicates the element (e
ij
) of
(k)S
(1)
xx
ˆ
.
(k)S
(1)
xx
ˆ
is first order approximation of the
square root of a-priori error covariance based on
MultipleSensorFusionusingAdaptiveDividedDifferenceInformationFilter
399

interpolation formulae (Nørgaard, 2000).
(k)S
(1)
xx
ˆ
is to
be computed using (6) for i=1,…,n and j=1,…,n.
()
{}
()(()
())














−
−++
=
−
−−
−
1ki
jx,1kijx,1ki
ji,
(2)
xx
xf
sxfsxf
(k)S
ˆ
2
ˆˆˆˆ
2
2
2
1
ˆ
hh
h
h
(7)
(k)S
(2)
xx
ˆ
is the second order approximation to be
computed in a similar way using (7).
The predicted information matrix
k
Z
and
information vector
k
z
are related with the predicted
estimate and error covariance as :
1
kk
PZ
−
=
(8)
kkk
xZz =
(9)
Compute
(k)S
x
such that it is a Cholesky factor
of
k
P
. This factor has been involved for
measurement update steps.
)(
kx
P(k)S FactorCholesky=
(10)
Measurement update steps:
For
M,,1 =
ζ
the following steps are to be
executed:
Propagation of a-priori estimate of measurement:
()()
{}

=
−
−+++=
n
p
hh
nh
hh
1
2
1
22
2
)(
px,k
ζ
px,k
ζ
k
ζζ
k
sxgsxgxgy
(11)
The cross covariance is
[][]
T
(k)S(k)SP
(1)
xyx
xy
k
=
(12)
where
()
{
}
()
(
()
)
{
}
jx,kjx,kji,
(1)
xy
sxgsxg(k)S hh
ii
h
−−+=
ζζ
2
1
(13)
()
{
}
ji,
(1)
xy
(k)S
in the similar way of (6) for i=1,…,m
and j=1,…,n
Computation of Pseudo Measurement Matrix:
Now, to make the information contribution
equations compatible to those of the EIF, a pseudo-
measurement matrix is defined by (14) following the
approach of (Lee, 2008).
()
T
xy
k
1
k
ζ
k
PPΨ
−
=
(14)
Computation of information state contribution and
its associated matrix:
Each sensor presents local information state
contribution and its associated information matrix as
()()()
k
ζ
k
ζ
k
1
ζ
k
ζ
k
ζ
k
xΨRΨφ +=
−
ϑ
T
(15)
()()
ζ
k
1
ζ
k
ζ
k
ζ
k
ΨRΨΦ
−
=
T
(16)
Multi Sensor Estimation:
For reliable estimation the information regarding the
measurements obtained from all the sensors are
combined using the Divided Difference information
filter. The decentralized approach has been followed
for multiple sensor estimation to economize
computational effort.
As described in the problem statement,
measurements are available from
th
ζ
sensor
where
M,,1 =
ζ
. The local information state
contribution and its associated information matrix
from each sensor can be obtained by (15) and (16).
The measurement update for the information vector
and information matrix after fusion is simply
expressed as a linear combination of these local
information contribution terms by:

=
+=
M
1ζ
ζ
kkk
φzz
ˆ
(17)

=
+=
M
1ζ
ζ
kkk
ΦZZ
ˆ
(18)
The a posteriori estimates of systems state and error
covariance matrix are extracted using the formula
by:
k
1
kk
zZx
ˆ
ˆ
ˆ
−
=
(19)
1
kk
ZP
−
=
ˆˆ
(20)
Computation of state residual:
The state residual is defined as
kkk
xxρ −=
ˆ
(21)
Adaptation of process noise covariance:
Using the estimated residual covariance from a
sliding window (size N) the adapted Q can be
expressed as

+−=
=
k
Nkj
N
1
1
ˆ
T
kkk
ρρQ
(22)
The adapted
k
Q
ˆ
of current instant can be used in (5)
to refine
k
P
so that the measurement update can be
further refined by re-computation of (11) to (20).
Adaptation step is mathematically derived and
provided in the subsection 2.3.
2.3 Q –Adaptation Steps
The Q adaptation formula used in the proposed
algorithm is derived using MLE technique. The
steps followed for derivation of adapted Q are
inspired from the work of (Maybeck, 1982),
(Mohamed, 1999) for linear signal models. The
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
400

probability density function of the measurements
conditioned on adaptive parameter,
α
at specific
epoch k is chosen based on innovation sequence. It
should be borne in mind that the algorithm presented
in the paper is meant for multiple sensor fusion
problems. Hence, for the simplicity of the
mathematical derivation we augment all the
available measurements to get a single measurement
vector as
[]
T
M
kkkk
ϑϑϑϑ 
21
=
with order mM.
Therefore, the corresponding measurement noise
covariance becomes
()
M
diag
kkkk
RRRR ,,,
21
=
and the
pseudo measurement matrix can be expressed as
()
M
diag
kkkk
ΨΨΨΨ ,,,
21
=
The likelihood function is chosen following
(Mohamed, 1999) as
()
()
()
k
1T
k
k
k
C
C
P ϑϑ
π
ϑ
ϑ
α
−
−=
2
1
exp
2
1
mM
y
k
(23)
or,
()
()
()
{}
k
1T
k
k
k
CCP ϑϑπ
ϑϑ
α
−
++−= ln2ln
2
1
ln mM
k
y
(24)
Multiplying both sides with −2 and neglecting the
constant term we get
k
1T
k
k
k
CC ϑϑ
ϑϑ
−
+= lnE
(25)
Innovation sequence has been considered inside
a window size N as the filter uses a fixed length
memory. The innovation inside the window will be
summed. Therefore, the Maximum Likelihood
condition becomes:
()






+

=
−
k
jj
jj
j
j
0
lnmin ϑϑ
ϑϑ
1T
CC
(26)
which results in
0
0
=
















∂
∂
−


















∂
∂

=
−−−
k
jj
j
j
tr
j
1
k
1T
j
k
1
j
j
j
C
α
C
C
α
C
C ϑϑ
ϑ
ϑ
ϑ
ϑ
ϑ
(27)
0
0
=


























∂
∂
−


















∂
∂

=
−−−
k
jj
trtr
j
j
k
1T
jj
1
k
1
α
C
CC
α
C
C
j
jj
ϑ
ϑϑ
ϑ
ϑ
ϑϑ
(28)
[]
0
0
=


























∂
∂
−

=
−−−
k
jj
j
tr
k
1T
jj
11
α
C
CCC
j
jj
ϑ
ϑϑϑ
ϑϑ
(29)
The formulae for matrix operation are given
in(Mohamed, 1999). Here, tr indicate trace of matrix
and j
0
=k−N+1. The deduction of the relation
between innovation covariance,
k
ϑ
C
and the
measurement noise covariance,
k
R
necessitates the
augmented pseudo measurement matrix of the
nonlinear measurement equation. The use of the
pseudo measurement matrix is justified as reported
in (Lee, 2008), (Soken, 2015).
Using the pseudo measurement matrix the
innovation covariance can be represented as:
T
kkkk
ΨPΨRC
−
+=
k
ϑ
(30)
For adaptation of Q, the adaptive parameter
α
is
chosen as
iii
Qα =
()
T
kk
k
k
k
ΨP
Q
Ψ
Q
C
kk
k
∂
∂
=
∂
∂
ϑ
(31)
[][]
T
k
(2)
xx
(1)
xx
(2)
xx
(1)
xx
k
k
k
Ψ
Q
(k)S(k)S(k)S(k)S
Q
Ψ
Q
C
j








+
∂
∂
=
∂
∂
k
T
kk
ˆˆˆˆ
ϑ
(32)
The term
[][]
T
(k)S(k)S(k)S(k)S
(2)
xx
(1)
xx
(2)
xx
(1)
xx
ˆˆˆˆ
is
analogous to the a priori error covariance when
process noise covariance is absent. It is assumed
following the work of (Mohamed, 1999) that the
within the estimation window the a priori error
covariance is in steady state. Hence the derivative of
this term may be ignored.
Substituting this value in the ML equation we get
[]
()
{} []
0
0
=−

=
−−−
k
jj
jj
j
tr
T1T
jj
11
IΨΨCCC
jj
ϑϑϑ
ϑϑ
(33)
Alternatively,
[] {} []
0
0
=−

=
−−−
k
jj
jj
j
tr ΨCCCΨ
1T
jj
11T
jj
ϑϑϑ
ϑϑ
(34)
[] {} []
0
0
=−

=
−−−
k
jj
jjjj
tr ΨCCΨΨCΨ
1T
jj
1T1T
jjj
ϑϑϑ
ϑϑ
(35)
{}
[]
0
0
=−

=
−−−
k
jj
j
T
jjjjjj
tr
1T
jj
11
PKKPΨKP ϑϑ
(36)
(){}
[]
0
0
=−

=
−−
k
jj
j
T
jjjjjj
tr
1T
jj
1
PKKPΨKP ϑϑ
(37)
The term
k
ϑ
k
K
can also be represented as
kkkk
xxK −=
ˆ
ϑ
, which the state residual.
kkk
xxρ −=
ˆ
(38)
Equation (35) can, therefore, be expressed as
(){}
[]
0
0
=−

=
−−
k
jj
jjjjj
tr
1T
jj
1
PρρPΨKP
(39)
The expression of
k
P
ensures the positive
definiteness of
k
P
. Therefore, above expression
vanishes only when
MultipleSensorFusionusingAdaptiveDividedDifferenceInformationFilter
401

(){}
[]
0
0
=−

=
k
jj
jjj
tr
T
jj
ρρPΨK
(40)
(){} []
0
ˆ
0
=−−

=
k
jj
jj
tr
T
jj
ρρPP
(41)
[]

=
=−
k
jj
N
0
1
ˆ
T
jjkk
ρρPP
(42)
Using (5)
k
P
can be replace as
[][]
[]

=
=−+
k
jj
k
T
N
0
1
ˆ
ˆ
ˆˆˆˆ
T
jjk
(2)
xx
(1)
xx
(2)
xx
(1)
xx
ρρPQ
(k)S(k)S(k)S(k)S
(43)
[]
[][]
()
T
k
jj
k
N
(k)S(k)S(k)S(k)SP
ρρQ
(2)
xx
(1)
xx
(2)
xx
(1)
xxk
T
jj
ˆˆˆˆ
ˆ
1
ˆ
0
−+
=

=
(44)
As recommended in (Mohamed, 1999) the term
[][]
(
)
T
(2)
xx
(1)
xx
(2)
xx
(1)
xxk
(k)S(k)S(k)S(k)SP
ˆˆˆˆ
ˆ
−
becomes often
low and may be negligible during steady state.
Hence, adapted Q is approximately represented by
[]

=
=
k
jj
k
N
0
1
ˆ
T
jj
ρρQ
(45)
2.3.1 Notes on Adaptation
The expression (45) given above has been presented
in a simplified approach. Mathematically derived
expression of adapted Q is given by (44). The term
[
]
[
]
(k)S(k)S(k)S(k)S
(2)
xx
(1)
xx
(2)
xx
(1)
xx
ˆˆˆˆ
of a posteriori
error covariance
k
P
ˆ
is implicitly dependent on
k
P
ˆ
and acquires a steady value (often low) as the filter
approaches steady state. Therefore, ignoring their
effect from the adapted Q is justified and does not
induce large error in the adapted Q. This
approximation as mentioned in (Mohamed, 1999)
for linear systems is followed here so that the
symmetry and the positive definiteness of adapted Q
can be ensured. Otherwise singularity cannot be over
ruled. Because of this assumption the adaptation
becomes more accurate as the filter reaches steady
state.
It is to be noted that the expression (45) which
same as (22) is appropriate only when the step index
k is greater than or equal to the window length N .
When the step index
k
is less than N , adaptation
begins with available state residual. The window
length is gradually increased till it reaches the
desired window length
N . Afterward the sliding
window concept becomes appropriate.
The window size N, should be appropriately
chosen considering several factors. A smaller
window size generally ensures lower computational
burden but reportedly may be prone to divergence. A
larger window size ensures unbiased estimates.
However, it is not suitable for short term variation in
process noise covariance.
3 CASE STUDY
The performance of adaptive DDIF is demonstrated
using a problem of multi sensor tracking of an
aircraft which is executing a maneuvering turn. The
dynamic model of the system is presented in two
dimensional spaces as given in (Jia, 2013). The turn
rate of the aircraft is considered to be unknown and
time varying which makes the tracking problem
significantly nonlinear. Therefore, this problem may
be an appropriate one to validate the performance of
the proposed Q adaptive information filter.
3.1 System Dynamics
The dynamic equation of the above mentioned
tracking problem is presented below. The turn rate
of the aircraft being unknown it is modelled as a
state and augmented with the state vector of the
system model. As knowledge about the nature of
variation of the unknown turn is unavailable the
augmented parameter is considered to follow a
simple random walk model. The dynamic model is
taken from the work of (Jia,2013).
() ()
() ()
() ()
() ()
kk
kk
kk
k
w
k
k
k
k
k
k
k
k
+
















−
=
−
−−
−
−−
−
−
−
−
−
−
−
−
−
1
11
sincos1
11
1cossin
10000
0cos0sin0
010
0sin0cos0
001
1
1
1
1
1
1
1
1
ξ
τωτω
τωτω
ξ
ω
τω
ω
τω
ω
τω
ω
τω
(46)
where the state vector
[]
T
kyyxxk
kkkk
vpvp ωξ =
;
k
x
p
and
k
y
p
are the
position in x and y coordinate;
k
x
v
and
k
y
v
are the
corresponding velocity components at the instant k.
τ
indicates the time interval between two
consecutive measurements.
k
w
is zero mean
Gaussian noise (white) which indicates the modeling
error. The process noise for this noise sequence is
considered as
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
402

















=
τ
τ
τ
τ
ττ
τ
ττ
q
Q
k
0000
01.000
000
0001.0
000
2
1.0
2
1.0
3
1.0
2
1.0
2
1.0
3
1.0
2
23
2
23
(47)
Note, that the element
() 5,5
k
Q
is the noise
covariance of corresponding augmented parameter,
i.e., turn rate. As the turn rate is unknown and time
varying the accurate knowledge of q is unavailable
and has to be assumed for traditional non adaptive
information filter. However, for simulation study we
have considered
()
2
12
s rad10323.1
−−
×=q
to generate
the true state trajectories.
The trajectories of the aircraft are tracked by the
fusion of the bearing angle signal from two tracking
radars located in two different places. The
measurement equation can be represented as
2,1tan
1
=+








−
−
=
−
ζθ
ζ
ζ
ζ
ζ
k
xx
yy
k
v
pp
pp
refk
refk
(48)
ζ
indicates position of the
th
ζ
radar.
;10;10
4141
mpmp
refref
xy
−=−= mpmp
refref
xy
4242
10;10 ==
. The zero mean measurement noise (Gaussian) has
covariances
()
2
1
30mradR =
and
()
2
2
40mradR =
.
The interval between two successive measurements,
sec1=
τ
.
3.2 Simulation Procedure
The proposed filter for sensor fusion has been
evaluated with help of an extensive Monte Carlo
simulation with 10000 runs. True state trajectories
are generated with an initial state
[]
T
x
111
0
s rad05235.0ms0m1000ms300m1000
−−−
−=
and the unknown element q
true
.The filter is
initialized with a Gaussian prior with mean
0
x and
0
ˆ
P
, where
[
]
(
)
4
0
101010010100
ˆ
−
= diagP
. As
the element q
true
is practically unknown, we assume
q
filter
to be 20 times higher q
true
during initialization
of the filter. The choice of a high q
filter
is justified as
it indicates high degree of uncertainty about the
nature of variation of unknown time varying turn
rate.
Note that only the element of Q which is
associated with the turn rate is unknown while the
other elements are known. Therefore, we need to
adapt the element of Q related to turn rate leaving
the other known element frozen at the truth value. It
can be verified from the derivation of adapted Q that
partial differential is taken with respect to each
diagonal element of Q. Therefore, the adaptation
formula can easily be reformulated only for the
unknown elements. More details are provided in
(Dey, 2014).
Root means square error (RMSE) for position,
velocity and turn rate are computed for performance
analysis of the proposed filter. The RMSE for
position and velocity are computed using the
formula given in (Jia, 2013).
()()

=






−+−=
mc
N
i
ikikikik
mc
N
RMSE
1
2
,,
2
,,
ˆˆ
1
lljj
eξeξeξeξ
(49)
where j=1 and l=3 for RMSE of position
estimation. For RMSE of velocity estimation j=2
and l=4. RMSE for turn rate estimation is obtained
with j=5 and replacing the unit vector
l
e by a zero
vector.
Further investigation with this tracking problem
revealed that this particular bearing only tracking
problem is susceptible to track losses because of its
measurement equation. It has been considered that
the turn rate is unknown and time varying. As a
consequence the trajectory of the aircraft become
such that the difference between the bearing angle
from two different radars may either be negligibly
small or become closer to
π
. Practically the line of
sight of two radars does not intersect each other to
find the object in some of such situations.
Consequently the measurement loses its uniqueness
of information as the aircraft tracked by the radar
cannot be specifically located in the atmosphere with
the measured bearing angles. It is to be noted that in
the work of (Jia, 2013) which has considered the
same tracking problem track loss phenomenon has
not been discussed. The authors have presented a
representative run for illustration where track loss
occurs for the non adaptive filter in ideal case when
knowledge of process noise covariance is available.
The performance of the proposed filter has also been
compared to its non adaptive counter part in context
of its susceptibility to track losses. To detect the
occurrence of track loss a condition has been
considered as given below.
()( )
myyxx
kkkk
800
ˆˆ
22
≥−+−
∞
(50)
If the condition given by (50) is satisfied it is
understood that the estimated trajectory fails to track
the true trajectory of the aircraft. Such a situation for
a representative run is illustrated by Figure 1 where
in the ideal case the non adaptive DDIF with known
Q fails to track the trajectory.
MultipleSensorFusionusingAdaptiveDividedDifferenceInformationFilter
403

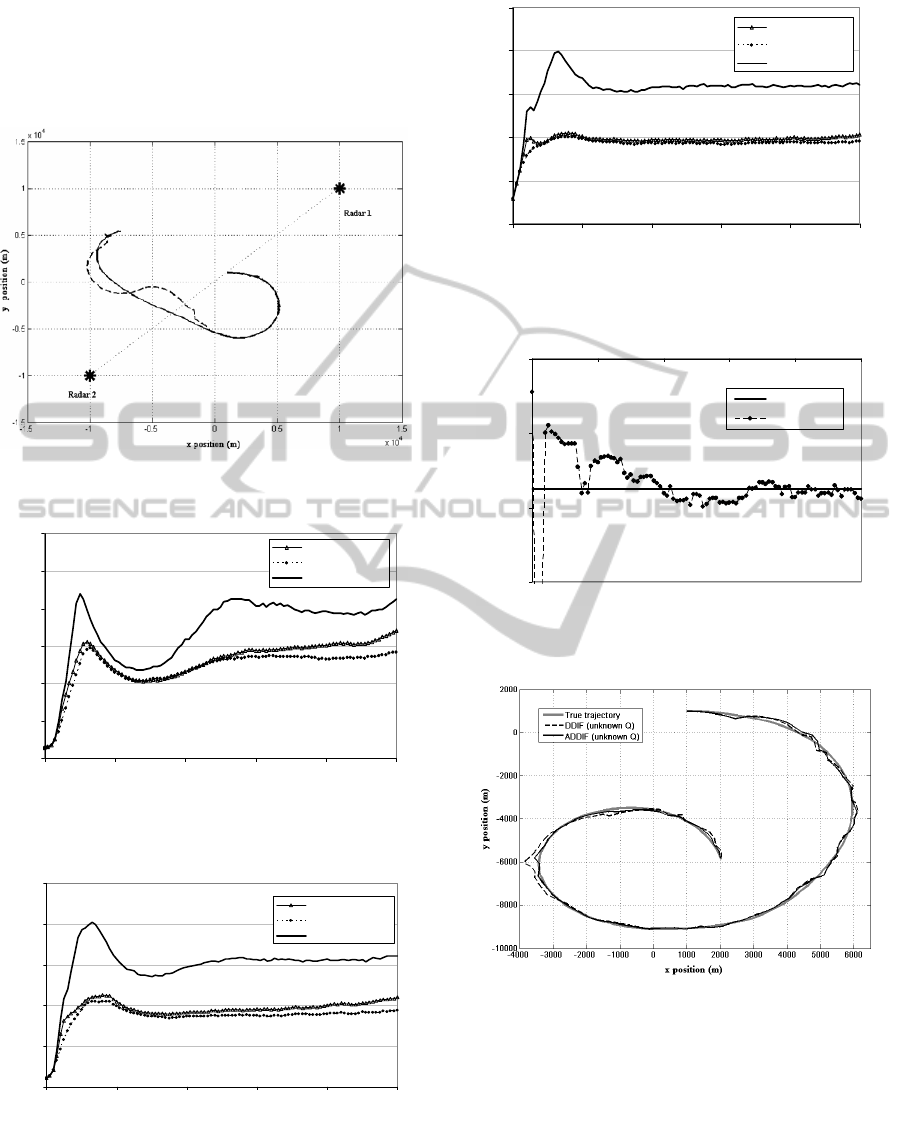
In case of Monte Carlo simulation the track loss
cases are detected and those error sequences are
omitted while calculating the RMS errors. The track
loss count from 10000 Monte Carlo run are also
presented for each filter in percentage.
Figure 1: A representative run to illustrate track loss for
the ideal case when non adaptive DDIF has known
Q.
0
50
100
150
200
250
300
0 20 40 60 80 100
time (sec)
RMSE - position (m)
ADDIF
DDIF (Q known)
DDIF (Q unknown)
Figure 2: Comparison of RMS error (position estimation)
of ADDIF & DDIF for 10000 MC runs.
0
20
40
60
80
100
0 20406080100
time (sec)
RMSE - velocity (m/sec)
ADDIF
DDIF (Q known)
DDIF (Q unknown)
Figure 3: Comparison of RMS error (velocity estimation)
of ADDIF & DDIF for 10000 MC runs.
0
1
2
3
4
5
0 20406080100
time (sec)
RMSE - turn rate (deg/sec)
ADDIF
DDIF (Q known)
DDIF (Q unknown)
Figure 4: Comparison of RMS error (turn rate estimation)
of ADDIF & DDIF for 10000 MC runs.
0.00001
0.0001
0.001
0.01
0 20406080100
time (sec)
TrueQ and Adapted
Q
Q(5,5)-truth
Q(5,5)- adapted
Figure 5: Plot of estimated process noise covariance (Q
5,5
)
for a representative run.
Figure 6: Tracking performance of ADDIF and non
adaptive DDIF with unknown
Q for a run.
3.3 Simulation Results
From the results of Monte Carlo simulation,
performance of proposed ADDIF is compared with
that of non adaptive DDIF in the situation when the
turn rate of the aircraft is unknown and time varying.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
404

 It has been observed from Figure 2, Figure 3
and Figure 4 that the performance of ADDIF is
substantially superior to that of non adaptive
DDIF as the RMSE for all three states
converged to a lower steady state value within
comparatively less time. RMSE of non
adaptive DDIF deteriorates as the Q remains
unknown due to unknown turn rate.
 It is to be also pointed out that though the
elements of Q related to position and velocity
are known RMSE of position and velocity for
the non adaptive DDIF is degraded because of
the implicit influence of poorly estimated turn
rate.
 Figure 5 indicates that for ADDIF the unknown
process noise element is converged to the truth
value in about 30 sec.
 The RMSE results of ADDIF are also
compared with non adaptive DDIF in the ideal
situation when q is known only to the latter.
Though this comparison may sound unusual,
this comparison illumines on how far the
performance ADDIF even with unknown Q is
close to the performance of traditional filter in
ideal situation with known Q. It is
demonstrated that the RMSE of ADDIF for all
the states are very closed to that nature of
RMSE of non adaptive filter in ideal condition.
The initial mismatch in RMSE is because of
the time taken for adapted Q to converge.
 It is also found from the Monte Carlo
simulation that the track loss cases cannot be
ruled out even for the ideal situation when the
non adaptive DDIF has the knowledge of Q. In
the MC simulation 1.7% of track loss has been
observed for the ideal case. When Q is
unknown, the percentage of track loss for
ADDIF is 2.2% and that for non adaptive
DDIF is 15%. The track loss percentage for
ADDIF is comparable with the ideal case and
substantially low compared its non adaptive
version which is prone to track loss cases.
These observations indicate the superiority of
ADDIF over non adaptive DDIF when Q remains
unknown for parametric uncertainties.
4 CONCLUSIONS
An Adaptive Divided Difference Information filter
has been proposed for multiple sensor fusion in face
of unknown parameter variation and exemplified
with the help of an aircraft tracking problem. The
proposed filter is found to carry out multiple sensor
estimation successfully by online adaptation of
process noise covariance (Q) where the knowledge
of Q remains unavailable due to parametric
uncertainty. The adapted Q from the filter converges
on the true value of Q and continues to track it for
subsequent time. The results from Monte Carlo
study indicate that the RMS error performance of the
proposed filter, as expected, is significantly superior
to the non adaptive Divided Difference Information
filter in face of unknown Q. Because of the
capability of adaptation, flexibility for multiple
sensor estimation and good error settling
performance the proposed filter may be a
recommended for multiple sensor fusion for the
systems affected by unknown parameter variation.
ACKNOWLEDGEMENTS
The First author thanks Council of Scientific &
Industrial Research (CSIR), New Delhi, India for
financial support and expresses his gratitude to
Centre for Knowledge Based System, Jadavpur
University, Kolkata, India for infrastructural
support.
REFERENCES
T. Vercauteren, and X. Wang., 2005. Decentralized sigma-
point information filters for target tracking in
collaborative sensor networks. In IEEE Trans. Signal
Processing
, 53 (8), 2997-3009.
D. J. Lee, 2008. Nonlinear estimation and multiple sensor
fusion using unscented information filtering. In
IEEE
Signal Processing Letters
, 15, 861-864.
B. Jia, M. Xin, K. Pham, E. Blasch, & G. Chen, 2013.
Multiple sensor estimation using a high-degree
cubature information filter. In conference
SPIE
Defense, Security, and Sensing. International Society
for Optics and Photonics
, 87390T-87390T.
G. Liu, F. Worgotter and I. Markelic, 2011. Nonlinear
estimation using central difference information filter.
In
IEEE Workshop Statistical Signal Processing. 593-
596.
Q. Ge, Daxing Xu, and Chenglin Wen, 2014. Cubature
information filters with correlated noises and their
applications in decentralized fusion. In
Journal of
Signal Processing
, 94, 434-444.
B. D. O. Anderson and J.B. Moore, 1979.
Optimal
Filtering
, Prentice Hall, Englewood Cliffs, 1
st
edition.
M. Nørgaard, N. K. Poulsen, and O. Ravn, 2000. New
developments in state estimation for nonlinear
systems. In
Automatica, 36 (11), 1627-1638.
MultipleSensorFusionusingAdaptiveDividedDifferenceInformationFilter
405

P. S. Maybeck, 1982. Stochastic models, estimation, and
control
, Academic Press, New York, 1st edition.
A. H. Mohamed and K. P. Schwarz, 1999.Adaptive
Kalman filtering for INS/GPS. In Journal of geodesy,
vol. 73 (4), 193-203.
M. Das, S. Sadhu, T. K. Ghoshal, 2013. An Adaptive
Sigma Point Filter for Nonlinear Filtering Problems.
In International Journal of Electrical, Electronics and
Computer Engineering
, 2 (2), 13-19.
C. Hajiyev, H. E. Soken, 2014. Robust adaptive unscented
Kalman filter for attitude estimation of pico satellites.
In
International Journal of Adaptive Control and
Signal Processing
, 28 (2), 107-120.
D. J. Lee, 2005. Nonlinear Bayesian filtering with
applications to estimation and navigation,. PhD thesis,
Texas A&M University.
H. Soken, S. Sakai, 2015. Adaptive Tuning of the UKF for
Satellite Attitude Estimation. In
Journal of Aerospace
Engineering
, 28 (3), DOI: 10.1061/(ASCE)AS.1943-
5525.0000412.
C. D. Karlgaard, H. Schaub, 2011. Adaptive nonlinear
Huber-based navigation for rendezvous in elliptical
orbit, In Journal of Guidance, Control, and Dynamics,
34 (2), pp. 388-402.
A, Dey, S. Sadhu, T.K. Ghoshal, 2014. Adaptive Gauss
Hermite Filter for Parameter Varying Nonlinear
Systems. In International Conference on Signal
Processing and Communication
, 1-5, DOI:
10.1109/SPCOM.2014.6983948.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
406