The Optimal Control Problems of Nonlinear Systems

M. N. Kalimoldayev, M. T. Jenaliyev, A. A. Abdildayeva and L. S. Kopbosyn

Institute of Informational and Computational Tehnologies, MES RK, Pushkin Str. 125, Almaty, Kazakhstan

eywords:

Electric Power System, Nonlinear System, Phase System, Control Synthesis, Bellman-Krotov Function.

Abstract:

This article discusses the optimal control problem of nonlinear systems, which are described by ordinary dif-

ferential equations, their right parts are periodic in the angular coordinate. The particularity of the considered

in the given work nonlinear control problems is that they take into account the fact that on unfairly long interval

of time, preservation of a deviation of any subsystem of controlled system from nominal operating conditions

conducts to danger of destruction and unbalance of other subsystems and even of all the system as a whole.

Consideration was given to a numerical example of the optimal motion control of two-machine power system.

1 INTRODUCTION

The mathematical model of the modern electric power

complex, consisting of turbine generators and com-

plex multiply-connected energy blocks, is a system of

nonlinear ordinary differential equations. The opti-

mization problem, and the creation of algorithms for

constructing of controls by the principle of feedback

for such systems is actual and still attracts the atten-

tion of many researchers.

In this work while solving the problem of control

synthesis for the considered electric power system,

the constructions of the method of Bellman-Krotov

function in the form of necessary and sufﬁcient opti-

mality conditions were used (V. F. Krotov, 1996)–(V.

I. Gurman, 1997).

2 STATEMENT OF THE

PROBLEM

It is required to minimize the functional

J(u) = 0.5

∑

i=1



+ r



exp{γ

t}dt+

+Λ(x(T), y(T)),

(1)

under the conditions:

= y

= −λ

− f

(x) + b

) = x

, y

) = y

, i = 1, l, t ∈ (t

, T) (2)

x(t), y(t) : (t

, T) → R

where u

∈ R is scalar control; f

(x) is a continuously

differentiable scalar function satisfying the integrabil-

ity condition:

∂f

(x)

∂x

∂f

(x)

∂x

, ∀i 6= k; (3)

moments of time t

, T are assumed to be given;

, γ

, λ

are positive constants, k

(t) are positive func-

tions and the terminal value of x(T) , y(T) are un-

known beforehand.

It should be noted that if inequalities took place

< 0, i = 1, 2, . . . .l, then these coefﬁcients would

reﬂect the fact of discounting (playing the important

role in economical problems). In our case, these co-

efﬁcients are positive,that, naturally, imposes in con-

trol problem(1)–(3) additional requirements on the

condition function x

), y

), i = 1, 2, . .. , l,

and control u

(t), i = 1, 2, . . . , l, so that they in

view of weight coefﬁcients k

(t), r

, i = 1, 2, . . . , l,

decreased faster than the exponent exp{γ

t} , i =

1, 2. . . , l, and also provided deﬁniteness of integral

(1). It becomes essentially important obviously when

time T is great enough.

As it is known, in many, including complex, tech-

nical devices, ”danger” of deviations of controlled

system from a normal natural operating regime in

time does not decrease, and can only grow. The of-

fered quality functional (1) allows, ﬁrst, to struggle

with the speciﬁed ”danger” promptly and efﬁciently.

Second, after return of the system to the normal op-

erating regime of work it provides disappearance of

control inﬂuences as soon as possible.

The problem of synthesis for the Cauchy problem

(1)–(3) is very important for the problems of electric

186

Kalimoldayev M., Jenaliyev M., Abdildayeva A. and Kopbosyn L..

The Optimal Control Problems of Nonlinear Systems.

DOI: 10.5220/0005537701860190

In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 186-190

ISBN: 978-989-758-122-9

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

power systems work optimization.

2.1 The Main Lemma

Following to the Bellman-Krotov formalism (V. F.

Krotov, 1996)–(V. I. Gurman, 1997), we will show

the correctness of the following lemma.

Lemma. In order to provide the optimal control

of u

) = −

exp{−γ

t} y

, i =

1, l and the corre-

sponding solution of the system (2)–(3) {x(t), y(t)},

it is necessary and sufﬁcient that

K(x(T) , y(T)) = Λ(x(T),y(T)),

(t) = 2λ

exp{−γ

t} +

exp{−2γ

t} > 0,

i ∈

1, l,

(4)

K (x, y) = 0.5

∑

i=1

−

∑

i=1,

=0,

j>i

, . . . ,x

i−1

, ξ

, x

i+1

, .., x

)dξ

is the Bellman-Krotov function and besides,





= min

J(u) = K(x(t

), y(t

)).

2.2 Proof

For continuously differentiable function K (x, y) func-

tional (1) has the view:

J(u) = J(x(t) , y(t), u(t)) =

R[x(t) , y(t), u(t)]dt+

+ m

(x(T), y(T)) + m

(x(t

), y(t

)),

(5)

where

R[x, y, u] =

∑

i=1

+ K

(−λ

− f

(x) + b



+ r



exp{γ

t} ,

(6)

(x, y) = −K (x, y) + Λ(x, y),

(x, y) = K (x, y),

(7)

∂K

∂x

, K

∂K

∂y

, i =

1, l.

To ﬁnd the Bellman-Krotov function K(x, y) we use

the Cauchy problem:

(

inf

R[x, y, u] = 0, t ∈ (t

, T),

K(x(T) , y(T)) = Λ(x(T),y(T)).

(8)

Assuming that

= K

(x), K

= y

= f

(x), i =

1, l.

(9)

Taking into account (9), from (8) we obtain:

) = −

exp{−γ

t} y

(t) = 2λ

exp{−γ

t} +

exp{−2γ

t} > 0,

> 0, i ∈

1, l.

(10)

By virtue of integrability conditions of (3) and

the assumptions (9) we get the representation of the

Bellman-Krotov function (4).

From (8) it also follows that the value of the ter-

minal term of the functional (1) is deﬁned by:

Λ(x(T) , y(T)) = K(x(T), y(T)).

By virtue of the representations (6)–(7) along the

optimal control (10) the value of the functional J(u)

(1) will be equal:





= min

J(u) = K(x(t

), y(t

)).

To complete the proof of lemma, it remains only

to note that the existence of Bellman-Krotov function

in the form (4) provides not only the sufﬁciency of the

optimality conditions (8), but also their necessity.

3 THE OPTIMUM CONTROL

PROBLEM OF PHASE SYSTEM

Let us consider the problem of functional minimiza-

tion:

J(ν) = J(ν

. . . , ν

) = 0.5

∑

i=1



+ w



∗

∗ exp{γ

t} dt + Λ(δ(T), S(T)),

(11)

under the conditions:

dδ

= S

= −D

− f

(δ

) − N

(δ

) + ν

δ = (δ

, . . . ,δ

), S = (S

, . . . ,S

(12)

where w

, w

are weight coefﬁcients, correspond-

ingly positive functions and constants; H

is an iner-

tial constants; f

(δ

) are 2π-periodical continuously

differentiated functions; N

(δ) 2π-periodical con-

tinuous differentiated function srelative to δ

, . . . ,δ

;

TheOptimalControlProblemsofNonlinearSystems

187

for summands N

(δ)– the conditions of integrability

are carried out (3); T is duration of transient process

which is considered as speciﬁed.

The system of the equations (12) are supple-

mented with initial conditions

(0) = δ

, S

(0) = S

, i = 1, . . . , l. (13)

Terminal values δ(T), S(T) are beforehand un-

known, so they also should be determined.

The following theorem is valid.

Theorem 1. For optimization of controls

,t) = −[w

]

−1

exp{−γ

t}S

, i = 1, . . . , l,

and their corresponding solution



(t), S

(t)



system (12)–(13), it is necessary and sufﬁcient, that

Λ(δ(T), S(T)) = K(δ(T) , S(T)),

(t) = 2D

exp{−γ

t} + [w

]

−1

exp{−2γ

t} > 0,

i = 1, . . . , l,

where

K(δ, S) = 0.5

∑

i=1



(δ

)dδ



∑

i=1,

=0,

j>i

(δ

, . . . , δ

i−l

, δ

i+1

, . . . ,δ

)dξ

(14)

Bellman-Krotov function and besides,





= min

J(v) = K



, S



The proof of the theorem 1 is received, applying the

procedure of construction of Bellman-Krotov func-

tion suggested in 2 (see proof of lemma).

4 THE OPTIMAL CONTROL

PROBLEM OF POWER OF

STEAM TURBINES

One of the models describing the transients in the

electrical system is the following system of differen-

tial equations (I. I. Blekhman, 1997)–(A. A. Gorev,

2004):

dδ

= S

, H

= −D

− E

sinα

−

−P

sin(δ

− α

) −

∑

j=1, j6=i

sin(δ

− α

) + u

i ∈

1, l, t ∈ (0, T),

(15)

= δ

− δ

, P

= E

i,n+1

, P

= E

where δ

is an angle of rotor turn of i-th generator with

respect to some synchronous rotational axis (the axis

of rotation of bus-bares of constant voltage, which ro-

tates at the speed of 50 r./sec.; S

is sliding of i-th gen-

erator; H

is an inertial constant of the i-th machine; u

is mechanical power, which are led to the generator;

– EMF of the i-th machine; Y

– mutual conductiv-

ity of i-th and j-th branches of the system; U = const

is bus-bar voltage of constant voltage; Y

i,n+1

–deﬁnes

the bond (conductivity) of i-th generator with bus-bar

of constant voltage; D

= const ≥ 0 is mechanical

damping; α

, α

are constant values which take into

account the inﬂuence of active resistance in the stator

chains of generators.

The complexity of the analysis of the model (15)

is taking into account of α

, α

= α

. Since in this

case δ

= −δ

, then the model (15) is not conserva-

tive; one fails to build the Lyapunov’s function in the

form of the ﬁrst integral for it. The system is called

positional model.

Let the state variables and control variables in the

steady after-emergency regime be equal to:

= 0, δ

= δ

, u

= u

, i = 1, l. (16)

To obtain the system of the disturbed movement we

should proceed to the equations of deviations assum-

ing:

= ∆S

, δ

= δ

+ ∆δ

= u

+ ∆u

, i =

1, l.

(17)

Further, for the convenience we denote again the vari-

ables ∆u

, ∆δ

, ∆S

by u

, δ

, S

and from (15),(16)

we obtain:

dδ

= S

[−D

− f

(δ

) − N

(δ) + M

(δ) + u

i =

1, l, t ∈ (0, T),

(18)

where

(δ

) = P



sin



+ δ

− α



− sin



− α



(δ) =

∑

j=1, j6=i

(δ

, . . . ,δ

) =

∑

j=1, j6=i



sin



+ δ



− sinδ



(δ) =

∑

j=1, j6=i

(δ

, . . . ,δ

) =

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

188

= Γ



cos



+ δ



− cosδ



= P

cosα

, Γ

= P

sinα

, P

= P

= Γ

, k = 1, 2.

The control will be searched in the form of:

= ν

− M

(δ), i =

1, l, (19)

where the function ν

should be determined.

It is required to minimize the functional

J(ν) = J(ν

, . . . ,ν

) =

= 0.5

∑

i=1



+ w



∗

∗exp{γ

t}dt + Λ(δ(T), S(T)),

(20)

under the conditions (18)–(19), where w

, w

are

weight coefﬁcients, correspondingly positive func-

tions and constants; f

(δ

) is 2π-periodic continu-

ously differentiable function; N

(δ)2π-periodic con-

tinuously differentiable function with respect to δ

;

for N

(δ) the integrability condition of the type (3) is

realized; T is duration of the transition process which

is considered to be given. In addition, the initial con-

ditions are given:

(0) = δ

, S

(0) = S

, i =

1, l, (21)

and the values δ

(T) , S

(T) are unknown.

On the basis of the lemma from 2 we obtain

Theorem 2. In order to optimal control

,t) = − [w

]

−1

exp{−γ

t}S

, i =

1, l,

and the corresponding solution



(t), S

(t)



of sys-

tem (18), (20) it is necessary and sufﬁcient that

Λ(δ(T), S(T)) = K (δ(T), S(T)),

(t) = 2D

exp{−γ

t} + [w

]

−1

exp{−2γ

t} > 0,

i =

1, l,

K(δ, S) = 0.5

∑

i=1



(δ

)dδ



∑

i=1,

=0,

j>i

(δ

, . . . ,δ

i−l

, ξ

, δ

i+1

, . . . ,δ

)dξ

Bellman-Krotov function, and besides,





= min

J(ν) = K



, S



. (22)

It should be noted that in the proof of the theorem

2, assumptions (9) from the lemma take the form:

[ f

(δ

) + N

(δ)], (23)

i.e.

= H

, K

= f

(δ

) + N

(δ), i =

1, l.

5 THE NUMERICAL EXAMPLE.

OPTIMAL CONTROL OF THE

MOVEMENT OF

TWO-MACHINE ELECTRIC

POWER SYSTEM

In the system (15) we accept that i = 1, 2, and as-

sume that the mechanical damping is absent, i.e., co-

efﬁcients D

, D

are equal to zero. According to the

relations (15)–(21) the optimal control problem takes

the form (I. I. Blekhman, 2004):

J(ν) = J(ν

, ν

) = 0.5

∑

i=1



+ 0.1ν



∗

∗exp{γ

t}dt + 0.5



(T) + S

(T)



(24)

dδ

= S

[− f

(δ

) − N

(δ) + ν

i = 1, 2,

(25)

where

(δ

) = P



sin



+ δ

− α



− sin



− α



, i= 1 2,

(δ) = Γ



sin



+ δ



− sinδ



(δ) = Γ



cos



+ δ



− cosδ



= δ

− δ

= P

cosα

, Γ

= P

sinα

= δ

− δ

, δ

= −δ

The numerical data of the system (25):

= γ

= 0.1;

= −0.052; α

= −0.104;

= 2135; H

= 1256; P

= 0.85;

= 0.69; P

= 0.9;

= 0.827; δ

= 0.828, α

= −0.078;

and the initial data:

(0) = 0.18; δ

(0) = 0.1;

(0) = 0.001; S

(0) = 0.002.

(26)

According to formula (22) Bellman-Krotov func-

tion and its partial derivatives will have the form:

K(δ, S) ≈ 1067.5S

+628S

+2.004−cos(δ

+ 0.879)−

−0.77δ

− cos(δ

+ 0.932)− 0.83δ

(δ, S) = 0.425[sin(δ

+ 0.879)− sin0.879]+

+0.9sin(δ

− δ

(δ, S) = 0.345[sin(δ

+ 0.932)− sin0.932]+

+0.9sin(δ

− δ

TheOptimalControlProblemsofNonlinearSystems

189

(δ, S) = 2135S

, K

(δ, S) = 1256S

Controls on the feedback principle (synthesis) are

determined by the formulas:

(δ, S) = − exp{−0.1t}S

(27)

herewith the assumption was used (23). The re-

sults of numerical calculation of the optimal pair of

vector-functions state-control { δ

(t), S

(t); ν

(t) =



(t), S

(t)



the obtained from (25)–(27), as

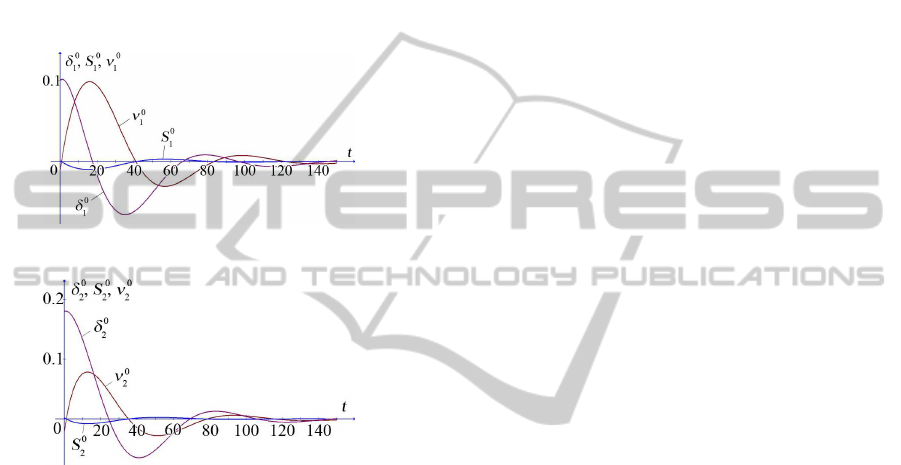
shown on the Figures 1 and 2.

Figure 1.

Figure 2.

6 CONCLUSIONS

On the basis of the theoretical results, the computa-

tional experimentswere conducted, which showed the

sufﬁcient efﬁcacy of the proposed procedure for con-

structing the function of Bellman-Krotov and the syn-

thesising optimal control for the given power system.

ACKNOWLEDGEMENTS

This work is partially supported by Grant

No.0925/GF1 of a Science Committee of the

Ministry of Education and Science of the Republic of

Kazakhstan.

REFERENCES

A. A. Gorev (2004). Transient processes of the synchronous

machine. M. Fizmatlit.

I. I. Blekhman (1997). Expansion principle in problems of

control. M. Fizmatlit.

I. I. Blekhman, A. (2004). On general deﬁnitions of syn-

chronization. In Selected topics in vibrational me-

chanics. World Scientiﬁc.

V. F. Krotov (1996). Global methods in optimal control

theory. M.Dekker.

V. I. Gurman (1997). Expansion principle in problems of

control. M. Fizmatlit.

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

190