
Reduction and Push Technology of Cable Harness Information for
Complex Mechatronic Products based on Variable Precision Rough
Sets
Falin Wang
1
, Wenhe Liao
1
, Yu Guo
1
and Xiaofei Wang
2
1
College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics
No. 29 Yudao Street, Qinhuai District, Nanjing City, 210016, Jiangsu Province, China
2
Nanjing Research Institute of Electronics Technology, No.8, Guorui Road, Yuhuatai District, Nanjing City 210039,
Jiangsu Province, China
Keywords: Cable Harness Information, Complex Mechatronic Products, Information Reduction, Information Push.
Abstract: As energy and signal transmission medium, cable harness is widely used in complex mechatronic products,
and cable harness information are the basis and premise conditions of the flexible cable harness assembly
simulation of complex mechatronic products system. To retrieve cable harness information from the
information management system or repository effectively, a push method of cable harness information for
complex mechatronic products based on variable precision rough sets (VPRS) was proposed in this paper.
By using the cable harness information reduction method, the cable harness information repository is
simplified, and rules which can support the precise push also be distilled from the reduct cable harness
information repository. On the basis of the above approach, cable harness wiring designers, assembly
process planners and assembly process simulation designers can efficiently share cable harness information
during all design processes. Finally, a case is employed to validate the proposed method of this paper.
1 INTRODUCTION
Complex mechatronic products like aerospace
vehicles, satellites, aircraft engine, rocket engine,
missile and automobile are the complex systems,
which composed of mechanical structures, electrical
equipments, control equipments, detect equipments
(Zhong, 2007), etc. Involved in many disciplinary,
complex manufacturing processes, more test links,
and long development cycle are the main
characteristics of those products. Developing
complex mechatronic products requires intensive
collaboration between engineers of the mechanical,
electronic, control, and software domains in a design
team (Bolón-Canedo et al., 2013, Wang et al., 2002,
M, 2002). Moreover, the complex mechatronic
products design is a typical information or
knowledge-intensive process, and involved in
complicated interactions among multidisciplinary
design teams in a distributed, heterogeneous and
dynamic environment, including cooperation,
coordination, and communication(Chen et al., 2008,
Shen et al., 2000).
As energy and signal transmission medium,
cable harness is widely used in complex mechatronic
products in fields such as aviation, aerospace,
automobile and shipbuilding industry, it is the “link”
between electrical equipments and every extension
module, the quality of the cable harness wiring has
become an important indicator to treasure overall
performance and reliability of products (Ning et al.,
2009, Shang et al., 2012).
In engineering applications, the cable harness has
a complex topology structure covering a lot of
geometric topology information, engineering
semantic information, management attribute
information, physical attribute information, cable
harness material information, cable harness auxiliary
material information, electrical connector
information, electrical function information and
decentralized wiring information, et al. Each class of
the above information contains additional sub-
information, such as physical attribute information
of cable harness contains cable harness weight, cable
harness density, bending property, tensile property
and minimum bending radius, et al.
As is well know, enterprises often occurring
263
Wang F., Liao W., Guo Y. and Wang X..
Reduction and Push Technology of Cable Harness Information for Complex Mechatronic Products based on Variable Precision Rough Sets.
DOI: 10.5220/0005538002630270
In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),
pages 263-270
ISBN: 978-989-758-120-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
“massive information” and “information flood”
phenomenon frequently due to the increasing of
cable harness wiring information, and some
information in the repository are redundant and not
important for the designers. Consequently, designers
spent more and more time to retrieve information
from the information management system, and even
difficult to retrieve information that meets the design
requirements, which are adverse to the cable harness
wiring design information sharing and reuse, and
also hindered improvement design efficiency and
level of the designers (Ji et al., 2013). How to
manage the existing cable harness wiring design
information effectively and extract guiding
significant rules accurately from the vast amounts of
cable harness wiring design information have
become the key point for enterprises to improve
complex mechatronic products development speed
and shorten the development cycle.
Information reduction of cable harness is one of
the processing techniques, and different methods and
tools have been proposed for effective and efficient
reduction of information (Farahat et al., 2013, Dai et
al., 2013, Ramentol et al., 2012, G et al., 2007). The
aim of reduction is to find a minimal attribute subset
of the original datasets that is the most informative,
and all other attributes can be deleted from the
databases with the minimal information loss. Then,
on this base, implement the right cable harness
wiring designer with the right information in the
right place at the right time and at the right cost(Li
and Yin, 2009, Naeve, 2005), that is realize the
precise information pushing.
2 CABLE HARNESS
INFORMATION MODEL AND
COLLABORATIVE DESIGN
WORK MODEL
2.1 Cable Harness Information Model
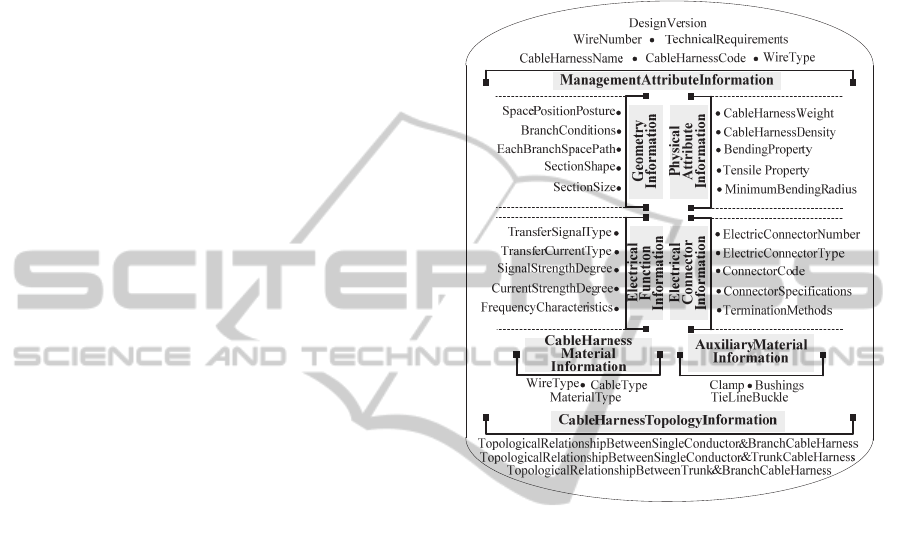
The cable harness information model (as shown in
Figure 1) mainly describes the relevant information
of cable harness properties, such as cable harness
geometry information, cable harness physical
attribute information, cable harness topology
information, cable harness electrical functional
information, etc.; each kind of information
represents the actual working state information
content of cable harness.
In the assembly simulation of complex
mechatronic products system of flexible cable
harness, wiring design determines the assembly
process, assembly process is the basis of assembly
process simulation, while cable harness information
model is the basis and premise conditions of the
above works, and also is the data source which
required for each above phase.
Figure 1: Cable harness information model of complex
mechatronic products.
2.2 Collaborative Design Work Model
In this paper, we have built a collaborative design
work model for complex mechatronic products, and
shown in Figure 2. In this model, we transform the
collaborative design task into a whole problem
solving task. By applying the task decomposition
method and principle, the whole problem solving
task will be decomposed into several
subtasks:
12
,,,
n
TT T
; then allocate these subtasks to
the multi-design teams which are set up on the basis
of common consensus, trust, and cooperation. Each
design team solve its own subtask and composite all
the sub solutions ultimately.
The collaborative design work model established
in this paper mainly composed of three layers (as
shown in Figure 2.): management layer of design
organization, management layer of design task and
management layer of design activity. The detail
description of each layer as follows.
(1) Management Layer of Design Organization:
to complete the task and realize the goal of the
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
264

organization, the project manager must develop a
practical and effective form of organization structure
according to the situation of the enterprise and the
project itself combine each subsystems design
experts, designer, analyst, and other participants.
(2) Management Layer of Design Task: the main
responsibility of this layer is to determine the overall
goals and tasks of the product design, and
decompose the overall tasks into a series of subtasks
combine relevant decomposition principles. The
reasonable allocation of those subtasks also finished
in this layer.
(3) Management Layer of Design Activity: in this
layer, each collaborative design team completes the
allocated subtask on the collaborative work
platform, and implement the task that pushes the
design information to the designer in accordance
with certain design rules. During the whole design
process, collaborative design teams will share and
reuse the design information or resources in real
time among each other.
Collaborative work platform is the basic
foundation for the complex mechatronic products
design; it has the necessary hardware and software
environment, and also includes the design
specifications, resource library and information or
knowledge base, covering multiple aspects of the
personnel organization, resource allocation, process
management and design results concentration, etc.
The designers can share the product data material
and design resources through the collaborative work
platform, and thereby discuss and modify the design
solutions.
3 CABLE HARNESS
INFORMATION REDUCTION
AND PUSH METHOD
The variable precision rough sets model (VPRS),
firstly proposed by Ziarko (W., 1993), is an effective
mathematical tool with an error-tolerance capability
to handle uncertainty problem. Basically, the VPRS
2
T
n
T
1
T
Figure 2: Collaborative design work model for complex mechatronic products.
ReductionandPushTechnologyofCableHarnessInformationforComplexMechatronicProductsbasedonVariable
PrecisionRoughSets
265

is an extension of Pawlak’s rough set theory
(Pawlak, 1991, Pawlak, 1982), allowing for partial
classification. By setting a confidence threshold
value
, the VPRS cannot only solve classification
problems with uncertain data and no functional
relationship between attributes, but also relax the
rigid boundary definition of Pawlak’s rough set
model to improve the model suitability. Due to the
existence of
, the VPRS can resist data noise or
remove data errors (Śle¸zak and Ziarko, 2005). In
this paper, we use the approach of VPRS to
implement cable harness information reduction and
push.
3.1 Roughening Description of Cable
Harness Information Push based on
VPRS
In this section, we introduce the roughening
description method of cable harness information
push based on VPRS, and briefly review some
notions related with VPRS which can be found in
(Ye et al., 2014, Li and Yin, 2009, Mi et al., 2004,
GY, 2001, W, 1993).
In form, a quadruple
,,,SUAVf
is an
information system (or called a cable harness
information push decision system). Where,
12
{, , , }
n
Uxx x
is a non-empty finite set of
objects called the universe; each object of universe
U
represents a case of design (or browsing history
of cable harness information) in complex
mechatronic products design process.
A
is a non-
empty finite set of attributes, and
A
CD
;
where
C
represents condition attribute set,
{}
D
d
is
decision attribute set,
CD
; here, we let the
condition attribute set
C
as the cable harness
information attribute, and let the decision attribute
set
{}
D
d
as the design proposal that the designer
will be referenced in a new product development
task. An attribute can be defined as
:
a
aU V
for
every
aA
, where
a
VV
and the set
a
V
is called
the value set of
a
.
:
f
UA V
is an information
function such as for any
aA and
x
U
,
,
a
f
xa V
.
f
defines the mapping
relationship between the cable harness information
and its attribute values.
Definition 1 (Indiscernibility Relation). Let
,,,SUAVf
be a cable harness information push
decision system, then with any
BA
there is
associated an equivalence relation:
2
() {(,) | (,) (,), }
A
IND B x y U f x a f y a a B
(1)
Where
()
A
I
ND B
is called the
B
indiscernibility
relation. The equivalence classes of the
B
indiscernibility relation are denoted
[]
B
x
or
()UINDB
, it can be abbreviated as
UB
.
Definition 2 (Lower Approximations and Upper
Approximations). Let
,,,SUAVf
be a cable
harness information push decision system and
let
,
X
UB A
, we can approximate
X
using
only the information contained in
B
by constructing
the
B
lower and
B
upper approximations of
X
,
denoted
()
B
RX
and
()
B
RX
respectively, where
( ) { |[] } {[]|[] }
BBBB
R
XxUx X xx X
(2)
and
( ) { |[] } {[]|[] }
BB BB
RX xU x X x x X
(3)
The lower approximation
()
B
RX
is the set of
objects that belong to
X
with certainty, while the
upper approximation
()
B
RX
is the set of objects that
possibly belong to
X
.
Definition 3 (Consistent and Inconsistent Cable
Harness Information Push Decision System). Let
,,,SUAVf
be a cable harness information push
decision system,
C
represents condition attribute set,
{}
D
d
represents decision attribute set, denote
equivalence relation:
{( , ) | ( ) ( ), }
Cijcicj
RxxfxfxcC
(4)
and
{( , ) | ( ) ( ), }
dijdidj
R
xx f x f x d D
(5)
If
Cd
R
R
, then
,,,SUCDVf
is called
consistent cable harness information push decision
system, otherwise it is called inconsistent cable
harness information push decision system.
Definition 4 (Discernibility Matrix of Consistent
Decision System). Let
,,,SUAVf
be a cable
harness information push decision system,
C
represents condition attribute set,
{}
D
d
represents decision attribute set, denote:
{[ ] | }
CiCi
UR x x U
(6)
{[ ] | }
didi
UR x x U
(7)
and
([ ] ,[ ] ) { | ( ) ( )}
diC jC k ki kj
D
x x a Cfx fx
(8)
Where,
[] [ ]
id jd
xx
. When
[] []
id jd
xx
,
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
266

([ ] ,[ ] )
diCjC
Dx x
, then
([ ] ,[ ] )
diCjC
Dx x
is
called decision discernibility set about
[]
iC
x
and
[]
jC
x
, while,
(([],[])|[],[] )
diCjC iCjC C
D
Matrix D x x x x U R
(9)
is called the discernibility matrix of consistent
decision system.
Definition 5 (Probability Distribution Function).
Let
,,,SUAVf
be a cable harness information
push decision system and
B
C
. Denote:
{( , ) | ( ) ( ), }
Bijkikjk
R
xx f x f x c B
(10)
and
{[ ] | }
BiBi
UR x x U
(11)
12
{, , , }
dr
UR PP P
(12)
Where,
[] { |(, ) }
iB j i j B
x
xxx R
. For
,
i
x
U
let
( []) [] [],( )
jiB j iB iB
PP x P x x j r
, then,
define
12
() (( []),( []), ,( []))
B i iB iB r iB
xPPxPPx PPx
(13)
is the probability distribution functions of the
d
UR
.
Definition 6 (
Lower and Upper Approximations).
Let
,,,SUAVf
be an inconsistent cable harness
information push decision system.
Let
(0.5,1]
,
A
CD
,
B
C
, for
XU
,
denote:
(){ |( [] }
Bi iB
RX x UPXx
{[ ] | ( [ ] }
iB iB
xPXx
(14)
(){ |( [])1 }
Bi iB
RX x UPXx
{[ ] | ( [ ] ) 1 }
iB iB
xPXx
(15)
()
B
RX
and
()
B
R
X
are called
lower
approximation and
upper approximation,
respectively. Where
()PXY X Y Y
if
0Y
,
and
()1PXY
otherwise.
X
is the cardinality of
the set
X
.
Definition 7 (
Upper and Lower Distribution
discernibility matrices). Let
,,,SUCDVf
be
an inconsistent cable harness information push
decision system.
12
{, , , }
Cm
UR CC C
. Denote:
*
1
{([ ] ,[ ] ) | ( ) ( )}
CC C C
D
xy MxMy
(16)
*
2
{([ ] ,[ ] ) | ( ) ( )}
CCC C
DxyGxGy
(17)
Where,
() { | ( )},
C
Cj j
M
xPxRPxU
;
() { | ( )},
C
Cj j
Gx PxRP xU
. Denoted by
(,)
ik
f
Ca
the value of
k
a
about the objects in
i
C
.
Define
(, )
lij
DCC
{|(,)(,)},
kikjk
aCfCa fCa
*
(, ) ,
ij l
CC D
*
(, ) ,
ij l
CC D
1, 2.l
,C
(18)
then
1
(, )
ij
DCC
and
2
(, )
ij
DCC
are the
upper and
lower distribution discernibility attribute sets
respectively. Here, we denote:
11
((,)|, )
ij
DMatrix D C C i j m
(19)
and
22
((,)|, )
ij
DMatrix D C C i j m
(20)
and they are called
upper and lower distribution
discernibility matrices respectively in the cable
harness information push decision system.
Definition 8 (Decision Matrix). Let
,,,SUCDVf
be a cable harness information
push decision system,
() , ,, ,
B
SB U B DV f
(0.5,1]
is an attribute reduction decision table after
attribute reduction. Let
(1,2,,)
i
Xi p
and
(1,2,,)
j
X
jq
represent the equivalence class of
the relation
()
RB
. Where,
(),
iBrj
XPosPX
()
B
r
Neg P
, then, define the decision matrix
( ) ( 1,2, , ; 1,2, , )
ij p q
M
ci pj q
(21)
as
{( , ( , )) | , ( , ) ( , )}
ij i i j
cafXaaBfXafXa
(22)
Given an equivalence class
i
X
, take each element of
M
as a Boolean expression, then the decision rule
sets can be expressed as the following Boolean
function
i
()
ij
c
ij
c
(23)
Hence, we can calculate the minimal disjunctive
normal form, and get the rule sets of
r
P
. The rule’s
support can also be calculated out.
3.2 Rules Generate and Cable Harness
Information Push Method based on
VPRS
Rule extraction is one of the major forms of data
ReductionandPushTechnologyofCableHarnessInformationforComplexMechatronicProductsbasedonVariable
PrecisionRoughSets
267

mining and is perhaps the most common form of
cable harness information discovery in cable harness
information push decision systems (Li et al., 2013,
Fan et al., 2005, Mi et al., 2004). To implement rules
extraction, two definitions will be given firstly.
Definition 9 (decision rule). Given a decision table:
,,,SUCDVf
. Let
(),XUINDC
(),YUINDD
,
x
X
() (,())
C
cC
des X c c x
(24)
represents the description of the equivalence
class
X
;
,yY
() (,())
D
dD
des Y d d x
(25)
represents the description of the equivalence class
Y
.
Define
:() (),
CD
r des X des Y Y X
(26)
is the decision rule from
X
to
Y
.
Definition 10 (support of rule r). Let
,,,SUCDVf
be a cable harness information
push decision system,
U
is called the universe. For
each rule
:() ()
Ci Dj
rdes X des Y
, the support can be
defined as:
()
ij
Sup r X Y U
(27)
4 CASE STUDY
To implement the cable harness information push,
we designed a decision table like Table 2, and the
meaning of each symbol represents can see in Table
1.
Table 1: The meaning of each symbol represents.
Symbol Meaning Symbol Meaning
1
a
stray electromag-
netic field
1
capacitance
weakness
2
a
cable harness
insulation strength
2 capacitance strong
3
a
degree of coupling
crosstalk
3
low degree of
coupling crosstalk
4
a
distributed capacita
n-ce
4
general degree of
coupling crosstalk
d
wiring quality of
cable harness
5
high degree of
coupling crosstalk
1
Q
high quality 6
300M
2
Q
general quality 7
100 300M
3
Q
low quality 8
100M
Table 2: Decision table of cable harness information push.
U
C
D
1
a
2
a
3
a
4
a
d
1
x
1 4 5 8
1
Q
2
x
2 3 6 7
2
Q
3
x
1 4 6 8
3
Q
4
x
2 3 5 7
3
Q
5
x
1 4 6 8
3
Q
6
x
1 4 6 8
2
Q
7
x
1 4 5 8
1
Q
8
x
2 3 6 7
2
Q
According to the equivalence relation
C
R
and
D
R
on
U
, Let
11 17
[] {, },
A
Cx xx
22 28
[] {,},
A
Cx xx
33 356
[] {,,},
A
Cx xxx
44 4
[] {}.
A
Cx x
11 17
[] {, },
D
D
xxx
22 268
[] {,,},
D
D
xxxx
33 345
[] {,,}.
D
D
xxxx
The partitions on the universe
U
generated by
the equivalence relation
C
R
and
D
R
are
1234
{, , , },
C
UR CC C C
123
{, , }.
D
UR DD D
Due
to
AD
RR
, the Table 2 is an inconsistent cable
harness information push decision table according to
the definition 3. Then we use the processing method
for the inconsistent decision table to calculate the
probability distribution functions on the equivalence
class
C
UR
, and the results are
17
( ) ( ) (1,0,0)
AA
xx
,
28
() ()(0,1,0)
AA
xx
,
356
() () () (0,13,23)
AAA
xxx
,
4
()(0,0,1)
A
x
.
When the classification error
0.7
, the upper
approximation set of the set
1
D
,
2
D
and
3
D
about
the relation
R
are as follows respectively:
0.7
117
(){,},
A
R
Dxx
0.7
223568
(){,,,,},
A
RD xxxxx
0.7
33456
(){,,,}
A
RD xxxx
.
So we have
0.7 0.7
171
() (){},
AA
M
xMx D
0.7 0.7
282
() (){},
AA
M
xMx D
0.7 0.7 0.7
35623
() () (){ , },
AAA
M
xMxMx DD
0.7
43
(){}
A
M
xD
.
And the decision discernibility set is
*0.7
1 121314232434
{(,),(,),(,),(,),(,),(,)}D CCCCCCCCCCCC
.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
268

Because
0.7
1 1 2 1234
(, ){,,,},
D
CC aa aa
0.7
113 3
(, ){},DCC a
0.7
114 124
(, ){,,},
D
CC aa a
0.7
123 124
(,){,,},
D
CC aaa
0.7
124 3
(,){},
D
CC a
0.7
134 1234
(, ){,,,}
D
CC aaaa
.
So we construct the upper approximation
discernibility matrix is (
0.7
):
1234
1234 1234
0.7
1
31241234
124 3 1234 1234
{, , , }
{, , , }{, , , }
.
{} {, , } {, , , }
{,,} {} {,,,}{,,,}
aaaa
aaaa aaaa
DMatrix
aaaaaaaa
aaa a aaaa aaaa
and the upper distribution discernibility formula we
solve is
0.7
1 1234 124 3
()()
M
aaaa aa a a
13 23 34
()()().aa aa aa
From the upper distribution discernibility formula,
we know that the attribute sets
13
{, }aa
,
23
{,}aa
and
34
{, }aa
are the three distribution reduction of the
cable harness information push system (here,
accuracy is 0.7), and the attribute
3
a
is core
attribute.
To obtain the push rule sets of cable harness
information, we must construct the decision matrixes
of the set
1
D
,
2
D
and
3
D
. Select a set
13
{, }
B
R
ED a a
from the attribute reduction sets, and
its equivalence class can be denoted
as
1234
{, , , }
B
U RED C C C C
. The discernibility
matrices we solved for
1
D
,
2
D
and
3
D
are shown in
Table 3, Table 4 and Table 5.
Table 3: Discernibility matrix of decision
1
D
.
2
C
3
C
4
C
1
(,1)a
3
(,5)a
1
(,1)a
1
C
3
(,5)a
Table 4: Discernibility matrix of decision
2
D
.
1
C
3
C
4
C
1
(,2)a
1
(,2)a
3
(,6)a
2
C
3
(,6)a
Table 5: Discernibility matrix of decision
3
D
.
1
C
2
C
3
C
1
(,2)a
3
(,5)a
1
(,2)a
4
C
3
(,5)a
Table 6: Push rule sets and supports.
Rules Supports (%)
11 3 1
:( 1) ( 5) ( )ra a dQ
25
21 3 2
:( 2) ( 6) ( )ra a dQ
25
31 3 3
:( 2) ( 5) ( )ra a dQ
12.5
On the basis of discernibility matrices, the minimum
disjunctive normal form (DNF) of the Table 3, Table
4 and Table 5 can be expressed as follows:
1113 3131
()((1)(5))(5)(1)(5)(1).BDaa aaaa
1213 1313
( ) (( 2) ( 6)) ( 2) ( 6) ( 2) ( 6).BDaa aa aa
1313 13 13
( ) ( 2) ( 5) (( 2) ( 5)) ( 2) ( 5).BDaa aa aa
To sum up the above analysis, the push rule sets and
its supports of the cable harness information are
express at the Table 6. The support size of the cable
harness information rules reflects the degree of
information which the designers used. For all cable
harness information push rule sets, low support rules
should be eliminated. In practice, we can set a
threshold of support (e.g. 15%), support is less than
the threshold will be eliminated, and push the cable
harness information to designers will be more
accurately.
5 CONCLUSIONS
This research focuses on the techniques of cable
harness information reduction and push. By using
those techniques, the design repository is simplified
and we can extract rules which can support the
precise push of cable harness information. And the
methods or techniques proposed in this paper will
play an important role in the field of flexible cable
harness assembly simulation for complex
mechatronic products. Though significant progress
has been made on cable harness information
reduction and push, there is still much work to be
conducted in the future, such as ontology modelling
and representation of cable harness information,
evaluation of the effect of a cable harness
information push, among others.
ReductionandPushTechnologyofCableHarnessInformationforComplexMechatronicProductsbasedonVariable
PrecisionRoughSets
269

ACKNOWLEDGEMENTS
This research work was supported by Funding of
Jiangsu Innovation Program for Graduate Education
and the Fundamental Research Funds for the Central
Universities (Grant no. KYLX_0311).
REFERENCES
Bol N-Canedo, V., S Nchez-Maro O, N. & Alonso-
Betanzos, A. 2013. A Review of Feature Selection
Methods on Synthetic Data. Knowledge and
Information Systems, 34, 483-519.
Chen, Y.-J., Chen, Y.-M. & Chu, H.-C. 2008. Enabling
Collaborative Product Design through Distributed
Engineering Knowledge Management. Computers in
Industry, 59, 395-409.
Dai, J., Wang, W., Tian, H. & Liu, L. 2013. Attribute
Selection Based On A New Conditional Entropy For
Incomplete Decision Systems. Knowledge-Based
Systems, 39, 207-213.
Fan, Z.-P., Feng, Y. & Sun, Y.-H. 2005. A Framework On
Compound Knowledge Push System Oriented To
Organizational Employees, First International
Workshop, Internet And Network Economics.
Farahat, A., Ghodsi, A. & Kamel, M. 2013. Efficient
Greedy Feature Selection for Unsupervised Learning.
Knowledge and Information Systems, 35, 285–310.
G, P., W, B., J, F. & Kh, G. 2007. Engineering Design: A
Systematic Approach. 3rd Ed, London (UK), Springer
London Limited.
Gy, W. 2001. Rough Set Theory and Knowledge
Discovery, Xi’an, Xi’an Jiaotong University Press.
Ji, X., Gu, X. & Dai, F. 2013. Technology for Product
Design Knowledge Push Based On Ontology and
Rough Sets. Computer Integrated Manufacturing
Systems, 19, 7-20.
Li, F. & Yin, Y. 2009. Approaches To Knowledge
Reduction Of Covering Decision Systems Based On
Information Theory. Information Sciences, 179, 1694-
1704.
Li, J., Mei, C. & Lv, Y. 2013. Incomplete Decision
Contexts: Approximate Concept Construction, Rule
Acquisition And Knowledge Reduction. International
Journal of Approximate Reasoning, 54, 149-165.
M, T. 2002. Mechatronics: From the 20th to the 21st
Century. Control Eng Practice, 10, 877–86.
Mi, J.-S., Wu, W.-Z. & Zhang, W.-X. 2004. Approaches
To Knowledge Reduction Based On Variable
Precision Rough Set Model. Information Sciences, 159,
255-272.
Naeve, A. 2005. The Human Semantic Web Shifting From
Knowledge Push to Knowledge Pull. International
Journal on Semantic Web and Information Systems, 1,
1-30.
Ning, R., Liu, J., Tang, C. & Zhang, X. 2009. Virtual
Assembly Technology and Its Application. Defense
Manufacturing Technology, 4, 8.
Pawlak, Z. 1982. Rough Sets. International Journal of
Computer and Information Science, 11, 341–356.
Pawlak, Z. 1991. Rough Sets: Theoretical Aspects of
Reasoning about Data, Boston, Kluwer Academic
Publishers.
Ramentol, E., Caballero, Y., Bello, R. & Herrera, F. 2012.
Smote-Rsb*: A Hybrid Preprocessing Approach Based
On Oversampling And Under Sampling For High
Imbalanced Data-Sets Using Smote And Rough Sets
Theory. Knowledge and Information Systems, 33,
245–265.
Shang, W., Ning, R., Liu, J. & Wang, Z. 2012. Assembly
Process Simulation for Flexible Cable Harness in
Complex Electromechanical Products. Journal of
Computer-Aided Design & Computer Graphics, 24, 10.
Shen, W., Norrie, D. H. & Barthes, J. P. 2000. Multi-Agent
Systems for Concurrent Intelligent Design and
Manufacturing, London, Uk, Taylor & Francis.
Śle¸Zak, D. & Ziarko, W. 2005. The Investigation of the
Bayesian Rough Set Model. International Journal of
Approximate Reasoning, 40, 81-91.
W., Z. 1993. Variable Precision Rough Set Model.
Journal of Computer and System Sciences, 46, 39-59.
Wang, L., Shen, W., Xie, H., Neelamkavil, J. & Pardasani,
A. 2002. Collaborative Conceptual Design—State Of
the Art and Future Trends. Computer-Aided Design,
34, 981-996.
Ye, M., Wu, X., Hu, X. & Hu, D. 2014. Knowledge
Reduction For Decision Tables With Attribute Value
Taxonomies. Knowledge-Based Systems, 56, 68-78.
Zhong, J. 2007. Coupling Design Theory and Method of
Complex Electromechanical System, China Machine
Press, Beijing.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
270
