Numerical Integration of Multiple Integrals using Taylor Polynomial

Jan Chaloupka

, Ji

ı Kunovsk

, V

aclav

atek

1,2

, Petr Veigend

and Al

zbeta Martinkovi

cov

Faculty of Information Technology, Brno University Of Technology, Boz

echova 2, Brno, Czech Republic

IT4Innovations, V

SB Technical University of Ostrava, 17. listopadu 15/2172, 708 33 Ostrava-Poruba, Czech Republic

Keywords:

Multiple Integrals, Numerical Integration, Taylor Polynomial, Modern Taylor Series Method.

Abstract:

The paper concentrates on a new method of numerical computation of multiple integrals. Equations based

on Taylor polynomial are derived. Multiple integral of a continuous function of n-variables is numerically

integrated step by step by reducing its dimension. First, integration formulas for a function of two variables

are derived. Formulas for function of n-variables are generalized using composition. Numerical derivatives for

Taylor terms are repeatedly computed from simple integrals. Finally method is demonstrated on an exponential

function of two-variables and a new approach to determine a number of Taylor terms is discussed.

1 INTRODUCTION

The aim of this paper is to show a way how to nu-

merically integrate a function of n variables by trans-

forming the integral into a differential equation. Dif-

ferential equation is solved by Taylor polynomial

where higher derivatives are numerically computed

from simple integrals of previously solved differen-

tial equations.

To determine a number of Taylor terms for a gen-

eral function known only by its discrete points and to

achieve a given error is still an open problem. Upper

bound of an absolute value of all terms can be inves-

tigated. Optimal order approach to determine an inte-

gration step and a degree of Taylor polynomial (Jor-

dan, Maorong, 2005) and its modiﬁcation (Abad, Bar-

rio, Blesa, Rodriguez, 2012) can be found. In this pa-

per terms are computed by dot product of rows of an

inverse matrix and a vector of discrete points. Anal-

ysis of the product and partial approximation of the

bound is given.

2 DOUBLE INTEGRAL

Let’s have a double integral of general continuous

function

f (x,y)dx dy.

Translating f into origin, the equivalent integral

can be obtained.

−y

−x

(x,y)dx dy (1)

(x,y) = f (x

+ x,y

+ y) (2)

Without any loss of generality all double inte-

grals can be rewritten into the following form (lower

bounds are equal to zero).

f (x,y)dx dy (3)

Integration step for x-axis is denoted by h, for y-

axis by k, h =

, k =

, where p, resp. q are number

of partitions of x, resp. y axis.

2.1 Sampling by an Axis

Sampling the function f by y-axis, the following sys-

tem is obtained.

g(x,0) = f (x,0)

g(x,k) = f (x,k)

g(x,2k) = f (x,2k)

g(x, jk) = f (x, jk) (4)

g(x,qk) = f (x,qk)

From here on, g

(x) denotes g(x, jk).

163

Chaloupka J., Kunovský J., Šátek V., Veigend P. and Martinkovi

cová A..

Numerical Integration of Multiple Integrals using Taylor Polynomial.

DOI: 10.5220/0005539701630171

In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),

pages 163-171

ISBN: 978-989-758-120-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

−2

−1.5

−1

−0.5

0.5

1.5

0.2

0.4

0.6

0.8

0.2

0.4

0.6

0.8

1.2

1.4

1.6

(x)

f(x, y)

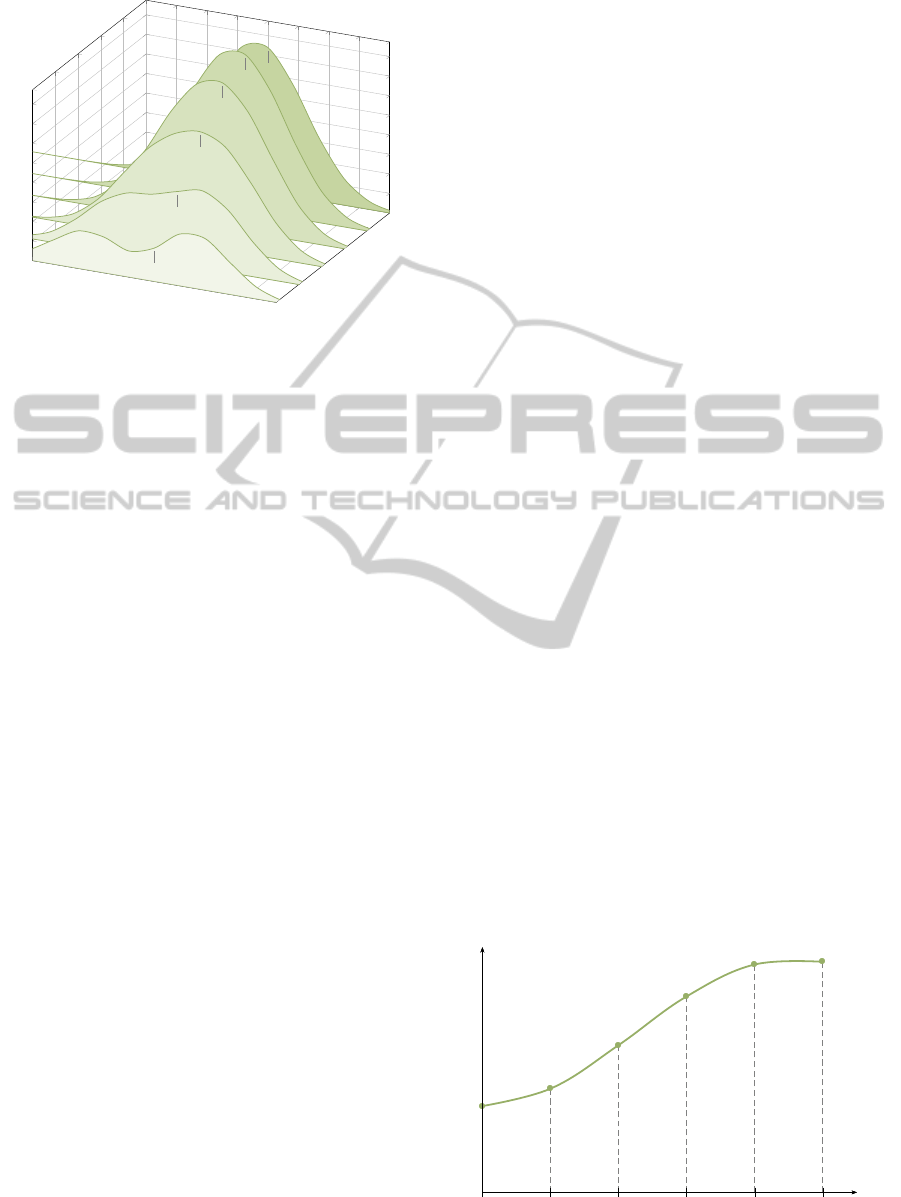
Figure 1: Graph of f(x,y).

2.2 First Integration

From the Figure 1.

(x)dx

(x)dx (5)

(x)dx

This system can be transformed into an equivalent

system of differential equations.

(t) = g

(t),I

(0) = 0

(t) = g

(t),I

(0) = 0

(t) = g

(t),I

(0) = 0 (6)

(t) = g

(t),I

(0) = 0

2.3 Numerical Solution of Differential

Equations using Taylor Polynomial

Taylor polynomial is used to approximate functions

(x) (system of equations (6)).

(h) = I

(0) +

∑

m=1

(m,0)

(2h) = I

(h) +

∑

m=1

(m,1)

(sh) = I

((s − 1)h) +

∑

m=1

(m,s − 1) (7)

(ph) = I

((p − 1)h) +

∑

m=1

(m, p − 1)

where j = 1..q, DI

(m,s) are members of Taylor

expansion, ∀ j : I

(0) = 0 (area starts from 0).

2.4 Sampled Integrals

New function ψ (Figure 2) can be created from solu-

tions of the system (7). Its domain consists of points

given as multiples of k.

ψ(0) = I

ψ(k) = I

ψ( jk) = I

(8)

ψ(qk) = I

Using ψ, double integral can be approximated us-

ing the following formula (supposing

ψ is continuous

version of ψ).

f (x, y)dx dy ≈

ψ(y)dy (9)

Figure 2: Graph of ψ(y).

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

164

Let’s denote integral (9) as function e.

e(y

) =

ψ(y)dy (10)

Now the process of differentiation can be re-

peated.

(t) = ψ(t) e(0) = 0 (11)

Again, function e can be solved using Taylor poly-

nomial.

e(k) = e(0) +

∑

m=1

(m)

(0)

e(2k) = e(k) +

∑

m=1

(m)

(k)

e( jk) = e(( j − 1)k) +

∑

m=1

(m)

(( j − 1)k)

(12)

e(qk) = e((q − 1)k) +

∑

m=1

(m)

((q − 1)k)

Using (11).

(m)

(t)

(m−1)

(t)

(13)

So the system of equations (12) can be rewritten.

e(k) = e(0) +

∑

m=1

(m−1)

(0)

e(2k) = e(k) +

∑

m=1

(m−1)

(k)

e( jk) = e(( j − 1)k) +

∑

m=1

(m−1)

(( j − 1)k)

(14)

e(qk) = e((q − 1)k) +

∑

m=1

(m−1)

((q − 1)k)

However, in this case the derivatives of ψ are

unknown, which means that a different approach is

needed. Let’s construct the following system,

ψ(k) = ψ(0)+

∑

m=1

Dψ(m,0)

ψ(2k) = ψ(0)+

∑

m=1

Dψ(m,0)

ψ( jk) = ψ(0)+

∑

m=1

Dψ(m,0) (15)

ψ(nk) = ψ(0)+

∑

m=1

Dψ(m,0)

where Dψ(m,t) =

(m)

(t)

Because ψ(y

+ jk) = I

, the system (15) is equivalent

to system (16).

∑

m=1

Dψ(m,0)

∑

m=1

Dψ(m,0)

∑

m=1

Dψ(m,0) (16)

∑

m=1

Dψ(m,0)

System can then be expressed in matrix form.

b =







− I

...

− I

...

− I







A =







1 1

... 1

2 2

... 2

...

j j

... j

...

n n

... n







x =







Dψ(1,0)

Dψ(2,0)

...

Dψ( j, 0)

...

Dψ(n,0)







NumericalIntegrationofMultipleIntegralsusingTaylorPolynomial

165

Putting it all together.

Ax = b (17)

Solving a vector x terms Dψ( j,0) are obtained.

These terms can be used to solve e(k) in system of

equations (14). The remaining e( jk) can be calculated

analogically, the matrix A stays the same, matrix b

needs to be recalculated for each e( jk).

Matrix A is ill-conditioned, multiple precision

arithmetic must be used for higher order. Block-

wise inversion and twelfth-order convergence numer-

ical method (Haghani and Soleymani, 2014) can be

used for inverse matrix computation.

3 MULTIPLE INTEGRAL

Generally, a multiple integral is in the following form.

...

f (x

,.. .,x

)dx

... dx

(18)

Translating function f to origin, equivalent inte-

gral is obtained.

−a

...

−a

g(x

,.. .,x

)dx

... dx

(19)

g(x

,.. .,x

) = f (a

+ x

,.. .,a

+ x

) (20)

3.1 Basic Deﬁnitions

Let N = {1, ... ,n}. Permutation from N to N is a

bijective function π : N → N. In order to eliminate an

ordering of integration steps in (19), permutation is

used.

π(n)

...

π(1)

g(x

,.. .,x

)dx

π(1)

... dx

π(n)

(21)

With no loss of generality, it can be written as fol-

lows.

...

g(x

,.. .,x

)dx

... dx

(22)

Further, isomorphism of composition of tuples

is implicitly taken, e.i. ((1,. .., n),(n + 1,. .. ,m)) ≈

(1,.. .,m). Integral’s bounds deﬁne a closed space

i∈N

h0,b

i. Integration step for i-th interval is de-

noted as h

, number of partitions as d

. Then h

3.2 First Integration

To simplify a notation of sampling.

,.. .,i

) = f (x

,.. .,i

) (23)

The deﬁnition of g

is derived from the the num-

ber of simple integrals after sampling (c = ×

i∈N

1)). The set of indexes has to be deﬁned.

Φ(x

) = Π

i∈N−{1,..., j}

{0,.. .,d

},1 ≤ j ≤ n (24)

To compute all c integrals, for each s ∈ Φ(x

= I

) =

,s)dx

(25)

Transformed into differential equation (initial

value problem).

(t) = g

(t,s), I

(0) = 0 (26)

Solving using Taylor polynomial

) = I

(0) +

α(s,1)

∑

m=1

(m)

(0)

(2h

) = I

) +

α(s,2)

∑

m=1

(m)

) (27)

) = I

) +

α(s,d

)

∑

m=1

(m)

)

where d

= d

−1 and α(s, j) stands for number of

members of Taylor polynomial for integral s in time

At the point d

) ≈

,s)dx

(28)

3.3 Composition

For each p ∈ Φ(x

) where

= (i, p), 0 ≤ i ≤ d

(29)

new function is obtained (analogy to double inte-

gral depicted in Figure 2).

Multiple integral can be approximated

...

f (x

,.. .,x

)dx

... dx

≈

...

,.. .,x

)dx

... dx

(30)

where

is a continuous version of ψ

,.. .,i

) = I

,s = (i

,.. .,i

) ∈ Φ(x

) (31)

Further

...

ψ(x

,.. .,x

)dx

... dx

...

,.. .,x

)dx

... dx

(32)

where

,.. .,t

) =

ψ(x

... ,t

)dx

(33)

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

166

3.4 Generalization

was deﬁned previously for s ∈ Φ(x

). This can be

generalized for p

∈ Φ(x

),2 ≤ k < n:

= I

) =

, p

)dx

(34)

, p

) = I

k−1

, p

k−1

= (d

e, p

) (35)

For integrals:

...

,.. .,x

)dx

... dx

...

k+1

,.. .,x

)dx

k+1

... dx

(36)

where

k+1

,.. .,t

) =

k+1

... ,t

)dx

(37)

,.. .,i

) = I

k−1

, p

k−1

= (i

,.. .,i

) (38)

Using formula (35) ψ

can be expressed as

,.. .,i

) = g

k+1

,.. .,i

) (39)

3.5 Numerical Computation of

Derivatives

From sampled values f

−l

,.. ., f

−1

, f

,.. ., f

points −lh, .. .,−h, 0,h,. .. ,kh, n = k + l + 1, set

of equations from Taylor polynomials can be con-

structed.

∀i ∈ {−l, −l + 1,. .., −1,0, 1,.. .,k − 1,k} :

= f

∑

m=1

(m)

(0) (40)

Written in matrix form:

b =







−l

− f

−l+1

− f

...

−1

− f

...

k−1

− f







A =







(−l)

... (−l)

(−l + 1)

... (−l + 1)

...

(−1)

... (−1)

(1)

... (1)

...

(k − 1)

... (k − 1)

(k)

... (k)







x =





(1)

(0)

...

(n)

(0)





x = A

−1

b (41)

Vector x represents a vector of Taylor terms.

Terms in x can be transformed (transformation de-

noted by G) into derivatives.

For given numbers (l,k), matrix b changes, A

−1

stays the same. From now on, this system is

going to be denoted as κ

l,k

and its solution as

l,k

( f

−l

,.. ., f

) = G(A

−1

b).

3.6 Approximation of I

The main task is to solve the following integral.

= I

) =

, p

)dx

(42)

It can be transformed into an initial value problem.

(t) = g

(t, p

) I

(0) = 0 (43)

Solved by Taylor polynomial the system can be

written as follows

) = I

(0) +

α(p

,1)

∑

m=1

(m)

(0)

(2h

) = I

) +

α(p

,2)

∑

m=1

(m)

) (44)

) = I

) +

α(p

)

∑

m=1

(m)

)

where d

= d

− 1. Substituting (43) into (44):

) = I

(0) +

α(p

,1)

∑

m=1

(m−1)

(0, p

) (45)

(2h

) = I

) +

α(p

,2)

∑

m=1

(m−1)

, p

) (46)

) = I

) +

α(p

)

∑

m=1

(m−1)

, p

)

(47)

Derivatives of g

(t, p

) cannot be computed ana-

lytically, because g

is a sampled function. However,

the sampled values can be used to compute numerical

derivatives

(m)

(0, p

) = x

(m),1 ≤ m ≤ n (48)

NumericalIntegrationofMultipleIntegralsusingTaylorPolynomial

167

where

= κ

0,n

(0, p

),g

, p

),.. .,g

(nh

, p

)) (49)

Generally for x

= κ

l,m

(i + j

, p

),.. .,g

(i + j

|β(i,k)|

, p

))

β(i,k) = {−l, ... ,m}, j

,.. ., j

|β(i,k)|

∈ β(i,k),

< j

< ··· < j

|β(i,k)|

,i + j

≥ 0

where β(i,k) stands for a set of indeces in time ih

for p

, x

’s ﬁrst coordinate has index 1.

(m)

(ih

, p

) = x

(m),1 ≤ m ≤ n (50)

) = E

α(p

,1)

∑

m=2

(m − 1) (51)

(2h

) = E

α(p

,2)

∑

m=2

(m − 1) (52)

...

) = E

α(p

)

∑

m=2

(m − 1) (53)

where E

= I

(0) + g

( jh

, p

), d

= d

− 1.

From (35)

= κ

l,m

(i+ j

)

(i+ j

)

,.. .,I

(i+|β(i,k)|,p

)

) (54)

4 INTEGRATION OF AN

EXPONENTIAL FUNCTION

The method was tested on a computation of double in-

tegral of an exponential function, i.e.

x+y

dydx.

Tests were run for a different lengths of an integra-

tion step, number of Taylor terms and arithmetic pre-

cision. Precision is determined by a number of bits

used for the mantissa of each number. Numerical so-

lution was compared with an analytical solution of the

double integral. Error of computation for each test in-

stance is shown in table 1. For ﬁxed integration step

and precision, only a number of the Taylor term with

the smallest error is shown.

5 COMPUTATION OF TAYLOR

TERMS

In order to compute a value of function f (h) at h, the

following equation is used.

f (h) = f (0) +

(1)

(0)

h +

(2)

(0)

+ .. . (55)

Table 1: Error of computation of

x+y

dydx.

step no. of terms precision [bits] error

0.2 11 400 1.13e-06

0.1 19 400 8.95e-20

0.05 39 400 6.88e-52

0.04 49 400 9.14e-70

0.02 99 800 8.02e-170

0.01 104 900 8.09e-208

0.005 94 900 4.59e-217

0.004 91 900 4.13e-220

0.002 85 900 3.49e-227

The equation can be expressed using Di terms.

f (h) = f (0) + D1 + D2 + D3 + . .. (56)

The terms can be computed using combined

method, where I

are samples from which terms (b

column vector) can be computed. Matrix A is a spe-

cial form of matrix and x is a vector of the correspond-

ing terms.

b =







− I

...

− I

...

− I







A =







1 1

... 1

2 2

... 2

...

j j

... j

...

n n

... n







x =







...

D j

...







In matrix equation form.

Ax = b (57)

The terms can be then computed by solving the

matrix.

x = A

−1

b (58)

In order to compute x, it is necessary to compute

inverse of matrix A.

5.1 Rate of Change of Taylor Terms

The number of terms n to be computed depends on the

precision, i.e. it is a function of ε, i.e. n(ε). The ideal

case is when the terms form a descending sequence.

| > |D

| > ... (59)

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

168

The function n(ε) is then given.

n(ε) = sup{i||D

| < ε} (60)

Generally, this is not the case. In order to ﬁnd

n(ε), it is necessary to ﬁnd a decreasing sequence U(i)

such that U(i) >= |Di|.

n(ε) = sup{i|U

< ε} (61)

Looking at equation (58) i-th term is given as a dot

product of i-th row of A

−1

and x.

= a

−1

x (62)

From (62) it can see the value of D

depends only

on the A

−1

(which is independent of h) and x (depen-

dent of h). In order to construct n(ε), inverse matrix

and x have to be analyzed.

5.2 Analysis of A

−1

and x

Dot product (62) can be over-approximated. Vector

x is given as a difference of samples I

. Taking the

maximum value M and the minimum value m value of

samples, new vector x

= (M − m,M − m,. .. ,M − m)

is constructed. Then x ≤ x

. For the product, if x ≥ 0

the following holds.

| = |a

−1

x| =



∑

j=1

−1

i, j



∑

−1

i, j

−1

i, j

∑

−1

i, j

−1

i, j



(63)

For sum of positive members.

∑

−1

i, j

−1

i, j

≤

∑

−1

i, j

−1

i, j

(M − m) =

(M − m)

∑

−1

i, j

−1

i, j

= (M − m)P(i) (64)

For sum of negative members.

∑

−1

i, j

−1

i, j

≥

∑

−1

i, j

−1

i, j

(M − m) =

(M − m)

∑

−1

i, j

−1

i, j

= (M − m)N(i) (65)

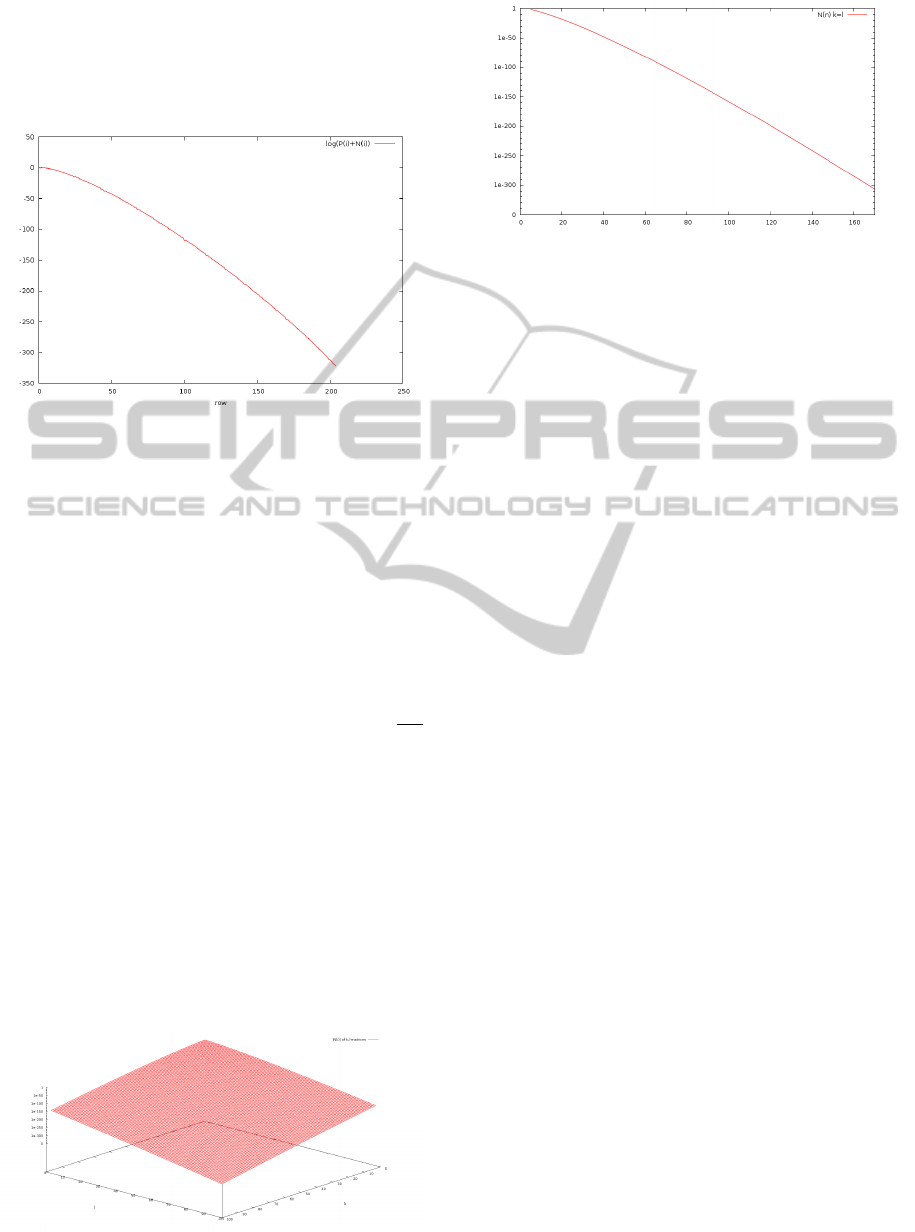
Figure 3 shows the progress of summing the posi-

tive and negative members of matrix with 93 samples

taken from the left and 113 samples taken from the

right of a sampled function f . The sum of all mem-

bers can be seen in Figure 4. Multiplying positive

members with M − n implies greater sum. Thus the

entire sum is the upper bound of the term. Multi-

plying negative members with M − m implies smaller

sum. Now the question is how big is the decrease.

Expressing M − n in powers of 10.

M − n = 10

(66)

If all components of x on index of negative mem-

bers of row i are smaller than 1, their weighted sum

N(i) increases. Thus an upper bound is still obtained.

If there is a component c

> 1, the sum is decreased.

If c

is substited with M − m, the sum is decreased by

(M − m − c

i, j

. In general, the decrease is given as

∑

(M − m − c

i, j

, because M − n > M − n − c

(as M − n > c

∆ =

∑

(M − m − c

)|a

−1

i, j

| ≤

∑

(M − m)|a

−1

i, j

| =

= (M − m)

∑

−1

i, j

| (67)

This decrease for i-th row will be denoted as ∆(i).

Figure 3: Sum of positive members as a function of row

number.

To compensate for the decrease ∆(i), let’s ﬁrst take

a look at Figure 3 again. Adding −∆(i) to N(i), N(i)

is decreased by a factor of 10

. Assuming N(i) and

P(i) are of the same order, the resulting sum is de-

creased by the same factor of 10

. Denoting

∑

j=1

−1

i, j

as S(i) and putting it all together.

|Di| ≤ |(M − n)P(i) + (M − n)N(i) + ∆(i)| =

= |(M − m)S(i) + ∆(i)| (68)

Because ∆(i) ≤ (M − m)|N(i)|.

|Di| ≤ |(M − m)S(i) + ∆(i)| ≤

(M − m)|S(i)| + ∆(i) ≤

(M − m)|S(i)| + (M − m)|N(i)| = (69)

(M − m)(|S(i)| + |N(i)|)

NumericalIntegrationofMultipleIntegralsusingTaylorPolynomial

169

Assuming |N(i)| ≥ |S(i)| terms are upper bounded

only by N(i).

|Di| ≤ (M − m)(|N(i)| + |N(i)|) =

= 2(M − m)|N(i)| ≈ 10

|N(i)| (70)

Figure 4: Sum of negative members as a function of row

number.

Inequality (70) is valid because given values N(i)

and P(i) are very similar and their sum S(i) has

smaller exponent. However any weighted sum with

weights different from w

= 1 changes mantissa of

both N(i) and P(i) and their sum D(i) therefore has

bigger exponent.

Thus using (M −m)S(i) for upper bound results in

smaller value, but with a suitable vector x, weighted

sum of Di can give greater value than (M − m)S(i).

From observation, S(i) is always smaller than N(i).

The higher the dimension of A, the greater ratio

N(i)

S(i)

(in positive powers of 10). For example, for dimen-

sion equal to 400, the ratio can be 10

Figure 5 shows N(n) of the last row for each k,l-

matrix on h3; 100i × h3;100i (k stands for a number

of samples taken from left, l for a number of samples

taken from the right). Symmetry in sums of negative

members can be seen. For k = l the greatest sum is

obtained. If k 6= l, the sum gets smaller. To eliminate

dependency on k and l, only cases, where k = l need

to be analyzed.

Figure 6 shows the case where k + l = n. It can be

seen, that the graph decreases as n increases.

Figure 5: |N(n)| of A

−1

as a function of n.

Figure 6: |N(n)| for k = l as a function of n.

6 COMPUTATION OF N(I)

The number of terms needed to compute the Taylor

series depends on the quality of the approximation of

the decreasing upper bound of an absolute value of

the sum of the last row for each dimension.

6.1 Approximation of a N(i) of the Last

Rows

The better approximation of the upper bound the

smaller number of Taylor terms needed. Denoting the

upper bound as s(n) minimization problem is to min-

imize error

err =

∞

∑

i=1

||Di| − s(i)| (71)

given the following equations:

|Di| ≤ s(i)∀i ∈ N (72)

s(i) > s(i + 1)∀i ∈ N (73)

6.2 State of the Art Approximation

Figure 7 shows an approximation of log(|N(n)|) by a

function:

g(n) = −nlog

(n) + b (74)

where a = 21.1 and b = 40.

In the Figure 7 function g(n) is an upper bound

of the graph. Values a and b were determined experi-

mentally.

Function g(n) is given by multiplication of loga-

rithmic and linear function. As logarithm is negative

and determines a tangent, g(n) is decreasing function

of n.

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

170

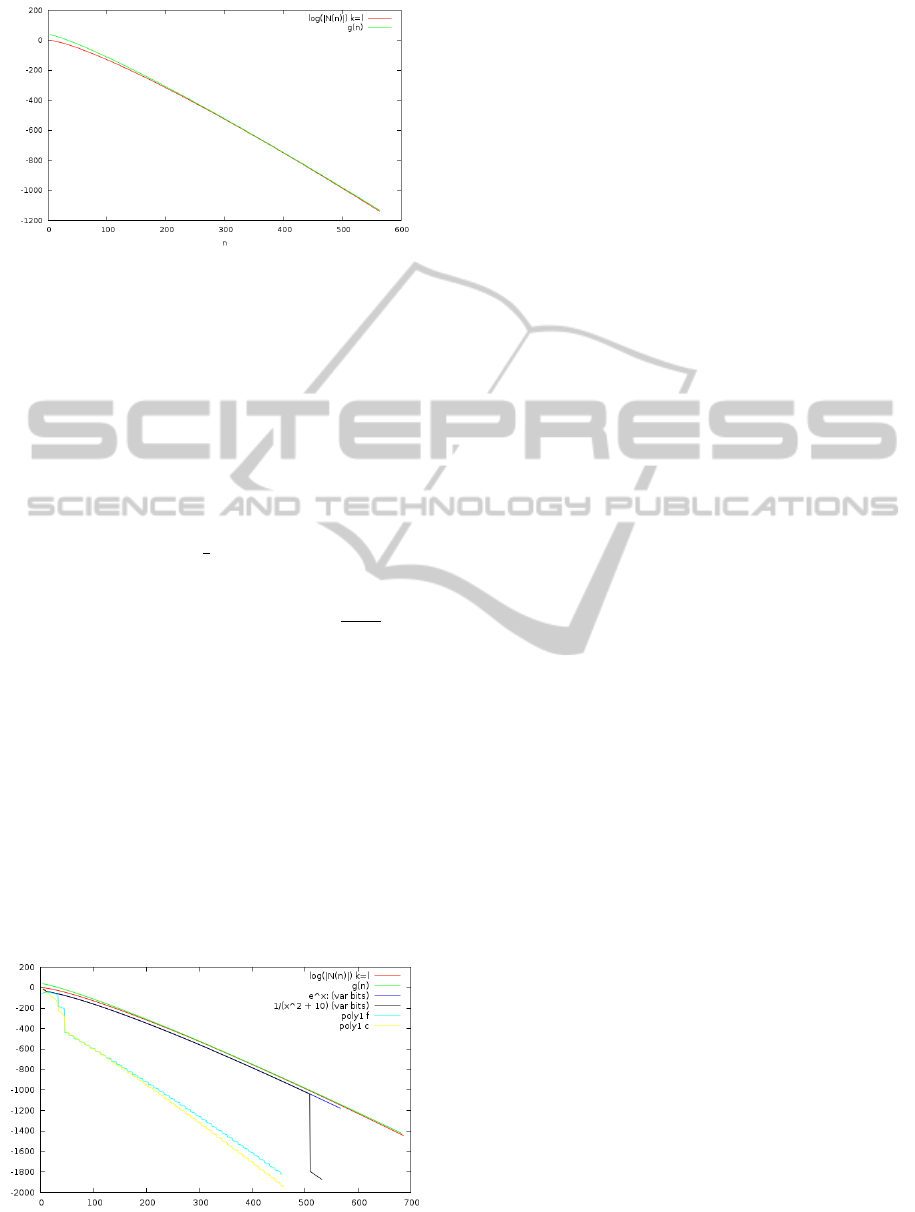
Figure 7: Approximation of g(n).

Upper bound s(n) is given by the following equa-

tion.

s(n) = (M − m)10

40−nlog

21.1

(n)

(75)

= 10

e+40−nlog

21.1

(n)

7 TEST OF THE UPPER BOUND

Figure 8 shows progress of computed value of Di of

a function e

for k = l =

. Graph e

gives a value of

’s D(n). As we can see its values are upper bounded

by s(n). Bound log(|N(i)|) still holds for this case as

M − m is of order 10

. Second function is

+10

. It is

upper bounded again, M − m is of order 10

−2

. Poly-

nomial function 10

+ 10

test a case where

a range of ﬁrst to 32-th terms are equal to 0, 33-th

derivative is non-zero, 34-th to 44-th equal to 0, 45-

th non-zero and the higher are equal to 0. Forward

method poly1 f (Figure 8) is used for this case as it

computes derivatives in time 0. The polynom is for

the ﬁrst 100 samples of order 10

−9

. As it can be seen

in the graph it is still upper bounded. However the

bound is too high and multiplicator (M − m) must be

analyzed to give better upper bound. The same apply

for poly1 c (Figure 8). It uses combined method with

samples of order 10

Figure 8: Approximation of Di by g(n).

8 CONCLUSIONS

New method for numerical integration of a function of

n-variables has been introduced. It is based on Taylor

polynomials and computation of its terms from dif-

ferential equations previously solved. Determining an

optimal number of terms for each polynomial is still

an open problem. Further analysis of a dot product is

required.

The method has been tested on integrals with

known analytical solution. Only hyper-cubical inte-

gration areas were explored so far.

ACKNOWLEDGEMENTS

This paper has been elaborated in the framework of

the project New creative teams in priorities of scien-

tiﬁc research, reg. no. CZ.1.07/2.3.00/30.0055 (as

well as the the IT4Innovations Centre of Excellence

CZ.1.05/1.1.00/ 02.0070), supported by Operational

Programme Education for Competitiveness and co-

ﬁnanced by the European Social Fund and the state

budget of the Czech Republic. The paper includes the

solution results of the international AKTION research

project Number 69p22 and the internal BUT projects

FIT-S-12-1 and FIT-S-14-2486.

REFERENCES

F. Khaksar Haghani, F. Soleymani. (2014). A New High-

Order Stable Numerical Method for Matrix Inversion.

The Scientiﬁc World Journal, Volume 2014

A. Jordan, Z. Maorong. (2005). A Software Package for

the Numerical Integration of ODEs by Means of High-

Order Taylor Methods. Experimental Mathematics,

Vol. 14, No. 1

A. Abad, R. Barrio, F. Blesa, M. Rodriguez. (2012). Al-

gorithm 924: TIDES, a Taylor Series Integrator for

Differential EquationS. ACM Transactions on Mathe-

matical Software, Vol. 39, No. 1, Article 5.

NumericalIntegrationofMultipleIntegralsusingTaylorPolynomial

171