
Diagonal Stability of Uncertain Interval Systems
Vakif Dzhafarov (Cafer)
1
, Taner B¨uy¨ukk¨oro˘glu
1
and Bengi Yıldız
2
1
Department of Mathematics, Faculty of Science, Anadolu University, 26470 Eskisehir, Turkey
2
Department of Mathematics, Faculty of Science and Letters, Bilecik Seyh Edebali University,
Gulumbe Campus, 11210 Bilecik, Turkey
Keywords:
Hurwitz Diagonal Stability, Schur Diagonal Stability, Common Diagonal Solution, Interval Matrices, Game
Problem.
Abstract:
In this paper we consider the problem of diagonal stability of interval systems. We investigate the existence
and evaluation of a common diagonal solution to the Lyapunov and Stein matrix inequalities for third order
interval systems. We show that these problems are equivalent to minimax problem with polynomial goal
functions. We suggest an interesting approach to solve the corresponding game problems. This approach
uses the opennes property of the set of solutions. Examples show that the proposed method is effective and
sufficiently fast.
1 INTRODUCTION
Consider state equation
˙x = Ax
where x = x(t) ∈ R
n
and A = (a
ij
) (i, j = 1, 2, . . . , n)
is n×n matrix. In many control system applications
each entry a
ij
can vary independently within some in-
terval. Such systems are called interval systems. In
other words a
ij
≤ a
ij
≤ a
ij
where a
ij
, a
ij
are given.
Denote the obtained interval family by A, i.e.
A = {A = (a
ij
) : a
ij
≤ a
ij
≤ a
ij
, (i, j = 1, 2, . . . , n)}.
(1)
Interval matrices have many engineering applications.
Due to its natural tie with robust control system analy-
sis and design, several approach have involved for the
stability analysis of interval matrices (see (Barmish,
1994; Rohn, 1994; Bhattacharyya et al., 1995; Liber-
zon and Tempo, 2004; Pastravanu and Matcovschi,
2015; Yıldız et al., 2014)).
We are looking for the existence and evaluation of
a common diagonal Lyapunov function which guar-
antees diagonal stability of interval systems. In other
words we investigate the problem of existence of a di-
agonal matrix D = diag(x
1
, x
2
, . . . , x
n
) with x
i
> 0 and
with the property
A
T
D+ DA < 0 for all A ∈ A (2)
where the symbol “T” stands for the transpose and
“<” means negative definiteness.
Diagonal stability have many applications and this
problem has been considered in many works (see (Ar-
cat and Sontag, 2006; Johnson, 1974; Ziolko, 1990;
Kaszkurewicz and Bhaya, 2000; Khalil, 1982; Pas-
travanu and Matcovschi, 2015; Oleng and Narendra,
2003; B¨uy¨ukk¨oro˘glu, 2012; Yıldız et al., 2014) and
references therein).
An algebraic characterization of necessary and
sufficient conditions for the existence of a diagonal
Lyapunov function for a single third order matrix has
been derived in (Oleng and Narendra, 2003). The
algorithm submitted in (Pastravanu and Matcovschi,
2015) for a common diagonal solution of interval ma-
trix family is not effective since it uses complicated
bilinear matrix inequalities and the solver PENBMI.
2 COMMON DIAGONAL
SOLUTION FOR 3×3
INTERVAL SYSTEMS
In this section for 3×3 interval family we give nec-
essary and sufficient condition for the existence of
Hurwitz common diagonal solution and the corre-
sponding solution algorithm.
Consider 3×3 interval family
558
Dzhafarov (Cafer) V., Büyükköro
˘
glu T. and Yildiz B..
Diagonal Stability of Uncertain Interval Systems.
DOI: 10.5220/0005540605580562
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 558-562
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

A =
A =
a
1
a
2
a
3
a
4
a
5
a
6
a
7
a
8
a
9
:
a
i
∈ [a
−
i
, a
+
i
], (i = 1, 2, . . . , 9)
. (3)
Without loss of generality all 3 ×3 positive diag-
onal matrices diag(x
1
, x
2
, x
3
) with x
i
> 0 (i = 1, 2, 3)
may be normalized to have the form
D = diag(t, 1, s) =
t 0 0
0 1 0
0 0 s
with t > 0, s > 0.
Problem 1. Is there D = diag(t, 1, s) with t > 0, s > 0
such that
A
T
D+ DA < 0 (4)
for all a
i
∈[a
−
i
, a
+
i
] (i = 1, 2, . . . , 9).
We write
A
T
D+ DA =
2ta
1
ta
2
+ a
4
ta
3
+ sa
7
ta
2
+ a
4
2a
5
sa
8
+ a
6
ta
3
+ sa
7
sa
8
+ a
6
2sa
9
The matrix inequality (4), i.e. the negative definite-
ness of A
T
D+ DA is equivalent to the following
i) a
1
< 0
ii) (a
2
t + a
4
)
2
−4a
1
a
5
t < 0
iii) d
0
(t, a
1
, . . . , a
9
) + d
1
(t, a
1
, . . . , a
9
)s +
d
2
(t, a
1
, . . . , a
9
)s
2
< 0.
The functions d
i
(i = 1, 2, 3) are low order polynomi-
als and can be explicitly evaluated.
i) is satisfied for all a
1
∈ [a
−
1
, a
+
1
] if and only
if a
+
1
< 0. The problem of existence of a com-
mon t satisfying ii) for all (a
1
, a
2
, a
4
, a
5
) is equivalent
to the existence of a common diagonal solution for
2×2 family
a
1
a
2
a
4
a
5
and has been investigated in
(Yıldız et al., 2014). There whole interval of com-
mon t (in the case of nonempty) has been calculated.
If this interval is empty then there is no common
D = diag(t, 1, s) satisfying (4). Assume that this in-
terval (α, β) of common t is nonempty. Then the
existence of a common D = diag(t, 1, s) means that
there exist t ∈ (α, β) and s > 0 such that iii) is satis-
fied for all (a
1
, a
2
, . . . , a
9
). This problem is a game
problem. Indeed denote the left-hand side of iii) by
f(t, s, a
1
, . . . , a
9
). Then iii) is equivalent to the fol-
lowing minimax inequality
inf
t∈(α,β), s>0
max
(a
1
,...,a
9
)
f(t, s, a
1
, . . . , a
9
) < 0. (5)
Solve the game problem (5) is difficult in general, this
game has no a saddle point due to nonconvexityof the
function f.
We suggest the following interesting approach to
solve (5) numerically. This approach is based on the
openness property of the solution set of (4) . In other
words the following proposition is true.
Proposition 2.1. If there exist a common D =
diag(t
∗
, 1, s
∗
) then there exist intervals [t
1
,t
2
] and
[s
1
, s
2
] which contain t
∗
and s
∗
respectively such that
the matrix D = diag(t, 1, s) is a common solution for
all t ∈ [t
1
,t
2
], s ∈ [s
1
, s
2
].
Due to this proposition we suggest the following
algorithm for a common diagonal solution.
Algorithm 1. Let the interval family (3) be given.
i) Using the results on 2 ×2 interval systems from
(Yıldız et al., 2014) calculate the interval (α, β) for
t.
ii) Determine an upper bound
s for the variable s
from the positive definiteness condition of a suit-
able submatrix of −(A
T
D+ DA).
iii) Divide the interval [α, β] into k equal parts
[α
i
, β
i
] and the interval [0,
s] into m equal parts
[s
−
j
, s
+
j
].
iv) On each box
[α
i
, β
i
] ×[s
−
j
, s
+
j
] ×[a
−
1
, a
+
1
] ×···×[a
−
9
, a
+
9
]
consider the maximization of the polynomial func-
tion f(t, s, a
1
, . . . , a
9
).
If there exist indices i
∗
and j
∗
such that the max-
imum is negative then stop. The whole interval
[α
i
∗
, β
i
∗
] ×[s
−
j
∗
, s
+
j
∗
] defines family of common diag-
onal solutions.
As can be seen the above game problem (5) is re-
duced to a finite number of maximization problems in
which low order multivariable polynomials are maxi-
mized over boxes. These optimizations can be carried
out by Maple program or by the Bernstein expansion.
The following examples shows that Algorithm 1 is
sufficiently effective.
Example 2.1. Consider the interval family
−4 q
1
1
1 −4 q
2
q
3
1 −5
where q
1
∈[2, 3], q
2
∈[1, 2] and q
3
∈[1, 2]. We obtain
A
T
D+ DA =
−8t q
1
t + 1 t + q
3
s
q
1
t + 1 −8 s+ q
2
t + q
3
s s+ q
2
−10s
.
The 2×2 leading principal minor gives
64t −(q
1
t + 1)
2
> 0 ⇒ 64t > (q
1
t + 1)
2
,
max
q
1
∈[2,3]
(q
1
t + 1)
2
= (3t + 1)
2
< 64t,
DiagonalStabilityofUncertainIntervalSystems
559
9t
2
−58t+ 1 < 0, t ∈ (0.0173, 6.427).
Hence 64t −(q
1
t + 1)
2
> 0 for all t ∈(0.0173, 6.427),
q
1
∈ [2, 3].
The positive definiteness of the submatrix
8 −(s+ q
2
)
−(s+ q
2
) 10s
gives 80s −(s + q
2
)
2
> 0 or max
q
2
(s + q
2
)
2
< 80s or
(s+2)
2
< 80s or s
2
−76s+4< 0 and the upper bound
s = 80 is suitable.
We divide the intervals [0.0173, 6.427] and [0, 80]
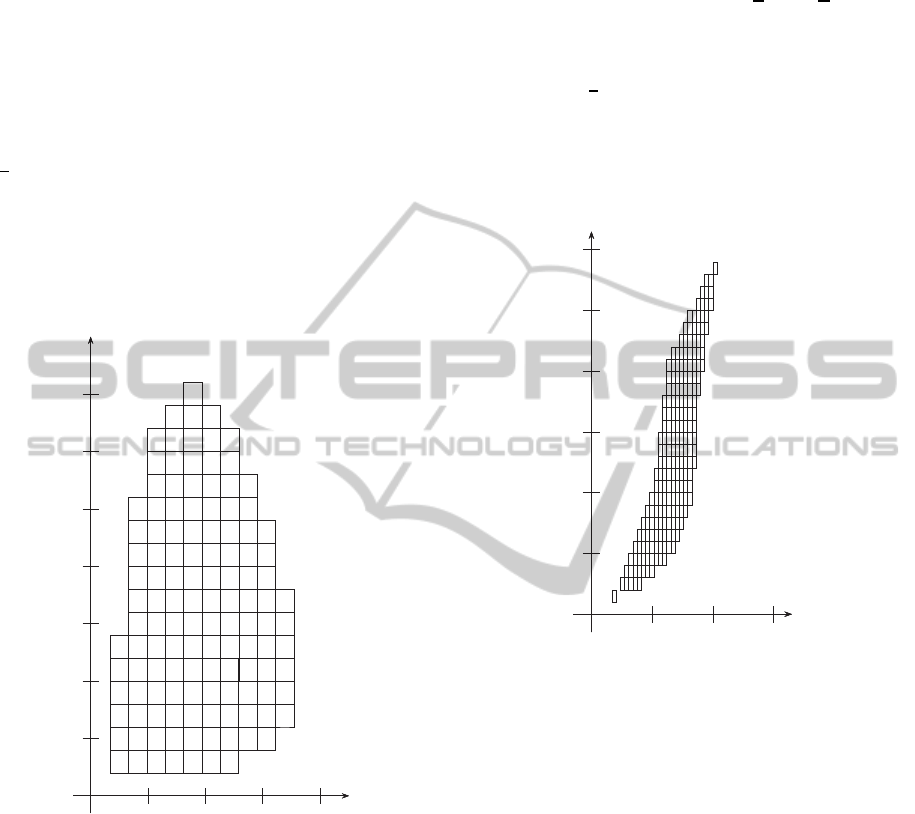
into 20 and 200 equal parts respectively. In Figure 1,
it is shown the family of boxes on which the deter-
minant det(A
T
D+ DA) is negative for all q
1
∈ [2, 3],
q
2
∈ [1, 2] and q
3
∈ [1, 2].
1
2
3
4
5
6
7
1 2 3 4
t
s
Figure 1: Each (t, s) from each box gives common diagonal
solution D = diag(t, 1, s).
Example 2.2. Consider the interval family
−3 q
1
−5
q
2
−2 1
q
3
q
4
−6
where q
1
∈ [1, 2], q
2
∈ [1, 2], q
3
∈ [4, 6] and q
4
∈
[−3, −1]. We obtain
A
T
D+ DA =
−6t q
1
t + q
2
−5t + q
3
s
q
1
t + q
2
−4 q
4
s+ 1
−5t + q
3
s q
4
s+ 1 −12s
.
Again
24t −(q
1
t + q
2
)
2
> 0 ⇒24t > (q
1
t + q
2
)
2
,
max
q
1
∈[1,2], q
2
∈[1,2]
(q
1
t + q
2
)
2
= (2t + 2)
2
< 24t,
t
2
+ 2t + 1 < 0, t ∈ (2−
√
3, 2+
√
3).
Hence 24t−(q
1
t + q
2
)
2
> 0 for allt ∈ (0.268, 3.732),
q
1
∈ [1, 2] and q
2
∈ [1, 2].
The value
s = 50 is acceptable. We divide the
intervals [0.268, 3.732] and [0, 50] into 50 and 200
equal parts respectively. Figure 2 gives all boxes on
which det(A
T
D + DA) is negative for all q
1
∈ [1, 2],
q
2
∈ [1, 2], q
3
∈ [4, 6] and q
4
∈ [−3, −1].
1
2
3
4
5
6
1 2 3
t
s
Figure 2: Each (t, s) from each box gives common diagonal
solution D = diag(t, 1, s).
It should be noted that the sufficient condition
from (Pastravanu and Matcovschi, 2015, Theorem 1)
is not satisfied for this example since for the matrix
U from Theorem 1 the maximum real eigenvalue is
positive.
3 DISCRETE SYSTEMS (SCHUR
STABILITY)
Common diagonal stability of discrete interval sys-
tems is equivalent to the existence of a positive di-
agonal matrix D which satisfies the following matrix
inequality
A
T
DA−D < 0 for all A ∈A (6)
where A is given by (1).
The case n = 2 has been solved in (Yıldız et al.,
2014). In the case of n = 3 taking again D =
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
560

diag(t, 1, s) we get
A
T
DA−D =
ta
2
1
+ a
2
4
+ sa
2
7
−t ta
1
a
2
+ a
4
a
5
+ sa
7
a
8
ta
1
a
2
+ a
4
a
5
+ sa
7
a
8
ta
2
2
+ a
2
5
+ sa
2
8
−1
ta
1
a
3
+ a
4
a
6
+ sa
7
a
9
ta
2
a
3
+ a
5
a
6
+ sa
8
a
9
ta
1
a
3
+ a
4
a
6
+ sa
7
a
9
ta
2
a
3
+ a
5
a
6
+ sa
8
a
9
ta
2
3
+ a
2
6
+ sa
2
9
−s
From the principal minors condition the negative def-
initeness of the above matrix is equivalent to three
polynomial inequalities.
Denote
f
1
(t, s, a
1
, a
4
, a
7
) = t(a
2
1
−1) + sa
2
7
+ a
2
4
,
f
2
(t, s, a
1
, . . . , a
8
) = Minus 2×2
leading principal minor,
f
3
(t, s, a
1
, . . . , a
9
) = Determinant.
Then the problem (6) is equivalent to the following:
Is there a positive pair (t, s) such that
f
1
< 0, f
2
< 0, f
3
< 0 (7)
for all (a
1
, a
2
, . . . , a
9
).
Now we can suggest the following algorithm.
Algorithm 2. Let 3×3 interval family (3) be given.
i) Using the results on 2 ×2 interval systems from
(Yıldız et al., 2014) calculate the interval (α, β) for
the variable t.
ii) Determine an upper bound
s for s.
iii) Divide the interval [α, β] into k equal parts
[α
i
, β
i
] and the interval [0,
s] into m equal parts
[s
−
j
, s
+
j
].
iv) On each box
[α
i
, β
i
] ×[s
−
j
, s
+
j
] ×[a
−
1
, a
+
1
] ×···×[a
−
9
, a
+
9
]
consider the maximization of the polynomial func-
tions f
i
(i = 1, 2, 3).
If there exist indices i
∗
and j
∗
such that the max-
imum each of three functions f
k
(k = 1, 2, 3) is
negative then stop. The whole interval [α
i
∗
, β
i
∗
] ×
[s
−
j
∗
, s
+
j
∗
] defines family of common diagonal solu-
tions.
Example 3.1. Consider the interval family
−0.5 0.3 q
1
q
2
−0.3 −0.6
−0.2 q
3
0.1
where q
1
∈ [−0.2, 0.4], q
2
∈ [−1, 0] and q
3
∈ [0, 0.2].
We obtain
A
T
DA−D =
−0.75t + q
2
2
+ 0.04s −0.15t−0.3q
2
−0.2q
3
s
−0.15t −0.3q
2
−0.2q
3
s 0.09t + q
2
3
s−0.91
−0.5q
1
t −0.6q
2
−0.02s 0.3q
1
t + 0.1q
3
s+ 0.18
−0.5q
1
t −0.6q
2
−0.02s
0.3q
1
t + 0.1q
3
s+ 0.18
q
2
1
t −0.99s+ 0.36
.
We get [α, β] = [1.3494, 7.5833] and
s = 20. Divide
the intervals [1.3494, 7.5833] and [0, 20] into 20 and
50 equal parts respectively. In Figure 3, it is shown
the family of boxes on which all three functions f
k
(k = 1, 2, 3) are negative for all q
1
∈ [−0.2, 0.4], q
2
∈
[−1, 0] and q
3
∈ [0, 0.2].
1
2
3
4
5
6
7
8
9
1 2 3 4
t
s
Figure 3: Each (t, s) from each box gives common diagonal
solution D = diag(t, 1, s).
4 CONCLUSIONS
In this paper we consider the problem of diagonal sta-
bility of interval systems. The proposed approach is
based on finding common diagonal Lyapunov func-
tions. Both Hurwitz (continuouscase) and Schur (dis-
crete case) stability are considered for third order sys-
tems. We suggest an interesting approach to solve the
corresponding game problems.
DiagonalStabilityofUncertainIntervalSystems
561

REFERENCES
Arcat, M. and Sontag, E. (2006). Diagonal stability of a
class of cyclic systems and its connection with the se-
cant criterion. Automatica, 42(9):1531-1537.
Barmish, B. R. (1994). New Tools for Robustness of Linear
Systems. Macmillan, New York.
Bhattacharyya, S. P., Chapellat, H., and Keel, L. H. (1995).
Robust Control: The Parametric Approach. Prentice
Hall, Upper Saddle River.
B¨uy¨ukk¨oro˘glu, T. (2012). Common diagonal lyapunov
function for third order linear switched system. Jour-
nal of Computational and Applied Mathematics,
236:3647-3653.
Johnson, C. R. (1974). Sufficient condition for d-stability.
J. Econom., 9(1):53-62.
Kaszkurewicz, E. and Bhaya, A. (2000). Matrix diago-
nal stability in systems and computation. Birkhuser,
Boston.
Khalil, H. K. (1982). On the existence of positive diago-
nal p such that PA+ A
T
P < 0. IEEE Trans. Automat.
Control, AC-27(1):181-184.
Liberzon, D. and Tempo, R. (2004). Common lyapunov
functions and gradient algorithms. IEEE Trans. Au-
tomat. Control, 49(6):990-994.
Oleng, N. O. and Narendra, K. S. (2003). On the exis-
tence of diagonal solutions to the lyapunov equation
for a third order system. In Proceedings of the Ameri-
can Control Conference, volume 3, pages 2761-2766.
IEEE.
Pastravanu, O. and Matcovschi, M. (2015). Sufficient con-
ditions for schur and hurwitz diagonal stability of
complex interval matrices. Linear Algebra and its Ap-
plications, 467:149-173.
Rohn, J. (1994). Positive definiteness and stability of inter-
val matrices. SIAM J. Matrix Anal., 15(1):175-184.
Yıldız, B., B¨uy¨ukk¨oro˘glu, T., and Dzhafarov, V. (2014).
Common diagonal stability of second order inter-
val systems. In the 11th International Conference
on Informatics in Control, Automation and Robotics
(ICINCO-2014), pages 223-227. SCITEPRESS.
Ziolko, M. (1990). Application of Lyapunov functionals to
studying stability of linear hyperbolic systems. IEEE
Trans. Automat., 35(10):1173-1176.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
562
