Practical IBE Secure under CBDH - Encrypting Without Pairing
S. Sree Vivek
1
, S. Sharmila Deva Selvi
2
, Aanchal Malhotra
3
and C. Pandu Rangan
4
1
Samsung R&D Institute, Bangalore, India
2
Microsoft Research India, Bangalore, India
3
Boston University, Boston, MA, U.S.A.
4
IIT-Madras, Chennai, India
Keywords:
Identity based Cryptography, Encryption without Bilinear Pairing, Without Full Domain Hash, Provable
Security, Random Oracle Model.
Abstract:
Since the discovery of identity based cryptography, a number of identity based encryption schemes were re-
ported in the literature. Although a few schemes were proposed after its introduction, the first efficient identity
based encryption scheme was proposed by Dan Boneh and Matthew K. Franklin in 2001. This encryption
scheme uses Weil pairing on elliptic curves during both encryption and decryption process. In this paper, we
propose a new identity based encryption scheme and prove its security in the random oracle model. There
are two highlighting features in our scheme. First, it does not employ bilinear pairing computation during
the encryption process. Second, our scheme does not require full domain hashing, which makes our scheme
more practical and efficiently implementable. Moreover, we prove the security of our scheme by reducing it
to the well known Computational Bilinear Diffie-Hellman problem. We first prove the security of our scheme
in weaker security notion i.e. we prove our scheme to be IND-CPA secure. Then using Fujisaki Okamoto
transformation, we convert our scheme to IND-CCA secure version.
1 INTRODUCTION
Identity-based (from now on, ID-based) cryptography
was introduced by Adi Shamir (Shamir, 1984) in his
seminal paper as an alternative to traditional public
key cryptography. Traditional public key cryptogra-
phy makes use of Public Key Infrastructures (PKI). In
PKI-based system, each user generates on his own his
private and public key. The certification authority of
the PKI provides a digital certificate which links the
identity of the user and his public key. The validity of
this certificate must be checked before using the pub-
lic key of the user, when encrypting a message to him
or when verifying a signature from him. Obviously,
the management of digital certificates degrades the ef-
ficiency of public key cryptosystems in practice. The
idea of ID-based cryptography is to use the identity of
a user (e-mail address, telephone number, etc.) as the
public key. The user contacts a trusted entity, Private
Key Generator (PKG), to obtain the private key cor-
responding to his identity. The PKG typically uses a
secret information called master secret to compute the
private key corresponding to the identity of the user.
This private key is then distributed to the authorised
user through a secure channel.
ID-based cryptography has been the object of a lot
of research during the last decade. ID-based encryp-
tion is an interesting technology because other public-
key algorithms have encountered difficulty in practi-
cal use. It provides an easy solution that provides for
the confidentiality of data. A number of ID-based en-
cryption schemes have been proposed in both stan-
dard model (Boneh and Boyen, 2011)(Agrawal et al.,
2010)(Kiltz, 2006)(Gentry, 2006)(Waters, 2005) and
random oracle model (Boneh and Franklin, 2005)(At-
trapadung et al., 2007)(Sakai and Kasahara, 2003).
The most efficient ID-based encryption schemes are
currently based on bilinear pairings on elliptic curves,
such as the Weil or Tate pairings. The first of these
schemes was developed by Dan Boneh and Matthew
K. Franklin (Boneh and Franklin, 2005) and performs
probabilistic encryption of arbitrary ciphertexts using
an Elgamal-like approach. Many ID-based encryp-
tion schemes have been proposed since then, adopting
many different strategies, thereby reducing the com-
putational cost and the ciphertext size.
Table 1 recollects the complete bibliography of
different ID-based Key constructs used till date.
251
Sree Vivek S., Sharmila Deva Selvi S., Malhotra A. and Pandu Rangan C..
Practical IBE Secure under CBDH - Encrypting Without Pairing.
DOI: 10.5220/0005541802510258
In Proceedings of the 12th International Conference on Security and Cryptography (SECRYPT-2015), pages 251-258
ISBN: 978-989-758-117-5
Copyright
c
 2015 SCITEPRESS (Science and Technology Publications, Lda.)

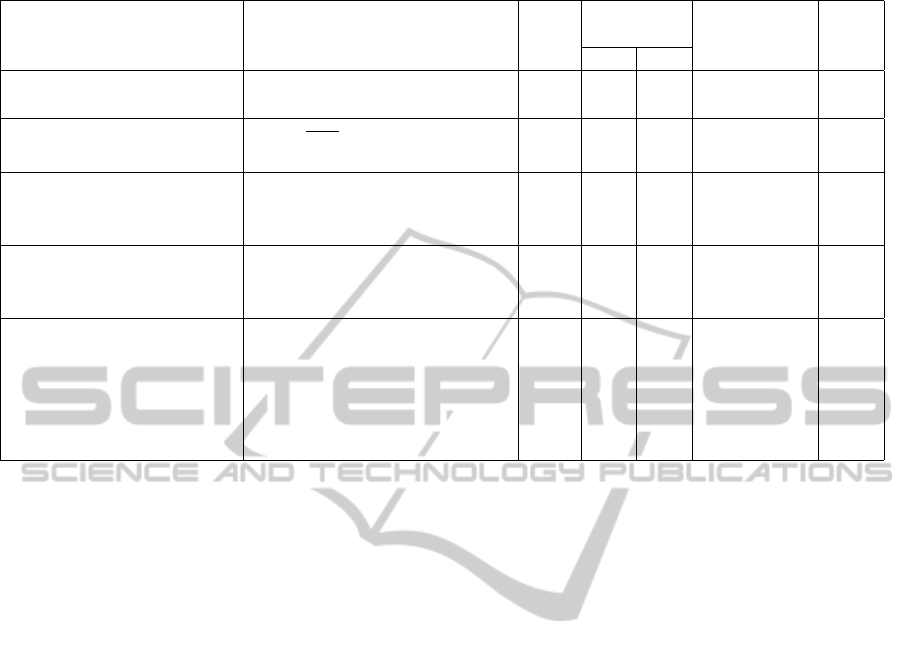
Table 1: Properties of existing ID-based Key constructs.
Scheme ID-based Key Constructs IBE Pairing Assumption FDH
Enc Dec
BLS D
A
= sQ
A
∈ G
1
Y Y Y CBDH Y
(Boneh et al., 2004) Q
A
=
ˆ
H(ID
A
) ∈ G
1
Barreto D
A
=
1
s+q
A
P ∈ G
1
Y N Y q-SBDH N
(Barreto et al., 2005) q
A
=
ˆ
H(ID
A
) ∈ Z
∗
q
Galindo d
A
= (x
A
+ s
1
q
A
) mod q ∈ Z
∗
q
N - - - -
(Galindo and Garcia, 2009) X
A
= x
A
P ∈ G
1
q
A
=
ˆ
H(ID
A
) ∈ Z
∗
q
Selvi d
A
= (s
1
q
A
+ s
2
x
A
) ∈ Z
∗
q
N - - - -
(Selvi et al., 2011) X
A
= x
A
P ∈ G
1
,Y
A
= y
A
P ∈ G
1
q
A
=
ˆ
H(ID
A
) ∈ Z
∗
q
Ours d
A
= (sq
A
+ r
A
) ∈ Z
p
Y N Y CBDH N
X
A
= r
A
Q+
¯r
A
(u
o
+
k
∑
i=1
q
A
[i]u
i
) ∈ G
1
Y
A
= ¯r
A
P ∈ G
1
q
A
=
ˆ
H(ID
A
) ∈ {0, 1}
k
Motivation. Typically, the computationally most ex-
pensive part of implementing ID-based encryption al-
gorithms is execution of bilinear pairings. Thus, our
main concern in this paper is to avoid bilinear pair-
ing during encryption. Till now, all but one scheme
by Sakai-Kasahara (Sakai and Kasahara, 2003) use
bilinear pairing during the encryption process. This
scheme is quite efficient, in terms of computational
complexity when compared with other ID-based en-
cryption schemes. Later, the security of this scheme
was proved by Chen and Cheng (Chen and Cheng,
2005) under q-SBDH assumption, which is a stronger
assumption. Our attempt was to construct a scheme
which reduces to a weaker and well known assump-
tion.
Secondly, in practice it is difficult to build a
Full Domain Hash (FDH) which hashes directly onto
a group of points on an elliptic curve (Boneh and
Franklin, 2005). However with a slightly reduced cost
in computation, it is achieved by hashing onto some
arbitrary set, and then using some deterministic ad-
missible encoding function to map onto the elliptic
curve group. In our scheme, instead of FDH we make
use of a computation similar to Waters’ hash (Waters,
2005) and hence our scheme can be easily and effi-
ciently realized in practice.
Our Contribution. Our first interesting contribution
is a novel probabilistic PKI based signature scheme
(and this is of specific interest) described in section 3.
The novelty of this signature scheme is; it is based on
Schnorr’s signature (Schnorr, 1989) but does not take
the randomness used to generate the signature as an
input to the message hash. In an ID-based scheme,
the private key of the user is constructed using a PKI
based signature scheme. While randomized signa-
ture schemes such as Schnorr (Schnorr, 1989),(Selvi
et al., 2011),(Galindo and Garcia, 2009),(Herranz,
2006) are used to extract the private key of the user in
ID-based signatures, they can not be used for extract-
ing the private key of a user for an ID-based encryp-
tion scheme. This is because the randomness used to
extract the private key should also be a component of
the public key of the ID-based scheme. While in an
ID-based signature scheme, this randomness can be
sent along with the signature for verification, it can
not be done in IBE scheme, since in an IBE scheme,
the public key of the user must be the identity alone.
Thus, in our IBE scheme we use a construction simi-
lar to Waters’ hash (Waters, 2005), which helps us to
achieve binding between the identity of the user and
the private key, without including the randomness in
the message hash. In addition, this helps us in avoid-
ing the use of full domain hashes in the design of the
ID-based encryption scheme. Next we show the con-
struction of the novel ID-based encryption scheme in
section 4 which does not use pairing during encryp-
tion process. However, during the decryption process
we require pairing computation. The significant ad-
vantage of our scheme is that it does not compromise
on security and is proven secure under the well known
CBDH assumption.
Table 2 compares different ID-based encryption
schemes in random oracle model in terms of underly-
SECRYPT2015-InternationalConferenceonSecurityandCryptography
252

Table 2: Properties of ID-based Encryption Schemes in Random Oracle Model.
Scheme Hard Problem Encryption Decryption Cipher Text
Assumption Complexity Complexity Size
Boneh Franklin CBDH 1P+2EM 1P ||G||+|m|
(Boneh and Franklin, 2005)
Katz and Wang GBDH 2P+4EM 1P 2||G||+2|m|
(Katz and Wang, 2003)
(Attrapadung et al., 2007)
Attrapadung et al LBDH 2P+2EM+1SKE 2P+2EM ||G||+|m| + 2ρ
(Attrapadung et al., 2007)
Sakai and Kasahara q-SBDH 3EM 1P+1EM ||G||+|m| + ρ
(Sakai and Kasahara, 2003)
Ours (Γ
0
scheme) CBDH ρEA+3EM 2P+1EM 2||G||+|m|+ρ
P - Pairing, EM - Elliptic curve scalar point multiplication, EA - Addition of two elliptic curve points, SKE - Complexity of CCA-2
secure Symmetric Key Encryption, ||G|| - Size of one group element, |m| - Size of message, ρ - Number typically of size 128 bits.
CBDH - Computational Bilinear Diffie-Hellman, GBDH - Gap Bilinear Diffie-Hellman, LBDH - List Bilinear Diffie-Hellman,
q-SBDH - q- Strong Bilinear Diffie-Hellman.
ing hard problem assumption, computation complex-
ity of encryption and decryption processes, and size of
generated ciphertext. Our scheme involves the com-
putation of elliptic curve point additions and avoids
the use of bilinear pairing during encryption. How-
ever, the time complexity for executing one bilinear
pairing is roughly four times the time complexity for
executing upto 160 elliptic curve point additions (Is-
lam and Biswas, 2012). From table 2, it is clear
that compared to other schemes, we have reduced
the computation cost during encryption process to a
great extent in our scheme by avoiding bilinear pair-
ing. There is one other scheme by Sakai and Kasa-
hara (Sakai and Kasahara, 2003) that does not involve
pairing computation during encryption. Although the
decryption cost of our scheme is higher than that of
(Sakai and Kasahara, 2003), we argue that our scheme
is better than the scheme in (Sakai and Kasahara,
2003). This is because the security of our scheme is
reduced to the well known CBDH problem whereas
the scheme in (Sakai and Kasahara, 2003) has a se-
curity reduction to the stronger q-SBDH assumption.
Similarly, the decryption cost of our scheme is higher
when compared with (Boneh and Franklin, 2005) but
our scheme offers two advantages over (Boneh and
Franklin, 2005). First our scheme does not involve
bilinear pairing computation during encryption, and
second it does not use Full Domain Hash, thus mak-
ing it efficiently implementable.
2 PRELIMINARIES
In this section, we briefly recall the basics and secu-
rity models.
2.1 Bilinear Pairing
Let G
1
be a cyclic additive group generated by P, with
prime order q, and G
2
be a cyclic multiplicative group
of the same order q. A bilinear pairing is a map ˆe :
G
1
× G
1
→ G
2
with the following properties.
Bilinearity. For all P, Q, R ∈ G
1
,
ˆe(P, Q + R) = ˆe(P, Q) ˆe(P, R).
ˆe(aP, bQ) = ˆe(P, Q)
ab
[W herea,b ∈
R
Z
p
].
Non-degeneracy. There exist P,Q ∈ G
1
such that
ˆe(P,Q) 6= I
G
2
, where I
G
2
is the identity element of
G
2
.
Computability. There exists an efficient algorithm to
compute ˆe(P,Q) for all P,Q ∈ G
1
.
2.2 Computational Assumptions
In this section, we review the computational assump-
tions related to bilinear maps that are relevant to the
protocol we discuss.
Let ˆe : G
1
× G
1
→ G
2
be a bilinear map. Let P be
a generator of G
1
, whose order is a large prime q. Let
a,b,c be elements of Z
p
.
Definition 1 (Computational Diffie-Hellman Prob-
lem (CDHP)). Given (P,aP,bP) ∈ G
3
1
for unknown a,
b ∈ Z
p
, the CDH problem in G
1
is to compute abP.
The advantage of any probabilistic polynomial time
algorithm A in solving the CDH problem in G
1
is de-
fined as:
Adv
CDH
A
= Pr[A(P, aP,bP) = abP|a,b ∈ Z
p
]
The CDH assumption is that, for any probabilistic
polynomial time algorithm A, the Adv
CDH
A
is negligi-
PracticalIBESecureunderCBDH-EncryptingWithoutPairing
253

bly small.
Definition 2 (Computational Bilinear Diffie-Hellman
Problem (CBDH)). Given (P,aP,bP, cP) ∈ G
4
1
for un-
known a, b, c ∈ Z
p
, the CBDH problem in (G
1
,G
2
)
is to compute ˆe(P,P)
abc
∈ G
2
. The advantage of any
probabilistic polynomial time algorithm A in solving
the CBDH problem in (G
1
,G
2
) is defined as:
Adv
CBDH
A
= Pr[A(P, aP,bP,cP) = ˆe(P,P)
abc
|a,b,c ∈
Z
p
]
The CBDH assumption is that, for any probabilistic
polynomial time algorithm A, the Adv
CBDH
A
is negli-
gibly small.
2.3 Generic Framework for PKI-based
Signature Scheme
The framework for a PKI based signature scheme
consists of the algorithms KeyGen, Sign, and Verify.
The algorithms are defined below:
KeyGen: takes a security parameter κ as input, and
outputs a private key sk and the corresponding public
key pk.
Sign: takes private key sk, public key pk and the
message m ∈ M as input. It outputs the signature σ.
Verify: takes signature σ, message m ∈ M and the
public key pk as input. It either accepts or rejects the
message claim to authenticity.
These algorithms must meet the standard consistency
constraint. For all (pk, sk) ←KeyGen and all m ∈ M ,
we have Verify = (pk, m, Sign (pk, sk,m)) = accept.
2.4 Security Model for PKI-based
Signature Scheme
Existential unforgeability is a standard acceptable no-
tion of security for signature schemes. We say that
any signature scheme is existentially unforgeable un-
der adaptive chosen message attacks if any polynomi-
ally bounded adversary A has negligible advantage in
the following game with the challenger C .
KeyGen: C runs the KeyGen algorithm and generates
the system parameters params and the secret key sk.
It gives params to A and keeps sk secret.
Training Phase: After the KeyGen phase is over, A
starts interacting with C by querying various oracles
provided by C in the following way:
• Random Oracle: A queries hash function listed
in params for any arguments, and C responds by
treating the hash function as a random function.
• Sign Oracle: A issues signature queries on mes-
sage m. Using sk, C runs the signing algorithm
and returns a resulting signature σ as response.
Additionally, C maintains a set W (W = {φ} ini-
tially) and when m is queried by A to the sign or-
acle, C updates W as W = W ∪ {m}.
Sign Forgery: On obtaining sufficient training, A
outputs a valid message-signature (m
∗
,σ
∗
) pair such
that the following two conditions hold: 1. Verify
(pk, m
∗
,σ
∗
) = accept, and 2. (m
∗
) /∈ W where W is
set of all messages queried by A in Sign Oracle.
The advantage of an adversary A in breaking the
chosen plaintext security of signature scheme is de-
fined as:
Adv
EU F−CMA
A
= Pr[A → (m
∗
,σ
∗
) : Verify
(pk, m
∗
,σ
∗
) = accept
V
(m
∗
) /∈ W ].
2.5 Generic Framework for ID-based
Encryption Scheme
An ID-based encryption scheme can be defined as a
tuple
h
S,K ,E, D
i
, where S is the setup algorithm,
K is the key extract algorithm, E is the encryption
algorithm, and D is the decryption algorithm. The
algorithms are defined as shown below:
Setup: takes a security parameter κ and returns
params (system parameters) and master key. Params
include a definition of finite message space M , and
a description of a finite ciphertext space C . Intu-
itively, params will be publicly known, while the mas-
ter key will be known only to the “Private Key Gener-
ator”(PKG).
Key Extract: takes params, master-key, and an arbi-
trary ID as input, and returns a private key d. Here
ID is the identity string that is used as a public key,
and d is the corresponding private decryption key. K
extracts a private key from the given public key.
Encrypt: takes params, ID, and M ∈ M as input. It
returns a ciphertext C ∈ C .
Decrypt: takes params, C ∈ C , and a private key d as
input. It returns M ∈ M .
These algorithms must satisfy the standard consis-
tency constraint. When d is the private key generated
by the Key Extract algorithm and corresponds to the
identity ID, the following should hold.
∀M ∈ M :Decrypt: (params,C,d) = M, where C=
Encrypt: (params, ID,M).
2.6 Security Model for ID-based
Encryption Scheme
Chosen plaintext security (IND-CPA) is the standard
SECRYPT2015-InternationalConferenceonSecurityandCryptography
254

acceptable notion of security for encryption schemes.
We say that an ID-based encryption scheme is seman-
tically secure against adaptive chosen plaintext attack
(IND-CPA) if any polynomially bounded adversary A
has negligible advantage in the following game with
the challenger C :
Setup: Challenger C runs the Setup algorithm. It
gives A the resulting system parameters params. It
keeps the master key msk to itself.
Phase I: A issues queries q
1
,q
2
,...,q
m
where q
i
is as
follows:
KeyExtract Query hID
i
i: C corresponds by running
KeyGen algorithm to generate the private key d
i
. It
sends d
i
to A. These queries may be asked adap-
tively i.e. each query q
i
may depend on the replies
to q
1
,q
2
,...,q
i−1
.
Challenge: A after getting sufficient training gives
two messages (m
0
,m
1
) of equal length, and an iden-
tity ID
∗
on which it wishes to be challenged to C.
C picks a random bit b ∈ {0,1} and sets the chal-
lenge ciphertext to C
∗
= Encrypt (params,ID
∗
,m
b
).
It sends C
∗
as a challenge to A.
Phase II: A is again allowed to get training after get-
ting the challenge ciphertext C
∗
. The only restriction
is that the private key of ID
∗
should not be queried to
the key extract oracle.
Guess: Finally, after getting training in Phase II, A
produces an educated guess b
0
∈ {0,1}. A wins if
b
0
= b. The advantage of A in breaking the chosen
plaintext security of an ID-based encryption system is
given by,
Adv
IND−CPA
A
= Pr[b
0
= b] −
1
2
.
3 BASIC SIGNATURE SCHEME
(Basic
Sign
)
We will now construct a secure public key signature
scheme in the random oracle model under the CDH
assumption. This signature scheme is weakly un-
forgeable, i.e. the adversary is not allowed to submit
as forgery a message signature pair for which mes-
sage it has already queried the signature oracle. This
is a PKI based signature scheme and this will be used
by the PKG to generate the private key for the users
of an ID-based encryption scheme.
User KeyGen: Let κ be the security parameter and
G
1
, G
2
be cyclic prime order groups of order p, where
G
1
is an additive group and G
2
is a multiplicative
group. Choose P, Q ∈
R
G
1
, and let ˆe : G
1
× G
1
→ G
2
be a bilinear map. To generate the key, user chooses
s ∈
R
Z
p
and computes the public key P
pub
= sP. The
user also chooses random values u
0
,u
1
.......u
k
∈ G
1
and a cryptographic hash function H
1
(.) defined by,
H
1
: {0,1}
n
→ {0,1}
k
Here k is a number typically of size 128 bits, to
ensure collision resistance against birthday attack.
And n is the size of message. The public key is

G
1
,G
2
,P, Q, p, ˆe,H
1
,P
pub
,u
0
,u
1
.....u
k

. The private
key of the user is
h
s
i
.
Sign: For generating the signature on message m ∈
{0,1}
n
by the user, this algorithm uses the private key
of the user and performs the following:
• Computes q
m
= H
1
(m) ∈ {0, 1}
k
. Here, q
m
repre-
sents a k-bit number. Let q
m
[i] represent the i
th
bit
of q
m
.
• Chooses random r
m
, ¯r
m
∈ Z
p
.
• Sets d
m
= sq
m
+ r
m
∈ Z
p
.
• Sets Y
m
= ¯r
m
P ∈ G
1
.
• Sets X
m
= r
m
Q + ¯r
m
(u
o
+
k
∑
i=1
q
m
[i]u
i
) ∈ G
1
.
• Outputs the signature σ = hd
m
,Y
m
,X
m
i.
Verify: Now, the generated signature can be verified
as follows:
• On receiving σ = hd
m
,Y
m
,X
m
i, compute q
m
=
H
1
(m) and r
m
P = d
m
P − q
m
(sP) = d
m
P −
q
m
(P
pub
).
• Check if ˆe(P, X
m
)
?
= ˆe(Y
m
, (u
0
+
k
∑
i=1
q
m
[i]u
i
))
ˆe(r
m
P, Q).
If the above check holds, return the signature as
“Valid” else return “Invalid”.
Correctness: If the signature is generated correctly,
then it will pass the verification test. In fact,
LHS= ˆe(P,X
m
) = ˆe(P, r
m
Q + ¯r
m
(u
0
+
k
∑
i=1
q
m
[i]u
i
))
= ˆe(P, r
m
Q) ˆe(P, ¯r
m
(u
0
+
k
∑
i=1
q
m
[i]u
i
))
= ˆe(r
m
P, Q) ˆe(¯r
m
P, (u
0
+
k
∑
i=1
q
m
[i]u
i
))
= ˆe(r
m
P, Q) ˆe(Y
m
, (u
0
+
k
∑
i=1
q
m
[i]u
i
))
= RHS
Remark. For generating the private keys of the users
of an ID-based system, a PKI based signature scheme
will be used by the PKG of the ID-based system. We
want our PKI based signature scheme to have the fol-
lowing properties:
PracticalIBESecureunderCBDH-EncryptingWithoutPairing
255

• In the signature scheme, the message hash should
not take any other parameters as input. Hence
Schnorr (Schnorr, 1989) type signature schemes
cannot be used for the purpose. In order to of-
fer existential unforgeability, Schnorr type signa-
ture schemes will always use hash functions of
the type H (message,randomness, ...). In fact, if
the hash function uses only the message as the
parameter, the signature scheme becomes forge-
able. Hence the hash function uses additional ran-
domness as an input parameter. However such
schemes if used by a PKG, leads to inefficient ID-
based encryption schemes.
• Our second goal is to avoid Full Domain Hash
function and hence we make use of a computa-
tion similar to Waters’ hash function. Hence the
BLS (Boneh et al., 2004) type signatures which
use FDH cannot be used for our purpose.
Since none of the existing key constructs are suit-
able for our purpose, we have come up with a novel
key construct. Although, unlike Schnorr signature
scheme, our scheme uses only message as the input to
the hash, still our scheme is secure because we have
bound the randomness r
m
and hash H
1
in other com-
ponents of the signature through a computation simi-
lar to Waters’ hash.
Theorem 1: If there exists an EUF-CMA adversary
for our Basic
Sign
scheme with a non-negligible prob-
ability, then we show that there exists a challenger
C who can solve the Computational Diffie-Hellman
problem (CDHP) on G
1
with almost the same proba-
bility.
4 CONSTRUCTION OF A CPA
SECURE ENCRYPTION
SCHEME
In this section we propose a novel ID-based encryp-
tion scheme without using bilinear pairing during
encryption and prove the security in random oracle
model, assuming the hardness of Computational Bi-
linear Diffie-Hellman Problem (CBDHP). The PKG
of this scheme uses Basic
Sign
signature scheme ex-
plained in the previous section to generate private key
of the user. The details of the new scheme and the
formal proof is given below.
4.1 The Scheme (Γ-Scheme)
Setup: Let κ be the security parameter and G
1
,
G
2
be cyclic prime order groups of order p, where
G
1
is an additive group and G
2
is a multiplicative
group. Let P,Q ∈
R
G
1
be the elements of G
1
, and
ˆe : G
1
× G
1
→ G
2
be a bilinear map. PKG chooses
s ∈
R
Z
p
and computes the public key P
pub
= sP. PKG
also sets α = ˆe (P,Q) , α
1
= ˆe(P, Q)
s
. Additionally,
PKG chooses random values u
0
,u
1
.......u
k
∈ G
1
and
picks two cryptographic hash functions H
1
(.), and
H
2
(.) defined by,
H
1
: {0,1}
n
→ {0,1}
k
, and H
2
: G
2
→ {0,1}
n
Here k is a number typically of size 128
bits, to ensure collision resistance against
birthday attacks. And n is the size of iden-
tity. The system parameters params are

G
1
,G
2
,P, Q, p, ˆe,H
1
,H
2
,P
pub
,α,α
1
,u
0
,u
1
.....u
k

.
The master private key is
h
s
i
.
Key Extract. Given the master private key s, and the
user identity ID
A
∈
{
0,1
}
n
, the algorithm does the fol-
lowing:
1. Computes q
A
= H
1
(ID
A
) ∈ {0, 1}
k
. Here, q
A
rep-
resents a k-bit number. Let q
A
[i] represent the i
th
bit of q
A
.
2. Chooses random r
A
, ¯r
A
∈ Z
p
.
3. Sets d
A
= sq
A
+ r
A
∈ Z
p
.
4. Sets Y
A
= ¯r
A
P ∈ G
1
.
5. Sets X
A
= r
A
Q + ¯r
A
(u
o
+
k
∑
i=1
q
A
[i]u
i
) ∈ G
1
.
6. Outputs the private key of the user as D
A
=
hd
A
,Y
A
,X
A
i.
Note. The Key Extract algorithm is a probabilistic
polynomial time (PPT) algorithm. However, this al-
gorithm can be made deterministic by generating the
random coins r
A
, ¯r
A
through a pseudo random func-
tion with the identity and the master private key as
the seeds (Pornin, 2012).
Encryption. On input of a message m ∈ M and iden-
tity ID
A
∈
{
0,1
}
n
, the encrypt algorithm works as fol-
lows:
• Chooses r ∈
R
Z
p
.
• Computes c
1
= rP and β = α
rq
A
1
.
• Computes c
2
= r(u
o
+
k
∑
i=1
q
A
[i]u
i
).
• Computes c
3
= H
2
(β) ⊕ m.
• Outputs the ciphertext C = hc
1
,c
2
,c
3
i.
Decryption. Let C = hc
1
,c
2
,c
3
i be a valid encryption
of m under the identity ID
A
. Then C can be decrypted
using the private key D
A
as follows:
1. Compute β
0
= ˆe(c
1
,d
A
Q − X
A
) ˆe (Y
A
, c
2
).
SECRYPT2015-InternationalConferenceonSecurityandCryptography
256

2. Compute m = H
2

β
0

⊕ c
3
.
Correctness: It can be shown that β
0
= β as follows:
β = α
rq
A
1
β
0
= ˆe(c
1
,d
A
Q − X
A
) ˆe(Y
A
, c
2
)
= ˆe(c
1
,d
A
Q) ˆe(c
1
,−X
A
) ˆe(¯r
A
P, r(u
0
+
k
∑
i=1
q
A
[i]u
i
))
= ˆe (rP, (sq
A
+ r
A
)Q) ˆe(rP, r
A
Q + ¯r
A
(u
0
+
k
∑
i=1
q
A
[i]u
i
))
−1
ˆe(¯r
A
P, r(u
0
+
k
∑
i=1
q
A
[i]u
i
))
= ˆe(rP, sq
A
Q) ˆe(rP, r
A
Q) ˆe(rP, r
A
Q)
−1
ˆe(rP, ¯r
A
(u
0
+
k
∑
i=1
q
A
[i]u
i
))
−1
ˆe(¯r
A
P, r(u
0
+
k
∑
i=1
q
A
[i]u
i
))
= ˆe(P, Q)
srq
A
= α
rq
A
1
= β
Theorem 2. If there exists an IND-CPA adversary for
our scheme Γ with a non-negligible probability then
it is possible to construct another algorithm which
can solve the Computational Bilinear Diffie-Hellman
problem (CBDHP) with almost the same probability.
5 IND-CCA SECURE SCHEME
We apply the Fujisaki Okamoto Transformation (Fu-
jisaki and Okamoto, 2013) to convert the IND-CPA
secure Γ scheme of the previous section into an adap-
tive chosen ciphertext secure ID-based scheme in the
random oracle model. We obtain the following IBE
scheme which we call the Γ
0
scheme.
5.1 The Scheme

Γ
0
− scheme

Setup : The Setup is similar to Γ scheme. In
addition, we pick a hash function H
3
(.) defined as,
H
3
: {0,1}
n
× {0, 1}
ρ
→ Z
p
. And, redefine the hash
function H
2
(.), as H
2
: G
2
→ {0,1}
n+ρ
. Remember
that ρ is a number typically of size 128 bits.
Key Extract. As in Γ scheme.
Encryption. On input of a message m ∈ {0, 1}
n
and
identity ID
A
, the encrypt algorithm works as follows:
• Chooses ω ∈ {0,1}
ρ
and computes
r = H
3
(m||ω) ∈ Z
p
.
• Computes c
1
= rP ∈ G
1
and β = α
rq
A
1
.
• Computes c
2
= r(u
o
+
k
∑
i=1
q
A
[i]u
i
) ∈ G
1
.
• Computes c
3
= H
2
(β) ⊕ (m||ω).
• Output the ciphertext C = hc
1
,c
2
,c
3
i.
Decryption. Let C = hc
1
,c
2
,c
3
i be a valid encryption
of m under the identity ID
A
. Then C can be decrypted
by the user as follows:
• Computes β
0
= ˆe(c
1
,d
A
Q − X
A
) ˆe (Y
A
, c
2
).
• Computes (m
0
||ω
0
) = H
2

β
0

⊕ c
3
.
• Compute r
0
= H
3
(m
0
||ω
0
).
• Test that c
1
= r
0
P and c
2
= r
0
(u
0
+
k
∑
i=1
q
A
[i]u
i
).
If the above two tests hold, output m
0
as the decryption
of C.
Correctness: It can be easily shown that m
0
= m since
β
0
= β. The proof of correctness follows from that of
Γ scheme.
Remark. Let Γ be an IND-CPA secure ID-based
encryption scheme. Then after applying Fujisaki
Okamoto transformation (Fujisaki and Okamoto,
2013) to Γ, we get an IND-CCA secure ID-based en-
cryption scheme Γ
0
under the same assumption that
CBDH is hard to solve in (G
1
,G
2
). This statement
follows from the proof of standard transformation due
to Fujisaki Okamoto for converting an IND-CPA se-
cure scheme to IND-CCA secure scheme.
6 CONCLUSION
In this paper, we have designed a novel identity based
encryption scheme in random oracle model which re-
duces to the well known CBDH problem. Our scheme
differs from all existing schemes because it does not
use full domain hash and it does not employ pairing
computation during encryption process, thus making
it more efficient. In order to achieve these proper-
ties, we have proposed a novel PKI based signature
scheme, which is used to extract the private key of
the identity based encryption scheme. We have first
proved the security of our scheme in CPA security
notion, and then using Fujisaki Okamoto transforma-
tion we have proposed the CCA secure version of our
scheme. Ours is the only scheme which does not
use bilinear pairing during encryption without com-
promising on security. Our scheme is proven secure
under the well known CBDH problem.
REFERENCES
Agrawal, S., Boneh, D., and Boyen, X. (2010). Efficient
lattice (h)ibe in the standard model. In Advances in
PracticalIBESecureunderCBDH-EncryptingWithoutPairing
257

Cryptology - EUROCRYPT, volume 6110 of Lecture
Notes in Computer Science, pages 553–572. Springer.
Attrapadung, N., Furukawa, J., Gomi, T., Hanaoka, G.,
Imai, H., and Zhang, R. (2007). Efficient identity-
based encryption with tight security reduction. IEICE
Transactions, 90-A(9):1803–1813.
Barreto, P. S. L. M., Libert, B., McCullagh, N., and
Quisquater, J.-J. (2005). Efficient and provably-secure
identity-based signatures and signcryption from bilin-
ear maps. In Advances in Cryptology - ASIACRYPT,
volume 3788 of Lecture Notes in Computer Science,
pages 515–532. Springer.
Boneh, D. and Boyen, X. (2011). Efficient selective
identity-based encryption without random oracles.
Journal of Cryptology, Vol 24(No 4):659–693.
Boneh, D. and Franklin, M. K. (2005). Identity-based en-
cryption from the weil pairing. In Advances in Cryp-
tology - CRYPTO, volume 2139 of Lecture Notes in
Computer Science, pages 213–229. Springer.
Boneh, D., Lynn, B., and Shacham, H. (2004). Short sig-
natures from the weil pairing. Journal of Cryptology,
Vol 17(No 4):297–319.
Chen, L. and Cheng, Z. (2005). Security proof of sakai-
kasahara’s identity-based encryption scheme. In IMA
Int. Conf., pages 442–459.
Fujisaki, E. and Okamoto, T. (2013). Secure integration
of asymmetric and symmetric encryption schemes. J.
Cryptology, 26(1):80–101.
Galindo, D. and Garcia, F. D. (2009). A schnorr-
like lightweight identity-based signature scheme. In
Progress in Cryptology - AFRICACRYPT, volume
5580 of Lecture Notes in Computer Science, pages
135–148. Springer.
Gentry, C. (2006). Practical identity-based encryption with-
out random oracles. In Advances in Cryptology - EU-
ROCRYPT, volume 4004 of Lecture Notes in Com-
puter Science, pages 445–464. Springer.
Herranz, J. (2006). Deterministic identity-based signatures
for partial aggregation. Comput. J., 49(3):322–330.
Islam, S. K. H. and Biswas, G. P. (2012). A pairing-
free identity-based authenticated group key agreement
protocol for imbalanced mobile networks. Annales
des T
´
el
´
ecommunications, 67(11-12):547–558.
Katz, J. and Wang, N. (2003). Efficiency improvements for
signature schemes with tight security reductions. In
ACM Conference on Computer and Communications
Security, pages 155–164.
Kiltz, E. (2006). Chosen-ciphertext secure identity-based
encryption in the standard model with short cipher-
texts. IACR Cryptology ePrint Archive, 2006:122.
Pornin, T. (2012). Deterministic Usage of DSA
and ECDSA Digital Signature Algorithms.
urlhttp://tools.ietf.org/id/draft-pornin-deterministic-
dsa-01.html#rfc.section.3.
Sakai, R. and Kasahara, M. (2003). Id based cryptosystems
with pairing on elliptic curve. IACR Cryptology ePrint
Archive, 2003:54.
Schnorr, C.-P. (1989). Efficient identification and signa-
tures for smart cards. In Advances in Cryptology -
CRYPTO, volume 435 of Lecture Notes in Computer
Science, pages 239–252. Springer.
Selvi, S. S. D., Vivek, S. S., and Rangan, C. P. (2011).
Identity-based deterministic signature scheme with-
out forking-lemma. In Advances in Information and
Computer Security - IWSEC, volume 7038 of Lecture
Notes in Computer Science, pages 79–95. Springer.
Shamir, A. (1984). Identity-based cryptosystems and sig-
nature schemes. In CRYPTO - 84, Lecture Notes in
Computer Science, pages 47–53. Springer.
Waters, B. (2005). Efficient identity-based encryption with-
out random oracles. In Advances in Cryptology - EU-
ROCRYPT 2005, volume 3494 of Lecture Notes in
Computer Science, pages 114–127. Springer.
SECRYPT2015-InternationalConferenceonSecurityandCryptography
258