Contrast-to-Noise based Metric of Denoising Algorithms

for Liver Vein Segmentation

A. Nikonorov

1,2

, A. Kolsanov

, M. Petrov

1,2

, Y. Yuzifovich

, E. Prilepin

and K. Bychenkov

Samara State Aerospace University, Moskovskoe shosse 34, Samara, Russia

Image Processing Systems Institute, Russian Academy of Science, Molodogvardeyskaya st. 151, Samara, Russia

Samara State Medical University, Chapaevskaya st. 89, Samara, Russia

SmedX, LLC, Moskovskoe shosse 34, Samara, Russia

Keywords: Contrast to Noise Ratio, Total Variance De-noising, Liver, Vessels Segmentation, CUDA, GPGPU, Xeon

Phi, Proximal Algorithms, Fast Marching, Geodesic Active Contours.

Abstract: We analyse CT image denoising when applied to vessel segmentation. Proposed semi-global quality metric

based on the contrast-to-noise ratio allowed us to estimate initial image quality and efficiency of denoising

procedures without prior knowledge about a noise-free image. We show that the total variance filtering in L1

metric provides the best denoising when compared to other well-known denoising procedures such as non-

local means denoising or anisotropic diffusion. Computational complexity of this denoising algorithm is

addressed by comparing its implementation for Intel MIC and for NVIDIA CUDA HPC systems.

1 INTRODUCTION

Liver volumetry is a critical aspect of safe hepatic

surgeries. Precise segmentation of the vessel tree

structure topology can be used in an image-guided

surgery for liver lobes segmentation, tumor detection,

and to reduce incisions and prevent post-operative

bleeding, resulting in less blood loss and rapid patient

recovery. CT image quality varies widely in different

tomograms. Image noise and low contrast between

veins and surrounding tissue make automatic and

semi-automatic intrahepatic blood vessel

segmentation a challenging task.

Radiation dose from clinical CT scanning is an

increasing health concern worldwide (Brenner and

Hall, 2007). The guiding principle in CT scanner

design is to reduce radiation levels as much as

possible while maintaining acceptable diagnostic

accuracy. This results in stronger image noise. Most

noise suppression techniques in CT images can be

broadly categorized as projection space denoising,

image space denoising, and iterative reconstruction

(Li et al., 2014). Denoising is critical for the tasks of

vascular structure segmentation.

Low contrast problem is caused by non-optimal

distribution of the contrast agent during the scan. For

example, in venous phase the agent may still be

present in liver veins while absent in inferior vena

cava. Low contrast in noisy images makes vessel

structures indistinguishable from surrounding tissue.

Differences in CT image quality affects

segmentation results, and new segmentation methods

have been suggested (Shang, 2010). Multiple

methods exist to perform image restoration both at the

scanning and reconstruction stages (Shuman et al.,

2014), and at the image processing stage (Brenner and

Hall, 2007).

Quality measure is important for both image and

segmentation quality evaluation. However, there is no

unambiguous solution to measure image quality in

practical CT segmentation tasks. To use a common

PSNR measure we need to have a noise-free image

available. Contrast-to-noise measures require a ROI

in the image to be selected (Shuman et al., 2014). This

prior knowledge is available only for synthetic tests

or when we already have a “ground truth”

segmentation.

We propose a new contrast-to-noise-based

measure with reduced dependency on the prior

knowledge, and proceed to use this measure to test

different denoising algorithms applied to vessel

segmentation. Incremental vessel segmentation

technique is based on fast marching and level-set

algorithms.

Total variance in L1 distance (Chambolle and

Pock, 2011) shows the best denoising quality. To

make this computational-intensive method practical,

Nikonorov A., Kolsanov A., Petrov M., Yuzifovich Y., Prilepin E. and Bychenkov K..

Contrast-to-Noise based Metric of Denoising Algorithms for Liver Vein Segmentation.

DOI: 10.5220/0005542400590067

In Proceedings of the 12th International Conference on Signal Processing and Multimedia Applications (SIGMAP-2015), pages 59-67

ISBN: 978-989-758-118-2

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

we implemented this denoising procedure using two

“desktop supercomputing” methods: GPGPU using

NVIDIA CUDA and MIC (Many Integrated Core)

using Intel Xeon Phi.

2 ONE POINT

CONTRAST-TO-NOISE RATIO

AS A QUALITY MEASURE

Most of quality measures developed for signal and

image processing, such as PSNR and method noise

(Buades, Coll and Morel, 2006), require prior

knowledge about a noise-free image. For example,

CT reconstruction quality for different radiation dose

is investigated using phantom images (Shuman et al.,

2014), (Hendrick, 2008). These metrics measure

different aspects of image quality: PSNR describes

degradation of the best signal, while method noise

measures image edge corruption by denoising

procedures. The most important image quality aspect

for vessel segmentation is a contrast between vessels

and noisy surrounding tissue.

According to (Hendrick, 2008), contrast-to-noise

ratio (CNR) is defined as the ratio of signal difference

(contrast) to the noise level in the image:

object background

CNR

−

(1)

where

object

and

background

are average intensities

of the object and its background,

is standard

deviation of the image noise.

Details of CNR estimation vary across different

works. Usually, it is necessary to choose one ROI on

the object and one – on the background to compute

object

and

background

(Shuman et al., 2014),

(Magnotta and Friedman, 2006). However, it is

possible to get incorrect CNR estimation on non-

uniform image parts (Mori et al., 2013).

In (Nikonorov et al., 2014), Sliver7 (Heimann et

al., 2009) training database was used to estimate

denoising quality. The training set contains

segmented livers and these segmentations are used to

estimate

object

in (1) and an outside image part is

used for

background

estimation. Unfortunately, this

prior knowledge is not available for segmentation

tasks found in many preoperative planning situations.

We will use the following image model to

estimate CNR on real CT data. We assume that the

image consists of only two components: a vessel of a

certain unknown diameter that we need to estimate,

and surrounding tissue. This enables us to apply

bimodal intensity distribution hypothesis at any local

neighborhood.

We used two approaches for CNR-like measure

computation. In the simple two-point method we use

one point inside and one outside of the vessel object

to be segmented. Similar to ROI selection in (Shuman

et al., 2014), a two-point CNR has the following

form:

1,2,3

(, ) (, )

(, ) ,

(, )

p( ), : , ,

,maxxx

obj obj bkg bkg

obj bkg

bkg bkg

obj obj

MRMR

∞

−





≤









=−









xxx x

(2)

where

obj

x и

bkg

x are points at the vessel and

surrounding tissue,

x, 1,2,3

i =

-th component

x ,

()x is an intensity value at the point x , M is

an intensity median over a cubic neighborhood,

obj

is the size of the cubic neighborhood on the vessel

(object),

bkg

R – on the surrounding tissues

(background),

(, )

bkg bkg

MRx

is defined the same way

(, )

obj obj

MRx

(, )

bkg bkg

is standard deviation

across the same region as

bkg

∞

is L

∞

Chebyshev distance.

Computation of

obj

R could be done assuming

unimodality of the intensity distribution in the cubic

image patch centered in

obj

x . Follow (Basu and Das-

Gupta, 1992) if the distribution is unimodal then

3/5,

obj obj

obj

−

≤

(3)

obj obj

obj

−

≤

(4)

where

obj

is mean estimation and

obj

mode

estimation over the image cubic neighborhood

centered in

obj

x .

With

obj

R increasing above a threshold, the

distribution loses its unimodality and inequalities (3)

and (4) fails.

To separate the object from the background the

value of (2) must be greater than 1, with a value of 2

being a better threshold for stable separation of the

vessel from its surroundings. These values are

obtained in the experiments, described in section 6.

Values of (2) vary along with the point on the

background selection. A low value for (2) means that

the segmentation quality will be subpar, but if we get

SIGMAP2015-InternationalConferenceonSignalProcessingandMultimediaApplications

good value then it does not follow that quality will be

high. It would only mean that we have not found a

bad case, yet. Therefore, the value of metric (2) is

necessary but not sufficient for good vessels

separation from background.

We propose a semi-global method for CNR-like

measure estimation using only one point inside the

object. We use a cubic neighborhood of the point

obj

defined using

∞

as done in (2):

{

}

:, .

obj

∞

=≤xx x

(5)

The distribution inside the cube is unimodal. The

tissue surrounding this cube has different intensity

distribution and thus overall distribution becomes

bimodal, so inequalities (3), (4) fail and take the

following form:

3/5

bkg obj

obj

−

(6)

bkg obj

obj

−

(7)

At least one of (6), (7) must be true if the distribution

isn’t unimodal. We can estimate the median over the

set of cubic patches centered in

and having the

size

bkg

, all the patches placed in the neighborhood

D of the

obj

point:

{}

p( ) : ,

()

kbkg

bkg obj

obj k

∞

≤







 



 



 







xxx

(8)

The

{

}

set includes only patches with either (6)

or (7) to be true, so it is an estimation of the

background intensity median. The standard deviation

for these patches is estimated as follows:

{}

p( ) : ,

()

kbkg

bkg obj

obj k

σσ

∞







≤

 



 



≤

 







xxx

(9)

Finally, we estimate median and standard deviation

as modes of (8) and (9). So, semi-global CNR-like

measure takes the following form:

()mode( ())

()

(mode( ( )) ) / 2

obj bkg obj

obj

bkg obj obj

σσ

−

(10)

The variance of the noise often depends on the signal

intensity, with the object and the background

producing different estimates for the variance. As a

result, it is not clear which variance must be used in

the denominator of the measure (1). To address this

problem, we use a half sum of the object and

background variances in the denominator of the

proposed one-point contrast-to-noise measure (10) as

a compromise.

3 VESSELS SEGMENTATION

TECHNIQUE

We applied Level Sets approach to segment vessels.

Semi-automatic segmentation is performed in two

steps. At the first “interactive initialization” step, Fast

Marching Upwind Gradient method is used for the

rough segmentation of vascular structures. At the

second “precise segmentation” step, Geodesic Active

Contours method is used for the final segmentation of

vascular structures. The algorithm is shown in Fig. 1

(Antiga, 2002), (Caselles, Kimmel, and Sapiro,

1997).

At the first step, seed points and optional target

points are specified inside the vessel to be segmented.

Seed points indicate the start of the wave front

propagation in the Fast Marching algorithm.

The wave propagation stops when one of the

specified target points is reached. The wave front

propagation is determined by a speed image. The

original image has been used as a speed image after

applying a threshold.

At the second step, we use Geodesic Active

Contour method to refine segmentation. This method

requires two inputs: The Fast Marching result as the

initial level set, and the feature image. We use the

gradient magnitude of the original image with the

transformation of the nonlinear function (Sigmoid

filter) as the edge potential map.

The level-set algorithm produces a real-valued

image. The binary image, obtained by applying a

threshold, is the final segmentation result.

We also used a restricted segmentation region

defined by a binary image of an organ or an organ

region to improve segmentation speed and increase

segmentation precision.

We used stepwise incremental approach to

segment the whole vascular tree when it was

impossible to perform vascular tree segmentation at

once. Each step implies the segmentation of a certain

vessel subtree. The final binary image obtained at

each step is combined with the final binary images

achieved at previous steps.

To improve segmentation quality in low-contrast

situations, the original image has been smoothed by

Gaussian filter to prevent the leak into the region rich

in blood vessels represented as less than one pixel

diameter on low-contrast CT data.

Contrast-to-NoisebasedMetricofDenoisingAlgorithmsforLiverVeinSegmentation

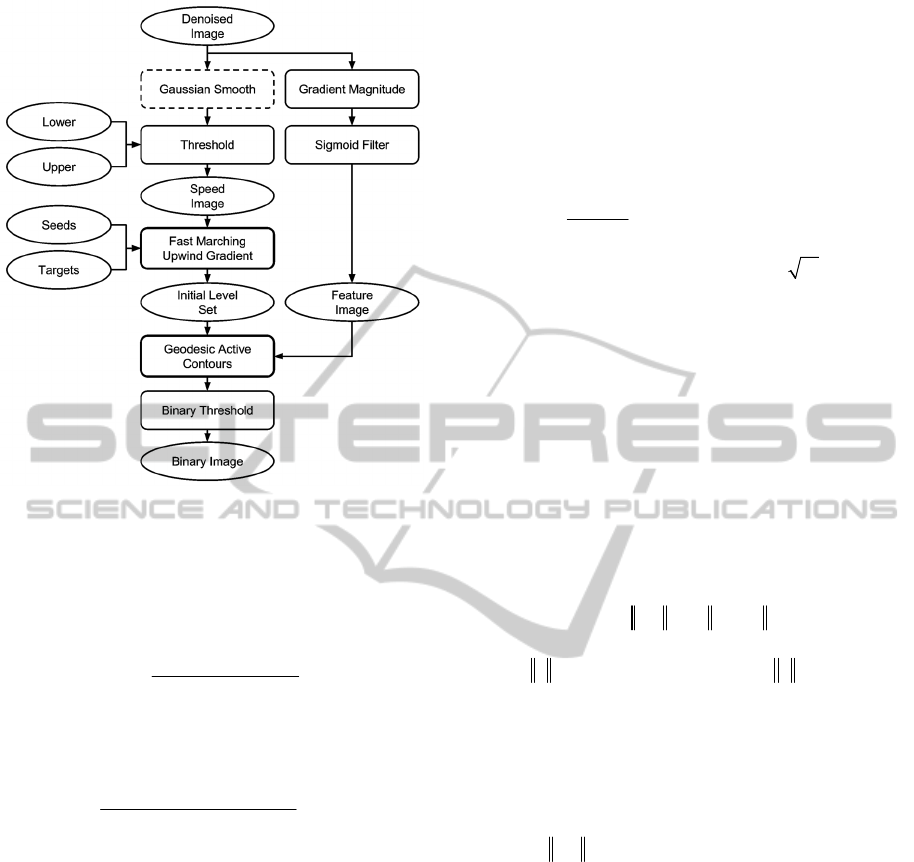
Figure 1: Incremental segmentation algorithm.

The main parameter of the algorithm is a

threshold between vessels and surrounding tissues.

We automatically estimate its value by using a

Mahalanobis-like procedure:

()

obj bkg bkg

bkg

bkg obj

σσ

−

(11)

and using measure (10):

mode( ( ))

()mode( ())

bkg obj

obj bkg obj

(12)

where

is a threshold value, and

()

obj

is defined

by (10).

4 DENOISING PROCEDURES

We compared four denoising techniques applied to

vessel segmentation: curvature anisotropic diffusion,

bilateral filtering, non-local-means filter, and total

variance based denoising in

and

We will briefly describe these methods using the

following notation. Let us denote a noisy source

image as

()x

, while the target filtered image as

()x

The downside of image denoising (smoothing) is

that it blurs sharp boundaries used to distinguish

anatomical structures, such as vessels. Perona and

Malik (1990) introduced an alternative to linear-

filtering called anisotropic diffusion. The motivation

for anisotropic diffusion (also called nonuniform or

variable conductance diffusion) is that a Gaussian

smoothed image is a single time slice of the solution

to the heat equation that has the original image as its

initial conditions. Thus, the solution to

(,)

∂

=∇⋅∇

∂

(13)

where ( , 0) ( )

=xpx is

(,) G( 2) ()gt t p=⊗xx

and G( )

is a Gaussian kernel with standard

deviation

. Anisotropic diffusion includes a

variable conductance term which in turn depends on

the differential structure of the image. Thus, the

variable conductance can be formulated to limit edge

smoothing in images, as measured by a high gradient

magnitude, for example. In our work, we use

curvature anisotropic diffusion modification,

described in (Shang, 2010) and implemented in ITK

(Johnson et al., 2013).

Total variation model was invented by Rudin,

Osher, Fatemi (1992). This model is based on

minimization of the following functional

arg min

=∇+−

pppp

(14)

where

is the robust

norm,

is the

norm used in the least-squares restoration model,

is the source noisy image,

is the target filtered

image and

is the weighting parameter, which

defines the trade-off between regularization and data

fitting. The

norm of the image gradient is total

variation

∇p

. This filtering is capable of denoising

images without blurring edges. We use

implementation of total variance filtering based on

(Chambolle and Pock, 2011). We will refer to it as

TV L2 de-noising.

An alternative denoising technique, based on non-

local-mean approach proposed in (Buades, Coll and

Morel, 2006), involves averaging over pixels similar

in intensity but distant in spatial domain. It is

therefore necessary to scan a vast portion of the image

in search of all the pixels that resemble the pixel to

denoise because the image can have periodic textured

patterns, or the elongated edges. Denoising is then

done by computing the average color of these most

resembling pixels. The resemblance is evaluated by

comparing a whole window around each pixel. This

new filter is called non-local means and is computed

as follows:

SIGMAP2015-InternationalConferenceonSignalProcessingandMultimediaApplications

() (,) ()

()

pwp



xxyy

(15)

The family of weights

(, )w xy depends on the

similarity between the pixels

x and

, ()C x is a

weighting constant:

(N( ), (N( ))

(, ) exp





=−





(16)

where

()x denotes a square neighborhood of a

fixed size and centered around a pixel

x .

Another filtering method we test is a bilateral or

Yaroslavsky filter, which we use from ITK package

(Johnson et al., 2013).

This approach was previously compared to the

anisotropic diffusion and total variance filtering in

(Buades, Coll and Morel, 2006) using method noise

measure and comparing visual quality. The main idea

of the method noise measure is to estimate how a

denoising algorithm alters structures found in the

image.

We developed optimization method to de-noise

3D CT data based on the optimal first-order primal-

dual framework by Chambolle and Pock (2011). It is

a total variance minimization based on

norm, we

will call this method TV L1 denoising.

Let X and Y be the finite-dimensional real vector

spaces for the primal and dual space, respectively.

Consider the following operators and functions:

:X Y→K

is a linear operator from X to Y;

:X [0, )→+∞G is a proper, convex, (l.s.c.)

function;

:Y [0, )→+∞F is a proper, convex, (l.s.c.)

function;

where l.s.c. stands for lower-semi-continuous.

The optimization framework (Chambolle and

Pock, 2011) considers general problems in the

following form:

arg min ( ( )) ( ).=+

xFKxGx

(17)

To solve this problem, the following algorithm is

described in the paper (Chambolle and Pock, 2011).

During initialization,

, R

τσ

∈

are set,

[0,1]

∈

(, )XY∈×xy

is some initial approximation,

=xx. For 3D CT data, the final result obtained on

the previous slice is used as the initial approximation

for the next slice. With

0n ≥

as the current step

number, values of the

nnn

x are iteratively

updated as follows:

()

nFnn

prox

=+yyKx,

(18)

()

nnn

prox

xxKy

(19)

11 1

()

nn nn

++ +

=+ −xx xx.

(20)

The proximal operator with respect to G in (19), is

defined as:

() ( ) ()

arg min ( ),

prox

−

=+∂ =

=−+

xEGx

xx Gx

(21)

where E is an identity matrix. The proximal operator

(18) is defined in a similar way.

The model of denoising is based on the total

variance approach (Chambolle and Pock, 2011) and

is described by the following functional:

min

=∇+ −

pppp,

(22)

where

is the robust

norm,

p is the source

noisy image,

is the target filtered image and

the weighting parameter, which defines the tradeoff

between regularization and data fitting.

In order to apply the described algorithm to (22),

we follow the (Chambolle and Pock, 2011):

()G =∇

(23)

()F =−

ppp

(24)

Finally, proximal operators for steps (18) and (19)

of the algorithm can be obtained using (23) and (24).

Please refer to (Chambolle and Pock, 2011) for

further details. The denoising algorithm based on

total variance can preserve sharp edges. Also, the use

makes it possible to efficiently remove strong

outliers.

5 HIGH PERFORMANCE

IMPLEMENTATION OF

DENOISING ALGORITHM

As can be seen in the results of our experiments in the

following Section 6, TV L1 denoising algorithm

proved to be the best for low-contrast CT data, but it

is the most computationally expensive one. This is

why we implemented it for two many-core systems,

Xeon Phi and CUDA. The work (Pock et al., 2008)

addressed CUDA implementation of TV L1

algorithms, but did not provide details.

A general algorithm is shown in Fig. 2. The

implementation is based on (11)-(13). Expressions

(11)-(12) describe the dual part of the iteration of the

Contrast-to-NoisebasedMetricofDenoisingAlgorithmsforLiverVeinSegmentation

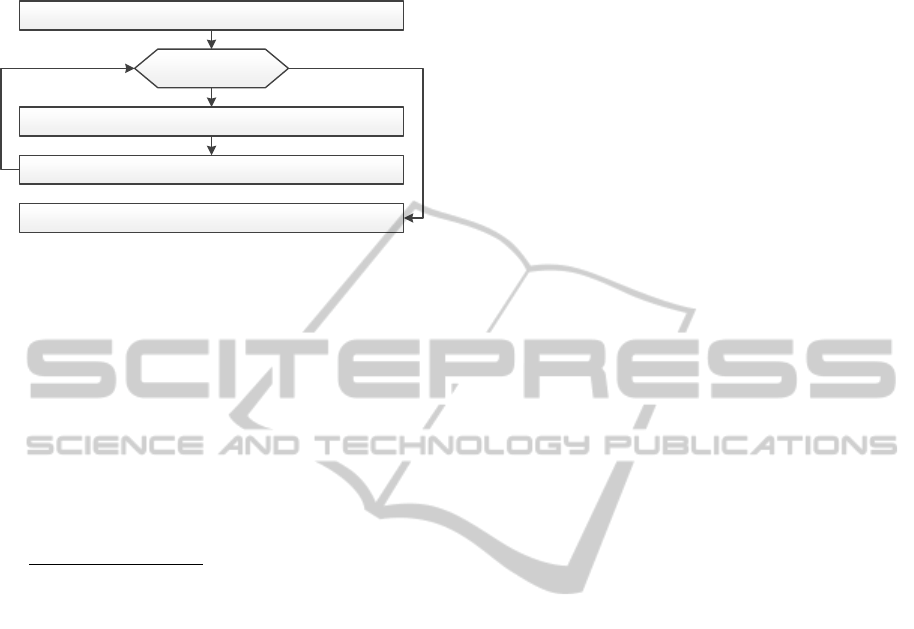
proximal algorithm, UpdateDual(), and (13)

describes the primal part UpdatePrimal().

Figure 2: General algorithm of TV L1 filtering.

TV L1 is based on proximal algorithms, these

algorithms have large dimensionality but they are

separable, as it was shown in (Parikh and Boyd,

2013). This property enables efficient parallel

implementation.

Each iteration of the computation is divided into

two stages: UpdateDual() and UpdatePrimal(). Inside

these stages we have a vector-like processing of the

arrays with a size of about 2

. However, these two

stages are sequential and require synchronization

between them at each iteration.

GPU implementation. Intensive memory use of

TV L1 algorithm represents a challenge for GPU

implementation. The size of the shared memory is a

major constraint of the GPU, which can be expressed

as follows:

max

max max

MP MP S MP

Th per MP MP B Th per MP

MP MP

opt

B Th per MP MP

SNNS

NNNN

NN N

=⋅≤

≤

(25)

where

S amount of available shared memory per

MP in bytes,

N - a number of blocks per MP,

necessary amount of shared memory per block,

max

– maximum amount of shared memory per MP in

bytes,

Th per MP

- a number of simultaneous threads

per MP,

N - a number of threads per block,

max

Th per MP

- maximum amount of threads per MP,

max

- a number of blocks per MP,

opt

- an optimal

block size in bytes.

In our case,

(1)

SB type

NN S=+⋅

, where

type

the size of pixel in bytes. So, the amount of shared

memory per multiprocessor is:

max

(1)

PMPB typeMP

SNN SS=⋅+⋅≤

(26)

For both tested GPU platforms we use

max

N =

max

2048

Th per MP

N =

max

49152

S =

, so,

128

opt

N =

threads per block. Finally, 8256

S =

bytes for single precision and

16512

S = bytes for

double precision, which is lower than

max

We use two CUDA kernel calls for each iteration.

The first kernel call implements UpdateDual(), the

second – UpdatePrimal(). There is global memory

exchange between these two kernel calls, that is why

we do not have any overhead caused by shared

memory invalidation between the kernel calls.

Many-core Xeon Phi implementation is an

alternative to CUDA. We use OpenMP for both

multicore CPU and Xeon Phi implementation. For

Xeon Phi we used non-shared memory offload model.

We use

omp parallel for private pragmas for the

CPU version. All intermediate variables are made

private. Synchronization by

omp barrier pragmas is

made after UpdateDual() and UpdatePrimal(), at

the

same places as in the CPU version. Private variables

are also the same as in the CPU version.

Main algorithm iteration loop and all inner loops

are made on the coprocessors side. Parallelization of

the for-loops is made by

omp parallel for simd private

pragma. The

simd modifier allows efficient utilization

of the Xeon Phi vectorized architecture. We bind

OpenMP threads to physical processing units by

setting environment variables KMP_AFFINITY to

"balanced,granularity=fine" and

KMP_PLACE_THREADS to "59C,4T".

We use one CT slice to test performance, with 600

iterations. The slice is 16-bit image of the 512х512

size. Testing equipment: Intel Xeon E5-2695 v2, Intel

Core i7 4770K at 4.2 GHz, Intel Xeon Phi 5110P,

NVIDIA Tesla K20m, NVIDIA GTX770 4096 MB.

In the offload model one core of Xeon Phi is reserved

for system need, which leaves us with 236 threads out

of 240 available at Xeon Phi. Results are shown in

Fig. 3.

As shown in Fig. 3, NVIDIA Tesla slightly

outperforms Intel Xeon Phi, with both systems about

10 times faster than a CPU-based version, and only

slightly faster than an implementation based on an

inexpensive GTX 770 GPU. A major advantage of

Xeon Phi is its capability to run the same OpenMP

implementation as a CPU-based version, which

makes Xeon Phi a better option for rapid prototyping

of computationally-expensive algorithms. GPGPU

approach is optimal for production use, when the cost

and power consumption are more important

considerations. With a typical CT that has about 200

slices, the data could be filtered by a GTX 770-based

system in about 3.3 seconds, which is acceptable for

UpdatePrimal(): <in: p; out: head_u; inout: u>

Writing filtered image

UpdateDual(): <in: head_u; out: p>

Reading image: <u = imageIn, head_u = u, p = zeros()>

i = 0:iterCount

SIGMAP2015-InternationalConferenceonSignalProcessingandMultimediaApplications

production use. Peak memory usage is one gigabyte

for single precision and two gigabytes for double

precision. Neither GPU nor Xeon Phi architectures

limit the memory needed by slice-by-slice processing.

A similar workflow for large color image filtering

was proposed in (Nikonorov, Bibikov and Fursov,

2010).

Figure 3: Computation time for different systems.

6 RESULTS AND DISCUSSION

We tested our algorithm on 20 CT images from Sliver

7 database and on 8 of our own CT images and used

proposed metric and visual quality analysis. We also

used 10 CT scans of the abdomen from a publicly

available database (IRCAD) in our evaluation of the

proposed one-point CNR measure (10).

The implementations of bilateral filter and

curvature anisotropic diffusion filter can be found in

ITK library (Johnson et al., 2013). The following

parameters were used for bilateral filter: domain

sigma of 7, range sigma of 7; and for curvature

anisotropic diffusion (Johnson et al., 2013): time step

of 0.09, 8 iterations and a conductance value of 3.0.

The total variance filters have

[0.2,0.4]

∈

We tested different denoising techniques on the

CT images from (IRCAD) database. All images in

this database have a good contrast. However, good

quality venous segmentations are only possible after

a denoising step.

For our evaluation, we used the following

algorithm. We apply different denoising procedures

with TV L1, TV L2 and non-local-means filtering.

Then we compute one-point CNR measure and

perform segmentation. We compared our

segmentation with the ground truth and compute

volume overlap error – VOE (Heimann et al., 2009).

For different CT images the value of one-point

CNR (10) varies, with values typically between 2 and

5. VOE is usually between 5% and 18%. To make

these values comparable across different images, we

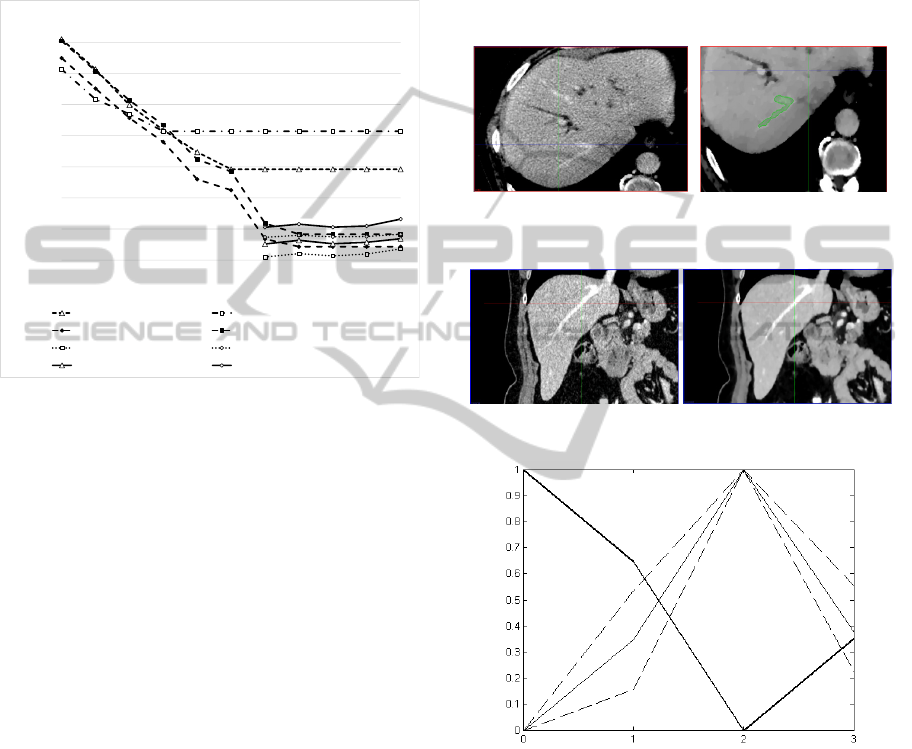
apply normalization to CNR and VOE values. Plots

of normalized VOE and CNR with its 90%

confidence interval values are shown in Fig. 6.

Figure 4: Low quality CT, TV L2 denoising, TV L1

denoising.

Figure 5: High quality CT and its TV L2 denoising.

Figure 6: Normalized VOE (bold), mean normalized value

of measure (10) (regular) and its 90% CI (dashed) for

different denoising parameters applied to 10 CT images.

In Fig. 4 low-contrast CT is shown, the quality

measure (10) for this image is 1.45. The result of TV

L1 denoising has the quality measure of 3.24, for TV

L2 denoising – 2.83. As shown in Fig. 4, the visual

quality for TV L1 is also better. This denoised image

allows us to segment a portion of the hepatic vein

(central-bottom part of the Fig. 4). This branch of

hepatic vein could not be separated otherwise. Only

TV L1 filtering made it possible to perform a

complete segmentation of hepatic veins in this CT

128

256

512

1024

2048

4096

8192

1 2 4 7 16 23 128 236 256 512 1024

Calculation time, milliseconds

Number of threads

Calculation time on different devices

Xeon E5-2695 v2, SP & DP i7 4770K, SP & DP

Xeon Phi 5110P, SP Xeon Phi 5110P, DP

Tesla K20m, SP Tesla K20m, DP

GTX770, SP GTX770, DP

Contrast-to-NoisebasedMetricofDenoisingAlgorithmsforLiverVeinSegmentation

data using previously described segmentation

technique.

A low-contrast example is compared to a high-

contrast one shown in Fig. 5. Quality measure for this

image is 2.81, the quality increased to 8.62 after

denoising.

Quality measure values for bilateral filtering and

curvature diffusion are lower than results obtained

with non-local-means filter and total variance

denoising. Sample results obtained on two low-

contrast CT images (with a quality lower than 2) and

on two CT images with normal contrast are shown in

table 1.

Table 1: Image quality measure for denoising.

Image type

Image number/Quality measure (10)

Image

#21

Image

#22

Noisy image 1.45 1.86 2.81 2.27

Bilateral

filtering

2.11 2.13 5.83 3.12

Curvature

diffusion

1.87 2.45 6.17 2.87

Non-local-

means

2.30 2.67 8.89 4.13

TV L2 2.83 2.44 8.62 3.78

TV L1 3.23 2.94 8.17 3.65

These results allow us to make the following

conclusions. First, proposed one-point contrast-to-

noise based CT image quality measure helps to

predict the quality of the segmentation and allows

detection of the low-contrast CT data. It is also a

useful in choosing the best denoising procedure and

its parameters for individual CT scans.

Second, for CT images with good contrast and a

quality measure higher than 2.0, results for total

variance algorithm using

and

norms and non-

local-means are close. Non-local-means produce a

slightly better denoising results, which is similar to

the findings in (Buades, Coll and Morel, 2006).

Third, TV

denoising shows significantly

better results for low-contrast images. While these

low quality images represent only 20% of our data

set, only TV

filtering makes whole venous

segmentation technique from section 4 possible.

As shown in section 5, HPC implementation

reduces the time of the TV

denoising procedure

while maintains its effectiveness. It makes this

denoising method the best practical choice for

preprocessing low-contrast CT data with quality

measure (10) lower than 2.0.

The results achieved with an HPC-based

implementation of TV L1 algorithm opens new

opportunities in exploring computationally intensive

hepatic segmentation algorithms, as well as other

aspects of image-guided surgery such as non-rigid

registration and real-time tracking. This will be

explored in subsequent research.

Improvement to the segmentation technique for

low contrast images is another interesting area to

explore. The challenge here is that the image requires

different threshold values in various areas of the CT.

Incorporating threshold prediction in the wave

propagation process during the first step of the

segmentation could be a promising direction. An

HPC implementation of the geodesic active contour

segmentation step could further reduce segmentation

processing time.

REFERENCES

Antiga, L., 2002. Patient-Specific Modeling of Geometry

and Blood Flow in Large Arteries, Ph.D. Thesis.

Basu, S., Das-Gupta A., 1992. The Mean, median and Mode

of Unimodal Distributions: A Characterization, Tech.

report, 21 p.

Brenner, D. J., and Hall, E. J., 2007. Computed

tomography: An increasing source of radiation

exposure. The New England Journal of Medicine, vol.

357, no. 22, pp. 2277–2284.

Buades, A., Coll, B., and Morel, J.M., 2006. A review of

image denoising methods, with a new one. Multiscale

Modeling and Simulation, vol. 4, no. 2, pp. 490-530.

Caselles, V., Kimmel, R., and Sapiro, G., 1997. Geodesic

Active Contours. International Journal on Computer

Vision, vol. 22, no. 1, pp. 61-97.

Chambolle, A., and Pock, T., 2011. A first-order primal-

dual algorithm for convex problems with applications

to imaging. Journal of Mathematical Imaging and

Vision, vol. 40, pp. 120–145.

Heimann, T., et al., 2009. Comparison and Evaluation of

Methods for Liver Segmentation from CT datasets.

IEEE Transactions on Medical Imaging, vol. 28, no. 8,

pp. 1251-1265.

Hendrick, R. E., 2008. Breast MRI. Fundamentals and

Technical Aspects, Springer New York, 254p.

IRCAD, 3DIRCADb team, 3D-IRCADb-01 database,

http://www.ircad.fr/softwares/3Dircadb/ 3Dircadb1/

index.php?lng=en.

Johnson, H. J., et al., 2013. The ITK Software Guide, Third

Edition, 768p.

Li, Z., et al., 2014. Adaptive nonlocal means filtering based

on local noise level for CT denoising. Medical physics,

vol. 41, no. 1, p. 011908.

Magnotta, V. A., and Friedman, L., 2006. Measurement of

Signal-to-Noise and Contrast-to-Noise in the fBIRN

SIGMAP2015-InternationalConferenceonSignalProcessingandMultimediaApplications

Multicenter Imaging Study. Journal of Digital Imaging,

vol. 19, no. 2, pp. 140-147.

Mori, M., et al., 2013. Method of Measuring Contrast-to-

Noise Ratio (CNR) in Nonuniform Image Area in

Digital Radiography. Electronics and Communications

in Japan, vol. 96, no. 7, pp. 32-41.

Nikonorov A., Bibikov S. and Fursov V., 2010. Desktop

supercomputing technology for shadow correction of

color images. Proceedings of the 2010 International

Conference on Signal Processing and Multimedia

Applications (SIGMAP), pp. 124-140.

Nikonorov, A., et al., 2014. Semi-Automatic Liver

Segmentation Using Tv-L1 Denoising and Region

Growing With Constraints. 9th German-Russian

Workshop on Image Understanding, pp. 1-4.

Parikh, N., and Boyd, S., 2013. Proximal Algorithms.

Foundations and Trends in Optimization, vol. 1, no. 3,

pp. 123–231.

Perona, P., and Malik, J., 1990. Scale space and edge

detection using anisotropic diffusion, IEEE

Transactions on Pattern Analysis and Machine

Intelligence, vol. 12, no. 7, pp. 629–639.

Pock, T., et al., 2008. Fast and Exact Solution of Total

Variation Models on the GPU, Computer Vision and

Pattern Recognition Workshops, 2008. CVPRW'08.

IEEE Computer Society Conference on, pp. 1-8.

Rudin, L., Osher, S. J., and Fatemi, E., 1992. Nonlinear total

variation based noise removal algorithms. Physica D:

Nonlinear Phenomena, vol. 60, pp.259-268.

Shang, Q., 2010. Separation and Segmentation Of The

Hepatic Vasculature In CT Images, Nashville,

Tennessee, 113 p.

Shuman, W. P., et al., 2014. Standard and Reduced

Radiation Dose Liver CT Images: Adaptive Statistical

Iterative Reconstruction versus Model-based Iterative

Reconstruction—Comparison of Findings and Image

Quality. Radiology, vol. 273, no. 3, pp. 793-800.

Contrast-to-NoisebasedMetricofDenoisingAlgorithmsforLiverVeinSegmentation