Human-like Humanoid Robot Posture Control

M. Zebenay, V. Lippi and T. Mergener

Neurologische Klinik, Neurozentrum, University of Freiburg, Breisacher Straße 64, Freiburg, Germany

Keywords:

Disturbance Estimation Control, Human-like, Double Inverted Pendulum.

Abstract:

This paper validates experimentally a humanoid posture control concept from neuroscience, called disturbance

estimation and compensation, DEC concept. The DEC control system, different from typical state estimation

systems, is not including a dynamic model of the body. Also, among human posture control models it is

particular in that it uses feedback of multisensory disturbance estimates for compensation, rather than ’raw’

sensory signals. To this end, the system performs fusions of sensory inputs such as vestibular inputs (IMU)

and proprioceptive inputs (joint position and speed). The compensation of external disturbances allows the

control to use low loop gain, with human-like tolerance of time delays and mechanical compliance. This

paper validates the control concept experimentally, measuring the balancing of biped stance of a humanoid 2

DOF robot, Posturob II, while superimposing on support surface tilt either voluntary trunk bending or push

stimuli. The results show that the control concept is robust and able to stabilize the robot’s balance in complex

disturbance conditions. Furthermore, several human-like features such as hip-ankle coordination emerged

from the control concept.

1 INTRODUCTION

Humanoid robots require bipedal balancing in many

tasks such as walking, which is different from tradi-

tional industrial robots that are ﬁxed to the support,

not requiring mobility to perform their tasks. Cur-

rently, humans are still superior to robots with re-

gard to robustness and versatility in the control of

bipedal balancing (Nori et al., 2014). Human-likeness

of bipedal control is nowadays an important research

topic (Torricelli et al., 2014). Humanoid balancing

is often based on the zero moment point control or

related measures, which try to keep the center of

pressure within the base of support under the feet

(Goswami, 1999). For this purpose, robots are of-

ten equipped with torque sensors or contact force sen-

sors to control such quantities directly (Cheng et al.,

2007). However, some kind of inertial measuring unit

(IMU) system is required to allow the robot to bal-

ance without making assumptions about the support

surface. In this paper, the compensation of external

disturbances is based on the control of joint torques

using a human inspired vestibular system (Mergner

et al., 2009) that senses the position of the robot in

space and integrates it with signals from other sensors

such as joint angle encoders.

The model used in this work is the DEC (distur-

bance estimation and compensation) model (Mergner,

2010). It is based on studies of human posture control

and movement perception. Postural control allows

humans to make their voluntary movements smooth

and skillful. Postural adjustments provide the move-

ment buttress that the action-reaction law of physics

prescribes and maintain body equilibrium by balanc-

ing the body’s center of mass (body COM) over the

base of support. Impairment of posture control in hu-

mans tends to produce severely disabling syndromes

such as ataxia caused by damage of the cerebellum

or sensory systems, with jerky and dysmetric move-

ments and postural instability (Bastian, 1997).

Various models of human posture control have

been proposed. These posture control models differ

in the approach to internally reconstruct the external

disturbances. One is a control engineering approach

that relates known postural response criteria to exter-

nal disturbances using internal model-based methods

(van der Kooij et al., 1999; Kuo, 2005). The other

approach is mainly biologically inspired, trying to re-

produce human response data in model simulations.

In a reductionist approach, the Independent Channel,

IC model (Peterka, 2002) describes human reactive

sway behavior as the result of three sensory feed-

304

Zebenay M., Lippi V. and Mergener T..

Human-like Humanoid Robot Posture Control.

DOI: 10.5220/0005542603040309

In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 304-309

ISBN: 978-989-758-123-6

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

back loops (vestibular, joint angle proprioception, vi-

sion). Changes in disturbance magnitude and modal-

ity as well as sensor availability are accounted for

by the experimenter using sensory re-weighting rules.

The here considered DEC model uses sensor fusion-

derived internal reconstructions of the external distur-

bances having impact on body posture. The sensory

re-weightings in the DEC model occur automatically

through inter-sensory interactions and non-linear pro-

cessing in the estimators.

Both the IC and the DEC model originally were

restricted to human balancing responses to moder-

ate disturbances in the sagittal plane around an axis

through the ankle joints. This allowed simplifying

the body biomechanics as a single inverted pendulum,

SIP. In this form, the DEC model was re-embodied

into a SIP postural control robot (Mergner et al.,

2006). The robot was successfully tested in the hu-

man test bed (Mergner et al., 2009), reproducing the

human responses to external stimuli in various dis-

turbance scenarios and changes in sensor availability

(Maurer et al., 2006; Schweigart and Mergner, 2008;

Mergner et al., 2003; Cnyrim et al., 2009; Mergner

et al., 2009). Further development of the DEC model

included its preliminary extension to double inverted

pendulum (DIP) biomechanics, adding hip joints to

the ankle joints. This allowed investigating the hu-

man control underlying the coordination between hip

and ankle joint using a hip joint control and an ankle

joint control interconnected by sensory signals (Het-

tich et al., 2014). Furthermore, the DEC control also

was generalized for multiple DOFs and tested in sim-

ulations (Lippi et al., 2013). In this paper, the control

system is further validated using the Posturob II plat-

form by superimposing two external disturbances as

well as an external disturbance with a voluntary lean.

In the following, Section 2 presents the general

concept of the DEC model. Section 3 describes the

experimental setup. The results are presented in Sec-

tion 4. Finally, conclusions are made and outlooks

into the future are given in Section 5.

2 DISTURBANCE ESTIMATION

The DEC model is based on inter-sensory interactions

(Mergner, 2010). It evolved from neuroscience re-

search on human perception of self-motion and biped

balancing to external disturbances. The concept was

developed in an iterative process using balancing ex-

periments and model simulations. The concept uses

estimates of external stimuli that provide the feedback

to the controller.

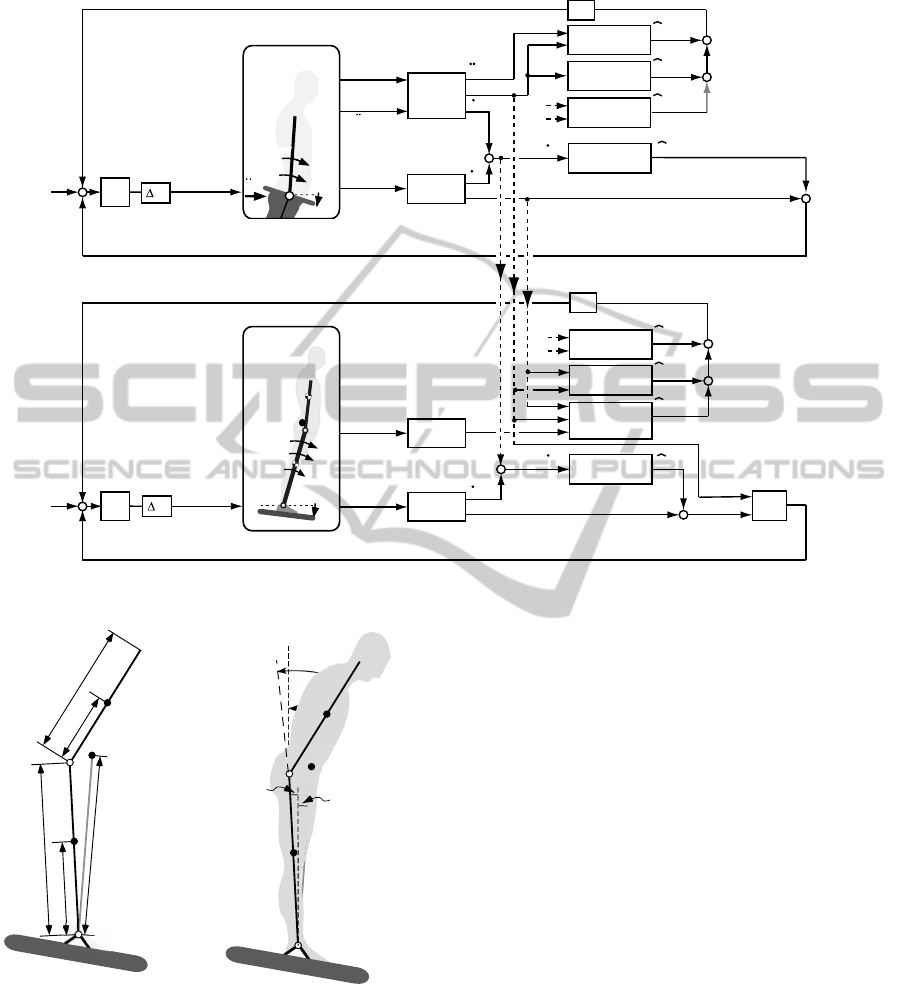
Figure 1 gives an overview of the DEC controller

with a control module for whole body COM balanc-

ing in the ankle joints of the robot and a second DEC

module to control trunk-space (TS) orientation in the

hip joints. Each module contains in its lower part a

control loop for negative feedback, which in humans

together with passive joint stiffness and damping from

muscular-skeletal tissue yields a servo control (not

shown in Fig. 1). With appropriate parameter adjust-

ments of the servo, the actual movement corresponds

to the desired movement deﬁned by a set point sig-

nal (voluntary pose or displacement trajectory). This

applies only in the absence of external disturbances.

External disturbances need to be estimated and com-

pensated, which is done on the basis of sensory inputs.

The external disturbances having impact on the

robot during balancing can be assigned to one of four

classes: (1) Support surface tilt, (2) support surface

translation, (3) contact forces such as a push against

or pull on the body, and (4) ﬁeld forces such as grav-

ity. The sensor inputs in the here considered exper-

imental condition (eyes closed standing balance) are

(a) proprioceptive sensation of the ankle joint angle

and (b) angular velocity, (c) proprioceptive sensation

of ankle torque, (d) a vestibular sensation of the head

in space orientation with respect to the gravitational

vertical (space vertical, SV), (e) head rotation veloc-

ity, and (f) head translational acceleration. The dis-

turbance estimations are derived from these sensory

inputs through sensor fusions and comprise in addi-

tion a detection threshold and a gain factor.

Figure 2 gives the conventions of the DIP used for

the model. Note that physical variables are presented

in upper case letters and their sensor-derived inter-

nal representations in the model as lower case letters.

Signal fusions follow a summation semantics: trunk-

space angle results from combining additively head-

space and trunk-head angles, α

= α

+ α

(invalid

combinations would be α

− α

or α

+ α

). This

applies for the disturbances estimations as well as for

the sensory couplings between the hip with the ankle

control module. Note the simpliﬁed notation of an-

gles and angular velocity in the model of Fig. 1 as

compared to Fig. 2.

The disturbance estimates command the servo to

compensate the disturbances. This addition of a loop

overall increases the loop gain, which generally tends

to be slightly above the minimum for balancing. The

increase occurs only during and to the extent of the

external disturbance. The four estimation and com-

pensation loops are taken to represent in humans long

latency pathways via higher brain centers (basal gan-

glia, cerebral cortex). In Fig.1, the three upper dis-

turbance estimators in the modules are viewed as pro-

ducing torque signals. For feedback, these signals are

Human-likeHumanoidRobotPostureControl

305

HH__ggrraavv

H_in

A_grav

Ankle Module

External Hip

Torque

Gravitational

Hip Torque

Translational

Acceleration

Leg - Space

Tilt

H_ext

H_grav

H_in

Head

TS!

(

T )

Gravitational

Ankle Torque

Translational

Acceleration

Foot - Space

Tilt

A_ext

A_grav

A_in

(T )

COM

ls´´

PROP

VEST

Hip Module

Local Loop Negative Feedback

BS!

= 0°

ts´

External Ankle

Torque

TORQUE

Plant

Trunk-Leg

(TL)

Leg-Foot

(LF)

Trunk-Space

(TS)

Head Acc.

Head

)

Sensors Disturbance estimations

Hip Torque

Ankle Torque

Trunk

Body

A_ext

A_in

COM

Figure 1: Schematics of the DEC model for DIP robot Posture control.

COM

Trunk, T

Legs, L

Figure 2: Conventions of the DIP posture parameters. SV,

space vertical.

transformed into joint angle equivalents (boxes B

and B

). The Local Loops represent short latency

loops through spinal cord and brain stem. Compen-

sation of inter-link coupling forces tend to be covered

by the estimators. Trunk angular acceleration exerts a

coupling force on the leg link, which the ankle control

module treats as a contact force disturbance. Leg an-

gular accelerations produce eccentric rotation of the

hip, which the hip control module treats as distur-

bances in terms of support surface translational ac-

celeration and tilt.

The next subsections present the estimation mod-

els that are used for the DIP humanoid, referring to

conventions deﬁned in Figure 2.

2.1 Estimation of Leg-space Tilt

In the hip module of Fig. 2, the leg-space angle repre-

sents the support surface tilt disturbance for the trunk.

The leg-space angle is estimated using the vestibular

trunk-space angular velocity signal,

and a propri-

oceptive trunk-leg angular velocity signal,

in the

following form:

(

−

)dt (1)

The ﬁnal estimate involves a velocity detection

threshold and a gain factor, both of which were iden-

tiﬁed in human experiments (applies also to following

estimates).

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

306

2.2 Estimation of Foot-space Tilt

In the ankle module, this estimate is obtained from

the vestibular trunk-space angular velocity signal,

(down channeled from leg segment), the propriocep-

tive trunk-leg angular velocity signal,

and the leg-

foot velocity signal,

l f

as follows:

f s



−

l f



dt (2)

2.3 Estimation of Support Translation

The vestibular sensor provides an estimate of trunk

support translation acceleration as follows:

¨x

= ¨x

V x

−

(3)

where ¨x

V x

is a horizontal head (vestibular) transla-

tional acceleration,

is the head angular accel-

eration and l

represents the distance between the

vestibular organ and the hip joint. The ¨x

estimate

is used to estimate the hip torque as follows:

= ¨x

(4)

2.4 Estimation of Gravitational Torque

The estimation of the gravitational ankle torque is

computed as:

grav

= m

gα

(5)

The signal is processed in two parallel pathways, one

via a low pass ﬁlter and gain factor to account for hu-

man data at low tilt frequencies, and the other with

detection threshold and gain factor.

The estimation of the gravitational hip torque is

computed in a corresponding way as:

grav

= m

gα

(6)

2.5 Estimate of Contact Force

An external ankle torque from a push against the body

is computed from a sensory signal of the active ankle

torque ,T

, and an internal estimate of the total torque,

which is obtained from the body-space angular ac-

celeration as follows:

= J

(7)

where the J

is the moment of inertia of the body

around the ankle joint. The external ankle torque is

computed as:

ext

= T

− T

grav

− T

(8)

The external hip torque can be computed in a corre-

sponding way.

2.6 Estimation of Body-space Angle

Compensating in the ankle joint module the body

COM requires its computation (Fig.2, box COM and

inside box Gravitational Ankle Torque). Body-space

position

is computed as:

+ l

+ h

(9)

where m

is body mass, m

is trunk mass, m

is the

mass of both legs, h

is body COM height, h

trunk COM height, h

is leg COM height and l

leg length. Assuming small angular changes, h

is set

constant.

3 EXPERIMENTAL SETUP

PostuRob II (Fig. 3) was constructed with human-

like anthropometric parameters (Hettich et al., 2014).

It consists of trunk, leg and feet segments of alu-

minum, interconnected by hinge joints representing

the hip joints and the ankle joints. Signals from

mechatronic sensors (vestibular, joint torque, joint an-

gular position and velocity) were input into a real time

PC, where the control model was executed as a com-

piled Simulink model (Real-Time Windows Target,

The MathWorks Inc., Natick, USA). The vestibular

Artificial (Pneumatic) Muscles

Vestibular Sensor

Joint Angle Sensors

Joint Torque Sensors

Pressure Sensors

Hip Joints

Ankle Joints

Motion Platform

Figure 3: PostuRob II standing on a motion platform.

sensor processed accelerometer and gyrometer sig-

nals and delivered the signals (i)trunk angular veloc-

ity, (ii)trunk angle with respect to the gravitational

vertical, and (iii)linear acceleration of the upper trunk

end representing the head (Mergner et al., 2009). The

torque commands for hip and ankle joints actuate ar-

tiﬁcial pneumatic muscles (FESTO, Esslingen, Ger-

many). An inner torque control loop ensured that

the actual torque matched the desired torque. Experi-

ments were performed in a human posture control lab-

oratory. External disturbances consisted of support

Human-likeHumanoidRobotPostureControl

307

surface tilt in the sagittal plane while the robot was

standing on a 6 DOF motion platform. Furthermore,

contact force stimuli were applied by pushes with the

hand, and 4

◦

voluntary lean of the trunk was com-

manded via the T S! set point signal (Fig.1) using a

smoothed ramp. Estimated lumped time delays of the

hip and ankle modules were set to 50 ms and 80 ms,

respectively. Together with an estimated time delay

of 40 ms for the PC processing, the delays amounted

to 90 ms for the hip joint control and 120 ms for the

ankle joint control.

4 RESULTS

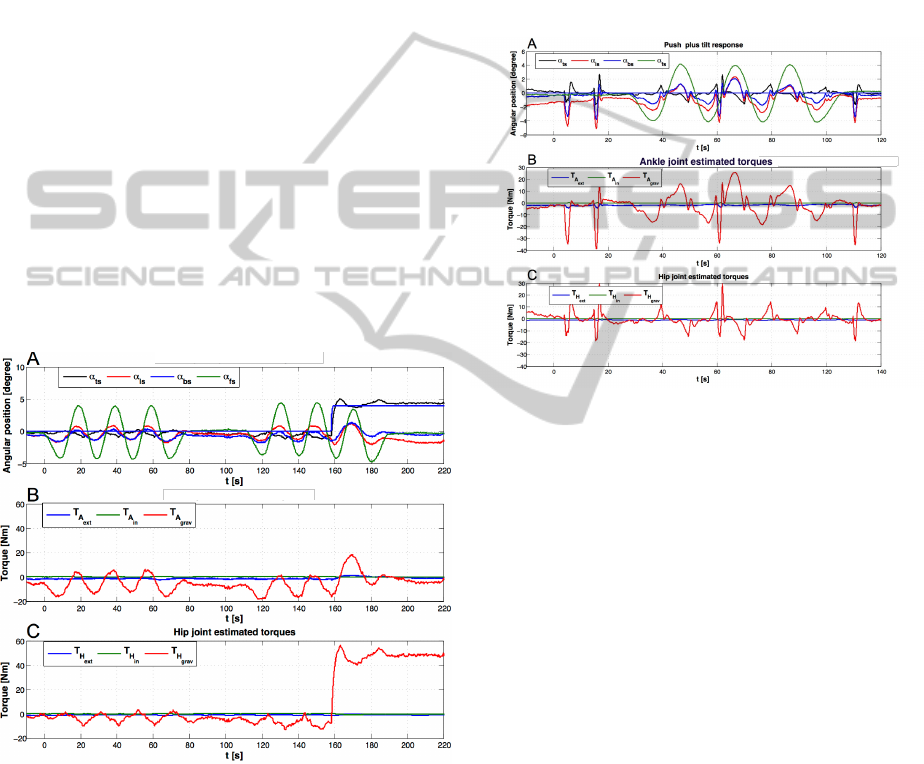
Figure 4 shows in the ﬁrst part the results obtained

with a series of sinusoidal support surface tilts alone.

Panel A gives the evoked kinematic sway responses,

where α

f s

reﬂects essentially the tilt stimulus and α

the body COM balancing response in the ankle joints.

The other two traces are the trunk-space and leg-space

angular excursions. Panels B and C give the sensed

ankle torque and hip torque, respectively. The applied

surface support tilt was of ±4

◦

amplitude and 0.1Hz.

Ankle joint estimated torques

Tilit and Voluntary lean response

Figure 4: Superposition of support surface tilt and voluntary

lean. Kinematic responses (A), sensed torque at the ankle

joint (B) and the hip joint (C).

In the later part of Fig. 4, starting at about 110 s, a

second tilt series starts. At around 160 s, a voluntary

trunk lean of 4 degree forward is superimposed (see

black trace). The DEC module of the hip joint brings

the α

in the desired position, while the DEC module

of the ankle joint continues with the α

balancing.

The forward trunk lean is associated with backward

leg lean in α

(red trace). It is mainly this inter-link

coordination that limits the α

excursion, keeping the

COM above the base of support. This hip-ankle coor-

dination is human-like (Hettich et al., 2014).

Figure 5 shows the results obtained in PostuRob

II when superimposing external push stimuli and sup-

port surface tilt (presentation as in Fig. 4). Four push

stimuli (large transients) were applied, one of them

during a support surface tilt series (sine-like curves).

Thus, the robot’s stance stabilization by the DEC con-

troller tolerates the superposition of the two external

disturbances.

Figure 5: Push responses: A) Angular position responses,

B) and C) are the sensed torques for the ankle and hip, re-

spectively.

5 CONCLUSIONS AND FUTURE

WORK

The experiments show that the DEC controller in

the DIP robot is able to deal with superposition of

more than one type of external disturbances and su-

perposition of external disturbances and voluntary

movements such a trunk lean. The experiments also

demonstrate that the controller is tolerant against

spontaneous body sway originating from internal

noise, mostly from vestibular input, this during the

balancing of external disturbances and in the pres-

ence of a lasting trunk lean that challenged the balanc-

ing. Furthermore, the robot demonstrated a human-

like mechanical compliance, which was particularly

evident in its reactions to the external push.

The experiments also revealed emergence of a hip-

ankle coordination during voluntary trunk lean, which

on closer inspection also occurred in the responses to

external disturbances, and is human-like (Alexandrov

et al., 1998; Freitas et al., 2006). It is related to the an-

kle controller’s task to stabilize the body COM over

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

308

the base of support (it is not found when the task is

to maintain the leg-space orientation vertical). No-

ticeably, the coordination occurs here through the in-

teractions between the hip and ankle control modules

rather than through preprogrammed motor command

patterns, which also have been used to control robots

in the form of synergies (Hauser et al., 2011).

Currently, further developments of the DEC con-

cept comprise tests in different robotics platforms.

Furthermore, under investigation are generalizations

of the modular structure of the DEC controller to

conditions that are not a multiple inverted pendulum.

This includes controlling balance in the frontal plane,

alone and in combination with the sagittal plane bal-

ancing, generic poses with high degrees of freedom,

and integrating the balancing in the control of gait.

In particular, in the framework of the H

R project

(see below), the controller is tested for the balancing

control of a robot with multiple DOFs with compli-

ant actuation, developed within the consortium, and

integrated in the gait controller for the stabilization

of some links. In the framework of the EMBalance

project, the DEC controller is modiﬁed such that the

robot’s balancing behavior mimics certain neurologi-

cal deﬁcits such as bilateral vestibular damage or loss.

ACKNOWLEDGEMENTS

The authors thank G. Hettich and L. Assl

ander

for their support during the experiments. The

ﬁnancial support from the European projects EM-

Bbalance (http://www.embalance.eu/)and H

(http://www.h2rproject.eu/) are appreciated.

REFERENCES

Alexandrov, A., Frolov, A., and Massion, J. (1998). Axial

synergies during human upper trunk bending. Experi-

mental Brain Research, 118(2):210–220.

Bastian, A. J. (1997). Mechanisms of ataxia. Physical Ther-

apy, 77:672–675.

Cheng, G., Hyon, S.-H., Morimoto, J., Ude, A., Hale, J. G.,

Colvin, G., Scroggin, W., and Jacobsen, S. C. (2007).

CB: A humanoid research platform for exploring neu-

roscience. Advanced Robotics, 21:1097–1114.

Cnyrim, C., Mergner, T., and Maurer, C. (2009). Potential

role of force cues in human stance control. Experi-

mental Brain Research, 194:419433.

Freitas, S. M., Duarte, M., and Latash, M. L. (2006). Two

kinematic synergies in voluntary whole-body move-

ments during standing. Journal of Neurophysiology,

95(2):636–645.

Goswami, A. (1999). Postural stability of biped robots and

the foot-rotation indicator (FRI) point. The Interna-

tional Journal of Robotics Research, 18(6):523–533.

Hauser, H., Neumann, G., Ijspeert, A. J., and Maass, W.

(2011). Biologically inspired kinematic synergies en-

able linear balance control of a humanoid robot. Bio-

logical cybernetics, 104(4-5):235–249.

Hettich, G., Asslnder, L., Gollhofer, A., and Mergner, T.

(2014). Human hipankle coordination emerging from

multisensory feedback control. Human Movement

Science, 37:123–146.

Kuo, A. D. (2005). An optimal state estimation model of

sensory integration in human postural balance. Jour-

nal of Neural Engineering, 2(3):S235.

Lippi, V., Mergner, T., and Hettich, G. (2013). A bio-

inspired modular system for humanoid posture con-

trol. . In: Ugur, E., Oztop, E., Morimoto, J., and Ishii,

S. (Eds) Proceedings of IROS 2013 Workshop on Neu-

roscience and Robotics ”Towards a robot-enabled,

neuroscience-guided healthy society”.

Maurer, C., Mergner, T., and Peterka, R. J. (2006). Multi-

sensory control of human upright stance. Experimen-

tal Brain Research, 171:231250.

Mergner, T. (2010). A neurological view on reactive human

stance control. Annual Review Control, 34:77198.

Mergner, T., Huethe, F., Maurer, C., and Ament, C. (2006).

Human equilibrium control principles implemented

into a biped robot. Robot Design, Dynamics, and Con-

trol, 487:271–279.

Mergner, T., Maurer, C., and Peterka, R. J. (2003). A

multisensory posture control model of human upright

stance. Progress in Brain Research, 142:189–201.

Mergner, T., Schweigart, G., and Fennell, L. (2009).

Vestibular humanoid postural control. Journal of

Physiology - Paris, 103:178–194.

Nori, F., Peters, J., Padois, V., Babic, J., Mistry, M., Ivaldi,

S., et al. (2014). Whole-body motion in humans and

humanoids. In Workshop on New Research Frontiers

for Intelligent Autonomous Systems.

Peterka, R. J. (2002). Sensorimotor integration in hu-

man postural control. Journal of Neurophysiology,

88:10971118.

Schweigart, G. and Mergner, T. (2008). Human stance con-

trol beyond steady state response and inverted pen-

dulum simpliﬁcation. Experimental Brain Research,

185:635–653.

Torricelli, D., Mizanoor, R. S., Gonzalez, J., Lippi, V., Het-

tich, G., Asslaender, L., Weckx, M., Vanderborght,

B., Dosen, S., Sartori, M., et al. (2014). Benchmark-

ing human-like posture and locomotion of humanoid

robots: A preliminary scheme. In Biomimetic and Bio-

hybrid Systems, pages 320–331. Springer.

van der Kooij, H., Jacobs, R., Koopman, B., and Grooten-

boer, H. (1999). A multisensory integration model

of human stance control. Biological Cybernetics,

80:299–308.

Human-likeHumanoidRobotPostureControl

309