LLUNPIY Preliminary Extension for Simulating Primary Lahars

Application to the 1877 Cataclysmic Event of Cotopaxi Volcano

Guillermo Machado

1,3

, Valeria Lupiano

, Gino M. Crisci

and Salvatore Di Gregorio

Dept. of Mathematics and Computer Science, University of Calabria, Arcavacata, 87036 Rende, Italy

Dept. of Biology, Ecology, Earth Science, University of Calabria, Arcavacata, 87036 Rende, Italy

Faculty of Engineering, National University of Chimborazo, 060150 Riobamba, Ecuador

Keywords: Modelling, Simulation, Cellular Automata, Lahars, Cotopaxi, Natural Hazard, LLUNPIY.

Abstract: Cotopaxi volcano is one of the most studied and surveyed volcanos in the world because the repetition of

the 1877 catastrophic lahar invasion, is not implausible, threatening now more than 100,000 persons. A

reliable forecasting tool is very important for projecting security measures. LLUNPIY is a Cellular

Automata model for simulating lahars in terms of complex system evolving on the base of local interaction.

Here, LLUNPIY extension is applied to Cotopaxi event of 1877 primary lahars, after the successful

simulation of some secondary lahars of Tungurahua volcano. Such an extension permitted simulations with

different initial hypotheses: our preliminary simulations agree in outline with field studies about the

evolution of event, moreover LLUNPIY permits a broader approach to overall phenomenon in comparison

with other tools.

1 INTRODUCTION

Volcanic eruptions can generate directly (primary

lahars) or indirectly (secondary lahars) catastrophic

surface flows that are a mixture of volcanic debris

and water occurring on and around volcanoes

(Vallance, 2000), other than normal streamflow

(Smith and Fritz, 1989), with consistency, viscosity

and approximate density of concrete: they are fluid,

when sloping moving up to 100 km/h as far as

extreme distance of 300 Km, solid at rest in the flat

terminal zone (Hoblitt et al., 1987). They may be

primary lahars, for instance, when lava or

pyroclastic flows melt snow and glacier and/or mix

with wet soil generating a flood sometime also with

the water of broken basin (Manville et al., 2013;

Pistolesi et al., 2014). Typical instances are the

1949, 1963 e 1971 lahars at Villarica, Chile

(Vallance, 2005), when lava flows melted snow and

glacier and broke a pond. Secondary lahars instead

occur from the post-eruptive when heavy rainfalls,

typhoons or lake breakout mobilize ash and other

volcanic debris of previous volcanic activities (e.g.

2005, 2008 lahars of Tungurahua volcano simulated

by Partial Differential Equations (PDE) and Cellular

Automata (CA) methods (Williams et al., 2008;

Machado., et al. 2014).

Lahars are very complex dynamical systems,

very difficult to be modelled: they can grow by soil

erosion and/or incorporation of water, along

watercourses. Unconsolidated pyroclastic material,

(Major et al., 2000; Manville et al., 2000), can be

easily eroded by superficial water forming dilute

sediment-laden flows, that can bulk-up to debris

flows whose magnitude will depend upon the

volume of both the water and remobilized material

(Barclay et al., 2007).

A variety of approaches have been taken to

model the behaviour of lahars and the hazards posed

to downstream communities (Manville et al., 2013):

empirical models based on smart correlations of

phenomenon observables (Schilling, 1998; Muñoz-

Salinas et al., 2009), simple rheological and

hydrological models, which assume acceptable

simplifications as composition-independent flow

behaviour or Newtonian flow behaviour (Costa,

2004; O’Brien et al., 1993), PDE approximating

numerical methods of complex physical behaviour

of lahar (Pitman et al., 2003).

CA represent an alternative methodological

approach for modelling and simulating complex

systems evolving on the base of local interactions.

Intuitively, a CA can be seen as a space, partitioned

in regular cells, each one embedding an identical

367

Machado G., Lupiano V., Crisci G. and Di Gregorio S..

LLUNPIY Preliminary Extension for Simulating Primary Lahars - Application to the 1877 Cataclysmic Event of Cotopaxi Volcano.

DOI: 10.5220/0005542903670376

In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),

pages 367-376

ISBN: 978-989-758-120-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

input/output computing unit. Each cell is

characterized by its state. S is the finite set of the

states. Input for each cell is local and is given by the

states of m neighbouring cells, where the

neighbourhood conditions are given by a pattern

invariant in time and space. At time 0, cells are in

arbitrary states (initial conditions) and the CA

evolves changing simultaneously the state at discrete

times, according to (local, depending on the input)

rules, that are invariant in time and space.

Surface flows are a typical application of

Multicomponent (or Macroscopic) Cellular

Automata (Di Gregorio and Serra, 1999; Avolio et

al., 2003) for computer simulation: SCIARA model

for lava flows (Avolio et al., 2006), SCIDDICA

(Avolio et al., 2010) for debris flows, PYR (Crisci et

al., 2005) for pyroclastic flows, VALANCA (Avolio

et al., 2010) for snow avalanches, SCAVATU

(D’Ambrosio et al., 2001) for soil erosion by

rainfall.

A very important characteristic of all these

models is that they are based on two dimensions CA,

but they work effectively in three dimensions

because the third dimension is enclosed in part of the

sub-states: altitude, kinetic head, lahar thickness,

depth of erodible pyroclastic stratum, and so on.

We developed LLUNPIY in a first version for

simulating secondary lahars with applications to

2005 and 2008 Tungurahua lahars. An extension

was performed in order to capture the behaviour of

primary lahars and two different applications related

to initial phase were accomplished for 1877

Cotopaxi catastrophic lahars.

The second section of the paper describes the

geological features of the phenomenon related to

Cotopaxi volcano characteristics. The third section is

devoted to the LLUNPIY model applied to the

simulations that are presented in the fourth section.

At the end comments and conclusions.

2 COTOPAXI VOLCANO

Cotopaxi volcano is situated in the Eastern

Cordillera of the Ecuadorian Andes (Figure 1) about

60 km south of Quito, and it is a very hazardous

active stratovolcano.

With an altitude of 5897 m a.s.l. the summit of

the volcano is currently covered with a thick layer of

ice that ranges between 30 and 120 m (Cáceres et

al., 2004). Cáceres et al. (2004) estimated that the

glacier volume was approximately 1,000 million m

in 1976, considering an average thickness of 50 m.

Such a volume has been reduced to 732 million m

in 1997, because of a progressive melting, probably

generated by climate change.

The main drainage lines are: in north sector there

is the Pita-Guayallabamba River, the west slopes are

crossed by several tributaries of the Napo River,

while waters of several streams, often encased in

narrow valleys, coming from the cone of volcano,

converge into the Rìo Cutuchi, that flows toward

south-southwest in the wide valley of Latacunga.

Figure 1: Cotopaxi volcano and its surrounding region.

The area around the volcano is densely populated, in

fact, the city of Quito is located in north. In the

Cutuchi valley besides several villages, there are the

towns of Latacunga and Salcedo, respectively 45 km

and 50 km in south of Cotopaxi. In addition,

industries and agriculture are intensively developed

in these areas.

Since 1738 Cotopaxi has erupted more than 50

times. The most violent historical eruptions were in

1744, 1768, 1877, and 1904 with generation of

disastrous lahars in many cases.

2.1 1877 Lahars

The presence of glacier on summit of Cotopaxi is

one of principal causes, together with volcanic

eruptions (lava or pyroclastic flows), of primary

lahars. In fact, the Cotopaxi has often produced

catastrophic lahars during eruptions because of ice

and snow melting.

The 1877 eruption, described by Sodiro (1877)

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

368

and Wolf (1878), produced very destructive and

large lahars. These chronicles report times and

extension of lahar floods next to inhabitant centres:

some later observations estimated the glacier

melting to 1/10 of total volume (Wolf, 1878). Water,

which originates from melting glacier, had been

mixed with pyroclastic material erupted and with

pre-existing volcanoclastic materials outcropping

along slopes, so many lahars flows had been

generated (Figure 2). These flows, channelled in

drainage network, destroyed population centres and

everything on the path.

On the western slope of volcano, three main

flows are generated, coming down with a

conjectured speed from about 30 m/s to about 10 m/s

(depending on the slope) and reaching Latacunga, a

village, at that time, in about one hour (Mothes et

al., 2014).

Figure 2: Reconstruction of 1877 lahar path (from Mothes

et al., 2014).

3 LLUNPY MODEL

In this section, we present an extension of

LLUNPIY model with the purpose of capturing the

dynamical behaviour of primary lahars in the

southern drainage system of the Cotopaxi volcano.

LLUNPIY (Lahar modelling by Local rules based

on an UNderlying PIck of Yoked processes) derives

from the Quechua word llunp’iy, that means flood.

The first version has been developed to simulate

secondary lahars with applications to two events at

Tungurahua volcano (Machado et al., 2014 and

2015).

Lahars triggered by mobilization of deposits

from volcanic explosions have occurred at Cotopaxi

volcano, Ecuador on the average of once every

century over the last two millennia. Lahars from

Cotopaxi are possible to flow down along three main

drainages, affecting a present day population of

around 100,000 inhabitants.

Primary lahars were modelled using LLUNPIY

in three main stages. Generation stage: lahars are

generated from pyroclastic flows and melting of the

volcano’s icecap, due to interaction of eruptive

products with a summit glacier. This stage, the

glacier melting, is an extension of the previous

version of LLUNPIY, that models raining, water

flows and percolation in the soil and successive

mobilization of pyroclastic stratum; the raining

contribute is zero for the Cotopaxi event. Flood

stage: lahar flows develop along the volcano steep

slopes with high gravitational potential energy and

turbulence with possible soil erosion and water

inclusion along watercourses. Final stage: the lahar

flow reduces its kinetic energy and velocity in flat

areas; rapid decrease of turbulence causes deposit

and solidification processes by water extrusion; in

some cases, lahar can partially “be diluted” and

“disappear”, if it runs into a watercourse with a

water flow, enough large to englobe the lahar matter.

3.1 Formal Definition of LLUNPIY

The extension of LLUNPIY model is a two

dimensional CA with hexagonal tessellation and

defined by the septuplet:

<R, G, X, S, P,, >

(1)

 R = {(x, y)| x,y , 0 ≤ x≤ l

, 0 ≤ y ≤ l

} is

the set of points with integer co-ordinates, that

individuate the regular hexagonal cells,

covering the finite region, where the

phenomenon evolves.  is the set of natural

numbers;

 G  R is the set of cells, corresponding to the

glacier, where lahar is formed when

pyroclastic matter melts ice;

 X = {(0, 0), (1, 0), (0, 1), (−1, 1), (−1, 0),

(0,−1), (−1,−1)}, the neighbourhood index,

identifies the geometrical pattern of cells,

which influence state change of the “central”

cell (Figure 3): the central cell (index 0) itself

and the six adjacent cells (indexes 1,..,6);

 S is the finite set of states of the finite

automaton, embedded in the cell; it is equal to

the Cartesian product of the sets of the

considered sub-states (Table 1).

 P is the set of the global physical and

LLUNPIYPreliminaryExtensionforSimulatingPrimaryLahars-Applicationtothe1877CataclysmicEventofCotopaxi

Volcano

369

empirical parameters, which account for the

general frame of the model and the physical

characteristics of the phenomenon (Table 2);

 : S

S is the cell deterministic state

transition in R, it accounts for the following

main components of the phenomenon: lahar

flow, soil mobilization and erosion. Water

inclusion and extrusion, lahar solidification

are not considered for Cotopaxi case, because

such primary lahars followed the river paths

and largely overflowed, they lost in the ocean

during the final phase;

 :

G S expresses the “external influence”

of fall of the pyroclastic matter on glacier and

consequently ice state change in lahar with the

addition of pyroclastic matter for G cells at the

initial CA steps.  is here referred to the step

number.

Table 1: Sub-states regarding the generation phases.

SUB-STATES DESCRIPTION

, S

cell Altitude, Ice Thickness,

, S

LWC

Lahar Thickness, Lahar

Kinetic Head, Lahar Water

Content

, S

the co-ordinates X and Y of

the lahar barycenter inside the

cell

, S

KHE

(6 components)

External flow normalized to a

thickness, External flow co-

ordinates X and Y, Kinetic

Head of External flow

, S

. S

, S

KHI

(6 components)

Internal flow normalized to a

thickness, Internal flow co-

ordinates X and Y, Kinetic

Head of Internal flow

3.2 Generalities of  and 

In the formulae, a sub-state is specified by S, its

right subscript is a shortening of the sub-state name

in capital letters (e.g., S

, the sub-state altitude); if

the left subscript is not specified, the sub-state is

related to the central cell of the neighbouring; when

other cells of the neighbouring must be considered,

the left subscript specifies the index of the

neighbouring cell, e.g.,

, is the sub-state altitude

of the cell with index 1 in the neighbouring. Sum of

indexes of opposite cells is always 7 as in Figure 3.

’ indicates the updated value of the generic

sub-state S

. S

means S

value variation.

Quantities related to volumes as outflows are

normalized to lengths, because the cell area is

Figure 3: Geometrical pattern of cells.

Table 2: Physical and empirical parameters.

AMETERS DESCRIPTION

, p

cell apothem (m), temporal

correspondence of a CA step

(s)

friction coefficient parameter

(°)

, p

lahar parameters: turbulence

dissipation (-) and erosion

dissipation (-) of energy;

lahar parameter of

progressive erosion (-),

mobilization threshold (m)

slt

slope threshold (°)

khl

kinetic head loss (m)

constant in value.

The lahar inside a cell is modelled as a

“cylinder” tangent the next edge of the hexagonal

cell with mass, velocity and barycentre co-ordinates.

Movements of cylinders from central cell toward

adjacent cells originate: internal flows (cylinder shift

is all inside the cell), external flows (cylinder shift is

all outside the cell) and mixed situations.

Computations of lahar flows are based on the

Algorithm of the Minimization of Differences

(AMD) for determination of minimizing outflows f

1i6, (i.e., the flows that minimize differences in

height for the cell neighbourhood) and the

determination of outflow shifts (Di Gregorio and

Serra, 1999; Avolio et al., 2012). AMD involves

different specification of “heights” h

, the “fixed”

parts and d, the “distributable” part. Motion

equations specify a shift x and a final velocity v, in

order to determine from initial f

(1i6) the

outflows f

’ (0i6) during a step. Lahar kinetic head

is obtained by:













2

(2)

where  is the gravity acceleration, the subscripts l

means lahar.

The application of  function is here simplified:











and 





0 in the first step.

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

370

3.3 Specification of 

The main “elementary processes” of LLUNPIY are

outlined in the following.

3.3.1 Lahar Thickness and Outflows

Lahar in the cell and its lahar outflows are computed

in similar way as debris in the cell and its debris

flow in SCIDDICA-SS2 and improvements (Avolio

et al., 2008; 2009; Lupiano et al., 2014a; 2014b).

SCIDDICA means Simulation through

Computational Innovative methods for the Detection

of Debris flow path using Interactive Cellular

Automata, while SS2 means second version for both

Subaerial and/or Subaqueous debris flow simulation.

The outflow path from the central cell to a

neighbouring cell i follows an ideal direction

between two points: the lahar barycentre of central

cell and the centre of the adjacent cell i accounting

for slope θ

(Figure 3).

Viscosity is modelled as the part of lahar

thickness, that cannot be movable (Avolio et al.,

2006) according to a function that computes an

“adherence” value between two values p

adh1

and

adh2

in linear way.

Viscosity represents “de facto” the lahar deposit

along the path at the phenomenon ending except the

solidification deposit.

In the case of this primary lahar, adherence is a

constant value p

adh

in order to account the

catastrophic features of the phenomenon with an

enormous quantity of melted water, plus the river

water, so that the lahar keeps extremely fluid.

AMD is so applied:

 











(3)

























(4)





















(5)

The motion equations are related to outflows from

central cell toward the adjacent cell i (1i6):













sin







∙cos











(6)

















∙







 (7)

where v

is the initial velocity (deduced by S

), x

the shift of the outflow toward the cell i,



is the

slope angle between the central cell and the

neighbour i;

Sub-states regarding outflows are computed in

the same way as debris flows in SCIDDICA-SS2

(Avolio et al. 2008).







, 





, 





, 





are computed by balancing

equations that consider the contribute of outflows

and inflows:















 























(8)

where 











is the outflow of neighbouring cell i

toward the cell 0, that is specified by component 7-i

for the neighbouring of cell i. An average weight is

also considered:































(9)



∑



































































∑

































(10)



∑











































































∑

































(11)



∑



















































A turbulence effect is modelled by a proportional

kinetic head loss at each LLUNPIY step: ∆













. The turbulence affects kinetic head and

consequently the velocity. This formula involves

that a velocity limit is asymptotically imposed “de

facto” for any value of slope.

3.3.2 Soil Erosion

When the kinetic head value overcomes an

opportune threshold (







) depending on the

soil features then a mobilization of the pyroclastic

cover occurs proportionally to the quantity

overcoming the threshold:

















∆



(12)

because the pyroclastic cover depth diminishes as

the debris thickness increases); the kinetic head loss

is:

∆



















(13)

The mixing of the eroded pyroclastic cover with the

earlier debris involves that the earlier debris kinetic

energy becomes the kinetic energy of all the mass of

LLUNPIYPreliminaryExtensionforSimulatingPrimaryLahars-Applicationtothe1877CataclysmicEventofCotopaxi

Volcano

371

debris, it implicates trivially a further kinetic head

reduction:















∆









∆



(14)

4 SIMULATIONS OF 1877 EVENT

Necessary input data for simulation of primary

lahars with LLUNPIY are:

 DEM (Digital Elevation Model) with adequate

cell-size;

 Source areas: extension of glaciers, whose

melting originates lahars, or extension of

ponds/lakes, whose destruction by volcanic

matter releases enough water to generate

lahars;

 Specifications of volcanic activity (eruption

duration, strength and range of action) that

effects glacier melting and/or destruction of

ponds/lakes;

 Detachment areas: this is an alternative to

simulate volcanic activity, the phenomenon

starts in the areas immediately out of the

volcanic action range by specifications of

“initial” quantities of lahar;

 Erodible pyroclastic cover.

In order to calibrate model parameters it is

fundamental to identify the lahar path and invaded

area of real phenomenon in order to measure the

simulation “goodness”.

We referred for 1877 event simulation to the

2010 DEM with 30m cell size with vertical accuracy

from 0.6 m to 1.3 m (supplied to us by Instituto

Geofísico of the Escuela Politécnica Nacional -

IGEPN), that is a very large size but considering the

magnitude and extent of the phenomenon was

considered acceptable, if changes in the time are also

considered. Erodible detrital cover was considered a

uniform layer of 5 m thick because field data are not

available in all the simulation area.

4.1 “Many Sources” Simulations

We considered, as first approach, the hypothesis

(Mothes et al., 2014; Pistolesi et al., 2014) that the

main event could be equivalently generated

considering the initial positions of lahars sources in

the three principal streams (Figure 4b): Río Cutuchi,

Río Sasqìmala and Río Barrancas-Alaques.

Only the lahars flowing in the Cutuchi valley

were considered, taking into account that the flows

toward south may be considered independent from

the other ones in the real phenomenon.

In each of these three streams we have placed,

respectively, 18.5 10



, 9.510



and

1010



of lahar matter.

The resultant simulations are shown in figure 4a.

The flows along Río Cutuchi and Río Sasqímala

converge together at elevation of 3000 m a.s.l. after

60 minutes of triggering, while the lahar, that flows

in Río Barrancas-Alaques, joins the main stream

further south in 68 minutes. The simulated lahar

flows reached Latacunga in one hour and 30 minutes

at average velocity of 8 m/s.

These results are comparable with simulations

performed by the model LAHARZ (Pistolesi et al.,

2014), that considered larger quantities of initial

lahars (120 10



sum of: 60 10



Río Cutuchi, 3010



in Río Sasqímala and

3010



in Río Barrancas-Alaques).

Positioning lahar sources in the top of Río Cutuchi,

Figure 4: a) LUNPIY simulation of 1877 lahars; b)

position of considered lahars sources (blue point).

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

372

Río Sasqímala and Río Barrancas-Alaques involves

a limit for LLUNPIY because quantity that exceeds

greatly the bed of rivers can follow other paths; this

may be not justified. Furthermore, LAHARZ does

not model soil erosion, which increases lahar flows.

LLUNPIY models the erosion that increases the

lahar initial quantity. If we compare the

reconstruction of the real event, made by Mothes et

al. (2014) by field data, the width of LLUNPIY

simulation is smaller in the area around the vent, but

LAHARZ simulation is larger (Figure 5). In the

following phases, the two simulations become

always closer. The two results are very similar in the

final sector (Latacunga area), because, at the end, the

addition of eroded material balances the two

approaches. We remember that LAHARZ

simulations consider only the lahar extension, but

not times and velocity. A further comparison could

be possible, considering the glacier melting for

LLUNPIY in order to simulate lahars since their

very first origin. The next section reports such a case

with the worst hypothesis of total icecap melting.

4.2 “Glacier Melting” Simulation

The previous approach with CA involves the limit of

initial quantity of lahar at the sources, because

overflows can distort the effective evolution of the

phenomenon. This did not permit to overcome an

initial lahar quantity at the beginning in the previous

simulation. For this purpose, we introduce the CA

“elementary process” of melting glacier by

pyroclastic flows or bombs. The ice layer is

supposed to enclose pyroclastic matter and to melt

immediately (the LLUNPIY first step) the glacier;

that is more realistic than sources approach, if the

rapid evolution of eruption is considered. The

simulations of icecap melting are based on data,

which correspond to 1976 glacier extension with

average glacier thickness of 50 m (Cáceres et al.,

2004). Simulation initial conditions account only for

that part of glacier that is able to feed lahars towards

Cutuchi valley (sectors 11-19 in figure 6g).

The evolution of other flows represents partial

results only in the first steps of simulation.

In the simulation (Figure 6

a, b, c, d, e, f), lahars

reach a maximum height of 50 m in Río Cutuchi and

Río Barrancas-Alaques; since the icecap initial

melting, the flows join in Cutuchi valley from main

drainage lines after 50-60 minutes and reach the

town of Latacunga after 1 hour and 35 minutes; that

is 35 minutes late in comparison with times, that are

reported in the chronicles. These results are

comparable with simulations performed by the

model LAHARZ, that considered initial larger

quantities of lahars in the case of “many sources”

simulation, while the worst case of “icecap melting”

generated a larger quantity of lahar toward the

Cutuchi Valley. The paths are the same, but widths

are obviously larger.

Figure 5: Comparison among LLUNPIY simulation,

LAHARZ simulation and partial reconstruction of real

event.

5 CONCLUSIONS

We applied LLUNPIY, a CA model, in order to

attempt simulations of 1877 primary lahars occurred

in Cutuchi Valley, south west sector of Cotopaxi

volcano. A careful analysis was performed in order

to obtain the most faithful reconstruction of such a

catastrophic event.

Simulations were performed by desktop pc with

Processor Intel(R) core i7, CPU 2.8GHz and

NVIDIA Quadro FX 580 video card. The CA is

1154x1733 cells large.

The adopted programming language is C++, the

model is implemented in a “skeleton” fashion,

developed for MCA, where the transition function is

divided into the “elementary processes” of

LLUNPIY. Such elementary processes are executed

LLUNPIYPreliminaryExtensionforSimulatingPrimaryLahars-Applicationtothe1877CataclysmicEventofCotopaxi

Volcano

373

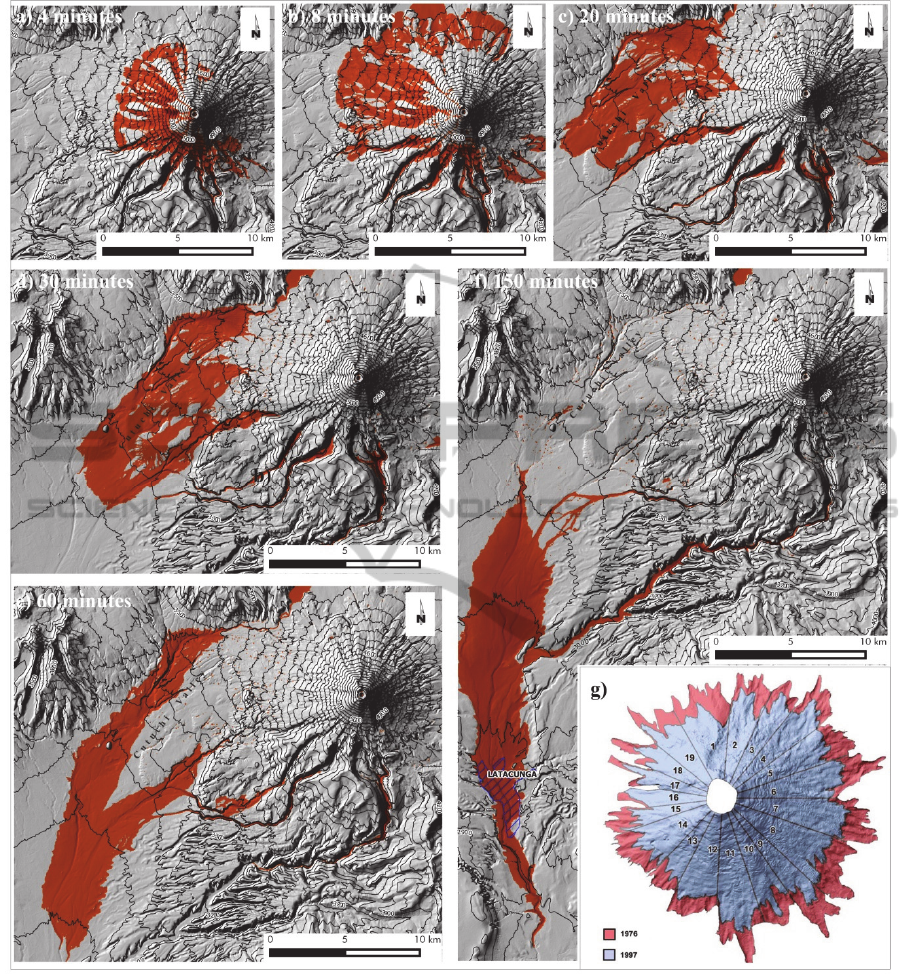
Figure 6: a), b), c), d), e), f) Time steps of glacier melting simulation by trigger moment; g) 1976 glacier extension

considered in simulation (from Cáceres et al. 2004).

sequentially in the same order as in section 3.

Parallelism was not explicitly activated and the

simulation average time is now 5 days, because the

implementation of LLUNPIY is not optimized; an

optimisation is in progress, it will speed simulations

up to 2 days. A parallel version for GPGPU will be

developed when the model will be completed for

both primary and secondary lahars, in the same way

as Spataro et al. (2008).

Some points, which can be improved in the

future research work, have to be considered:

We operated on the current morphology; some

corrections have to be produced in order to approach

the pre-event morphology and to tune better the

parameters of LLUNPIY.

Initial velocity of the lahars in the case of “many

sources simulations” is null; such simulations can be

repeated, starting with an opportune velocity by

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

374

varying the model and introducing a “lahar source”;

The immediate melting of the Cotopaxi icecap

descends from the worst hypothesis among the

possible ones, regarding the first phase of the

phenomenon; it is important to test the other

hypotheses.

Anyway, the results of these preliminary

simulations demonstrate that the CA model

LLUNPIY is working appropriately, if we consider

the partial, sometime rough data concerning the

event (Mothes et al., 2014) and its possible

improvements.

The simulations were acceptable in terms of

reproducing the global dynamics of the events, such

as velocity and height of detrital flow. Simulated

lahar path and invaded area agree with real (partially

reconstructed) one.

Times are not respected: in simulations, lahars

reached Latacunga about 30 minutes later than

reported in the chronicles of the time (Wolf, 1878).

This discrepancy could depend on some imprecision

of chronicles or on the increased length of paths in

the simulation because of space discretisation or

both; we will investigate such a problem by

considering these different viewpoints.

Our main future goal concerns the simulation of

the overall phenomenon, considering the total icecap

melting or partial melting by the effect of pyroclastic

bombs. If data will be available, we plan simulating

lahars toward the Quito region and the production of

hazard scenarios for possible new eruptions of

Cotopaxi volcano.

ACKNOWLEDGEMENTS

The authors are grateful to Patricia Mothes,

Researcher at IGEPN for obtaining data concerning

the Cotopaxi volcano and 1877 eruption, useful

information, advices and comments.

The authors thank William Spataro and Maria

Vittoria Avolio for critical revision of the

manuscript, suggestions and useful advices.

REFERENCES

Avolio M. V., Crisci, G. M., Di Gregorio, S., Rongo, R.,

Spataro, W. G., Trunfio, A., 2006. SCIARA γ2: an

improved Cellular Automata model for Lava Flows

and Applications to the 2002 Etnean crisis. Computers

& Geosciences, vol 32.

Avolio, M. V., Crisci, G. M., D’Ambrosio, D., Di

Gregorio, S., Iovine, G., Rongo, R., Spataro, W., 2003.

An extended notion of Cellular Automata for surface

flows modelling. WSEAS Transactions on Computers.

Avolio, M. V., Di Gregorio, S., Lupiano, V., Mazzanti, P.,

2013. SCIDDICA-SS3: A New Version of Cellular

Automata Model for Simulating Fast Moving

Landslides. The Journal of Supercomputing,65.

SPRINGER.

Avolio, M. V., Di Gregorio, S., Lupiano, V., Mazzanti, P.,

Spataro, W., 2010. Application context of the

SCIDDICA model family for simulations of flow-like

landslides. In Proceedings of the 2010 international

conference on scientific computing, Las Vegas (USA).

Avolio, M. V., Di Gregorio, S., Spataro, W., Trunfio,

G.A., 2012. Theorem about the algorithm of

minimization of differences for multicomponent

cellular automata. In ACRI 2012, SPRINGER

VERLAG.

Avolio, M. V., Lupiano, V., Mazzanti, P., Di Gregorio, S.,

2008. Modelling combined subaerial-subaqueous

flow-like landslides by cellular automata. In ACRI

2008. SPRINGER VERLAG.

Avolio, M.V ., Lupiano, V., Mazzanti, P., Di Gregorio, S.,

2009. A Cellular Automata Model for Flow-type

Landslide with Simulations of Subaerial and

Subaqueous cases. In Proceedings of EnviroInfo 2009.

Berlin, Germany, vol. 1, p. 131-140.

Barclay, J., Alexander, J., Susnik, J., 2007. Rainfall-

induced lahars in the Belham Valley, Montserrat, West

Indies. Journal of the Geological Society, London 164.

Cáceres B., Ramírez J., Francou B., Eissen J.P., Taupin J.

D., Jordan E., Ungerechts L., Maisincho L., Barba D.,

Cadier E., Bucher R., Peñafiel A., Samaniego P.,

Mothes P., 2004. Determinación del volumen del

casquete de hielo del volcán Cotopaxi. Informe

INAMHI, IRD, IG-EPN, INGEOMINAS.

Costa, J. E., 2004. Hydraulic modeling for lahar hazards at

Cascades volcanoes. Environmental and Engineering

Geosciences £.

Crisci G. M., Di Gregorio S., Rongo R., Spataro W., 2005.

PYR: a Cellular Automata model for pyroclastic flows

and application to the 1991 Mt. Pinatubo eruption,

Future Generation Computer Systems, 21.

D’Ambrosio, D., Di Gregorio, S., Gabriele, S., Gaudio, R.,

2001. A Cellular Automata Model for Soil Erosion by

Water. Physics and Chemistry of the Earth, EGS, Part

B 26(1).

Di Gregorio, S., Serra R., 1999. An empirical method for

modelling and simulating some complex macroscopic

phenomena by cellular automata. Future Generation.

Computer Systems.

Hoblitt, R. P., Miller, C. D., Scott, W. E., 1987. Volcanic

Hazards with Regard to Siting Nuclear-Power Plants

in the Pacific Northwest. U.S. Geological Survey

Open-File Report.

Lupiano V., Avolio M. V., Anzidei M., Crisci G. M., Di

Gregorio S., 2014a. Susceptibility Assessment of

Subaerial (and/or) Subaqueous Debris-Flows in

Archaeological Sites, Using a Cellular Model. In

Lollino G. et Al. (Eds.) Engineering Geology for

Society and Territory, - Volume 8, pp 405-408

LLUNPIYPreliminaryExtensionforSimulatingPrimaryLahars-Applicationtothe1877CataclysmicEventofCotopaxi

Volcano

375

Springer Verlag. DOI: 10.1007/978-3-319-09408-

3_70.

Lupiano V., Avolio M. V., Di Gregorio S., Peres D. J.,

Stancanelli L. M., 2014b. Simulation of 2009 debris

flows in the Peloritani Mountains area by SCIDDICA-

SS3. Proceeding of 7th WSEAS International

Conference on Engineering Mechanics, Structures,

Engineering Geology, Salerno (Italy), pp. 53-61,

ISBN: 978-960-474-376-6.

Machado, G., Lupiano, V., Avolio, M. V., Gullace, F., Di

Gregorio, S., 2015. A cellular model for secondary

lahars and simulation of cases in the Vascún Valley,

Ecuador. Submitted to Journal of Computational

Science.

Machado, G., Lupiano, V., Avolio, M. V., Di Gregorio, S.,

2014. LLUNPIY: Un modelo de Autómatas Celulares

para la simulación de Lahares Secundarios, In II

Wordshop de Ciencia, Innovación, Teconología y

Saberes, At Universidad Nacional de Chimborazo,

Riobamba, Ecuador.

Machado, G., Lupiano, V., Avolio, M. V., Di Gregorio, S.,

2014. A Preliminary Cellular Model for Secondary

Lahars and Simulation of 2005 Case of Vascún

Valley, Ecuador, In ACRI 2014, SPRINGER

VERLAG.

Major, J. J., Pierson, T. C., Dinehart, R. L., Costa, J. E.,

2000. Sediment yield following severe volcanic

disturbance a two-decade perspective from Mount St.

Helens. Geology, 28.

Manville, V., Hodgson, K. A., Houghton, B. F., Keys, J.

R. H., White, J. D. L., 2000. Tephra, snow and water:

complex sedimentary responses at an active snow-

capped stratovolcano, Ruapehu, New Zealand. Bulletin

of Volcanology, 62.

Manville, V., Major, J. J., Fagents, S. A., 2013. Modeling

lahar behavior and hazards, In: Modeling Volcanic

Processes The Physics and Mathematics of Volcanism,

Cambridge University Press, Cambridge.

Mothes, P., Vallance, J. W., 2014. Volcanic Hazards,

Risks, and Disasters, In Lahars at Cotopaxi and

Tungurahua Volcanoes, Ecuador, Elsevier Inc., New

York.

Muñoz-Salinas, E., Castillo-Rodríguez, M., Manea, V.,

Manea, M., Palacios, D., 2009. Lahar flow simulations

using LAHARZ program: application for the

Popocatépetl volcano, Mexico. J. Volcanol. Geotherm.

Res. 182.

O'Brien, J. S., Julien, P. Y., Fullerton, W. T., 1993. Two-

dimensional water flood and mudflow simulation. J.

Hydraul. Eng. ASCE 119 (2).

Pierson, T. C., Janda, R. J., Thouret, J. C., Borrero C. A.,

1990. Perturbation and melting of snow and ice by the

13 November 1985 eruption of Nevado del Ruiz,

Colombia, and consequent mobilization, flow and

deposition of lahars. J. Volcanol. Geotherm.

Pistolesi, M., Cioni, R., Rosi, M., Aguilera, E., 2014.

Lahar hazard assessment in the southern drainage

system of Cotopaxi Volcano, Ecuador: Results from

multiscale lahar simulations. Geomorphology 207.

Pitman, E. B., Nichita, C. C., Patra, A. K., Bauer, A. C.,

Sheridan, M. F., Bursik, M., 2003. Computing

Granular Avalanches and Landslides. Physics of

Fluids 15(12) Press, United States.

Schilling, S. P., 1998. LAHARZ: GIS Programs for

Automated Mapping of Lahar-inundation Hazard

Zones: U.S. Geological Survey Open-File Report 98-

638.

Smith, G. A., Fritz, W. J., 1989. Volcanic influences on

terrestrial sedimentation. Geology.

Sodiro, L., 1877. Relación sobre la eupción del Cotopaxi

acaecida el dia 26 de Junio de 1877. Imprenta

Nacional, Quito, Ecuador.

Spataro, W., D'Ambrosio, D., Spingola, G., Zito, G.,

Rongo, R., 2008. libAuToti, A Parallel Cellular

Automata Library for Simulation: An example of

Application to Landslides. Proceedings of the 2008

Summer Computer Simulation Conference, June 16-

19, 2008, Edinburgh, UK.

Vallance, J. W., 2000. Lahars. In: Sigurdsson, H. (Ed.),

Encyclopedia of Volcanoes. Academic.

Vallance, J.W., 2005. Volcanic debris flows. In Debris

Flow Hazards and Related Phenomena. Praxis-

Springer, Berlin and Heidelberg.

Williams, R., Stinton, A. J., Sheridan, M. F., 2008.

Evaluation of the Titan2D two-phase flow model

using an actual event: Case study of the 2005 Vazcún

Valley Lahar, Journal of Volcanology and Geothermal

Research 177.

Wolf, T., 1878. Memoria sobre el Cotopaxi y su Última

Erupción Acaecida el 26 de Junio de 1877. Imprenta

del Comercio, Guayaquil, Ecuador.

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

376