
Optimization of Parallel-DEVS Simulations with Partitioning Techniques
Christopher Herbez
1
, Eric Ramat
1
and Gauthier Quesnel
2
1
LISIC, ULCO, 50 rue Ferdinand Buisson, 62228 Calais, France
2
INRA MIAT, 24 chemin de Borde Rouge Auzeville, 31326 Castanet-Tolosan, France
Keywords:
Parallel simulation, Graph partitioning, Parallel-DEVS, Multithreading.
Abstract:
With the emergence of parallel computational infrastructures at low cost, reducing simulation time becomes
again an issue of the research community in modeling and simulation. This paper presents an approach to
improve time of discrete event simulations. For that, the Parallel Discrete EVent System formalism is coupled
to a partitioning method in order to parallelize the graph of models. We will present the graph partitioning
method to realize this cutting and quantify the resulting time savings of parallel implementation. This article
highlights the importance of considering the dynamic of the model when partitioning to improve performances.
Many tests are performed from graphs with different sizes and shapes on several hardware architectures.
1 INTRODUCTION
Modeling complex systems are becoming increas-
ingly costly in time and memory capacity, it is nec-
essary to develop efficient modeling and simulation
tools to address them. DEVS formalism (Zeigler
et al., 2000) and Parallel-DEVS variant (Chow, 1996)
Discrete Event Specification is a good candidate to de-
velop a response to both formal and technical. That
i-s a discrete events modeling and simulation the-
ory with a hierarchical approach. The global model,
called structure of the model in DEVS terminology, is
a graph of coupled models. We propose to work from
this models graph to optimize the simulation.
The use of parallel and distributed infrastructure
can make a efficient response of optimization prob-
lem. Our approach is to use a partitioning algorithm
on the graph models in order to parallelize their exe-
cution as efficiently as possible.
In (Herbez et al., 2015), we presented this ap-
proach as well as the relative gains obtained for two
types of partitioning. One is based on the connectiv-
ity of the graph, and the other is oriented modeler. In
these examples, the gain obtained by the introduction
of a good partitioning is about 20% compared to an
initial model hierarchy.
The goal of this paper is to show how partitioning
is used to optimize the Parallel-DEVS structure in-
cluding through load balancing between threads and
minimization of exchanges between them. We will
also show the limitations of this approach, and pro-
pose ways to address them. To achieve this, tests are
carried out for two types of graphs and multiple hard-
ware architectures.
In the first part, we describe the Parallel-DEVS
formalism and partitioning graph method used for our
tests. Then, various tests on several hardware archi-
tectures will be presented by illustration of the results.
The results will be analyzed to show that it is possible
to evaluate retrospectively the parallel capabilities of
the models. And finally, a discussion will attempt to
suggest ways to improve the method.
2 FORMALISMS AND METHODS
In this section, the Parallel-DEVS formalism is for-
mally presented and through the main algorithms
for implementation of the formalism. Moreover, we
present the graph partitioning method chose to opti-
mize the Parallel-DEVS simulations.
2.1 Parallel-DEVS
DEVS (Discrete Event Specification) (Zeigler et al.,
2000) is a high level formalism based on the discrete
events for the modeling of complex discrete and con-
tinuous systems. The model is a network of intercon-
nections between atomic and coupled models. These
models are in interaction via time-stamped events ex-
changes.
289
Herbez C., Ramat E. and Quesnel G..
Optimization of Parallel-DEVS Simulations with Partitioning Techniques.
DOI: 10.5220/0005543702890296
In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),
pages 289-296
ISBN: 978-989-758-120-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

More specifically, we present the Parallel-DEVS
(PDEVS) formalism (Chow and Zeigler, 1994; Chow,
1996). This extension of the classic DEVS introduces
the concept of simultaneity of events essentially by al-
lowing bags of inputs to the external transition func-
tion. Bags can collect inputs that are built at the same
date, and process their effects in future bags.
PDEVS defines an atomic model as a set of input
and output ports and a set of state transition functions:
M =
h
X,Y,S,δ
int
,δ
ext
,δ
con
,λ, ta
i
With: X, Y, S are respectively the set of input values,
output values and sequential states
ta : S → R
+
0
is the time advance function
δ
int
: S → S is the internal transition function
δ
ext
: Q ×X
b
→ S is the external transition function
where:
Q = {(s,e)|s ∈ S,0 ≤ e ≤ ta(s)}
Q is the set of total states,
e is the time elapsed since last transition
X
b
is a set of bags over elements in X
δ
con
: S × X
b
→ S is the confluent transition
function, subject to δ
con
(s,
/
0) = δ
int
(s)
λ : S → Y is the output function
If no external event occurs, the system will stay
in state s for ta(s) time. When e = ta(s), the system
changes to the state δ
int
. If an external event, of value
x, occurs when the system is in the state (s, e), the
system changes its state by calling δ
ext
(s,e,x). If it
occurs when e = ta(s), the system changes its state
by calling δ
con
(s,x).
Every atomic model can be coupled with one or
several other atomic models to build a coupled model.
This operation can be repeated to form a hierarchy of
coupled models. A coupled model is defined by:
N = hX,Y,D,{M
d
},{I
d
},{Z
i,d
}i
Where X and Y are input and output ports, D the
set of models and:
∀d ∈ D,M
d
is a PDEVS model
∀d ∈ D ∪ {N}, I
d
is the influencer set of d :
I
d
⊆ D ∪{N}, d /∈ I
d
,∀d ∈ D ∪ {N},
∀i ∈ I
d
,Z
i,d
is a function,
the i-to-d output translation:
Z
i,d
: X → X
d
, if i = N
Z
i,d
: Y
i
→ Y, if d = N
Z
i,d
: Y
i
→ X
d
, if i 6= N and d 6= N
The influencer set of d is the set of models that
interact with d and Z
i,d
specifies the types of relations
between models i and d.
PDEVS is an operational formalism. This means
that the formalism is executable and thus it provides
algorithms for its execution. These algorithms define
the sequence of the different functions of the PDEVS
structure. Moreover, the atomic and coupled models
are respectively associated with simulators and co-
ordinators. The aim of simulators is to compute the
various functions while the coordinators manage the
synchronization of exchanges between simulators (or
coordinators in a hierarchical view).
Figure 1: Hierarchy of coordinators and simulators. Black
box is the root coordinator (manage simulation), Grey boxes
are coordinators (simulate coupled models) and white boxes
are simulators (simulate atomic models).
2.2 PDEVS Algorithms
In this article, we explain the PDEVS abstract sim-
ulators especially the algorithms of the coordinator
which allows concurrent simulation between the com-
ponents of the coordinator. Indeed, the Parallel-
DEVS approach to parallelize simulation uses a risk-
free and strict causality adherence. It uses a global
minimum time synchronization and allows a concur-
rent and simultaneous output collection and distribu-
tion of events
Algorithm 1: Parallel-DEVS-Coordinator.
1: procedure VARIABLES
2: DEV S = (X ,Y,D,{M
d
},{i
d
},{Z
i,d
})
3: parent: parent coordinator
4: tl, tn
5: event − list: list of elements (d,tn
d
) sorted
6: IMM: imminent children
7: mail: output mail bag
8: y
parent
9: {y
d
}
In Figure 1, coordinator are represented by the
grey boxes. Each coordinator manages a scheduler
and route messages between children. The scheduler
stores internal events (one internal event per child)
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
290

sorted by time to wake up models. These times are
produced using the ta function for atomic models and
the current date of the simulation. For each itera-
tion, coordinator build a set of immediate message (all
events with the same wake up time).
Algorithm 2: Parallel-DEVS-Coordinator.
1: procedure WHEN RECEIVE I-MESSAGE(i, t) AT
TIME t
2: for each d ∈ D do
3: send i-message to child d in parallel way
4: sort event-list according to tn
d
5: tl = max{tl
d
|d ∈ D}
6: tn = min{tn
d
|d ∈ D}
Algorithm 3: Parallel-DEVS-Coordinator.
1: procedure WHEN RECEIVE *-MESSAGE(∗, t)
2: if t 6= tn then
3: error: bad synchronization
4: IMM = {d|(d,tn
d
) ∈ (event-list ∧tn
d
= tn)}
5: for each r ∈ IMM do
6: send *-message (*, t) to r in parallel way
Algorithm 4: Parallel-DEVS-Coordinator.
1: procedure WHEN RECEIVE X-MESSAGE(x, t)
2: if ¬(tl 6 t 6 tn) then
3: error: bad synchronization
4: receivers = {r|r ∈ D, N ∈ I
r
,Z
N,r
(x) 6=
/
0}
5: for each r ∈ receivers do
6: send x-message (Z
N,r
(x), t) to r in parallel
way
7: for each r ∈ IMM ∧ ¬ ∈ receivers do
8: send x-message (
/
0, t) to r in parallel way
9: sort event-list according to tn
d
10: tl = t
11: tn = min{tn
d
|d ∈ D}
Messages received by a coordinator are described
in the algorithms 1, 2, 3, 4 and 5. i-message is used
to initialize children. *-message is used to compute
output of children. x-message and y-message are
used to route messages. In PDEVS, all imminents
(IMM) are allowed to execute concurrently in con-
trast to DEVS where imminents were sequentially ac-
tivated. The outputs of IMM are collected into a bag
called the mail in previous algorithms. The mail is an-
alyzed for the part going out because of the EOC and
the parts to be distributed internally to the components
due to the IC coupling. The internal transition func-
tions of the imminents are not executed immediately
since the may also receive input at the same model
time.
Algorithm 5: Parallel-DEVS-Coordinator.
1: procedure WHEN RECEIVE Y-MESSAGE(y
s
, t)
WITH OUTPUT y
d
FROM d
2: if this is not the last d in IMM then
3: add (y
d
, d) to mail
4: mark d as reporting
5: else
6: if this is the last d ∈ IMM then
7: y
parent
=
/
0
8: for each d ∈ I
N
∧ d is reporting do
9: if Z
d,N
(y
d
) 6=
/
0 then
10: add y
d
to y
parent
11: send y-message(y
parent
, t) to parent
12: for each child r with some d ∈ I
r
∧d is report-
ing ∧Z
d,r
(y
d
) 6=
/
0 do
13: for each d ∈ I
r
∧ d is reporting
∧Z
d,r
(y
d
) 6=
/
0 do
14: add Z
d,r
(y
d
) to y
r
15: send x-message(y
r
,t) to r
16: for each r ∈ IMM ∧ y
r
=
/
0 do
17: send x-message(
/
0,t) to r
18: sort event-list according to tn
d
19: tl = t
20: tn = min{tn
d
|d ∈ D}
2.3 Graph Partitioning and Parallel
Mode
Using graph partitioning to transform the model hier-
archy in another in order to be optimized for parallel
simulations, this work is possible thanks to the clo-
sure under coupling property of DEVS (Zeigler et al.,
2000). This property formally describes the coupled
model is equivalent to an atomic model. Thus an
atomic model can be move into a new coupled model
and all the hierarchy of coupled model can be merge
into a unique coupled model.
The result of the coupled model hierarchy merge
give an oriented graph. In mathematics, a graph is de-
fined by G = (V, E) where V is the vertices set and
E the edges set. For the simulation, V describe the
atomic models and E the connection network between
them. Moreover, a weight could be associated to each
vertex and edge. For vertices, the weight quantify the
execution time and for edges quantify the data propor-
tion transmitted between models. Slower is a model,
bigger is his weight.
The k-way graph partitioning allows to cut a graph
G into k subgraphs {G
1
,G
2
,. .. ,G
k
}, while minimiz-
OptimizationofParallel-DEVSSimulationswithPartitioningTechniques
291

ing one or more criterion. They are represented by
functions named “objective function”. This cutting
provides k subsets of vertices P
k
= {V
1
,V
2
,. .. ,V
k
} ⊂
V named partition. Each vertex of a part V
i
is executed
on the same simulation node or logical process (LP).
For reduce the simulation time, it’s necessary equal-
ize the execution time on each LP and minimize the
events exchange between them. This can be reflected
by the partition quality. To be good quality, a parti-
tion must respect some conditions: the parts weight
must be similar and connections between parts must
be minimal.
The objectives of our research are to reduce execu-
tion time for very large simulations (more than 20000
models). These simulations give very large model
graphs. It is necessary to use partitioning graph meth-
ods efficient for this graph size. We use a multilevel
scheme in order to solve the problem.
The following subsection present the objective
functions used for partitioning in order to minimize
the simulation time.
2.3.1 The Objective Function
The partition quality is given by the objective func-
tions. Smaller is the result, better is the partition qual-
ity. They revolve around two concepts: cost cutting
between partition parts and parts weight.
Given a partition P
k
= {V
1
,V
2
,...,V
k
}, the edge cut
of two parts is the weight sum of edges connecting V
1
and V
2
:
Cut(V
1
,V
2
) =
∑
v
1
∈V
1
,v
2
∈V
2
weight(v1,v2) (1)
For a partition P
k
, the edge cut is the weight sum
of edges connecting partition parts:
Cut(P
k
) =
∑
i< j
Cut(V
i
,V
j
) (2)
This objective function was already used by Brian
Kernighan and Shen Lin in (Kernighan and Lin,
1970).
Another function allows simultaneous manage-
ment the minimization of the edge cut and weight bal-
ance between parts: the ratio cut:
Ratio(P
k
) =
k
∑
i=1
Cut(V
i
,V −V
i
)
weight(V
i
)
(3)
It was introduced by Yen-Chuen Wei and Chung-
Kuan Cheng in (Wei and Cheng, 1989). In our works,
we seek to minimize this objective function.
2.3.2 The Multilevel Method
As introduce in (Herbez et al., 2015), we used a mul-
tilevel schemes to create quickly a graph partition of
big size. It consists of three phases:
• Coarsening: Graph reduction by successive ver-
tices matching, while keeping the nature of the
original graph. Iterative process generating a
graph base {G
1
,· ·· ,G
n
}, where G
1
= G the origi-
nal graph and G
n
the contracted graph. The Heavy
Edge Matching introduced in (Karypis and Ku-
mar, 1998) is implemented for this phase.
• Partitioning: Creating of a partition P
k
of the
coarsening graph G
n
using a partitioning heuris-
tic. We choose an expanding region method: the
Greedy Graph Growing Partitioning (Karypis and
Kumar, 1998).
• Uncoarsening: Projection of the partition P
k
on
each contraction graph levels G
i
(i = n − 1,...,1).
But after each projection it is necessary to realize
a refinement for keep a good quality. We use a
local optimization algorithm based on Kernighan-
Lin algorithm (Kernighan and Lin, 1970)
For convenience, the multilevel implementation
using GGGP as partitioning phase will be call GGGP.
3 DATA, SOFTWARE AND
HARDWARE
This section presents the data on which the tests were
conducted, as well as the different used hardware ar-
chitectures.
3.1 Data Description
Tests were realized from two classical graph types in-
spired by the water flow model: a grid and a “tree”
(abusively named). We have choose these names be-
cause they reflect the graph form, even if in the liter-
ature a “tree graph” is a hierarchical graph. It’ is not
the case here. For each graph, the vertices weight is
equal to 1 because the execution time of the models
is the same. The edge weight is equal to 1 because
the message transfer cost is the same between each
model. We work on large simulations, where graphs
have 20000 vertices. They are presented in Figure 2.
The left graph consists of several levels, where
there are a single vertex source and outlet. The ver-
tex source is the starting model of the simulation and
the outlet is the ending model. Each vertex of level n
is connected with two vertices of level n − 1. For the
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
292

penultimate level, vertices are connected only to the
outlet.
Figure 2: Little graphs size examples. On the left, a “grid
graph” and on the right a “tree graph” (abusively named).
The right graph is composed of several branches,
where each vertex is connected to one or more ver-
tices following a single direction. The branches are
branched until reaching the single outlet. This graph
have several source vertices on each top branch (n
sources by branches).
3.2 Software and Hardware
Architectures
The tests were performed on a PDEVS simula-
tion kernel written in C++11. This simulation ker-
nel is part of the VLE project (Virtual Laboratory
Environment) a modeling and simulation software
suite (Quesnel et al., 2009). The VLE software suite
is used in many projects in the French National In-
stitute for Agronomical Research and several French
Universities.
The simulations were done on an three different
hardware architectures:
• Intel Core i5-2520M processor - 2.5 GHz: 2 cores
with 4 threads (hyperthreading mode)
• Intel Core i7-3840QM processor - 2.8 GHz: 4
cores with 8 threads (hyperthreading mode)
• Samsung Exynos 5422 with a Cortex A15 2.1 Ghz
quad core and a Cortex A7 1.5 GHz quad core
processor: 4 big cores and 4 little cores
These four used architectures to test different al-
gorithms on architectures with different possibilities
in terms of cores. The smallest configuration allows
to have two cores with a small speedup factor of four
threads (2C + 2H). The second doubles possibilities
(4C + 4H). The third offers a hybrid solution (4C +
4LC) slightly greater than the second.
4 RESULTS AND DISCUSSION
In this section, we present simulation results on clas-
sical models which we employ in our scope (nitrogen
and water management in catchment area). For that,
PDEVS formalism and the partitioning algorithm, in-
troduced in section 2, are used on several hardware
architectures.
The results are then discussed to evaluated the
performance and limitations of our approach. These
tests are performed from the graphs presented in Sec-
tion 3.1.
4.1 Results Analysis
The simulation results presented in this subsection are
obtained for a computation time of about 1 ms by
models. Our goal is to compare the performance ob-
tained with those expected in theory.
In absolute terms, the expected performance for
parallelization tend to have a speedup equal to the
available thread number. It is named absolute theo-
retical speedup. However, given the dynamic of the
models, it is very difficult to achieve this performance
in pessimistic approach. In order to have an effective
comparison basis, we propose to compute a theoreti-
cal speedup including the dynamics of the models.
The following subsection present this theoretical
speedup and an illustration to explain its operation.
4.1.1 Theoretical Speedup Definition
For a given transition, the theoretical speedup is de-
fined by the ratio of the sum of active atomic models
and the maximum number of active models in one of
the coordinators. This is expressed mathematically
by:
Speedup =
k
∑
i=1
n
i
max
i∈{1,...,k}
n
i
(4)
where k is the coordinator number and n
i
the active
models number in the coordinator i.
The active models are the models included in the
IMM set when the transition function is executed.
The active models in a same coordinator form a bag.
For a given date, the bags size varies according to
the event propagation in the global model. If the bag
size is the same then the theoretical speedup is equal
to the number of active coordinators (since there is
OptimizationofParallel-DEVSSimulationswithPartitioningTechniques
293

one thread per coordinator and that, depending on the
hardware architecture, all threads can be executed in
parallel modulo the memory access). This concept is
illustrated in Figure 3.
M3
M2
M1
M4
M5
t
t
t
inf
T = t
Time step
inf
Mi
Mi
Part 1
Part 2
Schedulers
Root
C
C1 C2
M1
t
M2
t
M4
inf
M4
t
M1
t+1
M2
t+1
M1
t+1
M2
t+1
M4
inf
M1
t+1
M2
t+1
M4
inf
M3
t
M5
inf
T = t
T = t
T = t
T = t+1
M5
t
M3
inf
M5
t
M3
inf
M3
t+1
M5
inf
C1 C2
DEVS hierarchy
Caption
Active models
(bags)
Figure 3: Illustration of the schedulers evolution for a time
step on a small example.
This diagram shows different information from a
simulation at time t. The sub-diagram at top show a
graph models partitioned in two parts. His hierarchi-
cal representation is given at bottom on the left. Each
coordinator has a scheduler. Their evolution, for each
transition, is shown at the bottom right. Active mod-
els are represented by the shaded boxes. All active
models of a same coordinator form a bag. For the
first transition (M
1
,M
2
) and (M
3
) form two bags, so
the speedup of this transition is 1.5. The speedup is
computed for each transition. Here, there are 3 tran-
sitions with a respective speedup 1.5, 2 and 1.
For a give date t, n
t
-speedup are computed (n
t
is
the transition number). Figures 6 et 7 show this vari-
ation at the date t = 0. The theoretical speedup of a
date t is the mean of speedups at each transition:
Speedup(t) = mean(Speedup) (5)
And the speedup of the simulation is:
Theoretical
Speedup = mean(Speedup(t)) (6)
This theoretical speedup is closely linked to the
hierarchy of coordinators / simulators. It is important
to create balanced sub-models. But this is not enough,
it is necessary to have a balance between bags at each
transition to ensure a perfect balance. In our case, all
models have the same charge in terms of calculation,
that’s why we talk about model number and not model
weight.
4.1.2 Influence of the Hardware Architecture on
Speedup
Figures 4 and 5 compare the evolution of the speedup
for different hardware architectures to the theoretical
speedup. For that, we vary the number of threads (par-
tition number) and we observe the impact on the evo-
lution of the speedup.
Figure 4: Speedup for tree graphs with 3 hardware architec-
tures and theoretical speedup.
Figure 5: Speedup for grid graphs with 2 hardware archi-
tectures and theoretical speedup.
These curves show the influence of the hardware
architecture on the speedup. Indeed, until the number
of threads is less than or equal to the number of cores,
the speedup is very close to the theoretical value. For
architecture 4C + 4LC, a slight inflection is observed
with 8 threads because the 4 additional cores are less
efficient than the first 4 cores.
4.1.3 Link between Theoretical Speedup and
Partitioning Quality
The results presented in this subsection are obtained
from graph of size 1000 and a hierarchical structure
with four sub-models. The theoretical speedup can be
a partition quality indicator, as shows this subsection.
In the Figure 6, the transition function is com-
puted 63 times where 1/3 of them the number of ac-
tive sub-models is equal to 1. So the parallelization is
not used during this phase. By against, the remaining
two thirds show a efficiency close to the optimum (4).
Given the graphs structure, it is hard to beat.
For the grid (Figure 7), the conclusion is not the
same. We are far to the absolute theoretical speedup
with 4 threads (max = 2.2). This is explained by the
dynamics of the grid model: the events propagate by
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
294
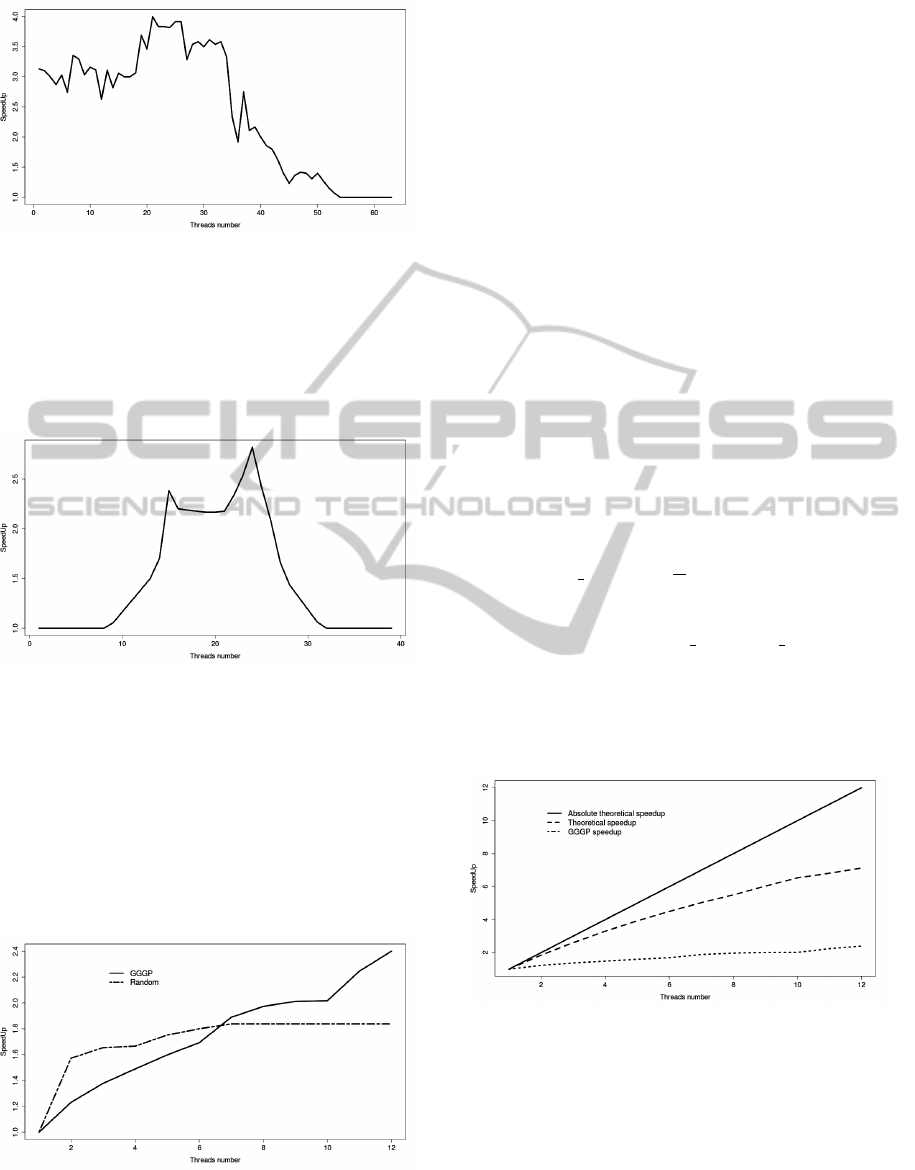
Figure 6: Variation of theoretical speedup at t = 0 for “tree”.
wave from the top left corner to the bottom right cor-
ner. For the partitioning, the grid is divided in 4 al-
most regular sub-grids. The number of models com-
puted in parallel can be at most 2 (or 3 in some limit
cases).
Figure 7: Variation of theoretical speedup at t = 0 for
“grid”.
Figure 7 suggests that partitioning is not optimal
in this case. It does not take sufficient account of the
dynamics of the model. However, the particular struc-
ture of this graph does that the theoretical speedup can
not always be equal to the absolute because the num-
ber of parallelizable models is lower than the number
of threads available at times. This is particularly the
case in the beginning and end of the simulation.
Figure 8: Speedup of gggp and random method on ”grid”.
To be convinced of the phenomenon, we generate
a random cutting and compare the theoretical speedup
that obtained with our partitioning method. Figure 8
shows that the random cutting has a greater theoretical
speedup for a parts number less than 8.
4.2 Results Discussion
The results show that in one case (tree), our partition-
ing method leads to the construction of a hierarchy
similar to the optimum of the theoretical speedup per-
spective. The second case (grid), the results are not
up to par. In fact, there are more suitable cuts which
follow the dynamics of the model. The optimal cut-
ting is computable and depends on the graph structure
and of the dynamics of the model. For each bag, di-
viding the cardinality of the IMM set by the number
of coordinators, we take the integer part. If the mod-
ulus of the two terms is not zero then added one (see
7). We then obtain the optimal size of bags that are
processed by each coordinator. The average is then
carried out on all the transitions (2N − 1 transitions
for a grid size N) for a time step. We obtain then
the theoretical speedup in optimum for the grid. The
equation of optimal speedup in this case is:
S bag(k) = b
k
P
c + hk mod Pi (7)
Speedup = mean(2
N−1
∑
i=1
S bag(i) + S bag(N)) (8)
We can then compare the theoretical speedup of
our partitioning compared to the theoretical speedup
of the best partitioning (see Figure 9).
Figure 9: Speedup comparison to the absolute for a ”grid”.
The objective of partitioning is to obtain a speedup
equal to the number of cores provided on the machine
during almost all of the simulation. To be a good
quality, the partition shall enable at the results to be
close to this speedup. Which is not actually our case
here. The partitioning method must not only balance
the loads among threads, it must also take into ac-
count the dynamics of the graph. The knowledge of
the dynamics minimizes the load difference between
OptimizationofParallel-DEVSSimulationswithPartitioningTechniques
295

the bags at each transition. This allows better man-
agement of threads throughout the simulation.
If the models were fully synchronous as in the
case of a cellular automaton, the issue of balanc-
ing would be easy to solve if all models have the
same computational load. In this case, we observe
no change in the number of transitions to be made be-
tween two time steps. The partitioning becomes use-
less. In contrast, if the models are completely asyn-
chronous, the IMM sets have a single model. Paral-
lelization is completely useless in a pessimistic con-
text. In this case, it was essential to work on algo-
rithms optimistic parallel simulation.
5 CONCLUSION AND
PROSPECTS
In this paper, we have shown that in some cases,
we improve the simulation time by using a partition-
ing based solely on the model structure. These sim-
ulations are performed using an implementation of
PDEVS algorithms in a risk-free mode. However, we
have shown that it is also necessary to consider the
dynamic of models for have a better models balance.
We have shown that the measure of the theoretical
speedup (see equation 4) based on the IMM set gives
us accurate information. We can generalize this mea-
sure so that it becomes an parallelization ability indi-
cator of a model. This indicator can vary from 1 to P
where P is the parts number of the graph. The mini-
mum value is obtained for fully asynchronous model
and the maximum value for fully synchronous model.
In our case, the indicator takes values close to the
maximum value. This means that a coupling between
a partitioning method and risk-free simulation is an
excellent approach. However, it is necessary to go fur-
ther if the indicator is close to 1. May be introduce a
conservative or optimistic simulation engine coupled
with partitioning methods. The model structure must
be consider, but also his dynamics and the conser-
vative algorithms with look-head properties (Chandy
and Misra, 1979; Chandy and Misra, 1981) or opti-
mistic (Time-Wrap (Jefferson, 1985), for example).
Look-head is the ability of a model to predict that it
will not have output for a certain period in future. The
complexity of the optimization algorithm will be in-
creased. It will be necessary to understand the interac-
tions between look-head, for example, dynamics and
the models graph.
Furthermore, our strategy of optimized hierarchy
building has the overall objective to integrate dis-
tributed hardware architecture where the communica-
tion time between processes are not negligible.
ACKNOWLEDGEMENTS
This work is carried out in research project named Es-
capade (Assessing scenarios on the nitrogen cascade
in rural landscapes and territorial modeling - ANR-
12-AGRO-0003) funded by French National Agency
for Research (ANR).
REFERENCES
Chandy, K. M. and Misra, J. (1979). Distributed simulation:
A case study in design and verification of distributed
programs. IEEE Trans. Software Eng., 5(5):440–452.
Chandy, K. M. and Misra, J. (1981). Asynchronous dis-
tributed simulation via a sequence of parallel compu-
tations. Commun. ACM, 24(4):198–206.
Chow, A. C.-H. (1996). Parallel devs: A parallel, hierarchi-
cal, modular modeling formalism and its distributed
simulator. Trans. Soc. Comput. Simul. Int., 13(2):55–
67.
Chow, A. C. H. and Zeigler, B. P. (1994). Parallel devs: A
parallel, hierarchical, modular, modeling formalism.
In Proceedings of the 26th Conference on Winter Sim-
ulation, WSC ’94, pages 716–722, San Diego, CA,
USA. Society for Computer Simulation International.
Herbez, C., Quesnel, G., and Ramat, E. (2015). Building
partitioning graphs in parallel-devs context for paral-
lel simulations. In Proceedings of the 2015 Spring
Simulation Conference.
Jefferson, D. R. (1985). Virtual time. ACM Trans. Program.
Lang. Syst., 7(3):404–425.
Karypis, G. and Kumar, V. (1998). A fast and high qual-
ity multilevel scheme for partitioning irregular graphs.
SIAM J. Sci. Comput., 20(1):359–392.
Kernighan, B. W. and Lin, S. (1970). An efficient heuristic
procedure for partitioning graphs. Bell System Techni-
cal Journal, 49(2):291–307.
Quesnel, G., Duboz, R., and Ramat, E. (2009). The Virtual
Laboratory Environment – An operational framework
for multi-modelling, simulation and analysis of com-
plex dynamical systems. Simulation Modelling Prac-
tice and Theory, 17:641–653.
Wei, Y.-C. and Cheng, C.-K. (1989). Towards efficient
hierarchical designs by ratio cut partitioning. In
Computer-Aided Design, 1989. ICCAD-89. Digest of
Technical Papers., 1989 IEEE International Confer-
ence on, pages 298–301.
Zeigler, B. P., Kim, D., and Praehofer, H. (2000). Theory of
modeling and simulation: Integrating Discrete Event
and Continuous Complex Dynamic Systems. Aca-
demic Press, 2nd edition.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
296
