Nonlinear Control Design of VSC-MTDC Systems based on

Backstepping Approach

Mohamed Ayari

, Mohamed Moez Belhaouane

1,2

, Xavier Guillaud

and Naceur Benhadj Braiek

Advanced Systems Laboratory, Polytechnic School of Tunisia (EPT), University of Carthage,

BP. 743, 2078, La Marsa, Tunis, Tunisia

Laboratory of Electrical Engineering and Power Electronic (L2EP),

Ecole Centrale de Lille, BP 48, 59851 Villeneuve d’Ascq Cedex, France

Keywords:

VSC, HVDC, Nonlinear Backstepping Control Approach, Lyapunov Theory, Active Power Control Mode,

DC Voltage Control Mode.

Abstract:

This paper deals with the nonlinear control approach of Voltage Source Converter (VSC) based on MTDC

(multi-terminal direct current) transmission systems. A nonlinear control approach based on Backstepping

method is proposed for two different control methods: active power and DC voltage. The proposed control

approach, based on Lyapunov theory, is capable of analytically obtaining a control laws in order to regulate

the active power and dc bus voltage in an MTDC system. Furthermore, the dynamic interactions between the

active power nonlinear control design and the DC voltage droop control are examined. Finally, the validity

of the proposed control design approach is veriﬁed by time-domain simulations under the Matlab/ Simulink

environment.

1 INTRODUCTION

The development of the renewable energy requires a

reliable technology for transmission power over long

distances. Since of the disadvantage of the High Volt-

age Alterning Current (HVAC) and with the progres-

sion of the power electronics, the High Voltage Direct

Current (HVDC) technology is improved in (Setr

eus

and Bertling, 2008). The high power self-commutated

VSC, based on the Gate-Turn-Off (GTO) and Insu-

lated Gate Bipolar Transistor (IGBT) using the Pulse

Width Modulation (PWM) techniques, are the princi-

pal components in the transmission system HVDC. To

this end, they are used serve to providing high qual-

ity AC output voltage to the grid or even to a passive

load, and facilitate the control of the strongly coupled

nonlinear system (Jovic et al., 2003).

The VSC based multiterminal VSC-HVDC power

transmission system (VSC-MTDC) is an ideal ap-

proach to connect more then two HVDC station by a

DC grid (Jacobson, 2011). Recently, the new Mod-

ular Multilevel Converter (MMC) is attractive for

HVDC applications thanks to its modular structure

(Belhaouane et al., 2014).

Many research have been discussed the model-

ing and control of a VSC-MTDC transmission sys-

tem (Chen et al., 2006). Traditionally, the conven-

tional Proportional Integral PI controllers are used to

control the VSC-HVDC converters. However, the dy-

namic performance of such control scheme is poor,

because of the strong interactions among the control

loops (Rashed et al., 2008). The strong nonlinearity

present in the system dynamics requires the use of

nonlinear control techniques. Thus, a large number

of controller for HVDC transmission systems based

on different control techniques have been proposed to

enhance the transient systems and dynamic stability.

Several nonlinear control techniques are used to over-

come difﬁculties during abnormal operating condi-

tions especially under parametric uncertainties, faults

and non-linear disturbances (Ramadan et al., 2012).

Further, the application of advanced nonlinear

controls that is: robust control (Ramadan et al.,

2008), (Moharana and Dash, 2010), optimal control

(Sachdev et al., 1973), adaptive control (Reeve and

Sultan, 1994), and controls-based on artiﬁcial intel-

ligence (AI) (Dash et al., 1999), (Moharana et al.,

2006), have been developed for improving transient

stability of power systems (Colbia-Vega et al., 2008).

These approaches are used to elaborate complex non-

linear controllers, characterized by a lack of complete

knowledge of the dynamic characteristics of the sys-

tem.

Recently, the Backstepping control design tech-

596

Ayari M., Belhaouane M., Guillaud X. and Benhadj Braiek N..

Nonlinear Control Design of VSC-MTDC Systems based on Backstepping Approach.

DOI: 10.5220/0005545305960602

In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 596-602

ISBN: 978-989-758-122-9

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

niques have received an important attention because

of its systematic and recursive design methodol-

ogy for nonlinear feedback control (Jammazi, 2008),

(Kim and Kim, 2003). In (Ruan et al., 2007), an

adaptive Backstepping control method is proposed

and uncertainties of AC grid current is considered.

(Wang et al., 2013) proposed a Backstepping control

design to ensure the stability of VSC-HVDC system

in case of a parameter variations and external distur-

bances. To control an MTDC system, a feedback lin-

earization strategy and Backstepping-like procedure

are proposed in (Chen et al., 2013).

In this manuscript, an integral Backstepping con-

trol scheme is presented and applied on a multi-

terminals VSC-HVDC transmission systems in order

to regulate the reactive power, active power and the

DC voltage where an integral action is added to en-

sure zero steady -state tracking error.

This paper is structured as follows. The math-

ematic model of VSC-MTDC station is given in 2.

Based on Lyapunov theory, an integral Backstepping

controller for each control mode is depicted in 3. Sec-

tion 4 presents the simulation results by using Mat-

lab/Simulink environment. At last, Conclusions are

drawn in Section 5.

2 MODELING OF VSC-MTDC

SYSTEM

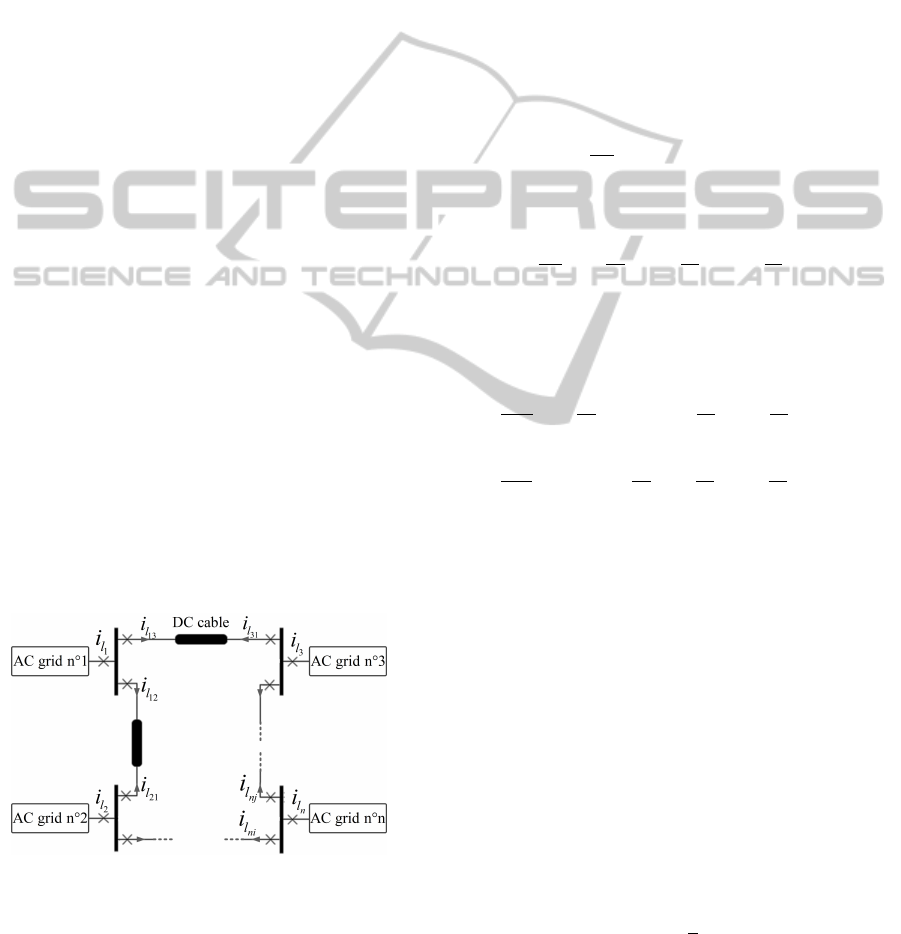
In Fig. (1), the topology of Multi-terminal VSC-

MTDC for interconnexion between n AC networks

is depicted. It consists of DC cables with different

length, identical voltage source converters (VSCs),

and AC grids.

Figure 1: The interconnection between n terminals.

The conﬁgurations of the VSCs converter stations

are identical. In Fig. 2, one VSC terminal is shown.

and R

denote the inductance and the equivalent

resistance of the converter inductor respectively.

and ~u

represent respectively the three phase AC

current and the voltages of the both side of the reactor

phase. The control of an MTDC transmission systems

consist to control the VSCs converter either by DC

bus voltage droop control mode ”Us-Control” or AC

power control mode ”Pac-Control”. The Pac-Control

mode aim to control the active and reactive powers.

The Us-Control mode allows to maintain the balance

between power production and demand.

2.1 Average Model: Pac-Control Mode

The basic structure of the three phase VSC converter

is depicted in Fig. 2. In Pac-Control mode, The DC

voltage is considered ﬁx. Applying Kirchhoff’s volt-

age and current laws, it easy to obtain.

+ R

= −~u

+~u

(1)

Multiplying each term of the equation (1) by the Park

matrix P

, it follows that:

= −

−

(2)

where P

is the park transformation.

According to (2), the mathematical model of a VSC-

HVDC station operating on Pac-Control mode is writ-

ten as follows:

= −

+ ωi

−

= −ωi

−

(3)

where i

, i

are the dq components of the VSC out-

put current, u

, u

and u

, u

are the dq compo-

nents of the VSC output voltage, AC network voltage

respectively.

2.2 Average Model: Us-Control Mode

In the ”Pac-Control mode” presented above, the DC

voltage is considered as constant voltage variable and

presented by a ﬁxed voltage DC source. Referring

to Fig. 2 with the DC circuit ”Us-Control”, the DC

source is replaced now by the capacitor equivalent C

and current source.

By assuming a dq frame orientation such that

= 0 pu and neglecting the power losses on both

sides of the VSC converter, we get (Thomas et al.,

2001) :

= P

=⇒ u



+ u



(4)

where i

is the DC output current.

Using Eq. (3)-(4), we can obtain the following av-

erage model of the VSC-HVDC station operating on

NonlinearControlDesignofVSC-MTDCSystemsbasedonBacksteppingApproach

597

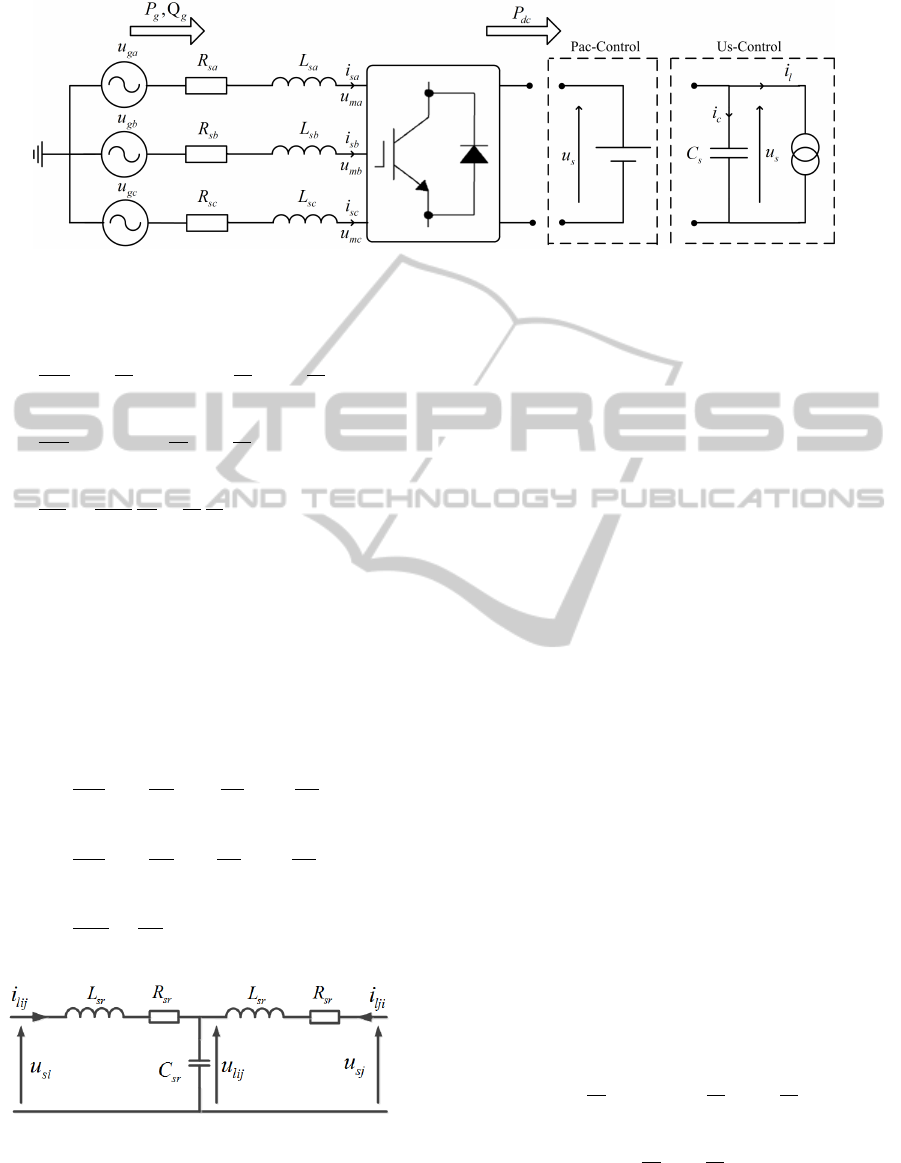
Figure 2: Basic structure of VSC converter.

Us-Control mode:











= −

+ ωi

−

= −ωi

−

(5)

2.3 DC Cable Model

The model of the DC transmission line connected to

the DC side of i

and j

stations, is an equivalent

circuit of T-type. L

, R

and C

denote respectively

the equivalent inductance, resistance and capacitance

of the cables. Then, the model of the DC cables is

described as:











i j

= −

i j

−

i j

= −

−

i j



i j

+ i



(6)

Figure 3: Simpliﬁed structure of DC cable (Thomas et al.,

2001).

3 INTEGRAL BACKSTEPPING

CONTROL SCHEME FOR

VSC-MTDC SYSTEMS

In this section, we propose a backstepping control

strategy including an integral action to ensure zero

steady-state tracking error. The proposed backstep-

ping controller is designed to keep the non-linearities

useful to enhance the performance and robustness of

control, unlike linearization methods. The determina-

tion of the control laws resulting from this approach

is based on Candidate Lyapunov Functions (CLF)

(Khalil, 2002), (Skjetne and Fossen, 2004).

The control purpose of an MTDC System is to reg-

ulate the DC voltage and to keep the power ﬂow at its

reference value. The ﬁrst VSC terminal controlling

both active and reactive powers, and all other termi-

nals are endowed with voltage droop controller (Dier-

ckxsens et al., 2012).

3.1 Integral Backstepping Controller of

Pac-control Mode

This control mode aims to regulate the active and re-

active powers. Considering the currents errors z

isd

and

isq

deﬁned by:

isd

= I

re f

− i

isq

= I

re f

− i

(7)

Differentiating z

isd

and z

isq

with respect to time gives:

˙z

isd

re f

− ωi

−

˙z

isq

re f

+ ωi

. (8)

where

re f

and

re f

are the time derivative of I

re f

and

re f

, respectively.

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

598

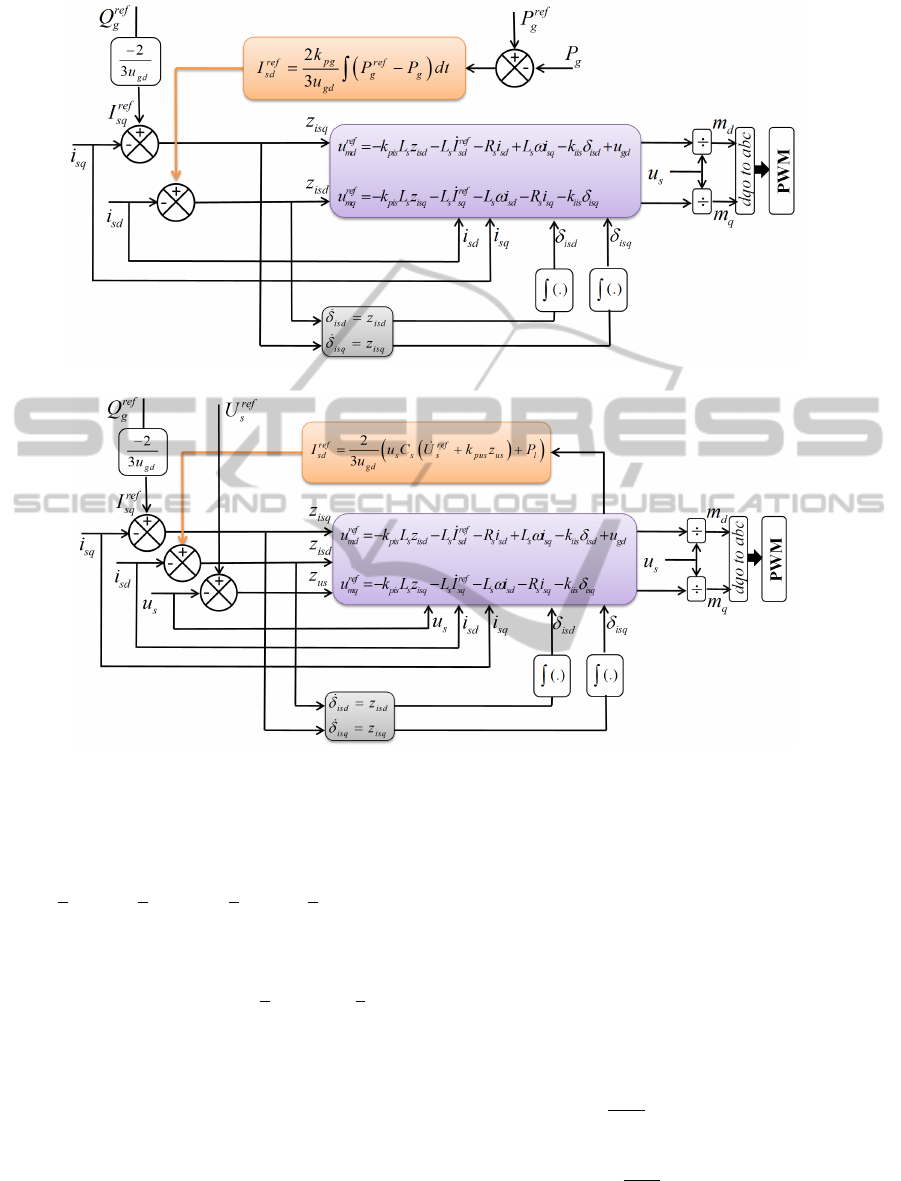
Figure 4: Block diagram of Backstepping method with integral action for P

-Control Mode.

Figure 5: Block diagram of Backstepping method with integral action for U

-Control Mode.

To investigate the stability of the errors model (7), a

Lyapunov function V

is chosen as:

isd

iis

isd

isq

iis

isq

(9)

where δ

isd

and δ

isq

are respectively the integral terms

of z

isd

and z

isq

, k

iis

> 0. The terms

isd

and

isq

represent the energy ﬂuctuation of the AC reactance.

The derivative of V

along the trajectories of (7) is

given by:

= z

isd



re f

+ R

− L

ωi

+ u

− u



+ z

isq



re f

+ L

ωi

+ R

+ u



iis

isd

+ k

iis

isq

(10)

which leads to the following control laws:

re f

= −k

pis

isd

− L

re f

− R

+ L

ωi

−k

iis

isd

+ u

re f

= −k

pis

isq

− L

re f

− L

ωi

− R

− k

iis

isq

(11)

yields:

= −k

pis



isd

+ z

isq



< 0 (12)

where k

pis

> 0.

The active and reactive powers are controlled through

the currents i

and i

respectively, such as:

re f



re f

− P



re f

= −

re f

(13)

The Backstepping control structure is deciped by Fig.

NonlinearControlDesignofVSC-MTDCSystemsbasedonBacksteppingApproach

599

3.2 Integral Backstepping Controller of

Us-droop Control Mode

In this section, a droop voltage controller is designed

to stabilize the DC voltage, decoupling the dq grid

current and regulate the reactive power.

We consider the mathematical model given in (5).

Firstly, we introduce z

= U

re f

− u

, z

isd

= I

re f

− i

isq

= I

re f

− i

isd

= z

isd

and

isq

= z

isq

The time derivative of z

is given as:

˙z

re f

−

re f

(14)

Let consider the following deﬁnite positive Lyapunov

function:

(15)

such that

represents the energy ﬂuctuation in

the dc capacitor.

From the equation (5), the derivative of V

along the

trajectories of the system is given by:

= C

re f

−

re f

(16)

Then, if z

isd

= 0 and following the backstepping

method in order to ensure stability of the tracking

voltage, the virtual control law I

re f

is given by the

following equation:

re f



re f

+ C

pus

+ P



(17)

Based on the above analysis, we get

as negative

semideﬁnite function expressed as:

= −k

pus

< 0 , k

pus

> 0 (18)

After the conception of the virtual controller, the sec-

ond step is to ensure the asymptotic stability of the

global system via the direct Lyapunov method based

on the new CLF. Then, differentiating the currents er-

rors z

isd

and z

isq

with respect to time yields:

˙z

isd

re f

− ωi

−

˙z

isq

re f

+ ωi

. (19)

where

re f

and

re f

are the time derivative of I

re f

and

re f

, respectively.

The candidate Lyupanov Function chosen for the

asymptotic stability of the global system is expressed

as:

= V

isd

iis

isd

isq

iis

isq

(20)

where k

iis

> 0.

The derivative of V

is given by:

= z

isd



re f

+ R

− L

ωi

+ u

− u



+ z

isq



re f

+ L

ωi

+ R

+ u



iis

isd

+ k

iis

isq

− k

pus

(21)

Similarly, by choosing the control laws as:

re f

= −k

pis

isd

− L

re f

− R

+ L

ωi

−k

iis

isd

+ u

re f

= −k

pis

isq

− L

re f

− L

ωi

− R

− k

iis

isq

(22)

, expressed by (23), is negative semideﬁnite.

= −k

pus

− k

pis

isd

− k

pis

isq

< 0 (23)

where k

pis

> 0.

Fig. 5 shows the structure of the control sys-

tem derived from the second step of the Backstepping

technique.

4 VALIDATION OF THE

PROPOSED NONLINEAR

CONTROL METHOD

To prove the effectiveness of the proposed control

strategy, a simulation study was carried out under

Matlab/Simulink environment. The test system is de-

picted in Fig. 6. It’s composed on two onshore and

offshore stations. It is worth pointing that each VSC

converter is rated at 1000 MVA, 320 kVrms phase to

phase AC voltage and a DC voltage of ± 320 kV.

Figure 6: A three-terminal VSC-HVDC transmission sys-

tem (Rault, 2014).

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

600

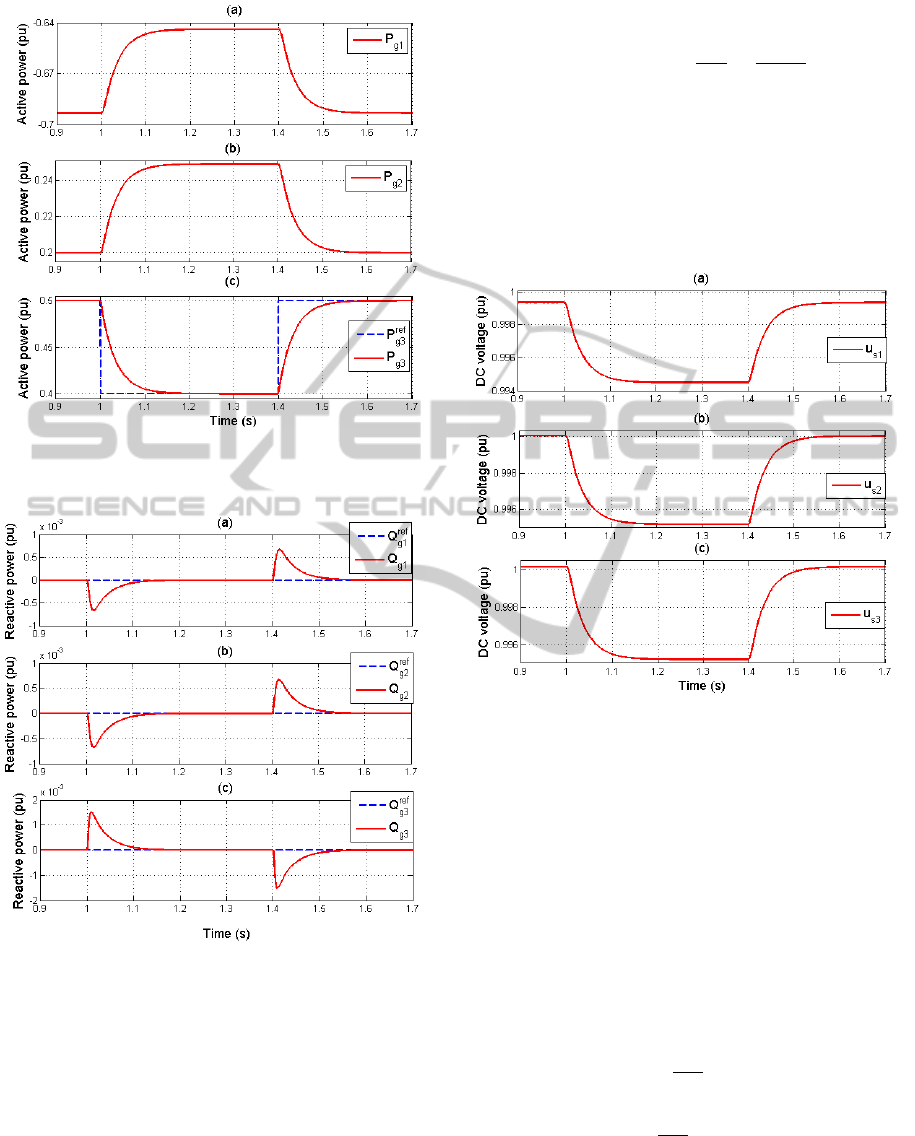
Figure 7: Behaviors of the active powers in the station n

◦

2 and n

◦

Figure 8: Behaviors of the reactive powers in the station n

◦

1, n

◦

2 and n

◦

The major contribution is based on the control de-

sign devoted to endow the station n

◦

1 and station n

◦

with the Us-droop control as well as controlling the

power ﬂow via the station n

◦

The control gains (k

pus

= 500, k

= 30,

pis

= 10

and k

iis

= 119.36) are synthesised in

order to ensure a response time for the grid currents

around 10 ms, a response time for the active power

equal to 100 ms and to deﬁne the droop value K to

adjust the power deviation portion which is following

through a converter station:







∆u

∆P

pus

(24)

where:

• K is the droop value;

• ∆P

is deviation of power injected into the AC

grid;

• ∆u

is deviation of DC voltage.

Figure 9: DC voltage behavior in the stations n

◦

1, n

◦

2 and

◦

Figs. (7)-(9) illustrate the behaviors of active power

and DC bus voltage for each stations. At instant t < 1

s, the power delivered by the wind farm is 0.5 pu (500

MW). The power injected through the station n

◦

2 to

the DC grid is 0.2 pu (200 MW) and the power ﬂow

from DC grid to AC grid through station n

◦

1 is 0.7 pu

(700 MW). For instants t between 1 s and 1.1 s, the

produced power by wind farm is decreased to 0.4 pu

(400 MW). This loss of production is equally shared

between the two onshore converter stations when they

have the same droop value:

= −700 +

100

= −650MW

= 200 +

100

= 250MW

As shown in Fig. 9, this event leads to decrease the

DC voltage level since there is less power transfer

with regard to the previous operating point.

Simulations results (not shown here) show that the

NonlinearControlDesignofVSC-MTDCSystemsbasedonBacksteppingApproach

601

direct and quadrature current are decoupled. From

Fig. 8, the reactive powers of each station is always

track the reference signal Q

re f

= 0 pu (i=1,2,3).

5 CONCLUSION

In this paper, the Backstepping control technique

based on direct Lyapunov method is extrapolated to

the VSC-MTDC application. The controller is able

to provide asymptotic stability for the power trans-

mission system with multiple terminals. The con-

trol law is based on a Backstepping-like procedure

which the stability of the whole transmission system

is proved under the proposed controller. Simulations

results show that the proposed control strategy is able

to regulate the DC-bus voltage and the power ﬂow

with good dynamic performances.

REFERENCES

Belhaouane, M., Saad, H., and Guillaud, X. (2014). Con-

trol and performance of modular multilevel converters

using resonant controller. Dallas. 40

Annual Confer-

ence on IEEE Industrial Electronics Society, IECON.

Chen, H., Xu, Z., and Zhang, F. (2006). Nonlinear con-

trol for vsc based hvdc system. Montreal, Que. IEEE,

Power Engineering Society General Meeting.

Chen, Y., Dai, J., Damm, G., and Lamnabhi-Lagarrigue, F.

(2013). Nonlinear control design for a multi-terminal

vsc-hvdc system. Zrich, Switzerland. European Con-

trol Conference (ECC).

Colbia-Vega, A., de Leon-Morales, J., Fridman, L., Salas-

Peaa, O., and Mata-Jim

enez, M. (2008). Robust exci-

tation control design using sliding-mode technique for

multimachine power systems. Electric Power Systems

Research, 78(9):1627 – 1634.

Dash, P., Routray, A., and Mishra, S. (1999). A neural net-

work based feedback linearising controller for hvdc

links. Electric Power Systems Research, 50(2):125 –

132.

Dierckxsens, C., Srivastava, K., Reza, M., Cole, S., Beerten,

J., and Belmans, R. (2012). A distributed dc voltage

control method for vsc mtdc systems. Electric Power

Systems Research, 82(1):54 – 58.

Jacobson, B. (2011). Abb power systems, developments in

multiterminal hvdc. IEEE EPEC, Winnipeg Manitoba.

Jammazi, C. (2008). Backstepping and partial asymptotic

stabilization: Applications to partial attitude control.

International Journal of Control, Automation, and

Systems, 6(6):1 – 14.

Jovic, D., Lamont, L., and Xu, L. (2003). Vsc transmis-

sion model for analytical studies. volume 3. IEEE,

Power Engineering Society General Meeting, Confer-

ence Proceeding.

Khalil, H. (2002). Nonlinear Systems. Prentice Hall, Upper

Saddle River, NJ 07458, 3rd. edition.

Kim, K. and Kim, Y. (2003). Robust backstepping control

for slew maneuver using nonlinear tracking function.

IEEE Trans. Control Syst. Technol., 11(6):822 – 829.

Moharana, A. and Dash, P. (2010). Input-output lineariza-

tion and robust sliding-mode controller for the vsc-

hvdc transmission link. IEEE Transactions on Power

Delivery, 25(3):1952 – 1961.

Moharana, A., Panigrahi, M., Panigrahi, B., and Dash, P.

(2006). Vsc based hvdc system for passive network

with fuzzy controller. pages 1 – 4, New Delhi. Inter-

national Conference on Power Electronics Drives and

Energy Systems PEDES.

Ramadan, H., Siguerdidjane, H., and Petit, M. (2008). Ro-

bust nonlinear control strategy for hvdc light transmis-

sion systems technology. pages 360 – 365, USA. 34

Annual Conference of the IEEE Industrial Electronics

Society IECON.

Ramadan, H. S., Siguerdidjane, H., Petit, M., and Kacz-

marek, R. (2012). Performance enhancement and ro-

bustness assessment of vsc-hvdc transmission systems

controllers under uncertainties. Electrical Power and

Energy Systems, 35:34 – 46.

Rashed, M., El-Anwar, M., and Youssef, F. (2008). Nonlin-

ear control scheme for vsc-hvdc transmission systems.

pages 468 – 491, Egypt. 34

Annual Conference of

the IEEE Industrial Electronics Society MEPCON.

Rault, P. (2014). Mod

elisation Dynamique et Commande

des R

eseaux

a Courant Continu Multi-Terminaux

Haute Tension. Th

ese de doctorat en genie electrique,

Doctorat delivr

e par l’ecole centrale de LILLE.

Reeve, J. and Sultan, M. (1994). Gain scheduling adaptive

control strategies for hvdc systems to accommodate

large disturbances. IEEE Transactions on Power Sys-

tems, 9(1):366 – 372.

Ruan, S., Li, G., Jiao, X., Sun, Y., and Lie, T. (2007).

Adaptive control design for vsc-hvdc systems based

on backstepping method. Electric Power Systems Re-

search, 77(5-6):559 – 565.

Sachdev, M., Fleming, R., and Chand, J. (1973). Op-

timal control of a hvdc transmission link. IEEE

Transactions on Power Apparatus and Systems, PAS-

92(6):1958 – 1965.

Setr

eus, J. and Bertling, L. (2008). Introduction to

hvdc technology for reliable electrical power systems.

pages 1 – 5, Sweden. PMAPS ’08 Proceedings of the

10th International Conference.

Skjetne, R. and Fossen, T. (2004). On integral control in

backstepping: Analysis of different techniques. vol-

ume 2, pages 1899 – 1904, Boston, Massachusetts.

American Control Conference.

Thomas, J., Poullain, S., and Benchaib, A. (2001). Analy-

sis of a robust dcbus voltage control system for a vsc

transmission scheme. pages 119 – 124, London UK.

Seventh International Conference on AC DC Power

Transmission.

Wang, G., Wai, R., and Liao, Y. (2013). Design of backstep-

ping power control for grid-side converter of voltage

source converter-based high-voltage dc wind power

generation system. IET Renewable Power Generation,

7(2):118 – 133.

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

602