
A Depth-based Approach for 3D Dynamic Gesture Recognition
Hajar Hiyadi
1,2
, Fakhreddine Ababsa
1
Christophe Montagne
1
, El Houssine Bouyakhf
2
and Fakhita Regragui
2
1
Evry Val d’Essonne University, Evry, France
2
Mohammed V University, Rabat, Morocco
Keywords:
3D Gesture Recognition, Gesture Tracking, Depth Image, Hidden Markov Models.
Abstract:
In this paper we propose a recognition technique of 3D dynamic gesture for human robot interaction (HRI)
based on depth information provided by Kinect sensor. The body is tracked using the skeleton algorithm pro-
vided by the Kinect SDK. The main idea of this work is to compute the angles of the upper body joints which
are active when executing gesture. The variation of these angles are used as inputs of Hidden Markov Models
(HMM) in order to recognize the dynamic gestures. Results demonstrate the robustness of our method against
environmental conditions such as illumination changes and scene complexity due to using depth information
only.
1 INTRODUCTION
1.1 Motivation
The goal of Human Robot Interaction (HRI) research
is to increase the performance of human robot inter-
action in order to make it similar to human-human
interaction, allowing robots to assist people in natural
human environments. As for communication between
humans, gestural communication is also widely used
in human robot interaction. Several approaches have
been developed over the last few years. Some ap-
proaches are based on data markers or gloves and use
mechanical or optical sensors attached to these de-
vices that transform flexion of the members into elec-
trical signals to determine the posture. These methods
are based on various informations such as the angles
and the joints of the hand which contain data position
and orientation. However, these approaches require
that the user wear a glove or a boring device with a
load of cables connected to the computer, which slows
the natural human robot interaction. In the other side,
computer vision is a non intrusive technology which
allows gesture recognition, without any interference
between the human and the robot. The vision-based
sensors include 2D and 3D sensors. However, ges-
ture recognition based on 2D images had some lim-
itations. Firstly, the images can not be in a consis-
tent level lighting. Second, the background elements
can make the recognition task more difficult. With the
emergence of Kinect (Zhang, 2012), depth capturing
in real time becomes very easy and allows us to obtain
not only the location information, but also the orien-
tation one. In this paper we aim to use only the depth
information to build a 3D gesture recognition system
for human robot interaction.
1.2 Related Work
A gesture recognition system includes several steps:
detection of one or more members of the human body,
tracking, gesture extraction and finally classification.
Hand tracking can be done based on skin color. This
can be accomplished by using color classification into
a color space. In (Rautaray and Agrawal, 2011), skin
color is used to extract the hand and then track the
center of the corresponding region. The extracted
surface into each chrominance space has an ellipti-
cal shape. Thus, taking into account this fact, the
authors proposed a skin color model called elliptical
contour. This work was extended in (Xu et al., 2011)
to detect and localize the head and hands. In addition,
the segmentation process is also an important step in
tracking. It consists of removing non-relevant objects
leaving behind only the regions of interest. Segmen-
tation methods based on clustering are widely used
in hand detection and especially K-means and expec-
tation maximization. In (Ghobadi et al., 2007) the
authors combine the advantages of both approaches
and propose a new robust technique named KEM (K-
103
Hiyadi H., Ababsa F., Montagne C., Bouyakhf E. and Regragui F..
A Depth-based Approach for 3D Dynamic Gesture Recognition.
DOI: 10.5220/0005545401030110
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 103-110
ISBN: 978-989-758-123-6
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

means Expectation Maximization). Other detection
methods based on 2D / 3D template matching were
also developed (Barczak and Dadgostar, 2005)(Chen
et al., 2008)(Xu et al., 2010). However, skin color
based approaches are greatly affected by illumination
changes and background scene complexity. There-
fore, recent studies tend to integrate new information
such as depth. Indeed, depth information given by
depth sensors can improve the performance of ges-
ture recognition systems. There are several stud-
ies that combine color and depth information, either
in tracking or segmentation (Bleiweiss and Werman,
2009)(Xia et al., 2011)(Qin et al., 2014)(Xu et al.,
2014). Other works combine depth information, color
and speech (Matuszek et al., 2014). In (Xia et al.,
2011), the authors use a silhouette shape based tech-
nique to segment the human body, then they combine
3D coordinates and motion to track the human in the
scene. Filtering approaches are also used in tracking
such as the Unscented Kalman Filter (Boesen et al.,
2011), the Extented Kalman Filter(F., 2009) and the
Prticle Filter(F. and Mallem, 2006). Other methods
are based on points of interest which have more con-
straints on the intensity function and are more reli-
able than the contour based approaches (Koller et al.,
2010). They are robust to occlusions present in a large
majority of images.
The most challenging problem in dynamic gesture
recognition is the spatial-temporal variability, when
the same gesture could be different in velocity, shape
and duration. These characteristics make recognition
of dynamic hand gestures very difficult compared to
static gestures (Wang et al., 2012). As in speech, hand
writing and character recognition (Saon and Chien,
2012)(Li et al., 2011), HMM were successfully used
in gesture recognition (Elmezain et al., 2008)(Eick-
eler et al., 1998)(Binh and Ejima, 2002). Actually,
HMM can model spatial-temporal time series and pre-
serve the spatial-temporal identity of gesture. The au-
thors in (Gu et al., 2012) developed a dynamic ges-
ture recognition system based on the roll, yaw and
pitch orientations of the left arm joints. Other mathe-
matical models such as Input-Output Hidden Markov
Model (IOHMM) (Bengio and Frasconi, 1996), Hid-
den Conditional Random Fields (HCRF) (Wang et al.,
2006) and Dynamic Time Warping (Corradini, 2001)
are also used to model and recognize sequences of
gestures.
In this paper, we propose a 3D dynamic gesture
recognition technique based on depth camera. The
basic framework of the technique is shown in Figure
1. The Skeleton algorithm given by the Kinect SDK
is used for body tracking. The 3D joints informations
are extracted and used to calculate new and more rel-
evant features which are the angles between joints.
Finally, discrete HMM with Left-Right Banded topol-
ogy are used to model and classify gestures. The eval-
uation experiments show the effectiveness of the pro-
posed technique. The performance of our technique
is further demonstrated with the validation step which
give good recognition even whithout training phase.
The rest of the paper is organized as follows: Section
2 describes our 3D dynamic gesture approach and the
features we used. Section 3 gives some experimen-
tal results. Finally, section 4 ends the paper with a
conclusion and futur work.
Figure 1: Flowchart of the proposed 3D dynamic gesture
recognition technique.
2 PROPOSED APPROACH
In the context of human robot interaction, the aim of
our work is to recognize five 3D dynamic gestures
based on depth information. We are interested in de-
ictic gestures. The five gestures we want to recognize
are: {come, recede, stop, pointing to the right and
pointing to the left }. Figure 2 shows the execution of
each gesture to be recognized. Our gesture recogni-
tion approach consists of two main parts: 1- Human
tracking and data extraction, and 2- gesture recogni-
tion.
2.1 Human Tracking and Data
Extraction
In order to proceed to the gesture recognition, we
need first to achieve a robust tracking for Human body
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
104

Figure 2: Five distinct gesture kind.
Figure 3: Kinect system coordinate.
and arms. Most recent tracking methods use color in-
formation. However, color is not a stable cue, and is
generally influenced by several factors such as bright-
ness changing and occlusions. Hence, color-based
tracking approaches fail often and don’t success to
provide 3D human postures at several times. In our
work we choose to use a depth sensor (Kinect) in or-
der to extract 3d reliable data. Figure 3 shows the ref-
erence coordinate frames associated to the acquisition
system.
The coordinates x, y and z denote, respectively, the
x and y positions and the depth value. Human track-
ing is performed using the Skeletal Tracking method
given by the kinect SDK
1
.This method projects a
skeleton on the human body image so each joint of
the body is related to a joint of the projected skeleton.
In this manner, it creates a collection of 20 joints to
each detected person. Figure 4 shows the information
used in our approach: depth image (b) and skeleton
tracking (c).
Figure 4: (a) RGB image, (b) depth image, (c) skeleton
tracking.
The mean idea of our approach is to estimate in
real time the variations of the active angles while ex-
1
http://msdn.microsoft.com/en-us/library/jj131025.aspx
ecuting the gestures. The considered angles are: α
elbow, β shoulder and γ armpit angle, as shown in
Figure 5. Each angle is then computed from the 3D
coordinates of the three joints that are commonly ac-
counted to it:
• α elbow angle is computed from the 3D coordi-
nates of elbow, wrist and shoulder joints.
• β shoulder angle is computed from the 3D co-
ordinates of shoulder, elbow and shoulder center
joints.
• γ armpit angle is computed from the 3D coordi-
nates of shoulder, elbow and hip joints.
Figure 5: α, β and γ angles.
When performing a gesture we record the values
given by each of these three angles and we store the
results in vectors as follow :
V
α
= [α
1
, α
2
, ..., α
T
] (1)
V
β
= [β
1
, β
2
, ..., β
T
] (2)
V
γ
= [γ
1
, γ
2
, ..., γ
T
] (3)
Where T is the length of the gesture sequence, it is
variable from a gesture to another and from a person
to another. The input vector of our 3D dynamic ges-
ture recognition system will be then written as:
V
α
= [α
1
, α
2
, ..., α
T
, β
1
, β
2
, ..., β
T
, γ
1
, γ
2
, ..., γ
T
] (4)
ADepth-basedApproachfor3DDynamicGestureRecognition
105
The gesture description based on angles variation
allows distinguishing between different human ges-
tures. Thus, for every canonical gesture, there is one
main angle which changes throughout the gesture and
the remaining two angles vary slightly. We consider
the five gestures defined previously. The angle which
is varing for come and recede is the angle α. Like-
wise, the angle γ for stop gesture, and angle β for both
pointing gestures. The main angle’s variations in each
gesture are showing in the Table 1.
Table 1: The main angle’s variations in each gesture (1, 2,
3, 4, 5 refer respestively to come, recede, pointing to right,
pointing to left, stop).
α β γ
1 180
◦
→ 30
◦
- -
2 30
◦
→ 180
◦
- -
3 - 90
◦
→ 150
◦
-
4 - 90
◦
→ 40
◦
-
5 - - 30
◦
→ 80
◦
In this work, we propose to use the sequences of
angles variations as an input of our gesture recogni-
tion system as explained in the next section.
2.2 Gesture Classification Method
Our recognition method is based on Hidden Markov
Models (HMM). HMM are widely used in temporal
pattern, speech, and handwriting recognition, they
generally yield good results. The problem in the
dynamic gestures is their spatial and temporal vari-
ability which make their recognition very difficult,
compared to the static gestures. In fact, the same
gesture can vary in speed, shape, length. However,
HMM have the ability to maintain the identity of
spatio-temporal gesture even if its speed and/or
duration change.
2.2.1 Hidden Markov Models
An HMM can be expressed as λ = (A, B, π) and de-
scribed by:
a) A set of N states S = {s
1
, s
2
, ..., s
n
}.
b) An initial probability distribution for each state Π
= {π
j
}, j = {1, 2, ..., N}, with π
j
= Prob(S
j
at t =
1).
c) A N-by-N transition matrix A = {a
i j
}, where a
i j
is the transition probability of s
i
to s
j
; 1 ≤ i, j ≤ N
and the sum of the entries in each row of the ma-
trix A must be equal to 1 because it corresponds to
the sum of the probabilities of making a transition
from a given state to each of the other states.
d) A set of observations O = {o
1
, o
2
, ..., o
t
}, t =
{1, 2, ..., T } where T is the length of the longest
gesture path.
e) A set of k discrete symbols V = {v
1
, v
2
, ..., v
k
}.
f) The N-by-M observation matrix B = {b
im
}, where
b
im
is the probability of generating the symbol v
k
from state s
j
and the sum of the entries in each row
of the matrix B must be 1 for the same previous
reason.
There are three main problems for HMM: eval-
uation, decoding, and training, which are solved
by using Forward algorithm, Viterbi algorithm, and
Baum-Welch algorithm, respectively (Lawrence,
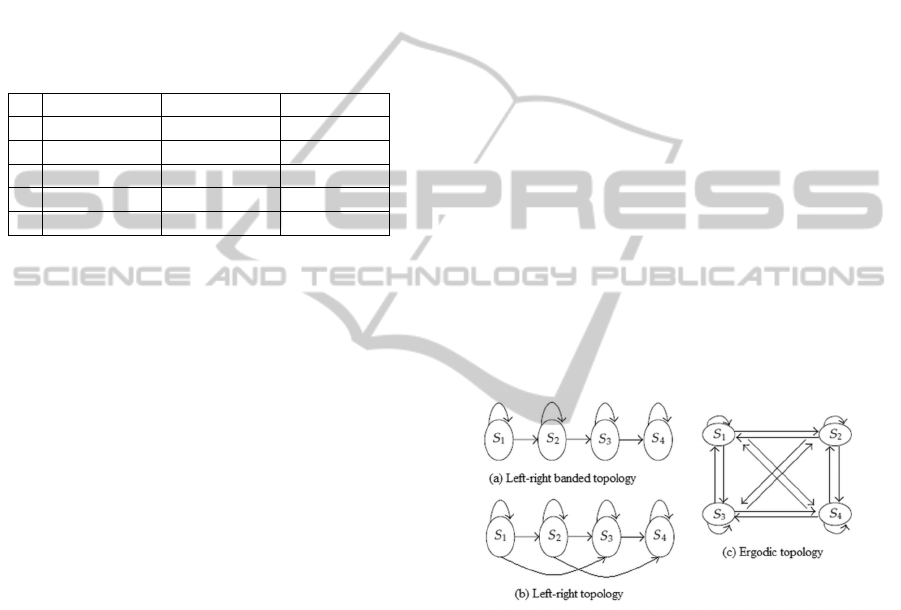
1989). Also, HMM has three topologies: Fully
Connected (Ergodic model) where each state can
be reached from any other state, Left-Right (LR)
model where each state can go back to itself or to
the following states and Left-Right Banded (LRB)
model in which each state can go back to itself
or the following state only (Figure 6). We choose
left-right banded model Figure 6(a) as the HMM
topology, because the left-right banded model is good
for modeling-order-constrained time-series whose
properties sequentially change over time. We realized
five HMM, one HMM for each gesture type.
Figure 6: HMM topologies.
2.2.2 Initializing Parameters for LRB Model
We created five HMM, one for each gesture. First of
all, every parameter of each HMM should be intial-
ized. We start with the number of states. In our case
this number is not the same for all the five HMM, it
depends on the complexity and duration of the ges-
ture. We use 12 states as maximum number and 8 as
minimum one in which the HMM initial vector pa-
rameters Π will be designed by;
Π = (1 0 0 0 0 0 0 0) (5)
To ensure that the HMM begins from the first state,
the first element of the vector must be 1. The second
parameter to be defined is the Matrix A which can be
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
106

written as:
A =
a
ii
1−a
ii
0 0 0 0 0 0
0 a
ii
1−a
ii
0 0 0 0 0
0 0 a
ii
1−a
ii
0 0 0 0
0 0 0 a
ii
1−a
ii
0 0 0
0 0 0 0 a
ii
1−a
ii
0 0
0 0 0 0 0 a
ii
1−a
ii
0
0 0 0 0 0 0 a
ii
1−a
ii
0 0 0 0 0 0 0 a
ii
(6)
where a
ii
is initialized by a random value. The
Matrix B is determinated by:
B = {b
im
} (7)
where b
im
is initialized by a random value.
2.2.3 Training and Evaluation
Our database is composed of 100 videos for each kind
gesture (50 for training and 50 for testing). In the
training phase the Baum-Welch algorithm (Lawrence,
1989) is used to do a full training for the initial-
ized HMM parameters λ = (Π, A, B). Our system is
trained on 50 sequences of discrete vector for each
kind of gesture by using LRB topology with the num-
ber of states ranging from 3 to 12. After the training
process, we obtain new HMM parameters (Π
0
, A
0
, B
0
)
for each type of gesture. According to the forward
algorithm with Viterbi path, the other 50 video se-
quences for each type of gesture are tested using the
new parameters. The forward algorithm computes
the probability of the discrete vector sequences for all
the five HMM models with different states. Thereby,
the gesture path is recognized corresponding to the
maximal likelihood of 5 gesture HMM models over
the best path that is determined by Viterbi algorithm.
The following steps demonstrate how the Viterbi al-
gorithm works on LRB topology (Elmezain et al.,
2009):
• Initialization:
for 1 ≤ i ≤ N,
δ
1
(i) = Π
i
· b
i
(o
1
)
φ
1
(i) = 0
• Recursion:
for 2 ≤ t ≤ T, 1 ≤ j ≤ N,
δ
t
(i) = max[δ
t−1
(i) · a
i j
] · b
j
(o
t
)
φ
t
(i) = argmax[δ
t−1
(i) · a
i j
]
• Termination:
p
∗
= max[δ
T
(i)]
q
∗
T
= argmax[δ
T
(i)]
• Reconstruction:
for T − 1 <= t <= 1
q
∗
t
= φ
t+1
(q
∗
t+1
)
The resulting trajectory (optimal states sequence) is
q
∗
1
, q
∗
2
, ..., q
∗
T
where a
i j
is the transition probability
from state s
i
to state s
j
, b
j
(o
t
) is the probability of
emitting o at time t in state s
j
, δ
t
( j) represents the
maximum value of s
j
at time t, φ
t
( j) is the index of
s
j
at time t and p
∗
is the state optimized likelihood
function.
3 EXPERIMENTAL RESULTS
3.1 Data Set
Our database is built with aroud 20 persons. Every-
one is invited to execute the five gestures that we have
defined before. Each gesture is executed 5 times per
person. So finally, we generated 500 sequences, 250
are used for training and 250 for testing. Each HMM
is trained with 50 gesture samples and tested with 50.
3.2 Experimental Protocol
Before the experiment, the experimental protocol was
given to the subjects which describes the begining and
the end of the five gestures. The gesture duration is
not fixed. The person can do a gesture whether slowly
or speedy. We used the Kinect sensor that must re-
main stable. The person must be in front of the kinect
and the distance must be heigher than 80 cm to well
detect the bodyl. The environment is sort of crowded
but no barrier should be between the person and the
camera to avoid losing tracking. During the gesture
the person should stay up.
The environment and the brightness do not affect
the data collection because we rely on depth only. A
given gesture is recognized corresponding to the max-
imal likelihood of five HMM models. So, if a new
executed gesture does not correspond to the five ges-
tures, it will be awarded to one of five classes corre-
sponding to the maximum probability and then rec-
ognized as one of them. To overcome this problem
we built a new database of 20 videos containing the
insignificant gestures when subject moves his hand
without any goal. The probabilities of belonging to
the five classes are very small. From here we deter-
mined a threshold for each class gesture. Thus, the
gesture is rejected if the maximum probability is less
than the threshold fixed for the corresponding gesture
class.
3.3 Recognition Results
Angles variations are plotted in Figure (7, 8, 9, 10 and
11). As it is showen, each gesture is characterized by
ADepth-basedApproachfor3DDynamicGestureRecognition
107

the most changing angle comapring to the two others.
We choose the state number of HMM for each gesture
according to the experiment results and find that the
recognition rate is maximum when the state number
is 11 states for the gestures come, recede and pointing
to the right, 12 for the gesture pointing to left, and 8
for the last gesture stop as shown in Figure 12. There-
fore, we use this setting in the following experiments.
A given gesture sequence is recognized in 0.1508 s.
The recognition results are listed in Table 2. We can
see that the proposed method can greatly improve the
recognition process, especially for opposed gestures
like come and recede, pointing to the right and point-
ing to left. We can also see that there is no confusing
between some gestures such as come and recede. In
this case, it is due to the fact that the angle α changes
during these two gestures decreases in come and in-
creases in recede. The same reasoning can be given
in the case of the tow opposed gestures, pointing to
the right and pointing to left. As a matter of fact, even
if the same angle varies in two different gestures, our
method can distinguish them.
Figure 7: Angles variations for come gesture.
Figure 8: Angles variations for recede gesture.
Table 3 presents a comparison of our approach
with that of the authors in (G. et al., 2012). They use
raw, roll and pitch orientations of elbow and shoul-
der joints of the left arm. Their database contains five
Figure 9: Angles variations for pointing to the right gesture.
Figure 10: Angles variations for pointing to the left gesture.
Figure 11: Angles variations for stop gesture.
gestures trained by one person and tested by two. The
gesture duration is fixed beforehand. In offline mode,
the accuracy of recognizing gestures executed by per-
sons who did training was found to be 85% with their
method and 97.2% with our method. And without
training, the recognition accuracy attained 73% with
their method and 82% with our method. The gestures
we have defined for the human robot interaction are
natural. They are almost the same that we use daily
and between people. Whereas, most methods in the
state of the art are based on constrained gestures that
use signs which are not natural. The proposed ges-
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
108

Figure 12: Recognition accuracy when changing the number of state of HMM from 3 to 14 states.
ture recognition approach is based only on depth in-
formation that is what makes it very robust against the
environment complexity and illumination variation.
Table 2: Confusing matrix and recognition accuracy.
1 2 3 4 5 Accuracy
1 50 0 0 0 0 100%
2 0 50 0 0 0 100%
3 0 0 49 0 1 98%
4 0 0 0 48 2 96%
5 1 0 0 3 46 92%
Average accuracy 97.2%
4 CONCLUSIONS AND FUTURE
WORKS
We described an efficient method for 3D natu-
ral and dynamic gesture recognition for human
robot/interaction. We have identified five deictic ges-
tures, which can be recognize using only depth in-
formation. The idea is to extract the 3D coordinates
of the joints of the upper part of the human body,
and then compute the angles corresponding to these
joints. These angles variation along the gestures are
used as inputs of Hidden Markov Models (HMM). We
propose one model for each gesture. The experimen-
tal results show that our approach gives better recog-
nition compared to the method in (G. et al., 2012).
Indeed, the recognition rate can reach up to 100%
for some kind of gestures. In addition, we give be-
low some characteristics of the proposed recognition
system. First, the training phase, it simply saves the
gesture when run. Second, the system can recognize
gestures even if the distance or the location of peo-
ple change. Third, although the speed of gestures can
Table 3: Comparison between the performance of our ap-
proach and Ye and Ha(G. et al., 2012)’s approach.
Methods Ye and Ha Our
(G. et al., 2012) approach
Gesture Dynamic Dynamic
nature
Used Raw, roll Angles
Info. and pitch between
orientations joints
of joints
Gestures 5 5
number
Joints 2 5
number
Used Segmented Brute
data
Classification HMM HMM
Training 75 500
database
People 2 21
for test
Gesture Fixed Variable
duration
Accuracy 73% 97.2%
vary from one person to another, the system is able to
recognize the gesture. Finally, the change in the dura-
tion of a gesture from one person to another does not
affect the recognition. In the future work, we will ex-
pand our gesture database in order to recognize differ-
ent gestures in the same sequence, we will also com-
bine the depth information with speech to make au-
tomatic the detection of the beginning and the end of
the gesture and make the complex gesture recognition
more robust.
ADepth-basedApproachfor3DDynamicGestureRecognition
109

REFERENCES
Barczak, A. and Dadgostar, F. (2005). Real-time hand track-
ing using a set of cooperative classifiers based on haar-
like features. In Research Letters in the Information
and Mathematical Sciences.
Bengio, Y. and Frasconi, P. (1996). Ieee transactions on
neural networks. In Input-output HMMs for sequence
processing.
Binh, N. D. and Ejima, T. (2002). Real-time hand gesture
recognition using pseudo 3-d hidden markov model.
In Proceedings of the 5th IEEE International Confer-
ence on Cognitive Informatics (ICCI ’06).
Bleiweiss, A. and Werman, M. (2009). Fusion time-of- ight
depth and color for realtime segmentation and track-
ing. In DAGM Symposium for Pattern Recognition.
Boesen, A., Larsen, L., Hauberg, S., , and Pedersen, K. S.
(2011). Unscented kalman filtering for articulated
human tracking. In 17th Scandinavian Conference,
SCIA.
Chen, Q., Georganas, N., and Petriu, E. (2008). Hand ges-
ture recognition using haar-like features and a stochas-
tic context-free grammar. In IEEE Transactions on
Instrumentation and Measurement.
Corradini, A. (2001). Dynamic time warping for off-line
recognition of a small gesture vocabulary. In ICCV
Workshop on RecognitionAnalysis, and Tracking of
Faces and Gestures in Real-Time Systems.
Eickeler, S., Kosmala, A., and Rigoll, G. (1998). Hidden
markov model based continuous online gesture recog-
nition. In Proceedings of 14th International Confer-
ence on Pattern Recognition.
Elmezain, M., Al-Hamadi, A., Appenrodt, J., and
Michaelis, B. (2009). A hidden markov model-based
isolated and meaningful hand gesture recognition. In
Journal of WSCG.
Elmezain, M., Al-Hamadi, A., and B.Michaelis (2008).
Real-time capable system for handgesture recognition
using hidden markov models in stereo color image se-
quences. In Journal of WSCG.
F., A. (2009). Robust extended kalman filtering for camera
pose tracking using 2d to 3d lines correspondences.
In International Conference on Advanced Intelligent
Mechatronics.
F., A. and Mallem, M. (2006). Robust line tracking using
a particle filter for camera pose estimation. In Pro-
ceedings of the ACM Symposium on Virtual Reality
Software and Technology.
G., Y., D., H., O., Y., and Weihua, S. (2012). Human gesture
recognition through a kinect sensor. In Robotics and
Biomimetics (ROBIO).
Ghobadi, S., Leopprich, O., Hartmann, K., and Loffeld, O.
(2007). Hand segmentation using 2d/3d images. In
Proceeding of image and Vision Computiong.
Gu, Y., Do, H., and Sheng, Y. O. W. (2012). Human gesture
recognition through a kinect sensor. In International
Conference on Robotics and Biomimetics.
Koller, D., Thrun, S., PlagemannVarun, C., and Ganapathi,
V. (2010). Real time identification and localization of
body parts from depth images. In IEEE International
Conference on Robotics and Automation (ICRA).
Lawrence, R. (1989). A tutorial on hidden markov mod-
els and selected applications in speech recognition. In
Proceeding of the IEEE.
Li, M., Cattani, C., and Chen, S. (2011). Viewing sea
level by a one-dimensional random function with long
memory. In Mathematical Problems in Engineering.
Matuszek, C., Bo, L., Zettlemoyer, L., and Fox, D. (2014).
Learning from unscripted deictic gesture and language
for human-robot interactions. In I. J. Robotic.
Qin, S., Zhu, X., Yang, Y., and Jiang, Y. (2014). Real-
time hand gesture recognition from depth images us-
ing convex shape decomposition method. In Journal
of Signal Processing Systems.
Rautaray, S. S. and Agrawal, A. (2011). A real time hand
tracking system for interactive applications. In Inter-
national journal of computer Applications.
Saon, G. and Chien, J. T. (2012). Bayesian sensing hid-
den markov models. In IEEE Transactions on Audio,
Speech, and Language Processing.
Wang, S., Quattoni, A., Morency, L., Demirdjian, D., and
Darrell, T. (2006). Hidden conditional random fields
for gesture recognition. In IEEE Computer Society
Conference on Computer Vision and Pattern Recogni-
tion (CVPR).
Wang, X., Xia, M., Cai, H., Gao, Y., and Cattani, C. (2012).
Hidden-markov-models-based dynamic hand gesture
recognition. In Mathematical Problems in Engineer-
ing.
Xia, L., Chen, C.-C., and Aggarwal, J. (2011). Human de-
tection using depth information by kinect. In Com-
puter Society Conference on Computer Vision and
Pattern Recognition - CVPR.
Xu, D., Chen, Y.-L., Wu, X., and Xu, Y. (2011). Integrated
approach of skincolor detection and depth information
for hand and face localization. In IEEE International
Conference on Robotics and Biomimetics - ROBIO.
Xu, D., Wu, X., Chen, Y., and Xu, Y. (2014). Online dy-
namic gesture recognition for human robot interac-
tion. In IEEE Journal of Intelligent and Robotic Sys-
tems.
Xu, J., Wu, Y., and Katsaggelos, A. (2010). Part-based ini-
tialization for hand tracking. In The 17th IEEE Inter-
national Conference on Image Processing (ICIP).
Zhang, Z. (2012). Microsoft kinect sensor and its effect. In
Multi Media.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
110
