
Modelling and Optimization of Strictly Hierarchical Manpower System
Andrej
ˇ
Skraba
1
, Eugene Semenkin
2
, Davorin Kofjaˇc
1
, Maria Semenkina
2
, Anja
ˇ
Znidarˇsiˇc
1
Matjaˇz Maletiˇc
1
, Shakhnaz Akhmedova
2
,
ˇ
Crtomir Rozman
3
and Vladimir Stanovov
2
1
Cybernetics & Decision Support Systems Laboratory, University of Maribor
Faculty of Organizational Sciences, Kidriˇceva cesta 55a, SI−4000 Kranj, Slovenia
2
Siberian State Aerospace University, ”Krasnoyarsky rabochy” av. 31, Krasnoyarsk, 660014, Russia
3
Faculty of Agriculture and Life Sciences, University of Maribor, Pivola 10, SI 2311 Hoˇce, Slovenia
Keywords:
Manpower, Supply Chain, Optimization, System Dynamics, Genetic Algorithms, Optimal Control.
Abstract:
This paper addresses the problem of the hierarchical manpower system control in the restructuring process.
The restructuring case study is described where eight topmost ranks are considered. The desired and actual
structure of the system is given by the actual numbers of men in a particular rank. The system was modelled
in the dicrete state space with state elements and flows representing the recruitment, wastages and retirements.
The key issues were identified in the process as the stating of the criteria function, which are time variant
boundaries on the parameter values, the chain stucture of the system and the tendency for the system to os-
cilate at given initial conditions. The oscillatory case is presented and the dynamic programming approach
was considered in the optimization as unsuitable, examining the oscillations. The boundary space and optimal
solution space were considered by indicating the small area where the solution could be optimal. The aug-
mented finite automaton was defined which was used in the optimization with the adaptive genetic algorithm.
The developed optimization method enabled us to successfully determine proper restructuring strategy for the
defined manpower system.
1 INTRODUCTION
Strictly hierarchical manpower systems can be found
in many places in production, industry, the public sec-
tor and the army, for example. As a case study we will
consider the Slovenian Army, which has recenty been
under the restructuring process, where the number of
officers in the eight topmost ranks, from Second Lieu-
tenant to Major General had to be changed according
to
NATO
standards (
ˇ
Skulj et al., 2008;
ˇ
Skraba et al.,
2011;
ˇ
Skraba et al., 2015). This mean that, for exam-
ple, the nuber of men in the rank of Second Leutenant
had to be reduced from 256 down to 148; for the case
of Lieutenant, the number of men should be increased
from 258 to 289 etc. The restructuring process for the
eight topmost ranks is best described by the Figure 1.
On the x-axis of Figure 1, the eight ranks are marked
as x
1
. . . x
8
while the number of men is shown on the
x-axis. The desired values are shown by the dashed
rectangles while the actual values are shown by solid
lines. The optimal control of a large manpower sys-
tem is a challenging task (
ˇ
Skraba et al., 2011;
ˇ
Skraba
et al., 2015) due to the time variant boundaries of key
parameters, that determine the system (Smith, 1998;
Huang et al., 2009; Kofjaˇc et al., 2009). There have
been many atempts to provide the optimal solution
of the descibed problem such as discrete minimiza-
tion of quadratic performanceindex (Mehlman, 1980)
however, there is no proper solution provided (Taran-
tilis, 2008), which would consider the fact, that the
boundaries on the particular parameters might change
in time. For example, the recruitment policy might
be changed during the years of restructuring and the
boundaries for the recruitment parameters change ac-
cordingly. Main goal is to formulate the mathemat-
ical model of manpower system and to develop al-
gorithms, that will provide consistent, nonoscilatory
control strategies to bring the strict hierarchical man-
power system from initial states to desired end states
(Mehlman, 1980;
ˇ
Skraba et al., 2011;
ˇ
Skraba et al.,
2015). Since the addressed problem resembles the
supply chain, similar approaches could be applied
in e.g. inventory control, where oscillations are not
desired or in processing industry control where the
stability of the levels in chained tanks is important
(Schwartz et al., 2006).
215
Škraba A., Semenkin E., Kofjac D., Semenkina M., Znidaršic A., Maletic M., Akhmedova S., Rozman C. and Stanovov V..
Modelling and Optimization of Strictly Hierarchical Manpower System.
DOI: 10.5220/0005546002150222
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 215-222
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: The desired (dashed rectangle) and actual (solid
rectangle) values in a particular rank. It can be observed,
that in the first rank x
1
, the numbers should be reduced, in
x
2
increased, in x
3
reduced etc. This makes the control of
the chain more challenging. The initial transition process is
prone to oscillations.
2 MODELLING OF THE
MANPOWER SYSTEM
The system described could be modelled as the cas-
caded exponential delay structure with the ouflow in
each compartment as shown in Figure 2. Our ap-
proach differs from the well applied Markov chain
methodology (Guerry, 2014; Dimitriou and Tsantasb,
2010; Lanzarone et al., 2010) in modelling approach,
where System Dynamics (Forrester, 1973) has been
applied. In this manner, the model could be easily un-
derstood, which is important for the end users. If the
end user does not understand the model behind the so-
lution it is difficult to expect, that the system will be
properly applied. The input to the system in Figure
2 is represented by u(k) where k represents the dis-
crete time step k = 0, 1, . . . . In our case, this is the
recruitment and it is the only possible input since one
could reach the topmost rank only in strict hierarchi-
cal order, from the bottom up. It is not possible, for
example, to enter the rank of Major not being the Cap-
tain first. The modelling of the system is similar to the
u(k)
−−−−→
x
1
R(x
1
,r
1
)
−−−−→ x
2
R(x
2
,r
2
)
−−−−→ ··· x
n
R(x
n
,r
n
)
−−−−→
y
F(x
1
, f
1
)
y
F(x
2
, f
2
)
y
F(x
n
, f
n
)
Figure 2: Cascaded Exponential Delay Structure of Man-
power System.
modelling of supply chains (Kok et al., 2005; Pastor
and Olivella, 2008; Huang et al., 2009; Chattopad-
hyay and Gupta, 2007; Feyter, 2007; Guo et al., 1999;
Kanduˇc and Rodiˇc, 2015) where similar undesired ef-
fects occur, such as bullwhip (Kok et al., 2005). Here
we consider eight ranks x
1
, . . . , x
8
, which are shown
in Figure 2. The promotions are marked with R and
are dependant on the value of the state element x
n
as
well as on the promotion parameter value r
n
. The
wastages are marked with F
n
and are also dependent
on the value of the state element x
n
and the value of
the fluctuation coefficient f
n
. The presented structure
is a delay chain where the change in the first element
propagates through the whole chain. This represents
a certain difficulty in providing proper system control
(Aickelin et al., 2004; Bard et al., 2007; Albores and
Duncan, 2008). The system shown in Figure 2 could
be expressed by the principles of System Dynamics
(Forrester, 1973) as a the set of difference equations
in discrete form:
x(k) = x(k
0
) +
k−1
∑
i=k
0
(R
in
(i) −R
out
(i)) ∆t (1)
∆x(i)
∆t
= R
in
(i) −R
out
(i) (2)
where Eq. 2 represents net change of state x. Stock
variables x
1
, x
2
, . . . , x
n
(Levels) represent the state of
the system, in our case the number of officers in a
particular rank x
1
, x
2
, . . . , x
n
, while the Rate variables
R and F (both are rates) represent the change in stocks
such as transition rates R and fluctuation rates F de-
fined as:
• R
0
rate element which represents the input to the
system, i.e. recruiting, determined by value u.
• R
1
rate element which represents transitions from
rank x
1
to rank x
2
. R
1
is determined by the value
of x
1
and coefficient r
1
.
• R
2
rate element which represents transitions from
rank x
2
to rank x
3
. R
2
is determined by the value
of x
2
and coefficient r
2
, etc.
• F
1
rate element which represents the fluctuation
from rank x
1
. F
1
is determined by the value of x
1
and coefficient f
1
.
• F
2
rate element which represents the fluctuation
from rank x
2
. F
2
is determined by the value of x
2
and coefficient f
2
, etc.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
216
In matrix form the system shown in Fig. 2 in discrete
space where ∆t = 1, takes the form of:
(
x(k+ 1) = Ax(k) + Bu(k)
y(k) = Cx(k) + Du(k)
(3)
where matrix A is the matrix of coefficients. The in-
put u(k) to the considered system is provided by ma-
trix B to x
1
such that
x
1
(k+ 1) = [1−r
1
(k) − f
1
(k)] x
1
(k) + u(k) (4)
In our case u(k) represents the new recruitment to
rank x
1
which is the input of the system. The dy-
namics of the model depends on recruitment, pro-
motions and the fluctuation coefficients. Coefficient
values r(k), f(k) and the input u(k) are determined
with regard to the historical data, approximately for
the past decade. The model was developed with
MATLAB/Simulink
(
ˇ
Skraba et al., 2011;
ˇ
Skraba et al.,
2015). The task to achieve the desired number of men
in particular rank is expressed as the distance to the
target function which is predefined as the function
with exponential term (
ˇ
Skraba et al., 2011); this dis-
tance should be minimized:
J =
r
∑
n=1
t
k
∑
i=0
z
n
(i) −x
n
(i)
2
=
t
k
∑
i=0
z(i) −x(i)
2
, (5)
z
n
(i) is the target function value for rank n at step
i. One should compute min
u∈U,r∈R, f∈F
J where U,
R and F are input parameters with predefined value
boundaries. The deviation from the desired values is
only one part of the problem definition. As we will
see this is not sufficient since there is a possibility
that oscillations in the gained strategy might occur.
Let us consider the example of three ranks, x
1
, x
2
, x
3
with initial conditions x
1
(0), x
2
(0), x
3
(0) and target
values z(k) with boundaries:
LB
u
≤ u(k) ≤ UB
u
LB
r
≤ r(k) ≤ UB
r
LB
f
≤ f(k) ≤ UB
f
(6)
At each time-step the optimization problem is solved
for ψ(k+ 1):
min
u,r, f
[z
1
(k) −x
1
(k) + f
1
(k)x
1
(k) −u(k)+
x
1
(k)r
1
(k)]
2
+ [z
2
(k) −x
2
(k) + f
2
(k)x
2
(k)−
x
1
(k)r
1
(k) + x
2
(k)r
2
(k)]
2
+ [z
3
(k) −x
3
(k)+
f
3
(k)x
3
(k) −x
2
(k)r
2
(k) + x
3
(k)r
3
(k)]
2
If we perform the optimization by the proposed equa-
tion the solutions might exercise undesired oscilla-
tions. Since there is no weight put on the oscillations
in the rate elements, this is possible however unde-
sired. For example, if the recruitment oscillated, it
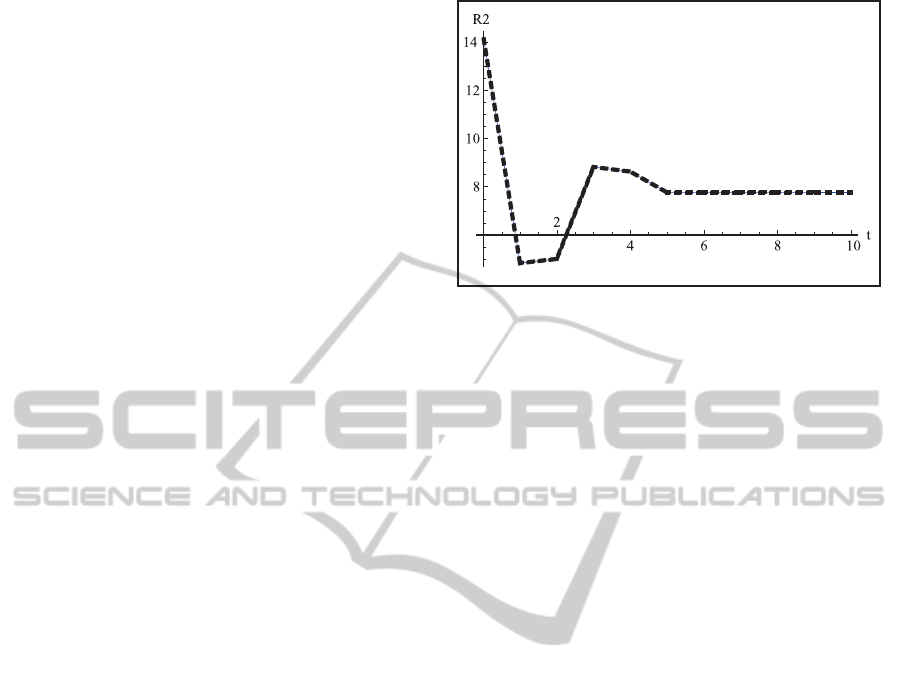
Figure 3: Example of the oscillating promotions on the Rate
element R
2
.
would mean that one should adjust the capacity of the
training facilities accordingly which would not be de-
sired. Here one strives to get the solution in the form
of a moderate policy for all variables in question. An
example of such a solution, which is optimal if only
the distance from the desired trajectory is considered,
is shown in Figure 3. In the Figure 3 the oscilla-
tions for the promotion from the Second Lieutenant
to Lieutenant is shown. An important limitation that
should be considered when stating the optimization
problem is sensitivity to upper and lower boundaries.
If one considers only one state element with a con-
stant input for the recruitment and variable output rate
coefficient, the feasability of achieving the target val-
ues is illustrated in Figure 4. On the x-axis the Lower
Boundary (LB) value is shown going from 0 to 1, sim-
ilarly for the x-axis where the Upper Boundary (UB)
is shown. On the z axis the Difference between the de-
sired and actual value is shown. Although this is only
an example, the real numbers are much higher and
such a strategy would not be acceptable. One could
observe the unfeasible region in the x-y plane due to
the lower and upper boundaries. It is interesting that
for the simplest case the optimal region in the upper
part of Figure 4 is relatively small. In this case we
actually examine the lower and upper boundary space
and observe the optimality region. As can be observed
the volume is not symmetrical leading to the possibil-
ity of searching in the direction of the lowest devia-
tion from the desired trajectory. Therefore, in order
to prevent the system from this oscillating behaviour,
the automaton A
2
has been constructed which consid-
ers strategies with one extremum point where:
• The set of states is S = {S
0
, S
1
, S
2
, S
3
, S
4
, S
5
}
• The comparison alphabet is A = {l, e, g}
• The initial state is i = S
0
• The set of terminal states is T = {S
0
, S
1
, S
2
, S
3
, S
4
}
ModellingandOptimizationofStrictlyHierarchicalManpowerSystem
217

Figure 4: Feasibility region for the system with one state.
Here only the variation of the output rate element is con-
sidered. Half of the x-y plane is not feasible. The optimal
region is shown only as a small part of the parameter bound-
ary space.
• The set of probabilities in the optimization penalty
function P = {p
0
, p
1
, p
2
, p
3
, p
4
}
The transition function of A
2
, δ : S×A → S is defined
by the rules A:
p l e g
↔ S
0
p
0
S
2
S
0
S
1
← S
1
p
0
S
3
S
1
S
1
← S
2
p
0
S
2
S
2
S
4
← S
3
p
1
S
3
S
3
S
5
← S
4
p
2
S
5
S
4
S
4
← S
5
p
3
S
5
S
5
S
5
(7)
An important addition is the augmenting of the au-
tomaton with the probability operator p which is ap-
plied at the optimization as the penalty coefficient. In
our case we can restate the criteria function as:
Ψ
J
= min
u,r, f
A (p)
h
r, f,
t
k
∑
k=1
z(k) −x(k)
T
W
z(k) −x(k)
i
(8)
subject to:
u
min
(k) ≤ u(k) ≤ u
max
(k)
r
min
(k) ≤ r(k) ≤ r
max
(k)
f
min
(k) ≤ f(k) ≤ f
max
(k)
(9)
where A (p) represents the applied automaton with
the augmented penalty probability, which alters the
optimization function when the terminal state is not
acceptable by appropriate weight, eliminating im-
proper strategies. This is applied to the evolution-
ary algorithm and alters the value of the minimization
function when the terminal state is not acceptable ac-
cording to the appropriate weight. The automaton is
also defined by the penalty coefficients p
0
, p
1
, p
2
and
p
3
according to the number of alternating steps that
were exercised by a particular strategy.
3 ADAPTIVE EVOLUTIONARY
ALGORITHM WITH
CONSTRAINT HANDLING
METHODS
A penalty method was developed in order to reject
the infeasible solutions which exercise oscillations of
input parameters, such as r(k) and f(k). Here, os-
cillations on the rate elements are also not desired.
The idea behind the developed penalty method is that
the discrete derivative of each r and f can be used to
see if this function changed its orientation, i.e. the
function is non-monotonic. After evaluating the er-
ror in the genetic algorithm, the feasibility is checked
at each step of the algorithm. In order to calculate
the penalty function, we have calculated the number
of times when the derivative was more than or equal
to zero, and the number of times when it was less
than zero. For each case we have also calculated the
sum of the derivative values for positive and negative
points separately. The derivative value for the input to
the system u was normalized to the interval [0,1], as
its value is much bigger than for the rest of variables
since recruitment is an absolute value and all other pa-
rameters are considered as coefficients between 0 and
1. In the next step, the two conditions were checked.
Firstly, we have checked if all of the derivative values
are positive or negative. In this case, the penalty value
for this time series is zero. If there were several posi-
tive and several negative values, than the penalty size
was set to the smallest module value between the two
sums of positive and negative derivatives respectively.
The penalty calculation can be formalized as (
ˇ
Skraba
et al., 2015):
penalty =
0, if (N
p
= T −1orN
n
= T −1),
|S
n
|, i f S
p
< S
n
,
|S
p
|, if S
n
< S
p
,
(10)
where N
p
and N
n
are the numbers of positive and neg-
ative derivative values, and S
p
and S
n
are the sums
of the positive and negative derivative values respec-
tively. These heuristic penalty values are calculated
based on the idea that if most of the time the deriva-
tive was higher than zero, than the negative values
should be changed to positive ones, so that these time
series would become feasible. The oposite action is
needed if the derivative is negative. The overall mod-
ified penalty value for all the time series was Total
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
218

Penalty (TP) and used in the genetic algorithm as:
TP = C ·
k−1
∑
i=0
pnlty
r
+
k
∑
i=0
pnlty
f
+ pnlty
u
!
·
√
G,
(11)
where C is a penalty weight constant and G is the cur-
rent generation number. In this case the penalty size
increases at each generation. We also used a modifica-
tion of the finite automaton defined as the set of rules
(7) as a constraint handling method, and its main idea
was that if the system ends up in states S
3
, S
4
or S
5
, it
means that the correspondingcoefficient made at least
one oscillation, which is not desirable. In this case
the finite automaton returned penalty value showing
that this time series is not desirable and formed the
penalty function. The return value is shown as the p
i
value, defined by the equation:
pnlty =
0, if p
0
,
c
i+1
−c
i
, if p
1
,
c
i
−c
i+1
, if p
3
,
|c
i+1
−c
i
|+ penalty
i−1
, if p
3
,
(12)
where c
i
is the coefficient value for the state element
i, and penalty
i−1
is the penalty value for the previous
state. The return value is zero in states S
0
, S
1
and S
3
.
For states S
3
and S
4
the return value depends on the
size of the oscillation tracked, and for the final state
S
5
the return value was the sum of the current and
previous penalty during the oscillations of the time
series.
4 RESULTS
Figure 5 shows the example of the nonoscilatory dy-
namics on the state element for Second Lieutenant
(Level element L). On the x-axis the time in years
is shown. Here we consider a six year period. On the
y-axis the nunber of men in the rank of Second Leu-
tainant is shown. In this case, we have considered the
0 1 2 3 4 5 6
40
50
60
70
80
90
100
Time [year]
L [men]
Figure 5: Example of the nonoscillatory dynamics on the
state element for Second Lieutenant (Level element L).
reduction of the number of men from 100 to 70. It can
be observed that the state element does not cause os-
cillations due to the applied modified finite automaton
at the optimization process. Advanced optimization
approaches have been descibed in (Semenkin and Se-
menkina, 2012b; Semenkin and Semenkina, 2012c;
Semenkin and Semenkina, 2012a; Semenkin and Se-
menkina, 2014) with modified finite automaton (FA)
(
ˇ
Skraba et al., 2014). Figure 6 shows the example
of the nonoscillatory dynamics of the promotions on
the Rate element R. Again, on the x-axis the time for
the period of six years is shown. This time, on the
y-axis, the rate of promotions is shown. The unit on
the y-axis can be noticed which is [men/year]. As one
can observe, for the case of three flows, there are no
oscillations in the strategy. The system stabilizes at
time k = 5. Figure 7 shows the dynamics on the rate
elements of Fluctuations. As before, the x-axis repre-
sents time in years while the y-axis shows the rates
of fluctuations with the unit of men per year. The
oscillations are not present which fulfils our goal of
providing a nonoscillatory strategy to achieve the de-
sired states. All three elements, state, promotion rates
as well as fluctuation rates are nonoscillatory provid-
ing the moderate policy which would lead the sys-
0 1 2 3 4 5
0
2
4
6
8
10
12
14
16
Time [year]
R [men/year]
Figure 6: Example of the nonoscillatory dynamics of the
promotions on the Rate element R.
0 1 2 3 4 5
0
4
8
12
Time [year]
F [men/year]
Figure 7: Example of the nonoscillatory dynamics of the
fluctuations F.
ModellingandOptimizationofStrictlyHierarchicalManpowerSystem
219

tem from the initial states to the desired states in the
prescribed time. Although the change might not ap-
pear to be significant, it is obvious that the strategy
of the HQ could not examine oscillations since there
are many activities bond to one another. Besides, that
the undesired disturbances could propagate within the
whole system.
5 CONCLUSION
The determinatiion of the control strategy for the hi-
erarchical manpower system is demanding task due
to the chain structure of the considered system. The
system was sucessfully described in the discrete state
space. Another important difficulty is time variant
boundaries on the parameter values. The bound-
aries are also dependant on the state elements and
therefore also change in time. All the mentioned
conditions put the described problem in the field of
hard problems
. An additional condition is that os-
cillations in any of the parameters or states are not
desirable. The approach with the classical dynamical
programming proved that oscillations are inevitable if
one only seeks the shortest time to achieve the stated
goals. By the consideration of the lower and upper
boundaries for the one state example, we have shown
that the optimal region for a particular parameter is
limited and dependent on the values of the lower and
upper boundaries. Oscillations were sucessfully ter-
minated by the application of the modified finite au-
tomaton which also considers the penalty function for
the parameter discrete derivatives. The applied adap-
tive genetic algorithm has been tested and provides
promising results for solving such complex tasks. An
important issue which was not addressed in the paper
is the user interface since the user has to deal with ap-
proximately 100 variables for controlling only eight
ranks in the period of 10 years. The develpedmethod-
ology is applicable for controlling not only the man-
power systems but also similar supply chain struc-
tures where one has to deal with the bullhip effect
(Kok et al., 2005). A general observation of the lit-
erature review showed that there is no single method
that would provide an optimum solution for the de-
scribed problem. One reason lies in the weights that
could be arbitrarily applied to a particular part of the
optimization problem.
Initially it would seem reasonable to define the
control problem only as minimization of the distance
to the target function with consideration of parameter
boundaries. Here the rationale is that the target trajec-
tory should be reached without considering the costs
when rate elements are within those prescribed, i.e.
normal boundaries. This kind of problem formula-
tion would actually yield the optimum solution if one
would like to achieve target values in the shortest pos-
sible time. An important finding is however the state-
ment of the problem, where only the minimization of
the distance to the target function by considering the
boundaries is insufficient, resulting in possible unde-
sired oscillatory solutions.
An important reduction of the complexity of the
problem addressed was achieved by introducing the
Trajectory function.
In order to complete the definition of the control
problem, the acceptable strategies were described and
FA were developed accordingly. The differences be-
tween two differently stated control problems were
shown in examples. The application of FA provided
proper results where the gained strategies did not dis-
play undesired oscillation patterns. Certainly, there is
a cost that is paid for providing the proper shape of the
strategy, which was shown by the different values of
quadratic performance index, meaning that more time
is needed to achieve the desired goal.
With the application of the developed system
decision-makers were faced with considerable gaps
between desired and estimated states, which were
indicated by the results of the described scenarios.
Experts and decision-makers were certainly roughly
aware of these discrepancies, but the results provided
by the developed system offered much more explicit
and elaborated evidence of the problems related to fu-
ture trends.
The provided real world example and solution
showed that the developed approach successfully pro-
vides the strategies which could be implemented in
the real-world system. According to the stated scenar-
ios an important question concerning the attainability
of a particular rank has been answered.
An important consideration in the application of
optimization techniques is user interaction. Opti-
mization methods applied are advanced, yet the sys-
tem should enable user-friendly manipulation of input
variables. It has to be mentioned that the user inter-
face has a major role in the addressed optimization
problem. Users try to optimize the process regardless,
of advanced analytical and numerical techniques with
their knowledge about the system and previous expe-
rience. A useful user interface could solve a signif-
icant portion of the problem by a simple calculation
which is usually carried out ad hoc. The entire sys-
tem for manpower planning was developed as major
changes in the military system were made which had
not been previously faced. Drastic changes in rank
numbers yielded a new dimension to the problem of
the manpower planning of officers who had to be sup-
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
220

ported by the new approach described here. However,
no sophisticated numerical procedure could be suc-
cessful without: a) a user friendly interface, and b) an
understanding of the problem by the user. In our case,
the target functions as well as the parameter bound-
ary values are stated as time vectors. In the worst
case, the user has to determine 43 vectors; 1 vector of
initial states, 34 boundary vectors and 8 vectors with
target trajectories in order to perform a particular op-
timization run. The minimal set of input data when
boundaries and initial states are set automatically on
the basis of historical data is the vector of goal states
with terminal time.
ACKNOWLEDGEMENT
This research is financed by Slovenian Research
Agency ARRS, Proj. No.: BI-RU/14-15-047 and Re-
search Program Group No. P5-0018 (A).
REFERENCES
Aickelin, U., Dowsland, U., and Kathryn, A. (2004). An in-
direct genetic algorithm for a nurse-scheduling prob-
lem. Comput. Oper. Res., 31(5):761–778.
Albores, P. and Duncan, S. (2008). Government prepared-
ness: Using simulation to prepare for a terrorist attack.
Comput. Oper. Res., 35(6):1924–1943.
Bard, J. F., Morton, D., and Wang, Y. (2007). Workforce
planning at USPS mail processing and distribution
centers using stochastic optimization. Ann. Oper. Res.,
2007(155):51–78.
Chattopadhyay, A. K. and Gupta, A. (2007). A stochastic
manpower planning model under varying class sizes.
Ann. Oper. Res., 2007(155):41–49.
Dimitriou, V. A. and Tsantasb, N. (2010). Evolution of a
time dependent markov model for training and recruit-
ment decisions in manpower planning. Linear Algebra
and its Applications, 433(11-12):1950–1972.
Feyter, T. D. (2007). Modeling mixed push and pull pro-
motion flows in manpower planning. Ann. Oper. Res.,
2007(155):25–39.
Forrester, J. (1973). Industrial Dynamics. MIT Press, Cam-
bridge, MA.
Guerry, M.-A. (2014). Some results on the embeddable
problem for discrete-time markov models in man-
power planning. Communications in Statistics - The-
ory and Methods, 43(7):1575–1584.
Guo, Y., Pan, D., and Zheng, L. (1999). Modeling mixed
push and pull promotion flow. Ann. Oper. Res.,
1999(87):191–198.
Huang, H.-C., Lee, L.-H., Song, H., and Thomas Eck, B.
(2009). Simman-a simulation model for workforce
capacity planning. Comput. Oper. Res., 36(8):2490–
2497.
Kanduˇc, T. and Rodiˇc, B. (2015). Optimization of a fur-
niture factory layout. Croatian Operational Research
Review, 6(1):121–130.
Kofjaˇc, D., Kljaji´c, M., and Rejec, V. (2009). The anticipa-
tive concept in warehouse optimization using simula-
tion in an uncertain environment. European Journal
of Operational Research, 193(3):660–669.
Kok, T., Janssen, F., Doremalen, J., Wachem, E., Clerkx,
M., and Peeters, W. (2005). Philips electronics syn-
chronizes its supply chain to end the bullwhip effect.
Interfaces, 35(1):37–48.
Lanzarone, E., Matta, A., and Scaccabarozzi, G. (2010).
A patient stochastic model to support human resource
planning in home care. Production Planning & Con-
trol, 21(1):3–25.
Mehlman, A. (1980). An approach to optimal recruitment
and transition strategies for manpower systems using
dynamic programming. Journal of Operational Re-
search Society, 31:1009–1015.
Pastor, R. and Olivella, J. (2008). Selecting and adapting
weekly work schedules with working time accounts:
A case of a retail clothing chain. European Journal of
Operational Research, 184:1–12.
Schwartz, J. D., Wang, W., and Rivera, D. E. (2006).
Simulation-based optimization of process control
policies for inventory management in supply chains.
Automatica, 42(8):1311–1320.
Semenkin, E. and Semenkina, M. (2012a). The choice
of spacecrafts’ control systems effective variants with
self-configuring genetic algorithm. In Informatics in
Control, Automation and Robotics: Proceedings of
the 9th International Conference ICINCO, pages 84–
93.
Semenkin, E. and Semenkina, M. (2012b). Self-configuring
genetic algorithm with modified uniform crossover
operator. In Tan, Y., Shi, Y., and Ji, Z., editors, Ad-
vances in Swarm Intelligence, volume 7331 of Lecture
Notes in Computer Science, pages 414–421. Springer
Berlin Heidelberg.
Semenkin, E. and Semenkina, M. (2012c). Self-
configuring genetic programming algorithm with
modified uniform crossover. In Proceedings of the
Congress on Evolutionary Computations of the IEEE
World Congress on Computational Intelligence (CEC
WCCI 2012), pages 1918–1923, Brisbane, Australia.
SCITEPRESS.
Semenkin, E. and Semenkina, M. (2014). Stochastic mod-
els and optimization algorithms for decision support
in spacecraft control systems preliminary design. In
Ferrier, J.-L., Bernard, A., Gusikhin, O., and Madani,
K., editors, Informatics in Control, Automation and
Robotics, volume 283 of Lecture Notes in Electri-
cal Engineering, pages 51–65. Springer International
Publishing.
ˇ
Skraba, A., Kofjaˇc, D.,
ˇ
Znidarˇsiˇc, A., Maletiˇc, M., Rozman,
ˇ
C., Semenkin, E. S., Semenkina, M. E., and Stanovov,
V. V. (2015). Application of self-gonfiguring genetic
algorithm for human resource management. ournal of
Siberian Federal University. Mathematics & Physics,
8(1):94–103.
ModellingandOptimizationofStrictlyHierarchicalManpowerSystem
221

Smith, J. (1998). The Book. The publishing company, Lon-
don, 2nd edition.
Tarantilis, C. (2008). Editorial: Topics in real-time sup-
ply chain management. Computers & Operations Re-
search, 2008(35):3393–3396.
ˇ
Skraba, A., Kljaji´c, M., Papler, P., Kofjaˇc, D., and Obed, M.
(2011). Determination of recruitment and transition
strategies. Kybernetes, 40(9/10):1503–1522.
ˇ
Skraba, A., Semenkin, E., Semenkina, M., Kofjaˇc, D.,
ˇ
Znidarˇsiˇc, A.,
ˇ
C. Rozman, Maletiˇc, M., Akhmedova,
S., and V.Stanovov (2014). Development of discrete
manpower model and determination of optimal con-
trol strategies. In Proceedings of the XVIII Inter-
national Scientific Conference Reshetnev Readings,
pages 421–423, Krasnoyarsk, Russia. SibSAU.
ˇ
Skulj, D., Vehovar, V., and
ˇ
Stamfelj, D. (2008). The
modelling of manpower by Markov chains - a case
study of the Slovenian armed forces. Informatica,
2008(32):289–291.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
222
