
Application of Sensory Body Schemas to Path Planning
for Micro Air Vehicles (MAVs)
Eniko T. Enikov
1
and Juan-Antonio Escareno
2
1
Department of Aerospace and Mechanical Engineering, University of Arizona,
1130 N. Mountain Ave, Tucson, AZ 85721, U.S.A.
2
Directorate for Research and Innovation (DRII), Institut Polytechnique des Sciences Avanc
´
ees (IPSA),
7-9 Rue Maurice Grandcoing, Ivry-sur-Seine, 94200, France
Keywords:
Micro-Air Vehicles, Artificial Neural Network, Path Planning, Body Schema, Cognitive Robotics.
Abstract:
To date, most autonomous micro air vehicles (MAV-s) operate in a controlled environment, where the location
of and attitude of the aircraft are measured be dedicated high-power computers with IR tracking capability. If
MAV-s are to ever exit the lab and carry out autonomous missions, their flight control systems needs to utilize
on-board sensors and high-efficiency attitude determination algorithms. To address this need, we investigate
the feasibility of using body schemas to carry out path planning in the vision space of the MAV. Body schemas
are a biologically-inspired approach, emulating the plasticity of the animal brains, allowing efficient represen-
tation of non-linear mapping between the body configuration space, i.e. its generalized coordinates and the
resulting sensory outputs. This paper presents a numerical experiment of generating landing trajectories of
a miniature rotor-craft using the notion of body and image schemas. More specifically, we demonstrate how
a trajectory planning can be executed in the image space using a pseudo-potential functions and a gradient-
based maximum seeking algorithm. It is demonstrated that a neural-gas type neural network, trained through
Hebbian-type learning algorithm can learn a mapping between the rotor-craft position/attitude and the output
of its vision sensors. Numerical simulations of the landing performance of a physical model is also presented,
The resulting trajectory tracking errors are less than 8 %.
1 INTRODUCTION
The applications of Miniature Air Vehicles (MAVs)
have widely diversified during the last five years.
They comprise both military and civilian, though the
latter has had a lower development rate. The main
goal of unmanned air vehicles (UAVs) is to provide a
remote and mobile extension of human perceptions,
allowing not only the security of the user (soldier,
policeman, cameraman, volcanologist), but also the
collection of valuable information of zones/targets of
interest used for on-line or off-line analysis. Ro-
torcraft MAVs represent an excellent alternative due
to their versatile flight profile as hovering, vertical
take-off/landing (VTOL) and maneuverability, allow-
ing the access to small enclosures and navigation
within unstructured environments. The enhanced pro-
ficiency of recently developed navigation and control
algorithms has brought about the possibility of using
VTOL MAVs in other civilian applications such as
wildlife studies, urban surveillance (car and pedes-
trian traffic), and pollution monitoring, to mention
just a few.
Despite the great number of potential MAV-based
applications, the operational role of these air robots
remains limited to being passive agents during their
missions such as in surveillance tasks. Enhancing the
current profile of MAVs implies endowing them with
the ability to perform autonomous decision making,
for example, an ability to establish a landing site, nav-
igate to it, and land/perch. To date, almost all MAV
research is carried out in a controlled laboratory en-
vironment where both the target landing location, as
well as the MAV position are measured in real-time
using a complex IR vision tracking system. If MAVs
are ever to exit the lab, their flight control needs to
be autonomous and based on on-board image and al-
titude sensors. To address this need, we proposed to
utilize a biologically inspired approach emulating the
plasticity of avian and human brain.
Traditionally, MAV controllers are derived from
linearized models of the vehicle. The stability of these
25
Enikov E. and Escareno J..
Application of Sensory Body Schemas to Path Planning for Micro Air Vehicles (MAVs).
DOI: 10.5220/0005547000250031
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 25-31
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

controllers is therefore limited to relatively small roll
and pitch angles, while in the case of fast maneuvers,
it is not guaranteed. Machine learning techniques
have been successful in learning models based on data
from human pilots (Abbeel et al., 2007), in improving
performance of control using reinforcement learning
(Lupashin et al., 2010), and exploring aggressive ma-
neuvers such as fast translation and back flip (Purwin
and D’Andrea, 2009; Gillula et al., 2011). In con-
trast to these prior efforts, the approach proposed here
does not simply replicate the control of human oper-
ators, rather, it is based on the premise that through
self-learning, the robot can create its own representa-
tion of its body and vision system and, upon a period
of training, can learn to perform such maneuvers on
its own. More specifically, we demonstrate the ap-
plication of an artificial neural network representa-
tion of the robot’s vision and attitude systems capa-
ble of controlling the robot to a target landing site.
The property of ANN to provide control laws through
implicit inversion of the robot’s kinematic chain or in
our case the non-linear transformation between vision
system’s output and the robot’s attitude and position
vectors is one of the main advantages of the proposed
ANN-based approach. The specific type of ANN ex-
plored here is a self-organizing map (SOM) where ar-
tificial neurons participate in a competitive learning
process, allowing the network to ”discover” the body
of the robot they describe. This process known as
body schema, originally developed in the field of cog-
nitive robotics, is a cornerstone of the proposed effort.
The concept of a body schema was first conceived
by Head and Holmes (Head and Holmes, 1911) who
studied how human perceive their bodies. Their defi-
nition of body schema is a postural model of the body
and its surface which is formed by combining infor-
mation from proprioceptive, somatosensory and vi-
sual sensors. According to their theory, the brain uses
this model to register the location of sensation on the
body and control its movements. A classical example
supporting the notion of body schema is the phantom
limb syndrome, where amputees report sensations or
pain from their amputated limb (Melzack, 1990; Ra-
machandran and Rogers-Ramachandran, 1996). Re-
cent brain imaging studies have indeed confirmed that
body schema is encoded in particular regions of the
primate and human brains (Berlucchi and Aglioti,
1997; Graziano et al., 2000) along with body move-
ments (Berthoz, 2000; Graziano et al., 2002). More
importantly, it is now apparent that the body schema is
not static, and can be modified dynamically to include
or ”extend” the body during use to tools (Iriki et al.,
1996) or when wearing a prosthetic limb (Tsukamoto,
2000). These and other advances of cognitive neuro-
science have led to the development of novel robot
control schemes.
The pliability of body schemas is one of the main
reasons a growing number of roboticists are explor-
ing the use of various schemas, i.e. motor, tactile,
visual in designing adaptable robots, capable of ac-
quiring knowledge of themselves and their environ-
ment. Recent experiments in cognitive developmental
robotics have demonstrated that using tactile and vi-
sion sensors, a robot could learn its body schema (im-
age) through babbling in front of a camera viewing its
arms, and subsequently, using a trained neuronal net-
work representing its motion scheme, acquire an im-
age of its invisible face through Hebbian self-learning
(Fuke et al., 2007). Yet another study demonstrated an
ability of a robot to extend its body schema to include
a tool (a stick), without a need to re-learn its forward
kinematics, rather, a simple shift in the sensory field
(schema) of the robot was sufficient to reproduce the
task of reaching a particular point in space with the
stick (Stoytchev, 2003).
In this paper we extend the computational ap-
proach introduced by Morasso (Morasso and San-
guineti, 1995) which creates a link between the
robot’s configuration and sensor spaces utilizing a
self-organizing map (SOM). In the case of an MAV, in
addition to the vision system, the MAV sensor space
includes vehicle’s pitch angle. The trained network is
then used to create a mapping between the configura-
tion and sensor spaces, thus presenting a self-learned
body schema. A unique feature of the approach is
that the robot control task does not require the use of
inverse kinematics, i.e. prediction of the robots’ po-
sition and orientation in the global Cartesian space.
Instead, through the use of a pseudo potential fields
defined in the sensor space , the MAV is controlled to
the desired landing position and orientation using an
implicit inversion of the non-linear mapping between
configuration and sensor spaces. These features of the
proposed control scheme are illustrated in a 3-DOF
planar MAV model described in the subsequent sec-
tions of this paper. In order to implement the proposed
approach it is required the fusion of inertial and visual
information, as demonstrated through simulations in
this paper.
2 SELF-ORGANIZING BODY
SCHEMA OF MAV-S
2.1 3-DOF MAV Model
The quadrotor is modeled as a 3D free-moving (trans-
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
26

lation and rotation) rigid body of mass m, concen-
trated at the center of gravity CG of the UAV. The mo-
tion of the flying robot can be expressed w.r.t. two co-
ordinate systems: (i) the inertial frame F
i
= (e
x
,e
z
)
T
,
and (ii) the body frame F
b
= (e
1
,e
3
)
T
, where e
u
,e
w
are the roll and yaw axes. An external translational
force vector T is exerted on rigid-body’s CG through
the collective thrust of the rotors. Likewise, a torque
τ
b
= (0, T )
T
is generated about CG by the differen-
tial thrust of the rotors. The equation modeling the
2D translational and rotational motion of the MAV
are given by the well-known expressions (for details
see (esc, 2007), (Goldstein, 1980) and (Fantoni and
Lozano, 2002))
˙
ξ
i
= V
i
(M + m)
˙
V
i
= U
ξ
∈ R
2
I
Y
¨
θ = U
θ
+ Γ
m
∈ R
1
(1)
where
˙
ξ = ( ˙x, ˙z)
T
represents the 2D translational ve-
locity of the drone, U
ξ
= R
θ
F
b
the projected thrust
vector used as control of the translational subsystem,
being F
b
= (0,T ), W
(M+m)
= (0,−(M + m)g)
T
is
the total weight vector, while Γ
m
corresponds to the
torque introduced by the gear,
Γ
m
= −mgl sin θ (2)
The MAV’s configuration coordinates are the lat-
eral and vertical positions of its center of mass, x, and
z, respectively, and its pitch angle, θ, (see Fig. 1).
The output of the vision system can be any feature in
Figure 1: 3DOF model of a planar rotor craft.
the image space, and in particular, the location of the
robot’s landing gear, G (represented as inverted Y in
Figure 1. For illustrative purposes and without loss
of generality, we consider an idealized vision system
where the coordinates of the MAV’s landing gear in
the camera’s image plane (x
C
,y
C
) are replaced with
the actual coordinates of the landing gear (x
G
,z
G
) in
the Cartesian space of motion of the MAV. Addition-
ally, the pitch angle θ is measured by an on-board in-
ertial measurement unit (IMU). The triplet (x
G
,y
G
,θ)
thus represents a fusion of vision and IMU sensor
data.
A non-linear transformation exists between the
generalized position of the center of mass determined
by the triplet (x,z,θ) and the location of the landing
gear
x
G
z
G
θ
=
x − L
G
sinθ
z − L
G
cosθ
θ
(3)
In what follows, we will demonstrate how an MAV
can learn transformation (3) using a self-organizing
body schema and apply the learned transformation to
navigate to a landing target.
2.2 Body and Sensor Schemas
The self-organizing body schema (So-BoS) links the
robot’s sensor space S with is configuration space C .
It utilizes a single C S -space=C × S to identify the
robot configuration as well as to plan motion in the
robot’s sensor space. A detailed review of applica-
tions of body schema-s in robotics can be found in
(Hoffmann et al., 2010). As an extension of the ap-
proach of Morasso (Morasso and Sanguineti, 1995)
and Stoychev (Stoytchev, 2003), in addition to vision
data, the sensor space includes vehicle attitude (pitch
angle θ), measured by an on-board artificial horizon
sensor or attitude gyro. Similar to conventional self-
organizing neural network maps, a layer of neurons
(processing units) is used to learn the mapping be-
tween the configuration space (generalized position of
the robot) and the output of the vision system (the lo-
cation of its landing gear). Unlike other topologically
ordered self-organizing maps such as the Kohonnen
map (Kohonen, 1982), the neurons in the present ap-
proach are initially disordered, i.e. forming a ‘’neural
gas” (Martinetz et al., 1991). The training process
modifies the weights of each neuron until the network
learns N body icons representing the C S -space. More
specifically, denoting by µ = [x,z,θ] the robot’s gen-
eralized position coordinates, and by β = [x
G
,z
G
,θ]
the vector of vision and attitude sensor outputs, then
for each body position i, the generalized coordinates
and associated sensors outputs will present an in-
stance of these two vectors ˜µ
i
= [ ˜x
i
, ˜z
i
,
˜
θ
i
] ∈ C and
˜
β
i
= [ ˜x
i
G
, ˜z
i
G
,
˜
θ
i
] ∈ S , respectively. The matched pairs
(
˜
β
i
, ˜µ
i
) ∈ C S are referred to as body icons. The C S
space is approximately by a field of N neurons, each
storing a learned body icon (
˜
β
i
, ˜µ
i
),i = 1,...N. As-
sociated with each neuron is an activation function,
U
i
(µ), which in this case is chosen to be the softmax
ApplicationofSensoryBodySchemastoPathPlanningforMicroAirVehicles(MAVs)
27

function given by
U
i
(µ) =
Gkµ − ˜µ
i
k
∑
j
G(kµ − ˜µ
i
k)
,
where G is a Gaussian function with variance σ
2
. The
normalization of U
i
(µ) ensures that it has a maximum
at µ = ˆµ
i
. The choice of σ determines the range of ac-
tivation of neighboring neurons when computing the
response of the network through
µ
approx
=
N
∑
j
˜µ
j
U
j
(µ). (4)
Similarly, the output of the sensory system is pro-
duced by
β
approx
(µ) =
N
∑
j
˜
β
j
U
j
(µ). (5)
The network training process is based on a compet-
itive learning process, where the N neurons are pre-
sented with a large number of pseudo-random training
vectors ˆµ
l
,l = 1, . . . I. In the present example N = 300
and I = 950. For each training cycle, all training
vectors ˆµ
l
are presented to the network and the body
icons are updated according to their respective learn-
ing laws
∆˜µ
j
= η
1
(ˆµ
l
− ˜µ
j
)U
j
(ˆµ
l
) (6)
and
∆
˜
β
j
(µ) = η
2
(β −
˜
β
j
)U
j
(ˆµ
l
). (7)
The parameters η
1
and η
2
are the learning rates for
each law, respectively. The competitive learning pro-
cess involves reduction of the learning rate as well as
the range of activation specified by σ as the training
proceeds. Through (5, the trained network represents
a mapping between the MAV-s generalized position
(C configuration space) and the resulting sensor space
S . Therefore, it is an implicit calibration procedure.
Figure 2 presents the 950 training vectors (blue dots)
and the learned body icons (green circles) upon train-
ing of N = 300 through N
T
= 50 training cycles. The
starting learning rates are η − 1 = η
2
= 3.84, with
variance σ
2
= 10/3. All three parameters were re-
duced linearly to 1/N
T
of their starting values at the
end of the last training epoch.
One of the greatest benefits from the trained neural
network and the associated mapping (5) is its ability
to generate robot trajectories in the sensor space with-
out explicitly computing its inverse Jacobian. This
property of the body-schema based approach is illus-
trated in the next section.
Figure 2: Training Set (blue dots) and Resulting Learned
Body Icons (green circles). Each green marker represents a
set of (x
G
,y
G
,θ) body icon (position) learned by its corre-
sponding neuron.
3 TRAJECTORY PLANNING IN
THE IMAGE SPACE
Upon training, each processing unit has its pre-
ferred body icon (
˜
β
i
, ˜µ
i
) allowing representation of
the MAV’s sensory output through (5). In addition to
the sensory output, the trained network can define ad-
ditional functions over the MAV’s configuration space
or the sensory space. One particularly interesting ap-
plication is path planning in the sensor space which
is useful for landing or navigation. The advantage of
the method is that the trained network does not re-
quire explicit inversion of the mapping between the
robot’s position and the output of the vision and navi-
gation sensors. Instead, the trajectory can be obtained
through solution of a ordinary differential equation
providing the position and velocity of the MAV. More
specifically, we use a pseudo-potential defined over
the vision space of the MAV defined through
ξ(µ) =
∑
j
˜
ξ
j
(
ˆ
β)U
j
(µ), (8)
where
˜
ξ
j
are scalar weights for each processing unit.
The potential weights can be selected such, that the
resulting pseudo-potential has an extrema (for exam-
ple maximum) at the target landing location. Then
a simple ordinary differential equation can be formu-
lated that has a maximum- or minimum-seeking so-
lution. Following the method of (Stoytchev, 2003),
we use a gradient ascend equation to drive the
MAV’s generalized coordinates to the maximum of
the pseudo-potential
˙µ = γ∇ξ(µ) = γ
N
∑
j=1
(˜µ
j
− µ)ξ
j
U
j
(µ). (9)
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
28

The desired landing location, including the landing
angle, can be specified by the choice of ξ
j
(
ˆ
β). The
right-hand side of (9) provides the velocities of the
MAV, while its solution generates the landing trajec-
tory.
To illustrate the approach, we have used two pos-
sible landing sites marked T1 and T2 in Figure 4.The
landing site T1 is at x
a
= 6,z
a
= 2,θ
a
= 0
◦
, while the
T2 is at x
a
= 19,z − a = 5,θ
a
= 30
◦
. The correspond-
ing pseudo-potential is defined as
ξ
a
(µ) =
1
kβ
a
− β(µ)k
, (10)
where β
a
= (x
a
,z
a
,θ
a
). The actual weights are com-
puted by evaluating (10) for each processing unit j,
i.e.
˜
ξ
j
= ξ
a
(˜µ
j
). The corresponding pseudo-potential
surface for target location T1 and T2 are shown in
Figure 3 (a) and (b), respectively.
(a)
(b)
Figure 3: Pseudopotential surface xi for target location T1
(a) and T2 (b). The surface is represented by a 4-th order
polynomial fit over the actual values of the potential func-
tion xi
i
marked with blue dots.
Solving equation (9) for each of the target landing
sites T1 and T2 results in 24 trajectories emanating
from S1-S12 for eatch of the two targets as shown in
Fig. 4.
4 EVALUATION OF
TRAJECTORY TRACKING
The data generated from the path-planning step de-
scribed in the previous section was fed into a cali-
Figure 4: Simulated robot paths to two different target loca-
tions (T1 and T2 ) in the robot’s vision space.The arrows in
the figure represent the MAV pitch angle.
brated model of a rotor-craft (Escareno et al., 2013).
The physical parameters of the MAV rotorcraft were
m = 0.4 kg, I
yy
= 0.177 kg-m
2
, operating in Earth’s
gravitational field g = 9.81 m/s
2
. Four resulting ac-
tual trajectories leading to the desired target T1 were
generated as shown in Figure 5. As can be observed
there is a transient error of approximately 1.5 m at
the beginning of some trajectories, along with a small
overshoot needed to absorb the kinetic energy of the
rotor-craft. A complementary test was carried out to
observe the behavior of the proposed approach with
respect to a classical regulation problem. Figures 7
depict the performance of the NN-based tracking and
the regulation controllers to reach the landing coordi-
nates. In such figure it is observed that angular behav-
ior is smooth compared with classical angular regula-
tion.
Figure 5: MAV trajectory tracking performance using the
ANN-generated landing trajectories to T2.
ApplicationofSensoryBodySchemastoPathPlanningforMicroAirVehicles(MAVs)
29
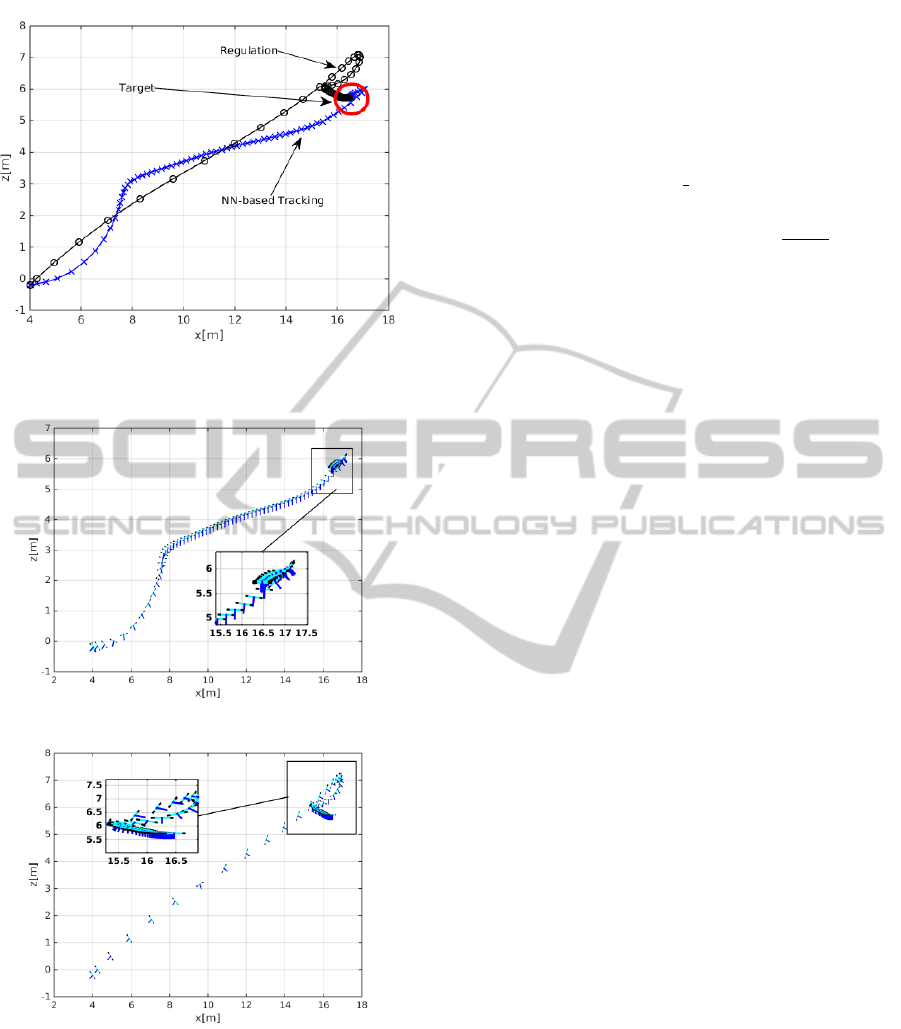
Figure 6: Comparative between the NN-based tracking and
a classical regulation control.
(a)
(b)
Figure 7: Behavior of the rotorcraft: [a] NN-bases tracking
control [b] Classical regulation.
4.1 Two-Time Scale Controller
It has been used a classical two-time scale controller
to fulfill the tracking objective for the translational dy-
namic subsystem (1a), where it is defined a linear be-
havior through stable error polynomials u
x
(e
x
, ˙e
x
) and
u
z
(e
z
, ˙e
z
) as presented in (Sepulchre et al., 1997).
¨x = T sinθ := u
x
(e
x
, ˙e
x
)
¨z = T cosθ − g := u
z
(e
z
, ˙e
z
)
(11)
with u
x
= k
p
x
e
x
+ k
v
z
˙e
x
and u
z
= k
p
z
e
z
+ k
v
z
˙e
z
. Such
stable linear behavior is achieved if
T =
u
2
x
+ (u
z
+ g)
1
2
(12)
θ = θ
d
(t) with θ
d
(t) = arctan
r
1
r
2
+ g
(13)
with k
p
q
, k
p
z
and k
v
z
are positive constants. The lat-
ter assumes a time-scale separation between transla-
tion (slow dynamics) and rotational (fast dynamics)
motion. The latter assumes a time-scale separation
between translation (slow dynamics) and rotational
(fast dynamics) motion. Thus, from the error variable
¯
θ = θ − θ
d
arises the following dynamics
¨
¯
θ = τ
θ
−
¨
θ
d
(14)
where
¨
θ
d
is disregarded to avoid aggressive com-
mands. The controller aims to track θ
d
(t) while com-
pensating the torque induced by the gear, for this pur-
pose it is used the controller
u
θ
= −k
p
θ
e
θ
− k
v
θ
˙e
θ
+ mgl sin θ (15)
5 SUMMARY AND
CONCLUSIONS
The application of self-organizing artificial neural
networks to the problem of path planning of MAV-s
have been described. It has been demonstrated that
the neural network can fuse seamlessly the informa-
tion gathered from different sensory outputs such as
vision and attitude sensors. Upon training period
comprised of carrying out pseudo-random motions,
akin birds learning how to fly, the MAV can learn
landing maneuvers leading to the desired landing po-
sition. The accuracy of the landing has been found
to depend on the number of nodes used in the arti-
ficial neural network as well as the training parame-
ters such as learning rate and range of activation of
the neuronal network. The resulting trajectories of
the physical model show transient errors of approxi-
mately 8 % (1 .5 m over a landing target at 18 m) and a
small overshoot of 0.7 m (4. %) required to reduce the
landing speed. Due to its low computational demand
upon completion of the ANN training, the proposed
method is likely to find application in the develop-
ment of bio-inspired MAV-s capable of autonomous
navigation using low-cost vision and attitude sensors.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
30

ACKNOWLEDGEMENTS
The authors acknowledge the support of IPSA in host-
ing one of the authors (Enikov) during his sabbatical
leave allowing the development of this collaborative
research project as well as partial support from NSF
grant # 1311851 related to the development of ANN
simulation library.
REFERENCES
(2007). Embedded control system for a four rotor UAV, vol-
ume 21.
Abbeel, P., Coates, A., Quigley, M., and Ng, A. Y. (2007).
An application of reinforcement learning to aerobatic
helicopter flight. Advances in neural information pro-
cessing systems, 19:1.
Berlucchi, G. and Aglioti, S. (1997). The body in the brain:
neural bases of corporeal awareness. Trends in neuro-
sciences, 20(12):560–564.
Berthoz, A. (2000). The brain’s sense of movement. Har-
vard University Press.
Escareno, J., Rakotondrabe, M., Flores, G., and Lozano,
R. (2013). Rotorcraft mav having an onboard ma-
nipulator: Longitudinal modeling and robust control.
In Control Conference (ECC), 2013 European, pages
3258–3263. IEEE.
Fantoni, I. and Lozano, R. (2002). Nonlinear control for
underactuated mechanical systems. Springer.
Fuke, S., Ogino, M., and Asada, M. (2007). Body image
constructed from motor and tactile images with vi-
sual information. International Journal of Humanoid
Robotics, 4(02):347–364.
Gillula, J. H., Huang, H., Vitus, M. P., and Tomlin, C. J.
(2011). Design and analysis of hybrid systems, with
applications to robotic aerial vehicles. In Robotics Re-
search, pages 139–149. Springer.
Goldstein, H. (1980). Classical mechanics. Addison-
Wesley.
Graziano, M. S., Cooke, D. F., and Taylor, C. S. (2000).
Coding the location of the arm by sight. Science,
290(5497):1782–1786.
Graziano, M. S., Taylor, C. S., and Moore, T. (2002). Com-
plex movements evoked by microstimulation of pre-
central cortex. Neuron, 34(5):841–851.
Head, H. and Holmes, G. (1911). Sensory disturbances
from cerebral lesions. Brain, 34(2-3):102–254.
Hoffmann, M., Marques, H. G., Hernandez Arieta, A.,
Sumioka, H., Lungarella, M., and Pfeifer, R. (2010).
Body schema in robotics: a review. Autonomous Men-
tal Development, IEEE Transactions on, 2(4):304–
324.
Iriki, A., Tanaka, M., and Iwamura, Y. (1996). Coding of
modified body schema during tool use by macaque
postcentral neurones. Neuroreport, 7(14):2325–2330.
Kohonen, T. (1982). Self-organized formation of topolog-
ically correct feature maps. Biological cybernetics,
43(1):59–69.
Lupashin, S., Schollig, A., Sherback, M., and D’Andrea,
R. (2010). A simple learning strategy for high-speed
quadrocopter multi-flips. In Robotics and Automa-
tion (ICRA), 2010 IEEE International Conference on,
pages 1642–1648. IEEE.
Martinetz, T., Schulten, K., et al. (1991). A” neural-gas”
network learns topologies. University of Illinois at
Urbana-Champaign.
Melzack, R. (1990). Phantom limbs and the concept of a
neuromatrix. Trends in neurosciences, 13(3):88–92.
Morasso, P. and Sanguineti, V. (1995). Self-organizing body
schema for motor planning. Journal of Motor Behav-
ior, 27(1):52–66.
Purwin, O. and D’Andrea, R. (2009). Performing aggres-
sive maneuvers using iterative learning control. In
Robotics and Automation, 2009. ICRA’09. IEEE In-
ternational Conference on, pages 1731–1736. IEEE.
Ramachandran, V. S. and Rogers-Ramachandran, D.
(1996). Synaesthesia in phantom limbs induced with
mirrors. Proceedings of the Royal Society of London.
Series B: Biological Sciences, 263(1369):377–386.
Sepulchre, R., Jankovic, M., and Kokotovic, P. (1997). Con-
structive Nonlinear Control. Springer-Verlag.
Stoytchev, A. (2003). Computational model for an extend-
able robot body schema.
Tsukamoto, Y. (2000). Pinpointing of an upper limb pros-
thesis. JPO: Journal of Prosthetics and Orthotics,
12(1):5–6.
ApplicationofSensoryBodySchemastoPathPlanningforMicroAirVehicles(MAVs)
31
