
Unconstrained Global Optimization: A Benchmark Comparison of
Population-based Algorithms
Maxim Sidorov
1
, Eugene Semenkin
2
and Wolfgang Minker
1
1
Institute of Communication Engineering, Ulm University, Ulm, Germany
2
Institute of System Analysis, Siberian State Aerospace University, Krasnoyarsk, Russia
Keywords:
Genetic Algorithm, Evolution Strategy, Cuckoo Search, Differential Evolution, Particle Swarm Optimization,
Benchmark Comparison, Unconstrained Optimization.
Abstract:
In this paper we provide a systematic comparison of the following population-based optimization techniques:
Genetic Algorithm (GA), Evolution Strategy (ES), Cuckoo Search (CS), Differential Evolution (DE), and
Particle Swarm Optimization (PSO). The considered techniques have been implemented and evaluated on a
set of 67 multivariate functions. We carefully selected the tested optimization functions which have different
features and gave exactly the same number of objective function evaluations for all of the algorithms. This
study has revealed that the DE algorithm is preferable in the majority of cases of the tested functions. The
results of numerical evaluations and parameter optimization are presented in this paper.
1 INTRODUCTION
Evolutionary and behavioural algorithms such as GA,
ES, PSO, CS, and DE have recently been success-
fully applied to a wide variety of problems includ-
ing machine learning, multi-modal function optimiza-
tion, the evolution of complex structures such as ar-
tificial neural networks or even computer programs.
However, one of the most significant weaknesses of
these algorithms is the necessity of setting the opti-
mal parameters and selecting the suitable algorithm in
each specific real-world problem. Moreover, it could
be difficult to optimize high-dimensional, multivari-
ate functions using the mentioned algorithms due to a
large number of local extrema, the surface of a com-
plex function, etc.
In this paper we performed a comparative study
where we dealt with the most popular population-
based algorithms. In order to fairly compare the con-
sidered algorithms we performed an optimization pro-
cess using 67 functions which are considered to be
difficult for optimization. We gave the same number
of function evaluations for all the algorithms and car-
ried out an optimization of the parameters for all of
the algorithms. To enhance the statistical reliability
of the experiments we repeated the process of func-
tion optimization 100 times with each combination of
parameters. The study revealed that the DE algorithm
was generally found to perform better than other al-
gorithms.
The rest of the paper is organized as follows: Sig-
nificant related work is presented in Section 2. We
briefly describe the used algorithms in Section 3. Fur-
ther, the set up of the experiments, their results, and
the used functions are in Section 4. Finally, Section 5
presents the conclusion and future work.
2 SIGNIFICANT RELATED
WORK
The comparison of the population-based optimization
algorithms is a focus of scientific groups all over the
world.
Thus, the authors in (Eberhart and Shi, 1998)
compared the PSO algorithm with GA in a theoretical
way. In this paper the individual features of the algo-
rithms were highlighted, moreover the authors noted
that the performance of one algorithm might be im-
proved by incorporating features of the other.
In (Elbeltagi et al., 2005) a comparison of five
evolutionary-based optimization algorithms was pre-
sented. The authors researched the following algo-
rithms: GA, memetic algorithms, PSO, Ant-Colony
Optimization, and the Shuffled Frog Leaping Al-
gorithm. Two benchmark continuous optimization
test problems were solved using the considered algo-
230
Sidorov M., Semenkin E. and Minker W..
Unconstrained Global Optimization: A Benchmark Comparison of Population-based Algorithms.
DOI: 10.5220/0005548002300237
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 230-237
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

rithms. The authors concluded that the PSO method
was generally found to perform better than other al-
gorithms. Among some weaknesses of the study one
may note that only two test functions could not give
statistical reliable results.
3 OPTIMIZATION ALGORITHMS
OF DIRECT SEARCH
In this section we present a brief description of the
used algorithms. Suppose that the given objective
function is f (x), where x = (x
1
, ..., x
n
).
3.1 Cuckoo Search
CS is a population-based optimization method devel-
oped in (Yang and Deb, 2009) which imitates the be-
haviour of cuckoos in their natural habitats utilizing
the concept of Levy flight. Cuckoos lay their eggs in
other birds’ nests and rely on other birds to raise their
offspring. It is believed that such selfish behaviour in-
creases the survival rate of the cuckoo’s genes since
the cuckoo needs not spend any energy and time rais-
ing its offspring. Thus, the time and energy saved
can be used by the cuckoo in order to breed and lay
more eggs (Lidberg, 2011). Nevertheless, there exist
special strategies which allow the birds to detect the
invading eggs. The CS algorithm uses this behaviour
to traverse the search space, looking for the optimal
solution. CS consists of the following stages:
Step 1. Initialization
A pool of initial solutions should better cover the
whole search space by uniformly randomizing within
the area which is constrained by the given lower and
upper boundaries. Practically, each j −th component
of the initial i −th solution is formed in conformity
with the following equation:
x
j
i,0
= x
j
min
+ r(0, 1) ×(x
j
max
−x
j
min
) , (1)
where, x
j
max
and x
j
min
are the corresponding bound-
aries of the j −th variable, and r(0, 1) is a uniformly
distributed random variable from [0, 1]. Then, initial
solutions should be evaluated in order to obtain the
current best.
Step 2. Generate a Solution by Levy Flights
After the initialization and the first assessment steps,
new solutions should be generated by Levy walk
around the best solution obtained so far:
x
i
= x
i−1
+ N(0,1) ×
0.01 ×
σ ×N(0.1)
|N(0,1)|
1
β
×(x
i−1
−x
best
)
!
,
where
σ =
Γ(1 + β)sin
πβ
2
Γ
1+β
2
β2
(β−1)
2
1
β
,
Γ(z) is gamma function, 1 ≤ β ≤ 2, N(0, 1) is a nor-
mal distributed n-dimensional vector with µ = 0 and
σ
2
= 1, x
i
and x
i−1
are the current and previous solu-
tions, x
best
is the best solution found so far, and all the
operations with vectors are element-based.
Step 3. Evaluate Quality of Solutions
At this point all the new solutions should be evaluated
and in case of improvement in the value of the objec-
tive function, the old solution should be replaced by
the new one.
Step 4. Discovery and Randomization
Now, new solutions should be discovered with the
given probability pa:
x
i
=
(
x
i−1
, if r(0, 1) < pa
x
i−1
×r(0, 1) ×(x
n
−x
m
), otherwise.
where x
n
and x
m
are randomly chosen different solu-
tions, they must be distinct from each other, and pa is
the discovery rate of alien solutions (or eggs).
Step 5. Rank the Solutions
Here all the current solutions should be ranked and
the global best is saved.
The Steps 2 to 5 are repeated until the stop cri-
terion is True. Only two parameters should be sup-
plied to the algorithm, the discovery rate of alien eggs
pa ∈[0, 1] and the size of population. Pa plays an im-
portant role controlling the elitism and the trade-off
between randomization and local search (Yang and
Deb, 2010). In this study we used the grid technique
for optimization of the pa parameter form [0, 1] with
the step equal to 0.1, and only two values for the size
of population, namely 25 and
√
bud, where bud is the
number of objective function evaluations.
3.2 Differential Evolution
DE is a simple yet powerful evolution algorithm for
unconstrained global optimization introduced and dis-
cussed in (Storn and Price, 1995), (Storn and Price,
1997), and (Price et al., 2006). CS consists of the fol-
lowing stages:
UnconstrainedGlobalOptimization:ABenchmarkComparisonofPopulation-basedAlgorithms
231

Step 1. Initialization
This step should be done in a similar to way how it
was done in the case of CS (see Equation 1).
Step 2. Compute the Potentially New Position
Further, depending on the selected strategy apply the
following formula in order to get a new solution x
i, j
:
DE/rand/1
x
i, j
= x
i−1,c
+ w ×(x
i−1,a
−x
i−1,b
) ,
DE/local-to-best/1
x
i, j
= x
i−1, j
+ w ×(x
i−1,best
−x
i−1, j
)
+ w ×(x
i−1,a
−x
i−1,b
) ,
DE/best/1 with jitter
x
i, j
= x
i−1,best
+ (x
i−1,a
−x
i−1,b
)
×(0.001 ×r(0, 1) + w) ,
DE/rand/1 with per-vector-dither
x
i, j
= x
i−1,c
+ (x
i−1,a
−x
i−1,b
)
×(1 −w) ×r(0, 1) + w ,
DE/rand/1 with per-generation-dither
x
i, j
= x
i−1,c
+ (x
i−1,a
−x
i−1,b
)
×(1 −w) ×r(0, 1) + w ,
Either-or-algorithm
x
i, j
=
x
i−1,c
+ w ×(x
i−1,a
−x
i−1,b
), ifr(0, 1) < 0.5
x
i−1,c
+ 0.5 ×(w + 1)
×(x
i−1,a
+ x
i−1,b
−2x
i−1,c
) , otherwise.
where x
i−1,a
, x
i−1,b
, and x
i−1,c
are three randomly
picked solutions from the previous iteration, they
must be distinct from each other. Practically, it can
be done by a random solution permutation within the
whole population. x
i−1,best
is the best solution from
the previous iteration, w is the step size, usually from
[0, 2].
Step 3. Crossover
Next, the obtained solutions should be placed in the
next generation with the given crossover probability
cr.
x
i, j
=
(
x
i, j−1
, ifr(0, 1) <cr
x
i, j
, otherwise.
Step 4. Rank the Solutions
Here all the current solutions should be ranked and
the global best is saved.
The Steps 2 to 4 should be repeated until the stop
criterion is True.The choice of DE parameters cr, w,
the number of solutions in each generation and the
new solution generation strategy can have a large im-
pact on optimization performance. In this study we
used all types of strategies, as well as cr and w param-
eters from [0,1] with the step equal to 0.1. A constant
number of solutions in each generation has been set
as
√
bud.
3.3 Evolution Strategy
The ES which was proposed by Schwefel, and
Rechenberg (Beyer and Schwefel, 2002) operates
with real numbers directly. We implemented the ES
algorithm based on (Haupt and Haupt, 2004) and
(Back, 1996). The ES comprises the following steps:
Step 1. Initialization
This step should be done in a similar way to how it
was done in the case of CS and DE (see Equation 1).
Step 2. Recombination
Further, depending on the selected recombination
strategy apply the following formula in order to get
a new solution x
i, j
and the corresponding parameters
σ
i, j
and α
i, j
:
No recombination
x
i, j
= x
i−1,r(1,µ)
,
where j = 1...λ, and r(1, µ) is a uniform distributed
random variable from [1, µ].
Discrete recombination
This type of recombination determines the k−th com-
ponent of the recombinant exclusively by the k −th
component of the randomly (uniformly) chosen two
parent individuals (Beyer and Schwefel, 2002):
x
i, j,k
= x
i−1,r(1,µ),k
.
Panmictic discrete recombination
The same as above, but in this case more than two
parents can be selected in order to produce the cur-
rent offspring.
Intermediate recombination
Intermediate recombination calculates the average
values of the corresponding components of the two
parent vectors.
Panmictic intermediate recombination
Again, the same as the previous one, but in this case
more than two parents can be selected in order to pro-
duce the current offspring.
Generalized intermediate recombination
x
i, j
= x
i−1,a
+ r(0, 1) ×(x
i−1,b
−x
i−1,a
), (2)
where x
i−1,a
, x
i−1,b
are randomly selected solutions
from the previous generation, r(0, 1) is as usually a
uniform distributed variable from [0, 1].
Generalized intermediate recombination
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
232

The same as the previous one, but now more than two
parents can be selected in order to produce the current
offspring using Equation 2.
In order to simplify a description of the algorithm,
only solution-based formulas have been displayed, it
should be noted that the corresponding parameters
σ
i, j
and α
i, j
are converted in exactly the same way
as was done for the position variables.
Step 3. Mutation
Mutation is used to ensure the evolutionary diversity
and has been implemented using Equation 2.18 from
(Back, 1996).
Step 4. Selection
In this study we used the standard (µ, λ)and(µ + λ)
selection types.
Step 5. Rank the Solutions
Here all the current solutions should be ranked and
the global best is saved.
The Steps 2 to 5 should be repeated until the stop cri-
terion is True. Regarding the parameters of the ES
procedure, we tried all types of recombination for so-
lutions and parameters independently. The last pa-
rameter is the type of selection.
3.4 Genetic Algorithm
GA, which was originally conceived by Holland (Hol-
land, 1975), represents an abstract model of Dar-
winian evolution where a candidate solution (or indi-
vidual) is encoded with the boolean values (or genes).
In case of pseudo-boolean GA, each gene is filled
with boolean true with the probability equal to 0.5 and
with false otherwise. Let Lower and Upper be the cor-
responding boundaries of the search space and Accu-
racy be the desirable accuracy of the optimal solution.
Then, the necessary number of bits for encoding (N)
is equal to the lowest value for which the following
equation is true:
2
N
≥
U pper −Lower
0.1 ×Accuracy + 1
, (3)
thus, each GA’s individual is (n × N)-dimensional
boolean vector, where n is the number of variables
in the optimization task.
A pool of initial individuals (or population) should
better cover the whole search space by uniformly ran-
domizing within the area which is constrained by the
given lower and upper boundaries. Practically, each
gene is filled with boolean true with the probability
equal to 0.5 and with false otherwise.
The next phase is assessment of each solution.
For this reason, each Boolean vector should be de-
coded to an integer vector either with the conventional
boolean-to-integer encoding scheme or with Gray
coding (Gray, 1953). Lastly, to produce the real val-
ues the corresponding interval from [Lower,U pper]
should be selected. The resulting real vector is used
to obtain the current value of the objective function.
Intuitively, the lower the value of the objective
function, the higher the probability that there is a
corresponding individual. For this reason, the selec-
tion procedure should be applied in order to enhance
the probability of including the perspective candidates
into the next generation of GA. We used three differ-
ent strategies of the selection procedure. Proportional
and rank selections operate with the absolute and rank
values of current solutions respectively. It means that
the higher the fitness value or corresponding rank,
which can be obtained by the sorting procedure, the
higher the probability that it is selected. Whereas in
tournament selection, the individual with the higher
fitness function from the group with n individual is
selected into the next generation. The recombination
procedure provides the similarity of the individuals in
the next generation to the best individuals from the
previous one. Lastly, mutation supports the evolution
diversity of individuals.
The described procedure is repeated until the ter-
minate condition is true.
We optimized all the parameters: accuracy,
elitism, Gray coding, types of mutation, selection and
recombination.
3.5 Particle Swarm Optimization
Being a behavioural algorithm, the PSO technique
(Kennedy et al., 1995) simulates the behaviour of ani-
mal swarms in their natural habitats. The algorithm
optimizes a function by having a number of solu-
tions or particles and moving these particles within
the search-space according to the mathematical for-
mulas. Each particle is characterised by position and
velocity values. The movement of a particular solu-
tion within the search-space is influenced by its local
best known position and the global best known posi-
tion in the search-space, which was achieved by other
particles. More precisely, the following formulas de-
termine the velocity and position of each particle dur-
ing the algorithm flow:
v
i,d
= wv
i,d
+ c
1
r
1
(p
i,d
−x
i,d
) + c
2
r
2
(g
d
−x
i,d
) , (4)
x
i
= x
i
+ v
i
, (5)
where v
i,d
is the d −th velocity component of the i −
th particle, p
i,d
is the d −th local best element of the
i −th particle, g
d
is the d −th global best component
of the i −th particle. r
1
and r
2
are normal-distributed
UnconstrainedGlobalOptimization:ABenchmarkComparisonofPopulation-basedAlgorithms
233
variables with mean equal to 0 and variance equal to
1, while w, c
1
and c
2
are parameters of the algorithm
to be optimized.
Moreover, an absolute value of the velocity is al-
ways limited by the VelocityMax. In our implementa-
tion this parameter was determined by the following
formula:
VelocityMax = k
(U pper −Lower)
2
,
where U pper and Lower are the corresponding
boundaries of the search-space, k is the fourth param-
eter to be optimized.
All the described algorithms have been tested us-
ing 67 test functions with different features and di-
mensionalities.
4 THE USED APPROACH
All the considered algorithms were implemented
from scratch on C++ language using the Boost library.
We adopted the MVF Library (Adorio and Diliman,
2005) to deal with the benchmark test function.
There are a number of standard functions (Adorio
and Diliman, 2005) which have different features and
are difficult to optimize. The community uses such
functions to examine the optimization ability of de-
veloped algorithms.
The suggested baseline implementation of GA,
ES, CS, DE and PSO has been tested on 67 multi-
variate functions for unconstrained global optimiza-
tion. The selected functions are listed in Table 2,
where Opt. and D. stand for the optimal value and the
function dimensionality correspondingly. It should be
noted that the corresponding formulas can be found
here (Adorio and Diliman, 2005).
Some functions can be characterized in the follow-
ing way.
Many Local Minima. The Ackly function is char-
acterized by a nearly flat outer region, and a large
hole at the centre. The function poses a risk for
optimization algorithms of being trapped in one of
its many local minima. The Griewank function has
many widespread local minima, which are regularly
distributed. The Rastrigin function has several local
minima. It is highly multi-modal, but the locations of
the minima are regularly distributed.
Bowl-shaped. The Bohachevsky functions are
slightly different but all of them have the same similar
bowl shape. The Sphere function has 2 local minima
in addition to the global one. It is continuous, con-
vex and unimodal. The Sum Squares function, also
referred to as the Axis Parallel Hyper-Ellipsoid func-
tion, has no local minimum except the global one.
Plate-shaped. The Booth function is plate-
shaped. The Matyas and Zakharov functions have no
local minima except the global one.
Valley-shaped. The Rosenbrock function is re-
ferred to as the Valley or Banana function, and is a
popular test problem for gradient-based optimization
algorithms. The function is unimodal, and the global
minimum lies in a narrow, parabolic valley. However,
even though this valley is easy to find, convergence to
the minimum is difficult.
In fact, the efficiency of an optimization algorithm
highly depends on its parameters, therefore the pa-
rameters of standard algorithms have been optimized
with the brute force approach using the grid tech-
nique. The optimized parameters and their potential
values can be found in Table 1.
Table 1: Parameters optimization setup, with the abbrevia-
tions of parameters in parentheses.
Parameter Values
CS
pa [0.1, 0.2, ..., 1.0]
DE
Crossover probabil-
ity (CR)
[0, 0.1, ..., 1.0]
Stepsize weight (W) [0, 0.1, ..., 1.0]
Strategy (S) rand/1, local-to-best/1, best/1 with
jitter, rand/1 with per-vector-dither,
rand/1 with per-generation-dither,
rand/1 either-or-algorithm
ES
Variable Recombi-
nation (VR)
Without, discrete, panmictic discrete,
intermediate, panmictic intermediate,
generalized intermediate, panmictic
generalized intermediate
Parameter Recombi-
nation (PR)
The same as above
Selection (P) (µ, λ), (µ + λ)
GA
Gray (G) false, true
Elitism (E) false, true
Selection (S) proportional, rank, tournament
Recombination (R) one-, two-points, uniform
Mutation (M) weak, normal, strong
Accuracy (A) [0.001, 0.0001]
Tournament (T) [2, 3, ..., 5]
PSO
c
1
[1.5, 1.6, ..., 1.9]
c
2
[1.5, 1.6, ..., 1.9]
k [0.1, 0.3, ..., 0.9]
w [0.8, 0.9, ..., 1.1]
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
234

Table 2: The used function and their description. D. stands for dimensionality, Lower, Upper are the corresponding boundaries
of the search-space, and Opt. is an optimal value of the function.
Function D. Lower Upper Opt. Function D. Lower Upper Opt.
Ackley 2 -32.768 32.768 0 NeumaierPerm0 2 -1 1 0
Beale 2 -4.5 4.5 0 NeumaierPowersum 2 0 4 0
Bohachevsky1 2 -100 100 0 NeumaierTrid 2 -4 4 -2
Bohachevsky2 2 -100 100 0 Paviani 2 0.001 9.999 -45.778
Booth 2 -10 10 0 QuarticNoiseU 2 -1.28 1.28 0
BoxBetts 3 0.9 11.2 0 QuarticNoiseZ 2 -1.28 1.28 differ
Branin 2 -5 15 0.398 Rastrigin 2 -5.12 5.12 0
Branin2 2 -5 15 0 Rastrigin2 2 -5.12 5.12 0
Camel6 2 -5 5 -1.032 Rosenbrock 2 -10 10 0
Cola 17 -4 4 11.746 Schaffer1 2 -100 100 0
Colville 4 -10 10 0 Schaffer2 2 -100 100 0
Corana 4 -1000 1000 0 Schwefel1 2 2 -10 10 0
Easom 2 -100 100 -1 Schwefel2 21 2 -10 10 0
Exp2 2 0 20 0 Schwefel2 22 2 -10 10 0
FraudensteinRoth 2 -20 20 0 Schwefel2 26 2 -500 500 -12569.5
Gear 4 12 60 0 Shekel10 10 0 10 0
GeneralizedRosenbrock 2 -10 10 0 Shekel4 10 4 0 10 -10.536
GoldsteinPrice 2 -2 2 3 Shekel4 5 4 0 10 -10.153
Griewank 2 -100 100 0 Shekel4 7 4 0 10 -10.403
Hansen 2 -10 10 -176.54 Shubert 2 -10 10 -24.063
Hartman3 3 0 1 -3.86 Shubert2 2 -10 10 -186.731
Hartman6 6 0 1 -3.32 Shubert3 2 -10 10 -24.063
Himmelblau 2 -5 5 0 Sphere 2 -10 10 0
Holzman2 2 -10 10 0 Sphere2 2 -10 10 0
Hyperellipsoid 2 -1 1 1 Step 2 -100 100 0
Kowalik 4 -5 5 0 StretchedV 2 -10 10 0
Langerman 2 0 10 -1.4 SumSquares 2 -10 10 0
Leon 2 -10 10 0 Trecanni 2 -5 5 0
Matyas 2 -10 10 0 Trefethen4 2 -6.5 6.5 -3.307
Maxmod 2 -10 10 0 Watson 6 -10 10 0.002
McCormick 2 -3 4 -1.913 Xor 9 -10 10 0
Michalewitz 2 0 π -1.932 Zettl 2 -10 10 -0.004
Multimod 2 -10 10 0 Zimmerman 2 -100 100 0
NeumaierPerm 2 -2 2 0
We applied the grid optimization scheme in order
to find out the best parameters of each algorithm and
test function. For every combination of the optimized
parameters we repeated the optimization process 100
times to obtain statistical significant results. We gave
the same number of objective function evaluations for
all the algorithms. Namely, Num = 100 ×n
2
, where n
is the dimensionality of the test function.
The results of test function optimization with the
optimal parameters of algorithms is in Figure 1 where
only average (over 100 algorithm runs) values are
shown. The best values are highlighted with darker
colours. The lower the value, the darker the corre-
sponding cell.
5 CONCLUSIONS
Regarding the results of standard algorithm applica-
tions one may conclude that DE is the best algorithm.
The optimal parameters were a wide variety of all
possible settings. However, CR equal to 0.1, W to
0.6 and the rand/1 either-or strategy seem to be an
optimal choice for majority of the functions. Never-
theless, for some optimization functions DE was out-
performed by GA and PSO (see Figure 1).
It should be noted that in the case of GA the tour-
nament selection as well as the (µ + λ) selection for
ES were always selected as the optimal choice for all
of the functions.
One of the possible further directions of investi-
gation might be the usage of a cooperative scheme,
where each algorithm might use the features of oth-
ers in order to improve the performance as was done
here (Sidorov et al., 2014b) for GA, ES and PSO
only and in (Akhmedova and Semenkin, 2013) for
PSO-like algorithms. Moreover, an implementation
of the self-adaptive operators for evolution algorithms
(Sidorov et al., 2014a), (Semenkin and Semenkina,
2012) could significantly simplify the process of set-
UnconstrainedGlobalOptimization:ABenchmarkComparisonofPopulation-basedAlgorithms
235
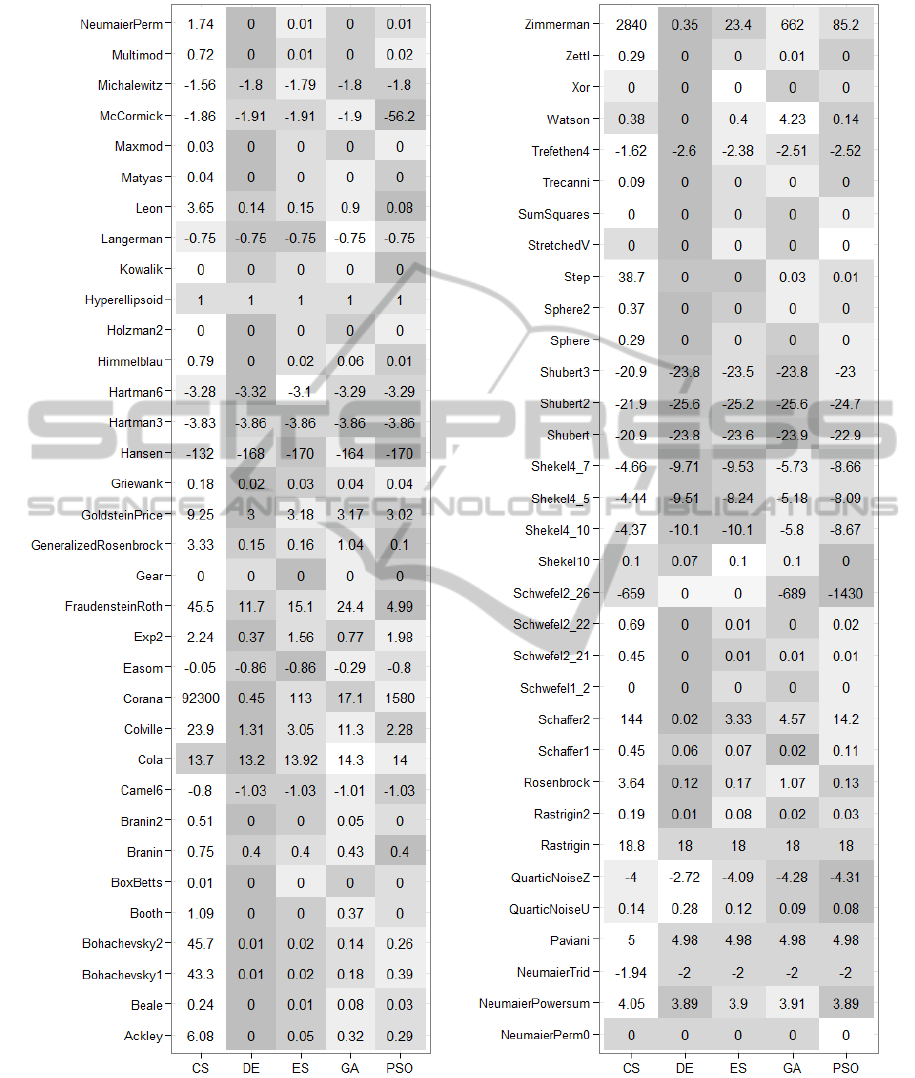
Figure 1: Means of the minimum values over 100 runs of the corresponding algorithm with all possible combinations of
the considered parameters. The darker cell, the better solution was found with the optimal parameters of the corresponding
algorithm. The best values are highlighted with gray colour, the worst ones are coloured with white colour.
ting parameters. Such algorithms could also be in-
cluded in cooperative schemes.
REFERENCES
Adorio, E. P. and Diliman, U. (2005). Mvf-multivariate test
functions library in c for unconstrained global opti-
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
236

mization.
Akhmedova, S. and Semenkin, E. (2013). Co-operation of
biology related algorithms. In Evolutionary Compu-
tation (CEC), 2013 IEEE Congress on, pages 2207–
2214. IEEE.
Back, T. (1996). Evolutionary algorithms in theory and
practice. Oxford Univ. Press.
Beyer, H.-G. and Schwefel, H.-P. (2002). Evolution
strategies–a comprehensive introduction. Natural
computing, 1(1):3–52.
Eberhart, R. C. and Shi, Y. (1998). Comparison between
genetic algorithms and particle swarm optimization.
In Evolutionary Programming VII, pages 611–616.
Springer.
Elbeltagi, E., Hegazy, T., and Grierson, D. (2005).
Comparison among five evolutionary-based optimiza-
tion algorithms. Advanced engineering informatics,
19(1):43–53.
Gray, F. (1953). Pulse code communication. US Patent
2,632,058.
Haupt, R. L. and Haupt, S. E. (2004). Practical genetic
algorithms. John Wiley & Sons.
Holland, J. H. (1975). Adaptation in natural and artificial
systems: An introductory analysis with applications to
biology, control, and artificial intelligence. U Michi-
gan Press.
Kennedy, J., Eberhart, R., et al. (1995). Particle swarm op-
timization. In Proceedings of IEEE international con-
ference on neural networks, volume 4, pages 1942–
1948. Perth, Australia.
Lidberg, S. (2011). Evolving cuckoo search: From single-
objective to multi-objective.
Price, K., Storn, R. M., and Lampinen, J. A. (2006). Differ-
ential evolution: a practical approach to global opti-
mization. Springer Science & Business Media.
Semenkin, E. and Semenkina, M. (2012). Self-configuring
genetic algorithm with modified uniform crossover
operator. In Advances in Swarm Intelligence, pages
414–421. Springer.
Sidorov, M., Brester, K., Minker, W., and Semenkin, E.
(2014a). Speech-based emotion recognition: Feature
selection by self-adaptive multi-criteria genetic algo-
rithm. In International Conference on Language Re-
sources and Evaluation (LREC).
Sidorov, M., Semenkin, E., and Minker, W. (2014b). Multi-
agent cooperative algorithms of global optimization.
In Proceedings of the 11th International Conference
on Informatics in Control, Automation and Robotics
(ICINCO), volume 1, pages 259–265.
Storn, R. and Price, K. (1995). Differential evolution-a sim-
ple and efficient adaptive scheme for global optimiza-
tion over continuous spaces, volume 3. ICSI Berkeley.
Storn, R. and Price, K. (1997). Differential evolution–a
simple and efficient heuristic for global optimization
over continuous spaces. Journal of global optimiza-
tion, 11(4):341–359.
Yang, X.-S. and Deb, S. (2009). Cuckoo search via l
´
evy
flights. In Nature & Biologically Inspired Computing,
2009. NaBIC 2009. World Congress on, pages 210–
214. IEEE.
Yang, X.-S. and Deb, S. (2010). Engineering optimi-
sation by cuckoo search. International Journal of
Mathematical Modelling and Numerical Optimisa-
tion, 1(4):330–343.
UnconstrainedGlobalOptimization:ABenchmarkComparisonofPopulation-basedAlgorithms
237
