
Robots Avoid Potential Failures through
Experience-based Probabilistic Planning
Melis Kapotoglu, Cagatay Koc and Sanem Sariel
Artificial Intelligence and Robotics Laboratory, Istanbul Technical University, Istanbul, Turkey
Keywords:
Learning-Guided Planning, Probabilistic Planning, Autonomous Robots, Mobile Manipulation.
Abstract:
Robots should avoid potential failure situations to safely execute their actions and to improve their perfor-
mances. For this purpose, they need to build and use their experience online. We propose online learning-
guided planning methods to address this problem. Our method includes an experiential learning process using
Inductive Logic Programming (ILP) and a probabilistic planning framework that uses the experience gained
by learning for improving task execution performance. We analyze our solution on a case study with an au-
tonomous mobile robot in a multi-object manipulation domain where the objective is maximizing the number
of collected objects while avoiding potential failures using experience. Our results indicate that the robot using
our adaptive planning strategy ensures safety in task execution and reduces the number of potential failures.
1 INTRODUCTION
Robots are expected to deal with uncertainties which
may depend on many factors like noisy sensory data,
lack of information or external events. These uncer-
tainties usually result in unpredictable states or un-
expected outcomes. Robots should detect these sit-
uations and deal with them. While one approach is
recovering from these cases, another approach is pre-
venting them before they occur. Prevention makes
prior experience on these cases necessary. The best
way is to let robots build their own experience and
use an adaptive planning/recovery strategy.
The main aim of this work is to develop an
experience-guided planning method that improves the
performance of a robot building its experience in run-
time. We particularly investigate multi-object manip-
ulation domain and focus on optimizing the number
of manipulated objects against failures. This can be
achieved by using the experience built from previous
failure cases on future planning tasks of the robot.
Our prior work involves an experiential learning pro-
cess (Karapinar et al., 2012; Karapinar and Sariel,
2015) using Inductive Logic Programming (ILP) and
a deterministic planner that uses the built experience
(Yildiz et al., 2013). The previous deterministic plan-
ner takes only the contexts of hypotheses into account
to provide feedback to the planning. The method
that we propose here extends our earlier study with
the development of a probabilistic planner framework
that makes use of probabilities of heuristics framed
by learning. The ILP-based learning process derives
hypotheses associated with probabilities and these hy-
potheses are then used to guide the planning process.
Our probabilistic framework uses a Partially Observ-
able Markov Decision Process (POMDP) model to
create an adaptive policy for the robot to deal with un-
certainties. In our case study, with the use of the prob-
abilistic planner, probabilistic hypotheses are used in
determining the order of preferences on objects for
manipulation, and the robot initially targets the ob-
jects that it believes to be successful in manipulating.
This paper is organized as follows. After re-
viewing previous studies on adaptive planning strate-
gies and POMDPs in Section II, background informa-
tion that describes POMDP framework is presented.
Experiential learning and POMDP-based guidance
methods are introduced in Section IV and Section V,
respectively. Finally, the experiment results are given
and discussed followed by the conclusions.
2 RELATED WORK
The main focus of this study is on experience-based
guidance methods for increasing efficiency by reduc-
ing potential failures. For this purpose, adaptive plan-
ning algorithms are used commonly to reduce or ex-
clude the possibility of failures.
111
Kapotoglu M., Koc C. and Sariel S..
Robots Avoid Potential Failures through Experience-based Probabilistic Planning.
DOI: 10.5220/0005548801110120
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 111-120
ISBN: 978-989-758-123-6
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Some studies (Pasula et al., 2004; Lang and Tous-
saint, 2010) aim to generate planning operators to im-
prove the performance of the robot. In (Pasula et al.,
2004), probabilistic STRIPS-like relational rules are
learned by extracting action dynamics that contain
preconditions, effects and probability distributions on
effects of actions. In this way, deterministic action
models are obtained to be used in the future as plan-
ning operators. Similarly in (Lang and Toussaint,
2010), probabilistic relational rules are generated and
used in planning. These systems use offline learn-
ing processes which means randomly generated train-
ing sets are used in their learning phases and their
systems’ performances are analyzed in simulations.
In our system, however, incrementally built experi-
ence gathered from real world experiments are used to
build the hypothesis space by the learning process. In
addition, guidance in probabilistic planning through
the use of these hypotheses is also performed in the
real world.
POMDPs have been investigated in many studies
for a wide variety of robotic tasks ranging from robot
navigation (Roy et al., 2006) to target tracking (Du
et al., 2010). To deal with the complexity of POMDPs
in these works, different approaches are presented
such as decreasing the number of uncertain variables
in the problem model (Png and Lee, 2009). Similar
to our domain, POMDPs are also used in robotic ma-
nipulation. In (Mons
´
o et al., 2012), manipulation task
of deformable objects with a robotic hand is modeled
with POMDPs to handle uncertainty in percepts and
actions. This work does not involve learning. In (Pa-
jarinen and Kyrki, 2014b) and (Pajarinen and Kyrki,
2014a), manipulation of multiple objects is selected
as the main challenge, and an online POMDP plan-
ning approach based on particle filtering is proposed
to change system dynamics according to action per-
formances. In that work, world state definitions con-
tain grasp success probabilities for objects. The prob-
abilities are updated after each grasping trial. Our
work differs from these works in the way we guide
the planning process with experience and applying a
generic method that can be applicable for all types of
actions in a planning domain without changing state
definitions.
3 BACKGROUND
We first review the POMDP formulation here for
convenience. Then, we present our POMDP frame-
work for learning-guided planning. POMDPs rep-
resent probabilistic processes that can be used to
devise plans for non-deterministic actions in par-
tially observable environments. A standard POMDP
framework for a robot is defined by the tuple
(S, A, O, T, Z, R, γ, b
0
). Here, S is the set of states
which contains all possible world states the robot
might be in, A is the set of actions that the robot
can execute, and O is the set of observations that can
be gathered through the sensors of the robot. Af-
ter executing action a ∈ A in state s ∈ S, the prob-
ability of reaching state s
0
∈ S in the next time step
is determined by the probabilistic transition model
T (s, a, s
0
) = P(s
0
|s, a). The transition probability de-
noted with P(s
0
|s, a) models non-deterministic out-
comes of actions. When transitioning to a new state
s
0
after executing action a, the probability of getting
the observation o ∈ O is also defined with a condi-
tional probability function Z(s
0
, a, o) = P(o|s
0
, a) as
the sensor model representing uncertainties in sens-
ing. R(s, a) function provides a real-valued immedi-
ate reward received after executing action a in state s.
The overall aim of the POMDP planning is to select
actions to maximize total reward as a cumulation of
immediate rewards during the execution of the plan.
A discount factor 0 ≤ γ ≤ 1 is set to bound the effects
of future rewards.
A belief state represents a world state that the
robot believes to be in and involves uncertainty due
to partial observability. Each belief state is associated
with a probability, and the robot decides on its next
action by evaluating all belief states it might exist in.
Before generating a plan, the initial probability dis-
tribution over belief states which is represented as b
0
should be determined. By using these components, a
policy which defines the best action for each state to
maximize the expected total reward is searched for.
Although both continuous and discrete represen-
tations of POMDPs exist in literature, discrete-state
POMDPs are commonly used in robotic domains to
reduce computational complexity. Otherwise, com-
plexity grows exponentially with the size of the state
space. One way to deal with complexity is using ap-
proximate methods such as point-based algorithms in
which belief states are sampled to obtain an approxi-
mate representation of the belief space. SARSOP is a
new point-based algorithm that improves the speed of
reaching a solution (Kurniawati et al., 2008). While
general point-based algorithms determine reachable
belief spaces, SARSOP deals with extracting opti-
mally reachable belief spaces. To achieve optimal-
ity, the algorithm exploits heuristic exploration while
sampling reachable belief states. We use the SARSOP
algorithm as a POMDP planner in our framework.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
112

4 EXPERIENCE-BASED
GUIDANCE
Our main objective in this study is to develop methods
for improving success rates in an autonomous robots’
task execution. Particularly, our case study involves
a mobile robot with an RGB-D sensor and a gripper
manipulating several objects scattered around.
4.1 Object Manipulation Case Study
In the investigated case study, the goal of our robot
is to transport as many objects as possible to its des-
tination in a given time period without any harm to
its environment. In the scenario, the robot selects the
order in which the objects are to be manipulated, and
moves these objects to their destinations. The robot
needs to determine which object to fetch next to max-
imize the number of objects transported without a fail-
ure. In this context, different optimization criteria can
be considered, such as choosing objects according to
their locations in order to minimize the distance trav-
elled or primarily targeting the objects on which the
robot has the best manipulation performance.
In our study, we let the robot initially build its ex-
perience by an experiential learning process to deter-
mine its abilities on object manipulation. Then, this
experience is used as a guidance for the robot’s next
decision. Hypotheses generated by the experiential
learning process can be used in planning to decide on
the next object to manipulate. Our previous study uses
a deterministic planner for this purpose, which uses
only contexts of hypotheses (Yildiz et al., 2013). In
this study, we propose to use a probabilistic planner
that can use probabilities of hypotheses as well.
In the case study, the robot starts its plan by first
finding the locations of the objects in the environment
(i.e., the object locations are not known apriori). If
it cannot detect or recognize any object in its current
field of view, it executes action search to find any ob-
ject by exploration. Whenever it finds an object, it
stops its movement and executes moveTo, pickU p,
transport actions in sequence, if there is no failure.
Whenever a failure is detected, the corresponding ob-
servation along with its related context is encoded in
the knowledge base (KB) of the robot. Supplemen-
tary sensing actions are also designed for detecting
failures occurring out of sensor range. For example,
for action pickU p, when the object is out of view
(i.e., when it is close to the robot), the RGB-D sen-
sor cannot detect it. If the robot senses that there is
a failure by its pressure sensors inside the gripper, it
moves backward to decide on whether the object is in
its original form, and another trial would be safe. If
the robot can not sense the object, an unknown failure
is assumed, and this observation is registered to the
KB.
We present the required processes for object
recognition/segmentation, scene interpretation, action
execution monitoring and learning in the following
subsections.
4.2 Scene Interpretation and Action
Execution Monitoring
Our system includes a Scene Interpreter to maintain a
consistent world model in the KB of the robot (Ozturk
et al., 2014). Information gathered from the environ-
ment by various sensors of the robot are processed
and fused before being stored into the KB. The con-
sistency is provided by integrating outputs from dif-
ferent vision methods. Template-based algorithms,
LINE-MOD (Hinterstoisser et al., 2012) and LINE-
MOD with HS histograms (Ersen et al., 2013), are
used for recognizing the objects. Moreover, unknown
objects are detected with a depth-based segmentation
method. The locations of the objects are determined
by fusing the outputs of these sources. In addition to
maintaining the consistency, Scene Interpreter applies
filtering on noisy data acquired through sensors. Fil-
tering process is performed by updating the informa-
tion maintained in the KB considering temporal and
domain-specific information during the evaluation of
new observations. Moreover, the appropriate sym-
bolic predicates that represent the world state are also
generated by Scene Interpreter (Ozturk et al., 2014).
The system also involves an Action Execution
Monitoring unit to detect different types of failures
that may happen during action execution of the robot.
This unit detects failures through observations and en-
codes their contextual information in the KB to build
the experience for use in future task executions. In
Action Execution Monitoring metric temporal formu-
las, defined specifically for each action, are used to
monitor the action execution simultaneously (Kapo-
toglu et al., 2014).
4.3 ILP Learning
We use Inductive Logic Programming (ILP) as an ex-
periential learning framework for autonomous robots
(Karapinar et al., 2012; Karapinar and Sariel, 2015).
Each detection of an action execution failure con-
tributes to derive hypotheses represented in first-order
logic and used to build the experience. The Progol
algorithm is used in ILP based-learning (Muggleton,
1995). The contexts of hypotheses are constructed
RobotsAvoidPotentialFailuresthroughExperience-basedProbabilisticPlanning
113

from the attributes of observed objects and the rele-
vant facts from the world state. Then, these contexts
are mapped to the outcomes (success or failure) of
corresponding actions. A probability (P) is attached
to each hypothesis. An example hypothesis is given in
Equation 1 where the probability of failure of action
pickU p for green cylindrical objects is determined as
0.22. The antecedent part of this rule is represented
as the context, and the conclusion is the outcome of
the action.
category(cylindrical) ∧color(green) ⇒
f ailure(pickU p)(P : 0.22)
(1)
The learning algorithm aims to find the most gen-
eral set of hypotheses by evaluating the gathered ob-
servations. The probability value of each hypothesis
is determined by calculating the ratio of positive ob-
servations corresponding to failure cases over all ob-
servations (negative and positive) covered by that hy-
pothesis. The derived hypotheses and their probabil-
ities are updated or ruled out while new observations
arrive. As an example, the learner is assumed to get
following observations:
obs
1
:
category(ob j
1
, bowlingPin)∧ color(ob j
1
, green) ∧
material(ob j
1
, plastic) ∧ size(ob j
1
, medium) ∧
f ailure(pickU p)
obs
2
:
category(ob j
2
, bowlingPin) ∧ color(ob j
2
, red) ∧
material(ob j
2
, plastic) ∧ size(ob j
2
, medium) ∧
f ailure(pickU p)
obs
3
:
category(ob j
3
, ball) ∧ color(ob j
3
, pur ple) ∧
material(ob j
3
, plastic) ∧ size(ob j
3
, medium) ∧
success(pickU p)
where obs
i
corresponds to an observation instance
taken after executing the action pickU p and ob j
i
cor-
responds to the object on which the action is executed.
After applying ILP learning on this observation set,
the following hypotheses are derived:
category(bowlingPin) ⇒ f ailure(pickU p)
category(ball) ⇒ success(pickU p)
Probabilities of these hypotheses are assigned
as 1 since there are no ambiguities. Furthermore,
the learning process can also benefit from back-
ground knowledge whenever it is available while de-
riving hypotheses. Unifications of hypotheses can
be performed more realistically by using background
knowledge. Therefore hypotheses can be generalized
effectively.
5 LEARNING-GUIDED
PROBABILISTIC PLANNING
The POMDP planning formulation for generating
policies in multi-object manipulation scenarios is
given in the following subsections.
5.1 State Space Definition (S)
An object composition, denoted as oc, represents a
structure that encapsulates qualitative and spatial in-
formation about an object. The i
th
object composition
formulated as oc
i
= (ob j
attr
j
, ob j
loc
m
j
, rel
loc
r
j
) contains
attributes and the semantic location of an object ob j
j
.
Since an object may be placed in all possible loca-
tions in the environment, more than one object com-
position exist for an object. Object attributes, denoted
as ob j
attr
j
, specify predetermined features (category,
color, material, height, width, etc.) of object ob j
j
.
Although the location of an object is valued in con-
tinuous space in the KB of the robot, the continuous-
valued locations are converted to semantic locations,
which are denoted as loc
m
for the m
th
semantic lo-
cation, to provide discretization in state definition of
POMDPs. Therefore, ob j
loc
m
j
indicates that the object
ob j
j
stands in location loc
m
. In addition to semantic
locations, one more field is attached into oc
i
, denoted
as rel
loc
r
j
, to represent the relative location of object
ob j
j
to the robot’s position loc
r
. In the current sys-
tem, only one spatial relation between an object and
the robot is defined as rel
loc
r
j
= {in f ront, ¬in f ront}.
The relation in f ront indicates that the mentioned ob-
ject stands in front of the robot. Since the robot moves
continuously in the environment, an object may situ-
ate in front of the robot according to the robot’s loca-
tion. This relation can be applied to at most one object
at any state.
For all combinations of object attributes and se-
mantic locations, different object compositions are
created. The set of all possible object compositions
is indicated as OC = {oc
1
, oc
2
, oc
3
, ...}. If the maxi-
mum number of object compositions that can exist in
the world at any moment is determined as N, a state
set of a POMDP that represents the current scene of
the world is given as follows where s
scene
is a subset
of OC:
S
scene
=
[
{s
scene
|s
scene
⊆ OC, |s
scene
| ≤ N}
State space of a POMDP S = S
scene
∪
{s
holding
, s
f ailure
} is formed as an aggregation of
various states. The state definition is expanded
with two more states, namely s
holding
and s
f ailure
.
Differently from state set S
scene
, each of these states
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
114

specifies only one condition. The state s
holding
repre-
sents that an object exists in the gripper of the robot
during transportation. The state s
f ailure
indicates
that a failure is encountered in the previous action
execution. The purpose of separating these states
from the state set S
scene
is to create an abstraction
from the other irrelevant state components in S
scene
.
This abstraction is also useful for reducing the
number of states generated by the POMDP.
5.2 Actions (A)
The actions considered in this work can be divided
into two groups according to their functionalities:
main actions and sensing actions. Main actions in
this formulation are moving to an object ob j
j
in
object composition oc
i
, instantiated for each oc
i
as
moveTo(oc
i
), picking up an object composition oc
i
,
denoted as pickU p(oc
i
) and putting the object in the
gripper down after reaching the destination, denoted
as transport. Action transport is executed as a com-
bined action that includes both transportation of the
object to the destination and putting the object down.
Note that this action is performed in the same way for
all objects held in the gripper, therefore a decision for
selecting an object to be transported, and correspond-
ingly an instantiation, is not needed. However, deci-
sions on object selection for moveTo and pickU p ac-
tions have an impact on task execution performance,
in terms of minimizing both time to complete and the
number of failures. This results in the need for instan-
tiations of moveTo and pickU p.
Sensing actions, denoted as search and monitor,
are executed for acquisition of knowledge about the
environment at any moment. The robot requires to
gather information from the environment when no
stored information exists in the KB. Action search is
the wandering operation to find new objects in these
situations. On the other hand, action monitor is ex-
ecuted when the information already available in the
KB needs to be updated. The robot senses the object
it currently operates on to verify the knowledge on the
situation of this object. Monitoring action is designed
as sensing the object on which the last main action is
operated, by the robot positioning itself to an appro-
priate location where it can see the object properly. In
this way, the knowledge of the robot about the object
is updated according to whether the object is sensed
again or not.
5.3 Transition Model (T )
The hypotheses generated by the experiential learn-
ing algorithm are to be used in the planning process
to decide on the next object to be manipulated. The
transition probabilities of pickU p(oc
i
) action to the
states which represent the success and failure of ac-
tion execution are specified using the probabilities at-
tached to the derived hypotheses. If an object compo-
sition is matched with the context of a hypothesis, the
corresponding pickU p failure probability is set to the
probability of the corresponding failure hypothesis. If
an object composition is in the scope of multiple hy-
potheses, the hypothesis with the lowest probability is
applied to avoid failures.
Transitions defined in the POMDP system, are
explained individually for each described action
in the following subsections. The state sets that
represent the preconditions and effects (excluding
failure cases) of each action are given symbolically
in Table 1. A failure case in execution of any action
cause a transition to state s
f ailure
.
Action moveTo Transitions.
Action moveTo(oc
i
) can be selected as the next action
if object composition oc
i
exists in the current belief of
the robot, and rel
loc
r
j
in oc
i
should be ¬in f ront before
executing moveTo(oc
i
) action as in this case execut-
ing an extra movement would be redundant. However,
there is no limitation about any other objects to be in
front of the robot, since the robot may decide on mov-
ing to a distant object instead of picking up the object
located in front. This decision is based on the eval-
uation of pickU p success performances regarding all
objects in the environment and their distances from
the robot. Since the selection of each action is deter-
mined by evaluating the total reward which indicates
the cumulative sum of the rewards of the current ac-
tion and the immediate rewards of all actions that may
come after this action, the robot decides to execute ei-
ther picking up the object in the front or moving to an-
other object with higher pickU p success performance
by considering future effects of these two actions.
Transition probabilities to the states that may
be encountered after the execution of action
moveTo(oc
i
), is determined according to the general
success performance of the moving operation of the
robot and the distance between the robot and the tar-
get object in oc
i
. The semantic locations of the objects
are defined by taking the starting position of the robot
as a reference.
After the execution of action moveTo(oc
i
), the
object in oc
i
is expected to be in front of the robot if
the action is successfully terminated. The information
about other objects found in the environment before
the execution of action moveTo(oc
i
) is updated with
a new observation taken after action execution. The
gathered observation is considered to be noisy and
RobotsAvoidPotentialFailuresthroughExperience-basedProbabilisticPlanning
115

Table 1: Symbolic representation of transition model.
Actions Start States Successful End States
moveTo(oc
i
) {s
scene
|oc
i
∈ s
scene
, (rel
loc
r
j
= ¬in f ront) for ob j
j
in oc
i
} {s
scene
|oc
i
∈ s
scene
, (rel
loc
r
j
= in f ront) for ob j
j
in oc
i
}
pickU p(oc
i
) {s
scene
|oc
i
∈ s
scene
, (rel
loc
r
j
= in f ront) for ob j
j
in oc
i
} {s
holding
}
transport {s
holding
} S
scene
search {|s
scene
| = 0} S
scene
monitor {s
f ailure
} S
scene
the object compositions of the next state after action
moveTo(oc
i
) is executed may stay the same or change
according to the incoming observation. The possibil-
ity of noise in the observation is considered for the
transitions to address unpredicted changes (e.g., the
existing objects in the environment may disappear by
external intervention) in scenes. Whenever a failure
is encountered in action execution, the next world
state becomes s
f ailure
.
Action pickU p Transitions.
The preconditions for action pickU p(oc
i
) include
that the robot’s gripper should be empty (i.e., any
state except s
holding
), and the object ob j
i
in oc
i
should be in front of the robot (rel
loc
r
j
). When this
action is successfully executed, the effect s
holding
occurs. If the robot discovers an action failure, the
state becomes s
f ailure
. Success probabilities for
these actions are determined based on the matchings
between the contexts of failure hypotheses and the
object composition.
Action transport Transitions.
The action transport entails the transportation of the
object in the gripper to the destination and putting
it down. Therefore, the precondition of this action
is holding an object (s
holding
). At the end of the
execution of this action, the robot is expected to put
down the object in hand to the destination. Transition
probabilities for passing to possible ending states
that have successful and failed action effects are
assigned empirically-determined values. The object
compositions in the environment after a successful
execution is determined with the new observation
and the transition probabilities to each successful
ending state are uniformly distributed. s
f ailure
cases
are handled in the same way as pickU p(oc
i
) and
moveTo(oc
i
) actions.
Action search Transitions.
If the robot is in the world state that does not have
any object composition, it searches the environment
in order to find new objects. After the execution of
search action, the robot may find itself in a world
state from the state set S
scene
. Since this is a sensing
action, the aim of which is to provide additional
world knowledge, this action does not have a success
or failure effect. Therefore, the probability is equally
distributed to the states in the state set S
scene
.
Action monitor Transitions.
When the robot encounters a failure during the execu-
tion of a main action, it transfers to the state s
f ailure
and needs to refresh its knowledge about the world.
In such cases, the action monitor is executed to pro-
vide additional information on the failure case. In our
system, the monitoring action is specified as moving
to a suitable position to sense the object on which the
last manipulation action is operated. After monitor-
ing, the belief state of the robot is updated and the
next action is determined according to this new be-
lief. After the execution of the action monitor, the
robot may find itself in a state with one of the com-
binations of object compositions. The next action is
determined by evaluating the current belief state of
the robot. Transition probabilities of monitor action
are uniformly distributed to all states in the state set
S
scene
.
5.4 Observation Model (Z)
Each observation gathered after an action execution
(i.e., after each transition between two world states) is
designed similar to the state definition. The observa-
tion model represents the probabilities of observations
gathered after a transition to a new state by executing
an action. In our work, each observation is encoded
into the KB by Scene Interpreter. The robot deter-
mines its belief state based on an observation which
is formulated identical to the state definition. Uncer-
tainties in sensing are handled by Scene Interpreter
and the output of this process is a set of observations
which reduces the complexity of POMDP planning.
5.5 Reward Model (R)
In our case study, the objective is to maximize the
number of objects to be transported by the robot. Re-
ducing failures is essential for this purpose, thus a
penalty is given when the robot is in state s
f ailure
. The
system is awarded if the intended transition to a new
state is achieved by a particular action. Sensing ac-
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
116

tions also cause the system to be penalized due to their
cost of execution.
6 EXPERIMENTS
Experiments were conducted in our department’s cor-
ridor without any special environmental lighting. We
also let people observe the experiments during which
their movements change illumination conditions. The
robot maintains its KB during runtime without any hu-
man intervention in the face of the challenges of noise
in sensory data, partial observability and unexpected
situations.
6.1 Experiment Setup
In order to evaluate the performance of our system,
we have conducted experiments with our Pioneer 3-
DX mobile robot. It is equipped with several sensors
to perceive its environment. A Hokuyo UTM-30LX
laser rangefinder is mounted on top of the robot facing
forward for mapping and localization, and an ASUS
Xtion PRO RGB-D camera is placed on top of the
laser rangefinder for 3D object recognition and seg-
mentation. The robot has a 2-DOF gripper to manip-
ulate objects.
The system is implemented on ROS (Robot Op-
erating System) framework (Quigley et al., 2009) us-
ing an Intel Core i7 laptop with Ubuntu 12.04 for au-
tonomous control of the robot.
6.2 POMDP System Parameters
In our case study, we take into account the following
object attributes: category (oc
category
i
), color (oc
color
i
),
material (oc
material
i
), size (width, oc
width
i
and height,
oc
height
i
), solidity (oc
solidity
i
) and shape (oc
shape
i
). Pos-
sible object compositions and their attributes are
given to the system as background information in the
experiments. Additionally, each object is assumed to
be unique and to exist only in a single location at any
time frame. Thus, a world state cannot have more than
one instance of a single object in the experiments.
However, the objects can be represented at different
locations at different world states. The semantic lo-
cations are assigned values proportional to their dis-
tances to the initial start position of the robot.
6.3 Scenarios
Initially, the performance of the robot is tested on a
set of five different objects from various colors and
Figure 1: The environment (Goal point of the robot is shown
with a red cross. room
1
and room
2
are denoted as blue and
yellow areas.)
categories: two plastic bowling pins whose colors are
green and red, a green plastic cylindrical object, a
small purple ball and a big red ball. The environment
is divided into two regions that represent the seman-
tic locations of objects. The robot, the objects and
the possible semantic locations, which can be denoted
as oc
loc
i
= (room
1
, room
2
), can be seen in Figure 1.
As preliminary experiments, the actions moveTo(oc
i
),
pickU p(oc
i
) and transport are executed ten times for
the object set randomly cluttered in the environment
to measure the overall performance of the robot on
multi-object manipulation tasks. It has been observed
in our preliminary experiments that the robot has an
overall pickU p success rate of 96%.
Two different scenarios are investigated to evalu-
ate the performance of the experience-based planning
system. Each scenario is repeated three times with
human injected failures. The occurrence times of
these failures are determined randomly based on the
selected failure probability distribution and applied
on the same order in both scenarios. The experiments
are performed with and without applying learning
outcomes to compare the results on the same failure
distribution. The experiments without learning do
not take the failure hypotheses into account, and the
robot proceeds to the objects in order based only on
their distances.
In the first scenario, objects with
category(bowlingPin) are externally taken away
from the environment with a predetermined prob-
ability (67%) at the time of action pickU p. For
this scenario, ILP generates the hypothesis given in
Equation 2.
category(bowlingPin) ⇒ f ailure(pickU p)
(P : 0.67)
(2)
The locations of bowling pins are organized in dif-
ferent settings as follows: both located in room
1
; one
of them in room
1
and the other one in room
2
; and both
of them in room
2
in different experiments. The sys-
tem’s performance is evaluated for all these cases.
RobotsAvoidPotentialFailuresthroughExperience-basedProbabilisticPlanning
117

Red Pin
Green Pin
Red Big Ball
Green Cylinder
Purple Ball
0s 60s 120s 180s 240s 300s 360s
move-to (mv) pick-up (p) transfer (t) monitor (mn) failure
p t
mv p t
mv p t
mv p mn mv p mn mv p t
mv p t
Figure 2: Timeline of the learning-guided plan execution with failures in bowling pins.
2
1
3
4
5
(a)
2
1
3
4
5
(b)
2
1
3
4
5
(c)
2
1
3
4
5
(d)
2
1
3
4
5
(e)
1
3
4
5
(f)
Figure 3: The graphical illustration of the execution for the first scenario. Objects are represented as circles which are
enumerated respectively for the green bowling pin, the purple ball, the red big ball, the green cylinder and the red bowling
pin. The blue region indicates the field of view of the robot where the objects can be recognized. The objects colored gray
indicate unseen objects. The circles with bold edges denote the objects with lower probability of pickU p success. The
recognized objects are shown in their respective colors.
The execution trace of the first scenario is given
in Figure 2 for the configuration given in Figure 1.
The graphical illustration of the first scenario is given
in Figure 3. The planning is guided with the failure
hypothesis given in Equation 2 for the first scenario.
The robot starts the execution of its plan without any
object in its KB, and it executes search action to find
an object in the environment (Figure 3(a)). Note that,
search action is not shown in Figure 2 due to clarity.
After search action, it detects the purple ball and the
green bowling pin located in room
1
(Figure 3(b)). Ac-
cording to the success probabilities of action pickU p
for different objects that are determined with expe-
rience, the robot selects the purple ball to move to,
since its pickU p success probability is higher (Fig-
ure 3(c)). The robot detects the objects that are lo-
cated in room
2
while moving to the purple ball. After
transporting the purple ball successfully (Figure 3(d)
and Figure 3(e)), the robot selects the cylindrical ob-
ject (in room
2
) with the higher success probability in-
stead of the closer bowling pin (Figure 3(f)). Then,
the big red ball is moved. Since the remaining ob-
jects (the green bowling pin and the red bowling pin)
in the environment have the same success probabil-
ity and there is no other alternative object, if there is
enough remaining time, the robot tries to manipulate
the closer one (green pin) first. According to the ran-
dom failure distributions, it is forced to fail two times
while picking these objects. It executes monitor ac-
tion to update the information after each failure.
0
1
2
3
4
5
6
7
8
9
10
11
1 2 3 4 5
Time[Minutes]
# of Succesfully Gathered Objects
Learning Guided Planning
Planning without Guidance
Action Failures
Figure 4: Time comparison between planning with and
without learning guidance in accordance with number of
successfully gathered objects
The results of time to complete another trial of
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
118
the first scneario with and without learning is given
as a histogram chart in Figure 4. Here, the number
of successfully transported objects is shown in rela-
tion to time. The red intervals in the histogram bars
indicate delays due to failures. The first failure is en-
countered earlier in the plan without guidance. The
planner without guidance chooses the closest object
to manipulate, since the success probabilities of all
the observed objects are believed to be equal. How-
ever, learning-guided planner manipulates the object
further away from the robot instead of the closer ob-
ject with lower success probability. The total required
time to manipulate all objects scattered in the environ-
ment are approximately the same. However, it is im-
portant to note that although the number of manipula-
tion trials in both executions are equivalent, learning-
guided planner postpones the manipulation of the ob-
jects with lower success probabilities until no other
objects are available. As can be seen from the figure,
when the robot uses experience, the potential failures
are postponed to a great extent. When the time per-
mits, the robot attempts to move towards objects for
which success is not guaranteed.
In the second scenario, the robot is forced to en-
counter failures by human intervention while manipu-
lating objects in room
1
. The objects are externally re-
moved while the robot is executing pickU p actions in
this location. The learning algorithm uses background
knowledge given in Equation 3 while extracting hy-
pothesis of the second scenario given in Equation 4
where ob j
i
represents an object, locX represents the x
coordinate of an object with respect to the global map
and location represents the semantic location of spec-
ified object. Although the objects in room
2
are further
away than the objects in room
1
, the planner selects the
objects in room
2
since the robot first attempts to trans-
port the objects with higher pickU p success probabil-
ities. However, in the experiments without learning,
the planner only takes into account the distances of
the objects.
locX(ob j
i
, X) ∧ 0 ≤ X < 1.6
⇒ location(ob j
i
, room
1
)
locX(ob j
i
, X) ∧ 1.6 ≤ X < 2.6
⇒ location(ob j
i
, room
2
)
(3)
location(ob j
i
, room
1
) ⇒ f ailure(pickU p)
(P : 0.67)
(4)
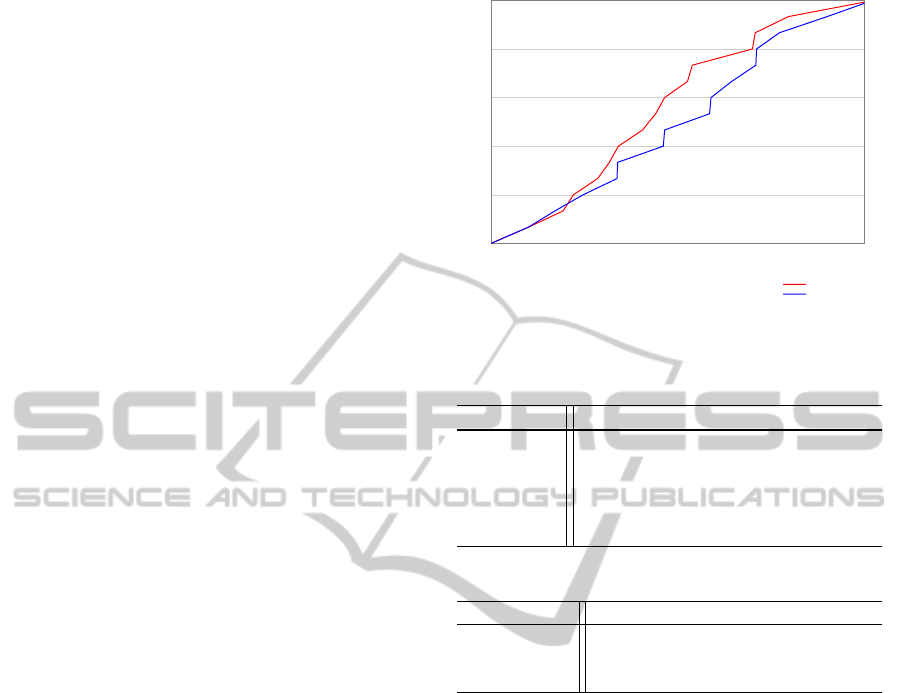
Figure 5 shows the average number of objects
transported over time with and without learning guid-
ance in the second scenario. This result shows that
when the probabilistic planner is fed with the learning
results, the number of transported objects is higher,
since the planner has the option of choosing the ob-
jects with higher success probabilities. However, after
all these objects are transported, the planner also sug-
gests transporting the remaining objects with lower
0
1
2
3
4
5
0 1 2 3 4 5 6 7 8 9
Average number of the collected objects
Time[minutes]
Pomdp Planner With Learning Probabilities Applied
Pomdp Planner Without Learning Probabilities Applied
Figure 5: The average number of objects transported
through time in the second scenario with failures in room
1
.
Table 2: Performance analysis vs. the number of objects.
#Objects #States #Actions Time(s)
1 7 7 0.18
2 23 11 0.54
3 83 15 2.62
4 299 19 11.94
5 1055 23 62.77
Table 3: Performance analysis vs. the number of locations.
#Locations #States #Actions Time(s)
1 50 11 0.58
2 299 19 11.94
3 1026 27 65.14
success probabilities. When the time period given
for the manipulation task is limited, the robot always
prefers to transport the objects with higher success
rates since it uses its experience. It should also be
noted that between time steps 1-2, although it seems
that POMDP without guidance gives better results,
this is due to a natural failure occurs. As the num-
ber of objects increase, we can see the advantage of
using experience.
We also analyze the performance of the planner
against the increasing number of objects and the num-
ber of locations in Table 2 and Table 3, respectively.
The columns present the number of states, the num-
ber of actions and the computation time. In Table 2,
the performance is analyzed for different number of
objects with two semantic locations. Table 3 presents
the results for four objects as the number of locations
changes. It can be seen that as the numbers of ob-
jects and locations increase, the numbers of gener-
ated states and actions increase as well. Thus, the
complexity and computation time of the planner in-
crease exponentially. This is one of the drawbacks of
POMDPs. However, this framework ensures that the
RobotsAvoidPotentialFailuresthroughExperience-basedProbabilisticPlanning
119

probabilistic hypotheses are used to guide planning
in a more realistic way which makes this framework
suitable for small-sized domains.
7 CONCLUSION
We presented our adaptive probabilistic planning
framework that uses the outputs of an experiential
learning process by an autonomous robot. Our case
study is on multi-object manipulation scenarios where
the robot’s objective is maximizing the cumulative
manipulation performance. The experiential learn-
ing process generates probabilistic hypotheses map-
ping from execution contexts to success or failure out-
comes in a learning-phase. The relevant object at-
tributes are represented in contexts of probabilistic
hypotheses which are fed to the probabilistic planning
framework to reduce the number of potential failures
in future plans. In this way, the robot decides on ac-
tions with higher probabilities of success by consider-
ing the gained experience. Our results show that the
probabilistic guidance in planning achieves the best
manipulation order of the objects within the knowl-
edge of the robot to maximize the transportation suc-
cess over time. In our future work, we aim to re-
duce the computational complexity by automatically
abstracting state representations in such domains.
ACKNOWLEDGEMENTS
This research is partly funded by a grant from the Sci-
entific and Technological Research Council of Turkey
(TUBITAK), Grant No. 111E-286. Authors thank
Melodi Deniz Ozturk, Dogan Altan, Sertac Karapinar
and Mustafa Ersen for their support.
REFERENCES
Du, Y., Hsu, D., Kurniawati, H., Lee, W., Ong, S., and Png,
S. (2010). A pomdp approach to robot motion plan-
ning under uncertainty. In Int. Conf. on Automated
Planning and Scheduling, Workshop on Solving Real-
World POMDP Problems.
Ersen, M., Talay, S. S., and Yalcin, H. (2013). Extracting
spatial relations among objects for failure detection.
In KIK@ KI, pages 13–20.
Hinterstoisser, S., Cagniart, C., Ilic, S., Sturm, P., Navab,
N., Fua, P., and Lepetit, V. (2012). Gradient re-
sponse maps for real-time detection of textureless ob-
jects. Pattern Analysis and Machine Intelligence,
IEEE Transactions on, 34(5):876–888.
Kapotoglu, M., Koc, C., Sariel, S., and Ince, G. (2014).
Action monitoring in cognitive robots. In Signal
Processing and Communications Applications Con-
ference (SIU), 2014 22nd, pages 2154–2157. IEEE.
Karapinar, S., Altan, D., and Sariel-Talay, S. (2012). A
robust planning framework for cognitive robots. In
Proceedings of the AAAI-12 Workshop on Cognitive
Robotics (CogRob).
Karapinar, S. and Sariel, S. (2015). Cognitive robots learn-
ing failure contexts through experimentation. In Pro-
ceedings of the 14th International Conference on Au-
tonomous Agents & Multiagent Systems.
Kurniawati, H., Hsu, D., and Lee, W. S. (2008). Sarsop: Ef-
ficient point-based pomdp planning by approximating
optimally reachable belief spaces. In Robotics: Sci-
ence and Systems, volume 2008. Zurich, Switzerland.
Lang, T. and Toussaint, M. (2010). Planning with noisy
probabilistic relational rules. Journal of Artificial In-
telligence Research, 39(1):1–49.
Mons
´
o, P., Aleny
`
a, G., and Torras, C. (2012). Pomdp ap-
proach to robotized clothes separation. In Intelligent
Robots and Systems (IROS), 2012 IEEE/RSJ Interna-
tional Conference on, pages 1324–1329. IEEE.
Muggleton, S. (1995). Inverse entailment and progol. New
generation computing, 13(3-4):245–286.
Ozturk, M. D., Ersen, M., Kapotoglu, M., Koc, C., Sariel-
Talay, S., and Yalcin, H. (2014). Scene interpre-
tation for self-aware cognitive robots. In AAAI-14
Spring Symposium on Qualitative Representations for
Robots.
Pajarinen, J. and Kyrki, V. (2014a). Robotic manipulation
in object composition space. In Intelligent Robots and
Systems (IROS 2014), 2014 IEEE/RSJ International
Conference on, pages 1–6. IEEE.
Pajarinen, J. and Kyrki, V. (2014b). Robotic manipula-
tion of multiple objects as a pomdp. arXiv preprint
arXiv:1402.0649.
Pasula, H., Zettlemoyer, L. S., and Kaelbling, L. P. (2004).
Learning probabilistic relational planning rules. In
ICAPS, pages 73–82.
Png, S. C. O. S. W. and Lee, D. H. W. S. (2009). Pomdps
for robotic tasks with mixed observability.
Quigley, M., Conley, K., Gerkey, B., Faust, J., Foote, T.,
Leibs, J., Wheeler, R., and Ng, A. Y. (2009). Ros: an
open-source robot operating system. In ICRA work-
shop on open source software, volume 3, page 5.
Roy, N., Gordon, G., and Thrun, S. (2006). Planning under
uncertainty for reliable health care robotics. In Field
and Service Robotics, pages 417–426. Springer.
Yildiz, P., Karapinar, S., and Sariel-Talay, S. (2013). Learn-
ing guided symbolic planning for cognitive robots. In
The IEEE International Conference on Robotics and
Automation (ICRA), Autonomous Learning Workshop.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
120
