Modeling Wine Preferences from Physicochemical Properties using

Fuzzy Techniques

Àngela Nebot

, Francisco Mugica

and Antoni Escobet

Soft Computing Research Group, Computer Science Dept., Universitat Politècnica de Catalunya - BarcelonaTech (UPC),

Jordi Girona Salgado 1-3, Barcelona, Spain

Soft Computing Research Group, DIPSE Dept., Universitat Politècnica de Catalunya - BarcelonaTech (UPC),

Campus Manresa, Avinguda de les Bases de Manresa, 61-73, 08240 Manresa, Spain

Keywords: Prediction, Wine Science, Fuzzy Inductive Reasoning (FIR), Genetic Fuzzy Systems, MOGUL.

Abstract: Wine classification is a difficult task since taste is the least understood of the human senses. In this research

we propose to use hybrid fuzzy logic techniques to predict human wine test preferences based on

physicochemical properties from wine analyses. Data obtained from Portuguese white wines are used in this

study. The fuzzy inductive reasoning technique achieved promising results, outperforming not only the

other fuzzy approaches studied but also other data mining techniques previously applied to the same dataset,

such are neural networks, support vector machines and multiple regression. Modeling wine preferences may

be useful not only for marketing purposes but also to improve wine production or support the oenologist

wine tasting evaluations.

1 INTRODUCTION

Data mining (DM) techniques aim at extracting

knowledge from raw data. Several DM algorithms

have been developed, each one with its own

advantages and disadvantages (Witten and Frank,

2005).

DM approaches have been applied to a large

variety of problems, either for classification or

regression. An interesting problem that has captured

the attention of several researches is the prediction

of wine quality (Cortez et al., 2009; Yin and Han,

2003).

Wine industry is investing in new technologies

for wine making and selling processes. A key issue

in this context is wine certification which prevents

the illegal adulteration and assures the wine quality.

Wine certification is often assessed by

physicochemical and sensory tests (Ebeler, 1999).

However, the relationships between the

physicochemical and sensory analysis are still not

fully understood (Legin et al., 2003).

That is the reason why DM techniques can be

very valuable to address this problem. The

development of an accurate, computationally

efficient and understandable prediction model can be

of great utility for the wine industry. On the one

hand, a good wine quality prediction can be very

useful in the certification phase, since currently the

sensory analysis is performed by human tasters,

being clearly a subjective approach. An automatic

predictive system can be integrated into a decision

support system, helping the speed and quality of the

oenologist performance. On the other hand, such a

prediction system can also be useful for training

oenology students or for marketing purposes.

Furthermore, a feature selection process can help

to analyze the impact of the analytical tests. If it is

concluded that several input variables are highly

relevant to predict the wine quality, since in the

production process some variables can be controlled,

this information can be used to improve the wine

quality.

In this paper wine taste preferences are modelled

by DM algorithms. In particular four hybrid fuzzy

techniques are proposed in this research. Three of

them are genetic fuzzy systems (GFS), which are

fuzzy systems that identify its structure and/or

parameters by means of genetic algorithms (GA)

and/or genetic programming (GP). The fourth

algorithm is the fuzzy inductive reasoning (FIR), a

hybridization of fuzzy and machine learning

approaches.

501

Nebot À., Mugica F. and Escobet A..

Modeling Wine Preferences from Physicochemical Properties using Fuzzy Techniques.

DOI: 10.5220/0005551905010507

In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),

pages 501-507

ISBN: 978-989-758-120-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

All the methodologies are studied in terms of

prediction accuracy as well as in terms of

computational effort. The results obtained by the

hybrid fuzzy techniques proposed are compared with

other DM techniques applied to the same problem in

previous studies (Cortez, 2009).

Section 2 presents the main concepts of the fuzzy

hybrid methodologies used in this research. In

section 3, the wine dataset available and the model

evaluation criteria used are described in detail. The

results are presented in section 4, where a

comparison with other DM methodologies is

performed. A discussion is also included in this

section in terms of results accuracy and

computational time needed for each approach.

Finally, the conclusions are presented in section 5.

2 METHODS

In this section the hybrid fuzzy methodologies

proposed are introduced. We propose hybrid

approaches instead of traditional fuzzy inference

systems since an optimization process is needed in

order to obtain the best fuzzy rules that represent the

behaviour of the system under study.

2.1 Fuzzy Inductive Reasoning (FIR)

The conceptualization of the FIR methodology

arises of the general system problem solving (GSPS)

approach proposed by Klir (Klir and Elias, 2002).

This methodology of modeling and simulation is

able to obtain good qualitative relations between the

variables that compose the system and to infer future

behavior of that system. It has the ability to describe

systems that cannot easily be described by classical

mathematics or statistics, i.e. systems for which the

underlying physical laws are not well understood.

FIR offers a model-based approach to

predicting either univariate or multi-variate time

series (Nebot et al., 2003; Carvajal and Nebot,

1998). A FIR model is a qualitative, non-

parametric, shallow model based on fuzzy logic.

Visual-FIR is a tool based on the FIR

methodology that offers a new perspective to the

modeling and simulation of complex systems.

Visual-FIR designs process blocks that allow the

treatment of the model identification and prediction

phases of FIR methodology in a compact, efficient

and user friendly manner (Escobet et al., 2008).

FIR methodology has two main processes: a

feature selection process, that allow to develop a

model, and the prediction or simulation process, that

uses the model obtained to infer the future behaviour

of the system.

A FIR model consists of its structure (relevant

variables) and a set of input/output relations (history

behavior) that are defined as if-then rules.

Feature selection in FIR is based on the

maximization of the models' forecasting power

quantified by a Shannon entropy-based quality

measure. The Shannon entropy measure is used to

determine the uncertainty associated with

forecasting a particular output state given any legal

input state. The overall entropy of the FIR model

structure studied, H

is computed as described in

equation 1.

()

HpiH









(1)

where p(i) is the probability of that input state to

occur and H

is the Shannon entropy relative to the

input state. Then, a normalized overall entropy H

is computed, as defined in equation 2.

max



(2)

is obviously a real-valued number in the range

between 0.0 and 1.0, where higher values indicate an

improved forecasting power. The model structure

with highest H

value generates forecasts with the

smallest amount of uncertainty.

Once the most relevant variables are identified,

they are used to derive the set of input/output

relations from the training data set, defined as a set

of if-then rules. This set of rules contains the

behaviour of the system. Using the k-nearest-

neighbours fuzzy inference algorithm the k rules

with the smallest distance measure are selected and a

distance-weighted average of their fuzzy

membership functions is computed and used to

forecast the fuzzy membership function of the

current state, as described in equation 3.

new j j

out rel out

emb w Memb







(3)

The weights

rel

are based on the distances and

are numbers between 0.0 and 1.0. Their sum is

always equal to 1.0. It is therefore possible to

interpret the relative weights as percentages.

For a more detailed explanation of the fuzzy

inductive reasoning methodology refer to (Escobet

et al., 2008).

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

502

2.2 Genetic-Fuzzy Systems

A Genetic Fuzzy System (GFS) is basically a fuzzy

system augmented by a learning process based on

evolutionary computation, which includes genetic

algorithms, genetic programming, and evolutionary

strategies, among other evolutionary algorithms

(Cordon et al., 2001). In this study three different

GFS are analyzed, i.e. MOGUL-TSK-R, MOGUL-

IRLHC-R and GFS-GPG-R.

MOGUL algorithms are based on the iterative

rule learning approach, where each chromosome in

the population represents a single fuzzy rule, but

only the best individual is considered to form part of

the final rule base. Therefore, it is run several times

to obtain the complete knowledge base. The

advantage is that it reduces substantially the search

space, because in each iteration only a fuzzy rule is

searched. A postprocessing stage is needed to force

the cooperation among the fuzzy rules generated in

the first stage.

2.2.1 MOGUL-TSK-R

MOGUL is a Methodology to Obtain Genetic fuzzy

rule-based systems Under the iterative rule Learning

approach. This methodology is composed of some

design guidelines that will allow us to obtain genetic

fuzzy rule base systems (GFRBS) to design different

types of fuzzy rule bases, i.e. descriptive and

approximate Mamdani-type and Sugeno-type.

The MOGUL-TSK-R is a MOGUL approach

base in the Sugeno type of rules (Alcalá et al., 2007).

In the first stage it performs a local identification of

prototypes to obtain a set of initial local semantics-

based Sugeno rules. On the other hand the

cooperation between rules is accomplished in the

second stage by means of a genetic niching-based

selection process to remove redundant rules and a

genetic tuning process to refine the fuzzy

parameters.

2.2.2 MOGUL- IRLHC-R

The MOGUL-IRLHC-R algorithm is also an

iterative rule learning approach that uses the

MOGUL paradigm, but in this case the goal is to

learn constrained approximate Mamdani-type

knowledge bases from examples (Cordón and

Herrera, 2001). It consists of three stages: an

evolutionary generation process, a genetic

multisimplification process and a genetic tuning

process. The first stage generates a set of fuzzy rules

with constrained free semantics covering the training

set in an adequate form. The second stage performs

a selection of rules using a binary coded genetic

algorithm with a genotypic sharing function and a

measure of the fuzzy rule base system performance.

The idea is to remove redundant rules while

maximizing the cooperation among the staying rules.

The third stage performs a tuning based on a real

coded genetic algorithm and the previous

performance measure. It adjusts the membership

functions of each rule in each possible fuzzy rule

base derived from the multisimplification process.

Then, the more accurate fuzzy rule based obtained is

the final output of the MOGUL-IRLHC-R

algorithm.

2.2.3 GFS-GPG-R

The GFS-GPG-R algorithm is a genetic fuzzy

system based on genetic programming grammar

operators (Sánchez et al., 2001). It combines genetic

programming operators with simulated annealing

search to solve symbolic regression problems.

The novelty of this approach is that a simulated

annealing-based method is designed for inducting

the crossover and mutation parameters and structure

of a fuzzy classifier. The adjacency operator in

simulated annealing is replaced with a

macromutation taken from tree-shaped genotype

genetic algorithms. The tree-shaped geneotypes

allow representing rule bases more compactly than

liniar representations.

3 METERIALS

3.1 Wine Data

The wine data used in this study comes from the

north-west region, named Minho, of Portugal, and

this dataset is available from the UCI machine

learning repository (UCI, 2015). It has been

proposed for both, regression and classification, by

Cortez et al. (2009). The white variant from the

mentioned demarcated region is analyzed as a

regression problem in this paper. The data were

collected from May 2004 to February 2007. This

dataset is much larger than others available as

benchmarks in the same domain.

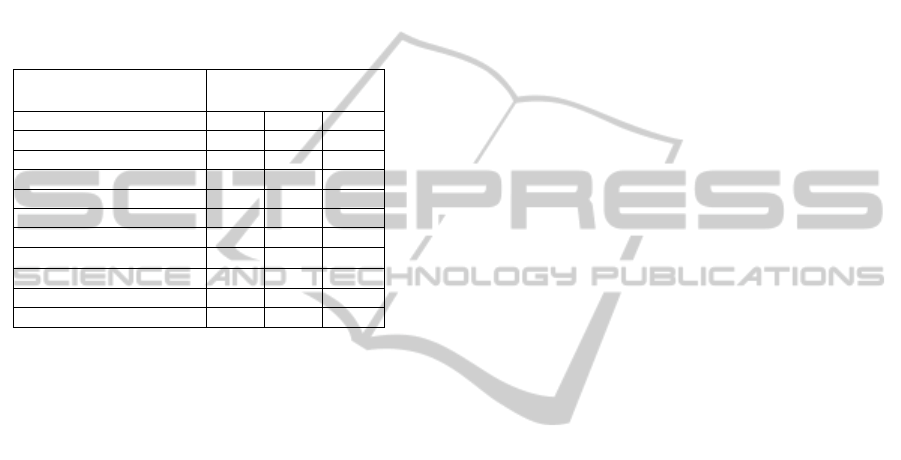
The more common physicochemical tests were

measured and are described in Table 1. These 11

properties are the inputs of the models.

Each one of the 4898 wine samples was

evaluated by a minimum of three sensory assessors,

by means of blind tastes, which graded the wine in

ModelingWinePreferencesfromPhysicochemicalPropertiesusingFuzzyTechniques

503

a scale that ranges from 0 to 10, that matches to

very bad to excellent quality, respectively. The

final score is given by the median of these

evaluations, which corresponds to the output

variable. This target variable denotes a typical

normal shape distribution, with minimum and

maximum values of 3 and 9 for the white wine.

Table 1: The physicochemical data (input variables), and

its corresponding statistics. The units are: FA: g(tartaric

acid)/dm

; VA: g(acetic acid)/dm

; CA: g/dm

; RS: g/dm

;

CH: g(sodium chloride)/dm

; FSD: mg/dm

; TSD: mg/dm

;

DE: g/dm

; SU: g(potassium sulphate)/dm

; AL: %vol.

Attribute White wine

Min Max Mean

Fixed acidity (FA) 3.8 14.2 6.9

Volatile acidity (VA) 0.1 1.1 0.3

Citric acid (CA) 0 1.7 0.3

Residual sugar (RS) 0.6 65.8 6.4

Chlorides (CH) 0.01 0.35 0.05

Free sulfur dioxide (FSD) 2 289 35

Total sulfur dioxide (TSD) 9 440 138

Density (DE)

0.987 1.039 0.994

pH 2.7 3.8 3.1

Sulphates (SU) 0.2 1.1 0.5

Alcohol (AL) 8 14.2 10.4

3.2 Model Evaluation

In order to test the generalization performance of the

fuzzy approaches studied in this research we use

cross validation, in this case 5-fold cross validation

(5-CV). The model parameters are derived using the

training subset and errors are computed using the

testing subset. For statistical confidence, the training

and testing processes are repeated 20 times with the

whole dataset randomly permuted in each run prior

to splitting in training and testing subsets.

The regression performance is commonly

measured by an error metric, such as the Mean

Absolute Deviation (MAD), described in equation

  

∑|















(4)

where ŷ

is the predicted output, y

the system output

and N the number of samples. Notice that the order

of the preferences is relevant, since a model that

predicts 5 when the real grade is 4 is better than a

model that predicts 6.

The regression error characteristic (REC) curve

is used very often to compare regression models,

with the ideal model presenting an area of 1.0. The

curve plots the absolute error tolerance T, versus the

percentage of points correctly predicted (accuracy)

within the tolerance.

The selection of the MAD and REC measures for

evaluation purposes allows us to compare the hybrid

fuzzy modeling methodologies presented in this

paper with the ones presented in (Cortez et al.,

2009), i.e. multilayer perceptron neural network,

support vector machine and multiple regression.

4 EXPERIMENTAL RESULTS

AND DISCUSSION

The Visual-FIR tool (Escobet et al., 2008) has been

used in this research to perform all the experiments

related to the FIR methodology. Visual-FIR is

developed under the matlab environment and

provides a GUI that allows the user to go through all

the processes of FIR methodology (refer to section

2.1) in a friendly manner and easy parameter

change.

On the other hand, the KEEL (Knowledge

Extraction based on Evolutionary Learning)

environment (Alcalá-Fdez et al., 2009, KEEL,

2005), has been used to perform all the experiments

related to GFS approaches. KEEL is an open source

Java software tool that can be used for a large

number of different knowledge data discovery tasks

and provides a simple GUI based on data flow to

design experiments.

All the experiments reported in this work were

conducted in a windows environment, with an Intel

dual core processor.

As explained before, to evaluate the selected

models, 20 runs have been preformed of the 5-fold

cross-validation, obtaining a total of 100

experiments for each model studied.

The first step in order to obtain the FIR models is

to discretize the data, i.e. to convert quantitative

values into fuzzy data. To this end, it becomes

necessary to define three parameters during the

discretization process, the number of classes (also

called granularity) chosen for each input and output

variable, the shape of their membership functions

and the discretization algorithm.

In this research it has been decided to discretize

all the input variables into two classes. The output

variable is discretized into seven classes, one for

each possible wine quality score, i.e. from 3 to 9.

A discretization of the input variables with more

than two classes can lead to a curse of

dimensionality problem. However, it was found that

two classes are enough for these variables to obtain

decent models.

A triangular shape has been used to represent the

membership functions associated to each class for all

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

504

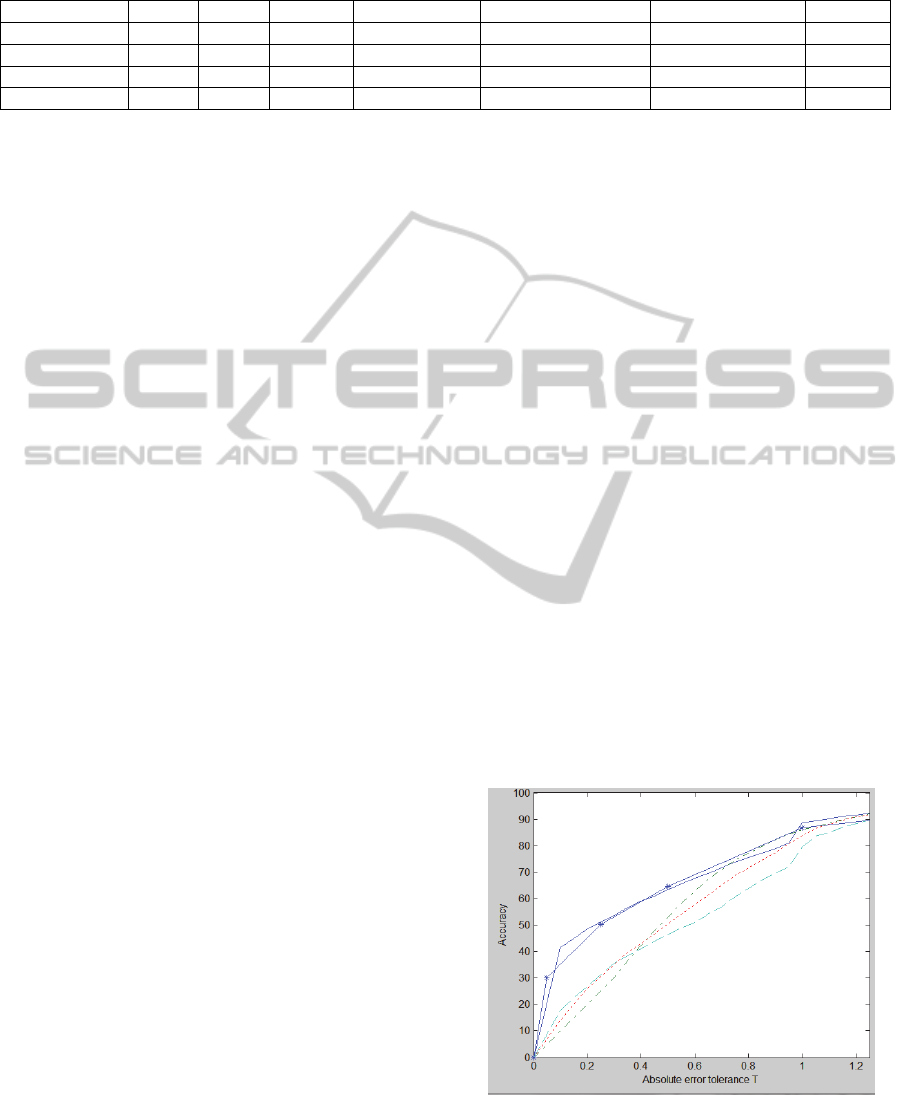
Table 2: The wine modeling results: MAD and Accuracy for three different tolerances. The values of MR, NN and SVM

columns are extracted from (Cortez et al., 2009).

MR NN SVM GFS-GPG-R MOGUL-IRLHC-R MOGUL-TSK-R FIR

MAD

0.59 0.58 0.45 0.63 0.58 0.56

0.44

Accuracy

T=0.25

25.6% 26.5% 50.3% 31.3% 30.6% 25.1%

51.2%

Accuracy

T=0.50

51.7% 52.6%

64.6%

46.3% 50.4% 53.0% 63.3%

Accuracy

T=1.00

84.3% 84.7% 86.8% 79.4% 83.8% 86.0%

88.7%

the variables involved in this study.

Depending on the algorithm chosen the

distribution of the membership functions in the

variable space may vary and this has a direct impact

to the reasoning process, and, therefore, to the model

predictions.

In this research, FIR uses the equal frequency

partition (EFP) algorithm for the discretization of the

input variables. The EFP algorithm distributes the

membership functions of a variable in such a way

that all the classes contain the same number of data

points.

Once the data has been discretized, FIR

methodology performs a feature selection process

where the more relevant causal relations between the

input variables and the output variable are identified.

To this end, we used the model structure

identification process of the fuzzy inductive

reasoning methodology that performs a feature

selection based on the entropy reduction measure as

described in section 2.1.

FIR founds that the features that have highest

relevant causal relation with the wine quality are:

alcohol, fixed acidity, free sulfur dioxide, residual

sugar and volatile acidity. Citric acid and sulphates

are also variables that have causal relation with the

wine quality but not with the same strength than the

previous ones. It can also be concluded that the total

sulfur dioxide is not a relevant variable to predict the

wine quality, presumably because it has redundant

information since the free sulfur dioxide is one of

the selected causal variables.

With respect the GFS algorithms studied, the

parameters by default are used (KEEL, 2005).

The results of all the experiments performed for

each tested configuration are summarized in Table 2.

Two metrics are presented, the MAD and the

classification accuracy for three different tolerances,

i.e. T=0.25, T=0.5 and T=1.0. In this domain a

tolerance of T = 1.0 is accepted as a good quality

control process.

The results obtained by Cortez et al. (2009) using

multiple regression (MR), multilayer perceptron

neural network (NN) and support vector machines

(SVM) are also included in the table for comparison

purposes.

The best results are shown in bold in Table 2.

For almost all the metrics, the FIR methodology is

the best choice. FIR obtains the lowest MAD error

and the highest accuracy for tolerances T = 0.25 and

T = 1.0. The SVM is the methodology that has the

second best results. It obtains, as FIR, a MAD error

lower than 0.5, the best T = 0.5 accuracy value and

better accuracy values for T = 0.25 and T = 1.0 than

the rest of the algorithms studied.

The two MOGUL algorithms perform in general

terms equally well than the MR and NN approaches.

The GFS-GPG-R is the fuzzy approach with poorest

results, however it has better accuracy for the 0.25

tolerance.

Figure 1 presents the REC curves of the 4 fuzzy

approaches studied in this research and the SVM.

It is clearly seen in Figure 1 that the differences

between the two best models, i.e. FIR and SVM, and

the rest of them are higher for small tolerances. For

T values lower than 0.4, the FIR and SVM

accuracies are almost two times better when

compared to the other fuzzy methods. For higher

tolerance values the accuracies become closer.

In terms of computational time effort, the

MOGUL algorithms are the most expensive,

followed by the SVM. FIR is the methodology that

obtains best results and uses less computational time

to obtain the system model and perform the

Figure 1: Average test set REC curves: FIR - solid line;

SVM - solid with star line; MOGUL-TSK-R - dashed with

dot line; MOGUL-IRLHC-R - doted line; GFS-GPG-R -

dashed line.

ModelingWinePreferencesfromPhysicochemicalPropertiesusingFuzzyTechniques

505

prediction. The execution time differences between

the methodologies analyzed, as expected, are really

big since the MOGUL approach performs a three

level optimization. While FIR needs around 10

minutes to perform a complete 5-CV prediction,

GFS-GPG-R about half an hour, SVM almost 2

hours and the MOGUL approaches need about 24

hours.

Encouraging results are achieved with the FIR

model providing the best performance,

outperforming the rest of the hybrid fuzzy

approaches studied. Moreover, the FIR results are

slightly better than the best ones obtained previously

for the same problem by Cortez et al. (2009), when

using SVM. An important advantage of FIR

methodology with respect SVMs is its reduced

computational time. FIR models are synthesized

rather than trained, allowing a quick modelling and

prediction computation. The difference in

computational time between FIR and SVM is

considerable, as stated before.

5 CONCLUSION

This work aims at the prediction of wine preferences

from physicochemical properties tests that are

available at the wine quality certification step. A

large dataset is accessible which contains white wine

samples from the northwest region of Portugal.

Four powerful hybrid fuzzy techniques that

perform data mining are studied in this research. In

the one hand the Fuzzy Inductive Reasoning (FIR)

methodology that is a non-parametric inductive

technique based on fuzzy logic and machine learning

approaches. On the other hand 3 different Genetic

Fuzzy Systems (GFS) that perform fuzzy rule

learning i.e. GFS-GPG-R, MOGUL-TSK-R and

MOGUL-IRLHC-R.

The GFS are much more computational

expensive than FIR since perform different

optimization levels using evolutionary algorithms.

On the other hand, FIR performs feature

selection during the modeling process, concluding

that the features that have highest relevant causal

relation with the wine quality are: alcohol, fixed

acidity, free sulfur dioxide, residual sugar and

volatile acidity. Citric acid and sulphates are also

variables that have causal relation with the wine

quality but not with the same strength than the

previous ones.

FIR, using the previously mentioned variables,

achieves the best performances, outperforming not

only the hybrid fuzzy techniques studied in this

article, but also other data mining methodologies

reported in other studies (Cortez et a., 2009), such

are Neural Networks (NN), Multiple Regression

(MR) and Support Vector Machines (SVM).

The results obtained using the SVM have very

similar error and accuracy metrics than the FIR

results. However, FIR has a great advantage over

SVM with respect the computational time.

As mentioned in all the studies that deal with

wine quality prediction, the results are really

relevant for different aspects of the wine industry.

On the one hand a good prediction can be very

useful in the certification phase. On the other hand,

such a prediction system can also be useful for

training oenology students or for marketing

purposes.

REFERENCES

Alcalá, R, Alcalá-Fdez. J., Casillas, J., Cordón, O.,

Herrera, F., 2007. Local identification of prototypes

for genetic learning of accurate TSK fuzzy rule-based

systems. International Journal of Intelligent Systems,

22, 909-941.

Alcalá-Fdez, J., Sánchez, L., García, S., del Jesus, M.J.,

Ventura, S., Garrell, J.M., Otero, J., Romero, C.,

Bacardit, J., Rivas, V.M., Fernández, J.C., Herrera, F.,

2009. KEEL: A Software Tool to Assess Evolutionary

Algorithms to Data Mining Problems. Soft Computing,

13:3, 307-318.

Carvajal, R., Nebot, A., 1998. Growth Model for White

Shrimp in Semi-intensive Farming using Inductive

Reasoning Methodology. Computers and Electronics

in Agriculture 19, 187-210.

Cordon, O., Herrera, F., 2001. Hybridizing genetic

algorithms with sharing scheme and evolution

strategies for designing approximate fuzzy rule-based

systems. Fuzzy sets and systems, 118, 235-255.

Cordon, O., Herrera, F., Hoffmann, F., Magdalena, L.,

2001. Genetic Fuzzy Systems. Evolutionary Tuning

and Learning of Fuzzy Knowledge Bases. Vol. 19 of

Advances in Fuzzy Systems - Applications and

Theory. World Scientific.

Cortez, P., Cerdeira, A., Almeida, F., Matos, T., Reis, J.,

2009. Modeling wine preferences by data mining from

physicochemical properties. In Decision Support

Systems, Elsevier, 47(4), 547-553.

Ebeler, S., 1999. Flavor Chemistry: Thirty Years of

Progress, Klumer Academic Publishers, 409-422.

Escobet, A., Nebot., A., Cellier, F.E., 2008. Visual-FIR: A

tool for model identification and prediction of

dynamical complex systems. Simulation Modelling

Practice and Theory 16, 76-92.

Keel Platform,2005. http://sci2s.ugr.es/keel/developpment.

php.

Klir, G., Elias, D., 2002. Architecture of Systems Problem

Solving, Plenum Press. New York, 2

edition.

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

506

Legin, A., Rudnitskaya, A., Lvova, L., Vlasov, Y., Di

Natale, C., D'Amico, A., 2003. Evaluation of Italian

wine by the electronic tongue: recognition,

quantitative analysis and correlation with human

sensory perception. Analytica Chimica Acta, 484(1), 7

May 2003, 33-44.

Nebot, A., Mugica, F., Cellier, F., Vallverdú, M., 2003.

Modeling and Simulation of the Central Nervous

System Control with Generic Fuzzy Models.

Simulation 79(11), 648-669.

Sánchez, L., Couso, I., Corrales, J.A., 2001. Combining

GP Operators with SA Search to Evolve Fuzzy Rule

Based Classifiers. Information Sciences, 136(1-4),

175-191.

UCI, 2015. http://archive.ics.uci.edu/ml/

Witten, I.H., Frank, E., 2005. Data Mining: Practical

Machine Learning Tools and Techniques with Java

Implementations. Morgan Kaufmann. Sant Francisco,

CA, 2nd Edition.

Yin, X., Han, J., 2003. CPAR: Classification based on

Predictive Association Rules. SDM , 3, 369-376.

ModelingWinePreferencesfromPhysicochemicalPropertiesusingFuzzyTechniques

507