
Comparative Analysis of Methods for the Log Boundaries Isolation
Artem V. Kruglov and Yuriy V. Chiryshev
Institute of Radioelectronics and Information Technologies, Ural State University named after the first
President of Russia B. N. Yeltsin, Mira st. 32, Yekaterinburg, Russian Federation
Keywords Image Processing, Boundary Detection, Hough Transform, Regression Analysis, Integral Projection.
Abstract The scrutiny of boundaries isolation methods is presented in this paper. The newly developed algorithms,
based on regression analysis and integral projection are compared with Hough transform in order to analyze
their effectiveness for the specific problem of moving logs control. The comparative analysis of the methods
was carried out on the database of images obtained from video sequence of real industrial process by the
criteria of accuracy and operation speed. Results of the test show that the line-by-line scanning method with
posterior LOWESS regression analysis has the best accuracy. However, the best appropriate for the
implementation in the real-time control systems based on machine vision technology is consecutive line
selection method due to its reasonable accuracy and impressive performance.
1 INTRODUCTION
The main objective of this scientific research is
development of real-time machine vision system
analyzing the geometry and wood type of logs
moving on conveyor belt. The procedure of analyzing
is a set of actions for the video sequence of logs. This
set includes selection of front-stage objects and a
description of their parameters for each frame, such as
the trajectory and velocity, and some attributes which
are specific for each task (developing system requires
the geometric characteristics of logs).
This work is devoted to the comparative analysis
of boundaries isolation algorithms as applied to
analyzed objects - logs. This task is complicated by
the fact that in the process of removing the bark from
the logs, some of it remains untidy, resulting in
significant distortion of the shape of the log. The
images of the log with bark remnants must be further
processed in order to restore the true edges of the log.
Analysis of the literature on the problem of
detection, isolation and determination of the
geometric parameters of objects via video
surveillance indicates that common methods and
algorithms (
Gonzalez, Woods, 2007) tend to be overly
complex and unsuitable for use in machine vision
systems operating in real time. Moreover, most
algorithms are suitable only for specific applications
and do not account for all possible situations that
could arise during the technological process of
logging, e.g. during transportation of logs on the
conveyor.
2 EASE OF USE
According to national standard of round timber
measurement methods – GOST R 52117-2003, there
are several methods for determining the volume of
log in Russia. Having regard to the possibility of
high-speed image processing with the use of machine
vision systems, the most accurate definition of timber
volume can be achieved with the sectional method.
The essence of the method is to calculate the volume
of the log (V, m
3
) as the sum of the volumes of
sections of truncated cones along the length of the
logs according to the formula:
()
1
22
1
22
3,1416
12 10000
3,1416 ( )
,
12 10000
n
i
iiii
i
nn n nn
l
VdDdD
ld DdD
−
=
⋅
=++⋅+
⋅
⋅⋅ + + ⋅
+
⋅
(1)
where l
i
– section lengths of a given size, m;
l
n
– last section of length n, having a length less
than l
i
, m;
d
i
, d
n
– the upper diameter of the common section
with given length and the one of the last, shorter
section, cm;
D
i
, D
n
– the lower diameter of the common
section with given length and the one of the, last,
shorter section, cm.
357
Kruglov A. and V. Chiryshev Y..
Comparative Analysis of Methods for the Log Boundaries Isolation.
DOI: 10.5220/0005552703570361
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 357-361
ISBN: 978-989-758-123-6
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

To isolate the boundaries of the log the following
procedure have been analyzed:
Hough method;
line-by-line image scanning method;
method of consecutive line selection.
2.1 Hough Method
In the context of the problem it is accepted that the
edge of the log could be approximated with sufficient
accuracy by a straight line or a piecewise linear
function. One of the most effective methods of
finding the straight lines on the image is Hough
transform (Fig. 1). This method is implemented with
the following guidelines (
Forsyth, Ponce, 2003):
Reducing the influence of the insignificant points.
Recommendation to reduce the influence of the noise
component is taken into account at the stage of log’s
edge detection by the gradient operator. Under the
assumption that the edges of logs orient mostly
vertically, Sobel operator with a mask "East" +
"West" was applied to accent boundaries. The result
of the edge detector implementation to the binary
image are shown on Fig. 1b.
Selection of the grid array. The choice of a large
grid pitch leads to the situation when the weight can
be mistakenly allocated to the cell which corresponds
to a number of different lines, and at small grid pitch
the weights of the points lying on the same line can be
in different cells. Based on the problem specification
and the existing image database the performance of
Hough method was analyzed at the different values of
grid pitch and threshold. The quality of the log edge
detection assessed visually. The best result was
achieved when the grid pitch value is 4 pixels, grid
pitch angle is π/18 and the threshold is 200.
The result of the algorithm implementation is
presented on the Fig. 1d.
Since the actual boundaries of the log may be
warped due to the knots, bark and trunk bend the
edges obtained by the edge detector are very noisy. It
was found that the Hough transformation is very
sensitive to the influence of distortion, which leads to
an erroneous allocation and even skipping edges or
finding several closely spaced lines with small
deviation angle (Fig. 1c). Furthermore, the quality of
the lines detection is also reduced in the case of the
log inclination.
2.2 Line-by-line Image Scanning
Method
To overcome the drawbacks of the Hough method, an
algorithm for log boundaries isolation through line-
by-line image scanning was developed. Assuming
that the target object is extended and rectilinear and
has vertical orientation, for each line of binary image
the search of x
_r
x
_l
points relating to the right and the
left boundary of the object respectively is
implemented. The search begins on conditions that
the weight of white dots corresponding to the width of
the observed object at the current line exceeds a
predetermined threshold. When the first required
point x
_i
is found its coordinates are stored in the
stack, and the analysis of a set of points x
_i+1
... x
_i+n
is
carried out. If they all belong to the front-stage object,
it is concluded that the observed object is a log, and
the point x
_i
- its boundary point for this line.
Otherwise, the stack is cleared and the boundary
search continues. As a result, after passing through all
lines of the image two sets M
_r
and M
_l
containing the
points of the right and left boundary of the log
respectively will be received:
_
=
,…,
;
_
=
л
,…,
л
(2)
where m - the number of lines in the image satisfying
the threshold condition by number of white dots.
The obtained set of points M
_r
and M
_l
describing log
boundaries may contain not only the points of the log
edges, but include elements of the sets belonging to
the edges of other objects, for example, bark or knots,
distorting the shape of the log. The following
approximation methods were used to exclude these
elements:
least-squares method;
algorithm LOWESS.
The essence of the ordinary least-squares method
(OLS) is to find the coefficients of the linear
dependence when (3) has the smallest value.
(
,
)
=(
−(
+))
(3)
where (
,
) are coordinates of the points of the set
M
_r
or M
_l
,
This model can be extended to the case of
polynomial approximation of higher power (k> 1).
Fig. 2a shows the selection of a third-power curve (k
= 3) for the one boundary of the log.
The evident advantage of the OLS method is low
computational complexity which means small
runtime. However, the method is quite sensitive to the
great single spikes associated with errors in the
identification and capturing of the data points. As is
known, the OLS algorithm based on the assumption
of independence and normality of the data
distribution.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
358
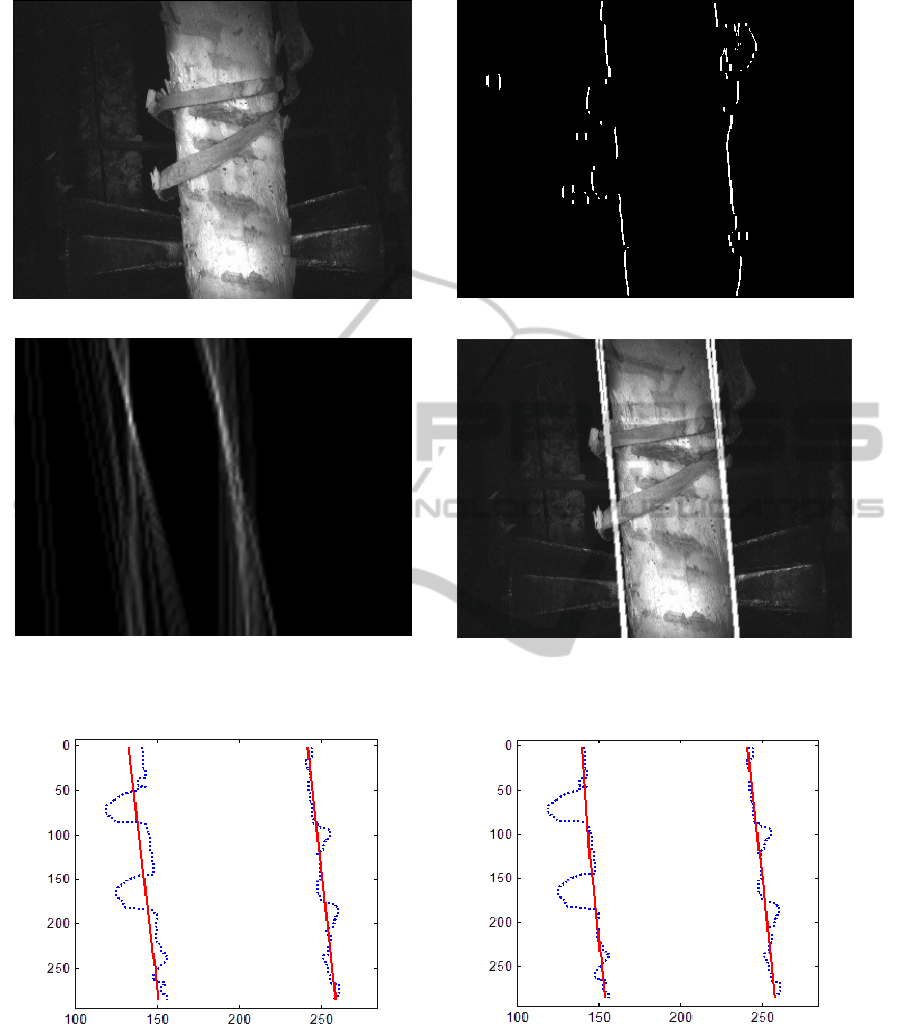
a)
b)
c)
d)
Figure 1: Illustration of Hough method. Origin image (a); image skeleton (b); Hough transform (c); final results of Hough
method (d).
a)
b)
Figure 2: Results of the implementation of the line-by-line image scanning method with OLS (a) and LOWESS (b)
approximation.
In this case, the assumption of normal distribution of
the data is incorrect because outliers of the sample
(points belonging to the bark or knots) are located
mainly on one side. As a result, there is a significant
departure of the approximating function from the true
value. Least-squares criterion assigns large weights to
the large objects and that is a serious problem in the
allocation of the log boundary.
In order to reduce the sensitivity to distortions the
method of robust nonparametric regression named
ComparativeAnalysisofMethodsfortheLogBoundariesIsolation
359

locally weighted smoothing (LOWESS) was used.
This technique was proposed for the simulation and
smoothing of two-dimensional data (Cleveland,
1979). The basic idea of the method is in the
assigning smaller weights to the sampling points with
a large deviation and building of the linear regression
on them. In other words, for a locally-linear model
LOWESS, which can be written in the form
=
+
+
,, we can show that the greater the error
=|
(
)
−
| , the more probably the point
(
,
) is outlier and its contribution to the final
regression model should be reduced. This is an
iterative operation, so the regression model is built
and robust weights are refined for each sampling
point at the each iteration until the weights become
stable (
Bendat, Piersol, 1993) (Fig. 2b).
Analyzing the results of applying the image scanning
method to isolate the boundaries of logs we can
conclude that:
for the OLS method approximating function is
shifted from the real boundaries of the log near
the minimum and maximum values of
("edge effect");
LOWESS algorithm cannot be used in the real
time systems due to high computational
complexity.
Thus, the above disadvantages of the image scanning
method hamper its implementation in real time
machine vision systems to the problem of logs
boundary detection.
2.3 Method of Consecutive Line
Selection
To overcome these drawbacks of the regression
analysis it is required to separate data points from
noise. The solution of this problem can be found by
the following algorithm, which results are presented
in Fig. 3:
the parameters of the observed object such as
position and angle of the boundary lines
trajectory are approximately determine on the
basis of the analysis of the horizontal
projection of the image;
then small pitch in angle and position relative
to the found trajectory the search of the line
which has the best approximation to the data
set of sample points is carried out. As a
criterion for consistency the majority principle
is used, i.e., line is considered as found if it is
consistent with the most part of the points.
Simulation of this algorithm gives the values of the
angle (3°) and shift (1 pixel) pitches that yield the best
results both in speed, and quality of the log
boundaries isolation.
Figure 3: Results of the consecutive line selection method.
3 TEST RESULTS
The described algorithms have been tested on the
image dataset obtained from the video of the real
technological process of the log passing down the
conveyor. Total amount of testing frames is about
800. The test PC has the following characteristics:
Intel Core i7 2.8 GHz, 4 Gb RAM and GeForce GTS
450. The results of the tests are given in the Table 1.
Table 1: Results of the algorithms testing.
Criterion
Hough
method
Line-by-line image
scanning method
Method of
consecutive
line selection
OLS LOWESS
Mean square
error, pix.
2,985 4,81 1,32 2,26
Maximum
error, pix.
6 8,96 2,76 3,57
Computational
complexity, ms
4-5 1 10-20 4-5
4 CONCLUSIONS
The tests show that the best result for the given real-
time image processing task has the method of
consecutive selection line. With the maximum error
in the 3.57 pixels., the performance of this method is
5 ms for an image format of 576*768 pixels. The line-
by-line image scanning method with robust
regression, despite smallest error among the
considered methods cannot be used in this problem
because of the critical runtime performance – 20 ms
for some cases, which is inappropriate for this
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
360

implementation. In the systems which are less time-
critical to the data processing, the most efficient use
of line-by-line image scanning method with
LOWESS robust regression.
REFERENCES
Rafael C. Gonzalez, Richard E. Woods, Digital image
processing, Prentice Hall, 3rd Edition, 2007.
David A. Forsyth, Jean Ponce, Computer Vision: A
Modern Approach, Prentice Hall, 2003.
Cleveland, W.S. “Robust Locally Weighted Regression
and Smoothing Scatterplots,” Journal of the American
Statistical Association, 1979.
Julius S. Bendat, Allan G. Piersol, Random Data: Analysis
and Measurement Procedures, Mathematics, 1993.
ComparativeAnalysisofMethodsfortheLogBoundariesIsolation
361
