
Optimizing Construction Sequences for Secant Pile Walls
Rong-Yau Huang, Ping-Fu Chen and Jieh-Haur Chen
Graduate Institute of Construction Engineering and Management, National Central University,
No. 300, Jhongda Rd., 32001, Jhongli District, Taoyuan City, Taiwan
Keywords: Pile Sequence, Optimization, Genetic Algorithm (GA).
Abstract: Secant pile walls are crucial in the construction of fossil-fuel power plants for water exclusion purposes.
The construction time is the most critical factor that influences the entire construction project. Thus,
shortening the time needed for building secant pile walls requires further investigation. Secant pile walls are
not required to be constructed in any particular order; typically, site engineers assign construction crews to
first build several primary bored piles, and then build secondary bored piles. However, building secant pile
walls in this sequence generally requires the primary bored piles to be excessively cured and hardened. The
construction of secondary bored piles in this manner thus results in construction difficulties, wasted
construction time, and poor construction quality. To address this practical problem, this study adopted a
genetic algorithm to investigate the optimal number of primary bored piles, the curing time, and the number
of daily working hours for the construction crew. In addition, the relationship between the curing time for
the primary bored piles and the construction time for the secondary bored piles was investigated by using a
case study, to ensure the overall research results corresponded to practical operation. The findings of this
study can facilitate the saving of construction time in the future construction of secant pile walls, enabling
the whole construction project to be completed successfully and improving public welfare.
1 INTRODUCTION
Construction time matters for activities. The
building of a secant pile wall requires the rental of
equipment and finding the optimal sequence to
minimize the construction time is one way to save
construction costs. Secant pile walls are necessary in
the fossil-fuel power plants construction project for
water exclusion purposes.
This research scope is
limited to finding the optimal construction sequence
of the work activities needed to build a secant pile
wall, which include grading, positioning of the site,
positioning of the equipment, driving the first 8-
meter casing into the ground, boring and cutting (0
–6 m),boring and cutting (6–12 m), driving the
second 8-meter casing into the ground, boring and
cutting (12–17 m), measuring the center of the pile,
measuring the altitude, ultrasound measurements,
placing of the steel cage, removal of bottom soil,
application of Bentonite slurry, pouring the concrete,
and removing the casing. Activities other than these
16 are not included. Such other activities could
include, for example, time for equipment
preparation, adjusting, relocating, and idle time.
Human effects such as the how the operator's skill
level and physical condition contribute to operations
are also excluded. In this study we try to develop an
effective and efficient model with Genetic
Algorithm to minimize the construction time. The
algorithm is applied to a case study to obtain the
optimal sequences for both primary and secondary
bored piles for a secant pile wall. Some factors
affect the total construction time are discussed with
sensitivity analysis, like the cement setting time of
the primary bored piles, the quantity of the primary
bored piles be done in a round and the working-
hour/ per day of the crew. The optimal sequences for
both primary and secondary bored piles are also
determined.
Previous studies on optimal solutions for
repetitive project scheduling have shown that when
problems are complex and large-scale, the efficiency
of analytical methods is considerably reduced;
determining optimal solutions may thus be hindered
by the excessively large amount of calculations and
time required (Al-Harbi et al., 1996). In the problem
of nonlinear optimization, the application of
analytical methods is typically difficult if not
impossible. A genetic algorithm (GA) is a direct
stochastic search technique that has been applied
widely in recent years. GA is used to determine
145
Huang R., Chen P. and Chen J..
Optimizing Construction Sequences for Secant Pile Walls.
DOI: 10.5220/0005553201450150
In Proceedings of the 10th International Conference on Software Engineering and Applications (ICSOFT-EA-2015), pages 145-150
ISBN: 978-989-758-114-4
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

optimal solutions based on the mechanism of natural
selection and the principle of survival-of-the-fittest.
GA generally yields satisfactory outcomes in a
relatively short amount of time. Therefore, this study
used the GA concept as basis to develop an
algorithm for optimizing the scheduling of a full-
casing secant pile wall.
2 PILE SEQUENCE
OPTIMIZATION MODEL
2.1 Model Assumption
To reduce the number of variables, the research
scope of this study was narrowed under several
assumptions, as follows:
(a) Construction crew (resource) = 1
Only one construction crew was assumed
to engage in the construction of the primary
and secondary bored piles, which were
assumed to be built at different times.
(b) Construction machinery (resource) = 1
Only one set of machines, including the
boring machine and spreader, were assumed in
the construction of the primary and secondary
bored piles. Every pile was assumed to be
constructed separately.
(c) The machinery transport time is excluded.
According to on-site observations, the time
required to transport machinery is
approximately 5 minutes. This was negligible
and consequently, the effect of transportation
time was not taken into account.
(d) The secondary bored piles were assumed to be
constructed after the primary bored piles were
constructed, in sequence.
The construction of primary bored piles is
affected by the geology of the area in which
they are being built. This study assumed that
the construction sequence for primary bored
piles did not influence the overall construction
time; only combinations to the construction
sequence for secondary bored piles were
considered.
(e) The drilling time for the secondary bored piles
is related to the curing time of the primary
bored piles.
Secant piles are composed of concrete, and
their curing time and strength is identical to that
of concrete generally. Increased curing time
results in increased curing strength, but the
strength plateaus after a specific time period.
(f) The secondary bored piles were assumed to be
constructed the day after all the primary bored
piles were built.
According to on-site observations, after the
construction of primary bored piles, the
construction site requires cleaning before
machinery for the construction of the secondary
bored piles can be brought in. Thus, the
construction of secondary bored piles is
generally initiated on the next day after the
construction of primary bored piles is
completed.
(g) The construction time was limited by the
working hours of the construction crew each
day.
If the construction time for the j
th
pile on the
i
th
day is T
ij
, then when ΣT
ij
is larger than the
construction time worked each day (T
k
), the
time spent on construction within one day is T
ij-
1
, and that of the next day is T
ij
.
(h) The time required to construct the secondary
bored piles was based on the curing time for
the preceding primary bored piles.
Because the construction of secondary bored
piles involves the drilling of primary bored piles to
form a watertight surface, the time required for
drilling is determined by the longest time needed to
cure the preceding primary bored pile. For example,
the time necessary to construct the sixth secondary
bored pile is based on the curing time for the fifth
secondary pile.
2.2 The Relationship Between the
Construction Time for Secondary
Bored Piles and the Curing Time
for Primary Bored Piles
Because of the properties of secant piles, the primary
bored piles must be established for a certain period
of time before pile driving of secondary bored piles
could be initiated, thereby achieving the goal of
water exclusion. However, no specifications for the
length of this waiting time are available. If the time
period is overly short, the concrete strength is
insufficient for construction processes. If the time
period is excessively long, the time spent on pile
driving may be considerable, or the machinery may
be damaged, resulting in extensions to the total
construction time. This study reviewed records of
the construction of primary and secondary bored
piles to understand the functional relationship
between the curing time for primary bored piles and
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
146
the construction time for secondary bored piles. This
relationship can then be used to estimate the
construction time needed for building secondary
bored piles. Based on 104 on-site records, the
maximum and minimum numbers of hours for the
construction of primary bored piles were obtained to
facilitate subsequent simulations, in which random
numbers corresponding to the uncertainties existing
in actual construction process were used. The
minimum number of hours required to construct
primary bored piles was 2.55, and the maximum was
4.55. Subsequently, regression analysis on the 104
on-site record data was performed to determine the
construction time for secondary bored piles, as
shown in Equation (1) and Fig. 1.
T
s
=-0.00009 T
p
2
+0.0362T
p
+2.9181 (1)
where T
s
denotes the construction time for the
secondary bored piles, and T
p
denotes the
construction time for the primary bored piles (the
longest construction time was selected).
Figure 1: The estimation of the time spent on constructing
secondary bored piles.
2.3 Development of the GA Model
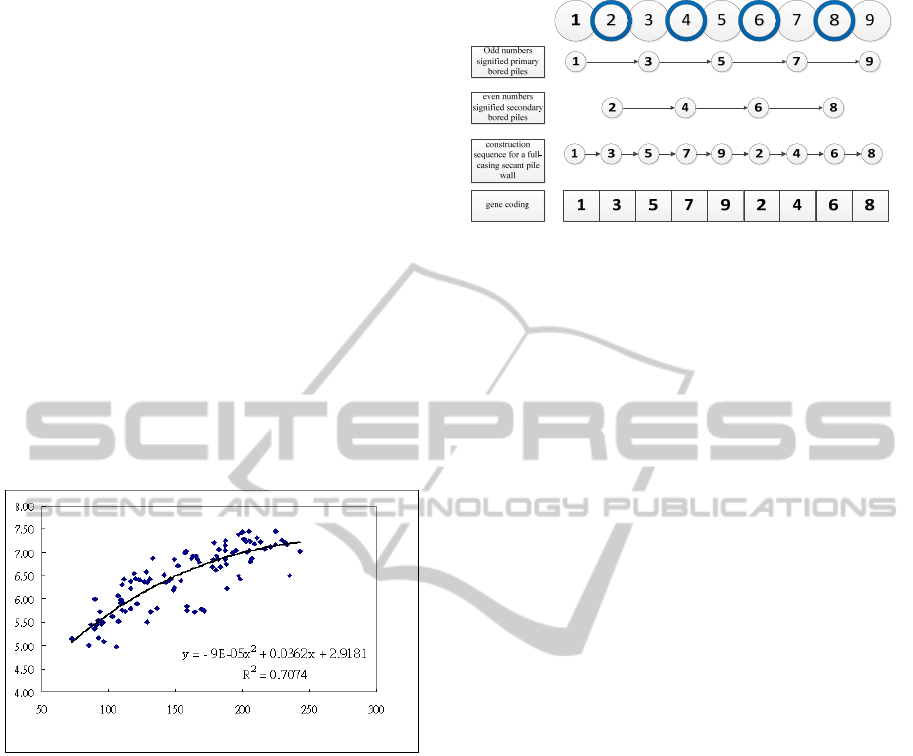
In the GA model developed in this study, piles were
numbered. Odd numbers signified primary bored
piles, and even numbers signified secondary bored
piles. Fig. 2 displays 5 primary bored piles and 4
secondary bored piles, or 9 units of full-casing
secant piles in total. Therefore, the chromosome
displayed in Fig. 2 indicates that the construction
sequence for a full-casing secant pile wall is
1→3→5→7→9→2→4→6→8.
Construction sequence for primary bored piles
Construction sequence for secondary bored
piles
Construction sequence for a full-casing secant
pile wall
Genetic codes
Figure 2: Construction sequence for secant piles and its
genetic representations.
(a) Production of parents: After the number of
primary bored piles (P) was input into the
model, random numbers were used to produce a
sequence (P-1) for the construction of secondary
bored piles.
(b) Crossover: One-point crossover was adopted.
(c) Mutation: Single-point mutation was conducted
in the model.
(d) Penalty function: The penalty function adopted
in this study was different from that commonly
used. Typically, a relatively extreme value is
used as a penalty function. For example, the
target value in this study was the total working
time consumption, which was a small value. A
total of 999 hours were allocated to a selected
pile that is not yet ready for pile construction.
Thus, the gene representative of that pile
becomes an undesired choice and has a low
possibility of being selected in the crossover
pool. However, this study adopted a deferred
penalty function. The produced parent
construction sequence was 2, 4, 6, 8, and 10,
and in other words, the second pile was the first
to be constructed. If the curing time for the
preceding first pile was shorter than the
minimum curing time, the second pile can only
be processed when the curing time (for the
preceding first pile) equaled the minimum
curing time. This waiting time was the deferred
penalty. Compared with the fixed penalty, the
deferred penalty allows the generation of
reasonable parent solutions.
(e) Selection: After the operation of the stated four
steps, the produced offspring T (the total time
consumption) was obtained by calculation. This
study adopted the roulette wheel selection,
where the roulette area was determined as 1/T,
which was used to select and retain the
offspring. Additionally, an elitist selection was
employed to retain superior combinations
among various generations and increase the
convergence speed.
OptimizingConstructionSequencesforSecantPileWalls
147

3 CASE STUDY
The case study involved the Siphon well
construction for circulating water in the Datan power
generation project, which is located in Datan
Village, Guanyin Township, Taoyuan County,
Taiwan. The parameters were set as follows:
(a) The number of primary bored piles: The number
of primary bored piles was denoted as N
p
, which
conformed to the principle of N
p
≧ 2 to enable
the construction of secondary bored piles. The
adopted numbers of primary bored piles in this
study were 5, 6, 7, 8, 9, 10, 15, 20, 25, and 30,
enabling the observation of variations in
construction times spent on various numbers of
primary bored piles.
(b) The construction time for the primary bored
piles: The construction time for the primary
bored piles was calculated based on the 104 on-
site construction data, from which the maximum
(4.55) and minimum (2.55) hours were
extracted. The system-produced time for
constructing primary bored piles (i.e.,T
p
) was
generated using random numbers; T
p
ranged
from 2.55 to 4.55.
(c) Number of working hours per day: The
construction crew’s working hours each day
were denoted as T
p
. Through interviews, this
study categorized the working times as 8 hours
(one-day work), 12 hours (one-day of work and
4 hours of overtime), 16 hours (shifts taken by
two construction crews), and 24 hours (shifts
taken by three construction crews, that is, the
full-day construction crews).
(d) The upper limit of the function: The upper limit
of the function was the condition for
terminating system operation. When the waiting
time exceeded the upper limit of the function,
the resulting sequence was regarded as
inadequate and would not be adopted
subsequently. In this study, the upper limit was
assumed to be 200 hours.
(e) The minimum curing time: At a construction
site, the time when the construction of the
secondary bored piles can be initiated (denoted
as T
a
) is generally based on a standard of seven
days. However, construction may also be
initiated after only three days of curing of
primary bored piles. In other words, the
standard curing time is not fixed. In this study,
various lengths of curing time were employed in
the analysis: 3 days (72 hours), 4 days (96
hours), 5 days (120 hours), and 7 days (168
hours).
The number of primary bored piles in a single
cycle: In one cycle, the number of constructed
primary bored piles may influence the time
consumption in that cycle and further influence the
total construction time. Accordingly, the quantities
of primary bored piles in one cycle were set as 6, 7,
8, 9, 10, 15, 20, 25, and 30 for the analysis, to
understand the required construction time when the
amounts of curing time were 72 hours, 96 hours, 120
hours, 144 hours, and 168 hours.
3.1 Analysis of Working Hours
per Day
The construction crew’s working hours each day
may influence the construction time of one cycle,
thereby influencing the total time consumed to
complete the entire construction project. Thus, the
quantity of primary bored piles in one cycle was set
as 5, 6, 7, 8, 9, 10, 15, 20, 25, and 30, and the curing
times were set as 72 hours, 96 hours, 120 hours, 144
hours, and 168 hours, for the subsequent analysis of
the working hours per day, which were 8 hours, 12
hours, 16 hours, and 24 hours.
The total amount of construction time was
influenced when the daily working hours were 12
and 16 hours. However, when the number of
working hours was 8 and 24 per day, the working
hours did not positively influence the total
construction time, because the required curing times
remained the same.
3.2 Sensitivity Analysis
The analysis in the previous section focused on a
single cycle. This study analysed three influencing
factors (the quantity of constructed primary and
secondary bored piles, the working hours per day,
and the curing time for the primary bored piles) and
employed the GA to optimize the construction
sequence for the secondary bored piles, yielding
satisfactory research outcomes. However, in
practice, a given project may need to construct a
fixed number of secant piles. In addition, the
working hours for each day and the possible curing
time are determined using cycle-number calculations
employed by previous studies. For example, in a
given project, 300 primary bored piles and 299
secondary bored piles must be completed. Assuming
that the curing time is 72 hours, working hours are 8
hours per day, and the number of primary bored
piles constructed in each cycle is 20, then the total
time consumption is calculated as follows:
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
148

Table 1: Curing time, quantities of primary bored piles, working hours per day, and the total amount of construction time.
Curing time Working hours/day
Number of piles
5 6 7 8 9 10 15 20 25 30
72 hr
8hr
10450.8
9911.0 9531.9 10144.9 9818.3 9556.5 10691.0 11258.3 10734.6 10625.5
12 hr 7871.4 7492.5 6665.6 6519.8 5988.3 5943.9 7331.0 7298.3 8142.6 8705.5
16 hr 7545.0 6555.0 6422.1 5628.4 5188.7 5217.0 4443.0 5138.3 5341.3 5171.1
24 hr 7014.6 6283.0 5621.1 5114.6 4715.7 4494.9 3593.4 3142.2
2958.4
3075.2
96 hr
8 hr
11904.6
11121.5 10565.6 10144.9 9818.3 9556.5 10691.0 11258.3 10734.6 10625.5
12 hr 9358.2 8709.0 8501.6 7432.1 7413.3 7395.6 7331.0 7658.3 8142.6 8945.5
16 hr 9370.8 8711.0 7728.9 7439.3 6822.3 6672.9 5540.6 5498.3 5341.3 5345.5
24 hr 8565.6 7502.0 6683.6 6061.5 5573.3 5225.1 4086.6 3521.7 3400.4
3316.6
120 hr
8hr 13351.8 12327.0 11595.0 11045.6 10618.3 10276.5 10691.0 11258.3 10734.6 10625.5
12 hr
13352.4
12327.5 11595.0 11045.6 10618.3 10276.5 9251.0 9098.3 9294.6 9425.5
16 hr 10842.0 9921.5 8777.1 8344.5 7633.0 7396.2 6022.2 5498.3 5341.3 5345.5
24 hr 10461.6 9030.0 7743.0 7002.4 6613.3 6143.4 5061.0 4418.3 3980.0
3731.1
144 hr
8 hr
14793.0
13527.5 12623.6 11945.6 11418.3 10996.5 10691.0 11258.3 10734.6 10625.5
12 hr 14793.0 13527.5 12623.6 11945.6 11418.3 10996.5 9731.0 9098.3 9294.6 9425.5
16 hr 12300.0 11127.0 9816.4 9245.6 8437.0 8116.5 6502.2 5858.3 5341.3 5345.5
24 hr 11910.6 10247.5 9057.4 8345.3 7635.0 7066.2 5542.2 4778.3 4268.0
3971.1
168 hr
8 hr
16233.0
14727.5 13652.1 12845.6 12218.3 11716.5 10691.0 11258.3 10734.6 10625.5
12 hr 16233.0 14727.5 13652.1 12845.6 12218.3 11716.5 10211.0 9458.3 9294.6 9425.5
16 hr 13746.6 12327.5 10847.6 10145.6 9237.0 8836.5 6982.2 6218.3 5629.3 5345.5
24 hr 13353.0 11782.0 10098.0 9245.6 8655.7 7790.1 6022.2 5138.3 4556.0
4211.1
Total time consumption = 300 (number of piles) / 20
(number of piles/cycle) * 750.55 (hours/cycle) =
11258.3 (hours)
Accordingly, this study investigated the total
time consumption under various standards of curing
time.
Assuming that the curing of concrete requires 72
hours, the total construction time is 10450.8 hours at
most and 2958.4 hours at least.
Assuming that the curing of concrete requires 96
hours, the total time consumption is 11904.6 hours
at most and 3316.6 hours at least.
Assuming that the curing of concrete requires
120 hours,the total construction time is 13352.4
hours at most and 3731.1 hours at least.
Assuming that the curing of concrete requires
144 hours, if the number of working hours is
between 8 hours and 24 hours per day, the total
construction time is 14793.0 hours at most and
3971.1 hours at least.
Assuming that the curing of concrete requires
168 hours, if the number of working hours is
between 8 hours and 24 hours per day, the total
construction time is 16233.0 hours at most and
4211.1 hours at least.
In sum, full-day construction requires the shortest
work duration. But the full-day crews may cost over
the budget of the project.
4 CONCLUSIONS
1. This study established an optimal construction
sequence model for secant pile walls. Regression
equations corresponding to various geological
conditions can be used for optimization
computations. Construction teams can reference
this method when determining the sequence of
secant pile wall construction.
2. A case study was conducted based on on-site
observations. Regression analysis was applied
according to the curing times for primary bored
piles and the drilling times for secondary bored
piles. The regression results indicated that the
two variables exhibited a strong correlation.
3. A close relationship was observed among the
working hours per day, the minimum curing
time, and the number of constructed piles. This
study conducted simulations on these three
variables in various combinations. Future studies
are recommended to focus on using these three
variables in simulations to determine the optimal
combinations of these variables, thereby
providing a reference for on-site construction
teams.
OptimizingConstructionSequencesforSecantPileWalls
149

ACKNOWLEDGEMENTS
This research is partially supported by the
“Developing a Simulation-Based Carbon Footprint
Assessment Model for Construction Operations” of
Ministry of Science and Technology, Taiwan,
R.O.C. under Grant no. MOST103-2221-E008-071-
MY2.
REFERENCES
Adeli, Hojjat, and Karim, Asim (1997), “Scheduling/cost
optimization and neural dynamics model for
construction”, J. of Constr. Engrg. and Mgmt., ASCE,
123(4), 450-458.
Al-Harbi, Kamal Al-Subhi, Selim, Shokri Z., and Al-
Sinan, Maazen (1996), “A multiobjective linear
program for scheduling repetitive projects”, Cost
Engrg., 38(12), 41-45.
Ammar, Mohammad A., and Elbeltagi, Emad (2001),
“Algorithm for determining controlling path
considering resource continuity”, J. Comp. in Civ.
Engrg., ASCE, 15(4), 292-298.
Chan, W. T., and Hu, Hao (2002), “Production Scheduling
for Precast Plants using a Flow Shop Sequencing
Model”, J. Comp. in Civ. Engrg.,ASCE, 16(3), 165-
174.
Dzeng, R. J., Tserng, H. P.,and Wang, W. C. (2005),
“Automating Schedule Review for Expressway
Construction”, J.of Constr. Engrg. and Mgmt.,ASCE,
131(1), 127-136.
Dzeng, R. J., Wang, W. C., and Tserng, H. P. (2004),
“Module-Based Construction Schedule Administration
for Public Infrastructure Agencies.” J.of
Constr.Engrg.and Mgmt., ASCE, 130(1), 5-14.
Feng, Chung-Wei, Cheng, Tao-Ming, and Wu, Hsien-
Tang (2004), “Optimizing the schedule of dispatching
RMC trucks through genetic algorithms”, Automation
in Construction, 13(3), 327–340.
Thomas, Randolph H., Oloufa Amr A, 「 Labor
Productivity, Disruption and Ripple Effect 」 , Cost
Engineering, Vol. 37, No.12, 1995.
Harris, Robert B. and Ioannou, Photios G. (1998),
“Scheduling projects with repeating activities”, J. of
Constr. Engrg .and Mgmt., ASCE, 124(4), 269-278.
Huang, Rong-Yau (2002), “Demand-supply model for
resource planning of repetitive construction projects”,
J.of Chinese institute of civil and hydraulic
engineering, 14(3), 551-559.
Leu, Sou-Sen, and Hwang, Shao-Ting (2002), “GA-based
resource-constrained flow-shop scheduling model for
mixed precast production”, Automation in
Construction, 11(4), 439-452.
Leu, Sou-Sen, and Hung, Tzung-Heng (2002), “A genetic
algorithm-based optimal resource-constrained
scheduling simulation model”, Construction
Management and Economics, 20(2), 131-141.
Leu, Sou-Sen, and Yang, Chung-Huei (1999), “GA-Based
Multicriteria Optimal Model for Construction
Scheduling”, J. of Constr. Engrg. and Mgmt., ASCE,
125(6), 420-427.
Mattila, Kris G, and Abraham, M. (1998), “Resource
leveling of linear schedules using integer linear
programming”, J. of Constr. Engrg. and Mgmt.,
ASCE, 124(3), 232-244.
Moselhi, Osama, and El-Rayes, Khaled (1993),
“Scheduling of repetitive projects with cost
optimization,” J. of constr. Engrg. and Mgmt. ASCE,
Vol. 119, No. 4, pp. 681-697.
Reeves, C. R. (1995), “A genetic algorithm for flowshop
sequencing”, Comp. and Operations Res., Oxford,
U.K., 22(1), 5–13.
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
150
