Preserving Prediction Accuracy on Incomplete Data Streams

Olivier Parisot, Yoanne Didry, Thomas Tamisier and Beno

ıt Otjacques

Luxembourg Institute of Science and Technology (LIST), Belvaux, Luxembourg

Keywords:

Data Streams, Model Trees, Missing Values Imputation.

Abstract:

Model tree is a useful and convenient method for predictive analytics in data streams, combining the inter-

pretability of decision trees with the efﬁciency of multiple linear regressions. However, missing values within

the data streams is a crucial issue in many real world applications. Often, this issue is solved by pre-processing

techniques applied prior to the training phase of the model. In this article we propose a new method that

proceeds by estimating and adjusting missing values before the model tree creation. A prototype has been

developed and experimental results on several benchmarks show that the method improves the accuracy of the

resulting model tree.

1 INTRODUCTION

Model trees are very convenient techniques to pre-

dict numerical values from past observations (Quin-

lan, 1992; Wang and Witten, 1996). Their popular-

ity is explained by the closeness with decision trees,

which uses an intuitive formalism understandable by

domain experts (Murthy, 1998). This aspect is crucial

as the model interpretability is critical in predictive

modeling (Shmueli and Koppius, 2011).

Given a data stream where each observation are

deﬁned by n features F

, . . . , F

, a model tree aims

at evaluating the value of a continuous feature F

ac-

cording to the values of the other features (F

, i 6= j).

A model tree is a directed graph composed of nodes,

branches and leaves (Figure 1). Each node is followed

by branches that specify a test on the feature value

(for instance: F

=value), and each leaf corresponds to

a multiple linear regression model that aims at com-

puting the value of the continuous class (Table 1).

A model tree can be built from static data by using

well-known induction algorithms like M5 (Quinlan,

1992). Recently, a streaming method has been pro-

posed to build model trees from evolving data streams

(Ikonomovska and Gama, 2008).

A model tree is characterized by two properties:

a) The complexity of a model tree can be measured by

its size (i.e. the number of nodes) (Breslow and Aha,

1997). In general, a big model tree is hard to visual-

ize and interpret (Stiglic et al., 2012). b) The accuracy

of a model tree is its ability to predict correct values,

i.e. the difference between predicted and expected

Figure 1: A simpliﬁed version of the model tree that pre-

dicts the quality of Portuguese Vinho Verde white wines by

using physicochemical data (Cortez et al., 2009): each leaf

corresponds to a multiple linear regression model (Table 1).

values. Traditionally, it can be estimated by consid-

ering the data as two parts (training set and evaluation

set). In the context of data streams, the accuracy has

to be measured iteratively for each observation of the

considered stream. To this end, various metrics exist

like the Mean Absolute Error (MAE) and Root Mean

Squared Error (RMSE).

Unfortunately, data quality is clearly an issue

when training a model tree from data streams, es-

pecially when data are incomplete (Zhu et al., 2008;

Fong and Yang, 2011). More precisely, as the model

tree learning can not deal with incomplete data di-

rectly, the data stream has to be preprocessed. More-

over, the imputation of these values has to be con-

trolled in order to have positive beneﬁt for further us-

Parisot O., Didry Y., Tamisier T. and Otjacques B..

Preserving Prediction Accuracy on Incomplete Data Streams.

DOI: 10.5220/0005553500910096

In Proceedings of 4th International Conference on Data Management Technologies and Applications (DATA-2015), pages 91-96

ISBN: 978-989-758-103-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Regression model for each leaf of the model tree that predicts the quality of Portuguese Vinho Verde white wines

(Figure 1). The estimated value is a numerical score between 0 and 10 (0 for a poor wine, 10 for an excellent wine).

Leaf Model to evaluate the quality of the wine.

LM1 -0.1122 * volatile acidity + 0 * free sulfur dioxide + 0.0049 * alcohol + 6.0006

LM2 -0.0788 * volatile acidity + 0 * free sulfur dioxide + 0.2372 * alcohol + 3.3594

LM3 -0.0442 * volatile acidity + 0.0003 * free sulfur dioxide + 0.0037 * alcohol + 5.047

LM4 -0.0442 * volatile acidity + 0.0001 * free sulfur dioxide + 0.0037 * alcohol + 5.3184

LM5 -0.0156 * volatile acidity + 0.0121 * free sulfur dioxide + 0.3269 * alcohol + 2.0913

age (Farhangfar et al., 2008).

To tackle this issue, we propose in this paper an

online method to adjust the missing values estima-

tion in such a way that it tends to increase the trained

model tree accuracy.

2 RELATED WORKS

Dealing with missing value is a well known topic

in data mining. To resolve this issue, data prepro-

cessing clearly helps to improve the performance of

learning algorithms (Zhu and Wu, 2004; Farhangfar

et al., 2008), and various methods have been proposed

(Marwala and Global, 2009; Van Buuren, 2012):

• Observations with missing data can be simply

deleted/ignored: this trivial approach can be sufﬁ-

cient in a lot of cases (Enders, 2010).

• Another simple solution consists in replacing

missing numerical values by the mean values, and

is still used in many statistical software packages.

However, this can highly disrupt the data structure

and so degrade the performance of the statistical

modeling (Junninen et al., 2004).

• Regression methods can be used for this task, es-

pecially when obvious relationships between the

attributes are known. In addition, regression trees

are good candidates too because they are efﬁcient

and easy to visualize/interpret (Kotsiantis, 2013).

• Artiﬁcial neural networks like perceptrons

(Tfwala et al., 2013) or Self Organized Map

(Mwale et al., 2012) have been recently used to

preprocess missing hydrological data.

However, processing data streams requires to ap-

ply time efﬁcient solutions. As a result, the classi-

cal imputation techniques can be applied on streams

by using a certain pool of observations (Zhu et al.,

2008). Furthermore, online methods can be used, for

example: decision trees for categorical missing values

(Domingos and Hulten, 2000) and regression trees for

numerical missing values (Ikonomovska et al., 2009).

3 CONTRIBUTION

During the training of a model tree from a data stream,

it is mandatory to apply a strategy to deal with ob-

servations with missing values, while controlling the

impact of this strategy on the learned model (Farhang-

far et al., 2008). In the next sections, we present two

naive approaches, and we propose a method that aims

at building a more accurate model tree.

3.1 Naive Approaches

The ﬁrst naive approach simply discards the observa-

tions with missing values (Alg. 1). This solution is

simple to apply but has a major drawback: if a lot of

data are missing from the stream - and it is frequent

in real-world cases (Fong and Yang, 2011), then the

model tree will be trained with few observations. In

addition, it creates a bias in predictive models if the

values are systematically missing in certain situations.

Algorithm 1: Skip the observations with missing values

before training the predictive model tree.

Require:

1: a data stream (DS)

Ensure:

2: modelTree ← initialize the model tree to be

trained using the data stream DS

3: while data stream DS not ﬁnished do

4: OBS ← get the next observation of the data

stream DS

5: if OBS does not contain missing values then

6: estimate error of modelTree for OBS

7: train modelTree with OBS

8: end if

9: end while

The second naive approach consists in ﬁlling in-

complete observations with estimated values before

training the model tree (Alg. 2). The imputation

method can be implemented with a set of data stream

prediction methods, for example: a) decision trees

for imputing categorical missing values (Domingos

DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications

and Hulten, 2000), b) or regression trees/model trees

for imputing numerical missing values (Ikonomovska

and Gama, 2008; Ikonomovska et al., 2009). Unfor-

tunately, this approach does not take into account the

impact of using these corrected data for the training

phase: in other words, they may lead without guaran-

tee to a more accurate/less accurate model tree.

Algorithm 2: Estimate the missing values before training

the predictive model tree.

Require:

1: a data stream (DS)

Ensure:

2: modelTree ← initialize the model tree to be

trained using the data stream DS

3: imputationMethod ← initialize an imputation

method for estimating missing values

4: while data stream DS not ﬁnished do

5: OBS ← get the next observation of the data

stream DS

6: if OBS contains missing values then

7: EST IM ←estimate the missing values of

OBS by using imputationMethod

8: OBS

←ﬁll OBS with EST IM

9: estimate error of modelTree for OBS

10: train modelTree with OBS

11: else

12: train imputationMethod with OBS

13: estimate error of modelTree for OBS

14: train modelTree with OBS

15: end if

16: end while

3.2 Our Adjusted Estimation Method

What are the effects of using estimated values to train

the model tree? In fact, it can impact the model tree

size (i.e. the interpretability) and the model tree ac-

curacy (i.e. the prediction error). In order to control

these aspects, we propose an approach to adjust the

estimated values for missing data in order to have a

positive impact on the learned model tree (Alg. 3).

Given a selected imputation method, the sug-

gested method aims at choosing a new estimation

for each missing value by using a range deﬁned

with: a) the value that is estimated by the imputa-

tion method. b) the current uncertainty / error of the

imputation method.

First of all, an initial model tree and an imputation

method are initialized (Alg. 3 - line 2,3). Then, while

the data stream is not ﬁnished (Alg. 3 - line 4), the

following steps are repeated:

• The next observation of the stream is considered

(Alg. 3 - line 5). If some values are missing from

the considered observation then:

– An estimation is computed for the missing

value by applying the imputation method (Alg.

3 - line 7).

– The conﬁdence level of the imputation method

is evaluated by the algorithm using the Mean

Absolute Error (Alg. 3 - line 8).

– By deﬁning a boundary with this conﬁdence

level , the algorithm tries different estimations

in such a way that the selected estimation will

have a low impact on the trained model tree

(Alg. 3 - line 9,10,11). This step is time-

efﬁcient, because it consists in simply selecting

the estimation which does not tend to increase

the model tree’s error-rate.

– The selected estimation is used to ﬁll the in-

complete observation (Alg. 3 - line 14). This

completed observation is used to train the

model tree (Alg. 3 - line 16).

• If the considered observation is complete then it

is used to train both the imputation method (Alg.

3 - line 18) and the model tree (Alg. 3 - line 20).

Progressively, by incrementally processing the

data stream, the algorithm aims at training the pre-

dictive model tree with adjusted estimations for the

incomplete data.

4 PROTOTYPE

In order to validate the approach described in this

paper, a prototype has been implemented as a JAVA

standalone tool. It is based on MOA (Bifet et al.,

2010), a widely-used data mining library for data

streams that provides algorithms for model tree induc-

tion. More precisely, it contains an implementation of

the FIMTDD algorithm (Ikonomovska et al., 2009).

Based on this prototype, we have evaluated our ap-

proach on various streams (Table 2). The data come

from the UCI Machine Learning repository (Bache

and Lichman, 2013), the Stream Data Mining Repos-

itory

and the Regression Datasets repository

To this end, these datasets have been considered

as streams, i.e. they have been iteratively processed

in an online way (in one pass). In each case: a) A

continuous class has been considered to build model

trees (Table 2). b) For a randomly selected attribute of

the stream, artiﬁcial missing values have been intro-

duced into 20% of observations, in order to check the

http://www.cse.fau.edu/ xqzhu/stream.html

http://www.dcc.fc.up.pt/∼ltorgo/

PreservingPredictionAccuracyonIncompleteDataStreams

Algorithm 3: Estimate and adjust the missing values before training the predictive model tree.

Require:

1: a data stream (DS)

Ensure:

2: modelTree ← initialize the model tree to be trained using the data stream DS

3: imputationMethod ← initialize an imputation method for estimating missing values

4: while data stream DS not ﬁnished do

5: OBS ← get the next observation of the data stream DS

6: if OBS contains missing values then

7: EST IM ←estimate the missing values of OBS by using imputationMethod

8: MAE ←evaluate the current Mean Absolute Error of imputationMethod

9: for VAL between [EST IM − MAE, EST IM + MAE] do

10: OBS

val

←ﬁll OBS with VAL

11: impact(VAL) ← measure the impact of training modelTree with OBS

val

12: end for

13: select VAL

best

for which impact(VAL

best

) is lower

14: OBS

←ﬁll OBS with VAL

best

15: estimate error of modelTree for OBS

16: train modelTree with OBS

17: else

18: train imputationMethod with OBS

19: estimate error of modelTree for OBS

20: train modelTree with OBS

21: end if

22: end while

imputation method (Table 2). c) 10% of the observa-

tions have been used to compute the prediction error

of the trained model tree (validation set). No missing

data have been introduced in this set.

The MOA’s implementation of the FIMTDD al-

gorithm has to be conﬁgured with several parame-

ters: splitConﬁdence and gracePeriod. Even if de-

fault values are provided by the implementation, we

have realized a empirical sensitivity analysis in or-

der to ﬁnd the best conﬁguration (i.e. leading to

a good tradeoff for the accuracy and the size of

the produced model tree): a) splitCon f idence = 0.1

b) gracePeriod = 200.

Then the different approaches to train the model

tree have been tested on these streams (Alg. 1,2,3). In

each case, the following metrics have been measured:

a) The size of the model trees after the training phase

(i.e. the count of nodes and leaves). b) The accuracy

of the model trees regarding the validation set (MAE

and RMSE). c) The conﬁdence level of the missing

value imputation (MAE and RMSE): it is obtained by

comparing the missing values estimation and the orig-

inal values of the stream (i.e. before removing values

from the data stream to generate artiﬁcial gaps).

After the experimentations, we can analyze the

model trees obtained with the different algorithms

(Tables 3,4,5). From these results, we can ob-

serve than skipping the incomplete observations (Alg.

1) leads to better results than learning observations

which are ﬁlled with the classical imputation method

(Alg. 2). For example, by considering the YearPre-

dictionMSD data stream, the ﬁrst one leads to a model

tree with RMSE = 10.55 and the second one leads to

a model tree with RMSE = 61.48. These results con-

ﬁrm that using an imputation method can have dra-

matic effects on the learned model tree.

Firstly, we can observe than our approach (Alg.

3) generally leads to more accurate model trees, in

comparison to those that are obtained by using the

other approaches (Alg. 1,2). For example, by con-

sidering the KDD Cup 99 data stream, the skipping

approach (Alg. 1) leads to a model tree with RMSE =

81.50 and the second one leads to a model tree with

RMSE = 63.45. We can note an exception for the

Forest Covertype data stream: the accuracy is exactly

the same for two approaches (RMSE = 0.12), but the

model tree size is smaller in the second case (5797

instead of 5805).

Secondly, our technique has a positive impact on

the model tree size too if we compare to the classical

imputation method (Alg. 2). But in general, skipping

the incomplete observations provides model trees that

are smaller than the other approaches.

Finally, if we compare our approach (Alg. 3) to

the classical imputation approach (Alg. 2), we can

see that the missing values imputation is positively

DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications

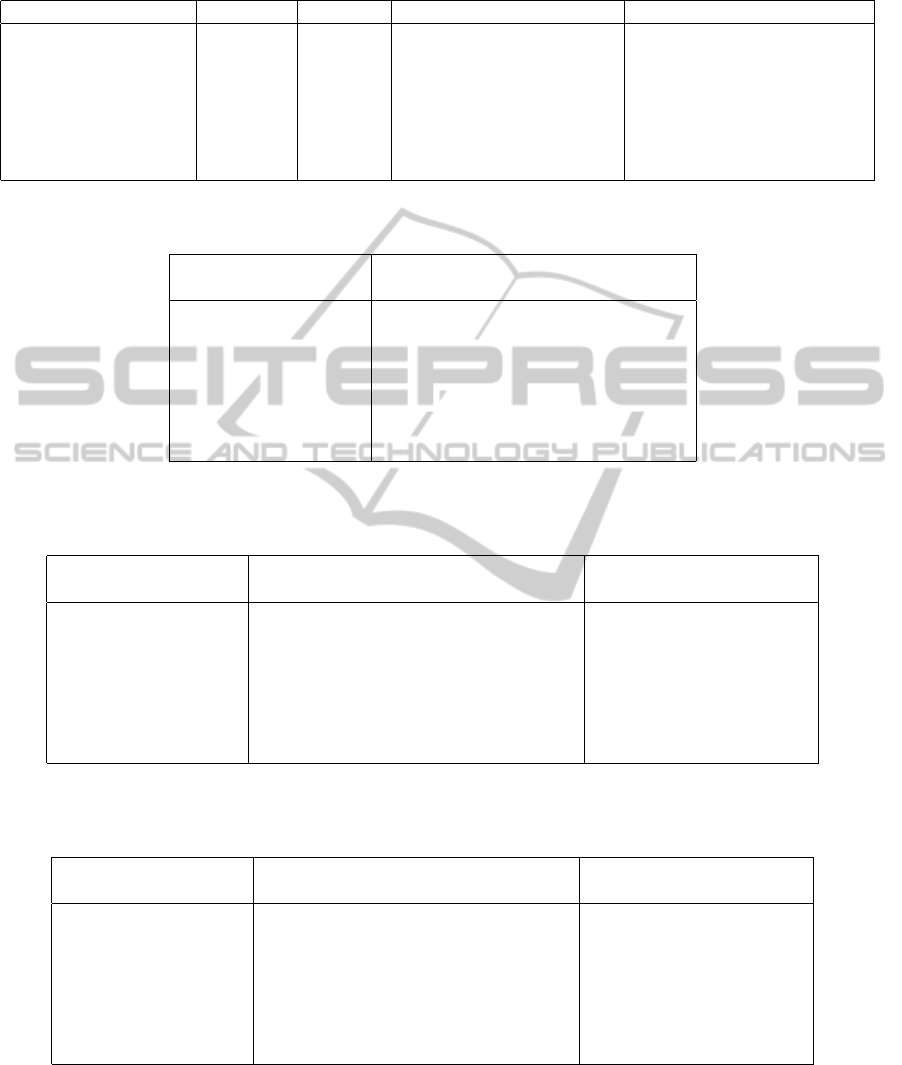
Table 2: The considered data streams and their characteristics. For each data stream, the considered continuous class to predict

with the model tree, and the attribute used to create artiﬁcial missing values.

Data stream #rows #features Continuous class to predict Attribute with missing values

MV Artiﬁcial Domain 40 768 11 y x10

Hyper Plane Stream 100 000 11 attribute1 attribute0

KDD Cup 99 145 585 42 dst host rerror rate dst host srv rerror rate

3D spatial network 434 874 4 altitude latitude

YearPredictionMSD 515 345 91 year attr11

Forest Covertype 581 012 55 aspect elevation

Sensor Stream 2 219 803 6 voltage humidity

Table 3: Results of the experiments with Algorithm 1. For each data stream, the size and the error rate of the trained model

tree are reported (MAE and RMSE are evaluated on the validation set, i.e. 10% of the values).

Data stream Trained model tree

Model tree size MAE RMSE

MV Artiﬁcial Domain 221 ± 1.28 ± 1.70

Hyper Plane Stream 475 ± 0.50 ± 0.58

KDD Cup 99 1 131 ± 0.75 ± 81.50

3D spatial network 3 403 ± 12.85 ± 16.33

YearPredictionMSD 4 091 ± 7.91 ± 10.55

Forest Covertype 4 641 ± 0.07 ± 0.12

Sensor Stream 17 737 ± 0.06 ± 0.14

Table 4: Results of the experiments with Algorithm 2. For each data stream, the size and the error rate of the trained model

tree are reported (MAE and RMSE are evaluated on the validation set, i.e. 10% of the values). Moreover, the error rates of

the missing values imputation are reported too (MAE and RMSE are evaluated on the fake missing data, i.e. 20% of data).

Data stream Trained model tree Missing values imputation

Model tree size MAE RMSE MAE RMSE

MV Artiﬁcial Domain 369 ± 26.87 ± 33.00 ± 51.14 ± 59.17

Hyper Plane Stream 661 ± 0.50 ± 0.58 ± 0.51 ± 0.59

KDD Cup 99 1 423 ± 1.01 ± 108.58 ± 0.14 ± 0.34

3D spatial network 4 273 ± 13.28 ± 16.72 ± 0.20 ± 0.23

YearPredictionMSD 5 123 ± 43.53 ± 61.48 ± 5.55 ± 7.30

Forest Covertype 5 797 ± 0.08 ± 0.12 ± 0.09 ± 0.14

Sensor Stream 22 177 ± 1.15 ± 1.52 ± 4.23 ± 15.40

Table 5: Results of the experiments with Algorithm 3. For each data stream, the size and the error rate of the trained model

tree are reported (MAE and RMSE are evaluated on the validation set, i.e. 10% of the values). Moreover, the error rates of

the missing values imputation are reported too (MAE and RMSE are evaluated on the fake missing data, i.e. 20% of data).

Data stream Trained model tree Missing values imputation

Model tree size MAE RMSE MAE RMSE

MV Artiﬁcial Domain 287 ± 1.21 ± 1.60 ± 14.46 ± 22.52

Hyper Plane Stream 637 ± 0.50 ± 0.58 ± 0.18 ± 0.34

KDD Cup 99 1 423 ± 0.60 ± 63.45 ± 0.14 ± 0.31

3D spatial network 4 273 ± 12.90 ± 16.36 ± 0.05 ± 0.10

YearPredictionMSD 5 123 ± 7.91 ± 10.55 ± 1.95 ± 4.05

Forest Covertype 5 805 ± 0.08 ± 0.12 ± 0.05 ± 0.09

Sensor Stream 22 177 ± 0.06 ± 0.14 ± 1.68 ± 14.80

impacted. For instance, if we consider Sensor Stream,

the conﬁdence level of the imputation is better by us-

ing our approach (RMSE = 14.8) than by using the

other one (RMSE = 15.4).

As a conclusion, our method helps to obtain more

accurate model trees by taking advantage of the miss-

ing values imputation process.

PreservingPredictionAccuracyonIncompleteDataStreams

5 CONCLUSION

In this paper, we presented a method to build predic-

tive model trees from data streams with incomplete

observations. The approach aims at adjusting the

missing values estimation in order to help the model

tree construction.

The method has been developed in a JAVA proto-

type, and its effectiveness was demonstrated and dis-

cussed on various data streams.

In future works, we will apply our method on

large real-world data streams related to e-commerce

and live sensors management. Moreover, we have in

view to improve the estimation method by using other

heuristics such as genetic algorithms.

ACKNOWLEDGEMENTS

The project is supported by a grant from the Min-

istry of Economy and External Trade, Grand-Duchy

of Luxembourg, under the RDI Law.

Moreover, this work has been realized in partner-

ship with the inﬁnAIt Solutions S.A. company (

so we would like to thank Gero Vierke and Helmut

Rieder for their help.

REFERENCES

Bache, K. and Lichman, M. (2013). UCI M.L. repository.

Bifet, A., Holmes, G., Kirkby, R., and Pfahringer, B.

(2010). Moa: Massive online analysis. The Journal of

Machine Learning Research, 11:1601–1604.

Breslow, L. A. and Aha, D. W. (1997). Simplifying decision

trees: A survey. Knowl. Eng. Rev., 12(1):1–40.

Cortez, P., Cerdeira, A., Almeida, F., Matos, T., and Reis,

J. (2009). Modeling wine preferences by data mining

from physicochemical properties. Decision Support

Systems, 47(4):547 – 553. Smart Business Networks:

Concepts and Empirical Evidence.

Domingos, P. and Hulten, G. (2000). Mining high-speed

data streams. In Proceedings of the sixth ACM

SIGKDD international conference on Knowledge dis-

covery and data mining, pages 71–80. ACM.

Enders, C. K. (2010). Applied missing data analysis. Guil-

ford Publications.

Farhangfar, A., Kurgan, L., and Dy, J. (2008). Impact of

imputation of missing values on classiﬁcation error for

discrete data. Pattern Recognit., 41(12):3692–3705.

Fong, S. and Yang, H. (2011). The six technical gaps be-

tween intelligent applications and real-time data min-

ing: A critical review. Journal of Emerging Technolo-

gies in Web Intelligence, 3(2).

http://inﬁnait.eu

Ikonomovska, E. and Gama, J. (2008). Learning model

trees from data streams. In Discovery Science, pages

52–63. Springer.

Ikonomovska, E., Gama, J., Sebasti

ao, R., and Gjorgjevik,

D. (2009). Regression trees from data streams with

drift detection. In Discovery Science, pages 121–135.

Junninen, H., Niska, H., Tuppurainen, K., Ruuskanen, J.,

and Kolehmainen, M. (2004). Methods for imputation

of missing values in air quality data sets. Atmospheric

Environment, 38(18):2895 – 2907.

Kotsiantis, S. (2013). Decision trees: a recent overview.

Artiﬁcial Intelligence Review, 39(4):261–283.

Marwala, T. and Global, I. (2009). Computational intel-

ligence for missing data imputation, estimation and

management: knowledge optimization techniques. In-

formation Science Reference Herhsey, USA.

Murthy, S. K. (1998). Automatic construction of decision

trees from data: A multi-disciplinary survey. Data

Min. Knowl. Discov., 2(4):345–389.

Mwale, F., Adeloye, A., and Rustum, R. (2012). Inﬁlling of

missing rainfall and streamﬂow data in the Shire River

basin, Malawi–a SOM approach. Phys. and Chem. of

the Earth, 50:34–43.

Quinlan, J. R. (1992). Learning with continuous classes.

In 5th Australian joint Conference on Artiﬁcial Intel-

ligence, volume 92, pages 343–348. Singapore.

Shmueli, G. and Koppius, O. R. (2011). Predictive analyt-

ics in information systems research. Mis Quarterly,

35(3):553–572.

Stiglic, G., Kocbek, S., Pernek, I., and Kokol, P. (2012).

Comprehensive decision tree models in bioinformat-

ics. PLoS ONE, 7(3):e33812.

Tfwala, S. S., Wang, Y.-M., and Lin, Y.-C. (2013). Predic-

tion of missing ﬂow records using multilayer percep-

tron and coactive neurofuzzy inference system. The

Sc. World Journal, 2013.

Van Buuren, S. (2012). Flexible imputation of missing data.

CRC press.

Wang, Y. and Witten, I. H. (1996). Induction of model trees

for predicting continuous classes.

Zhu, X. and Wu, X. (2004). Class noise vs. attribute noise:

A quantitative study. A. I. Review, 22(3):177–210.

Zhu, X., Zhang, P., Wu, X., He, D., Zhang, C., and Shi, Y.

(2008). Cleansing noisy data streams. In ICDM 08,

pages 1139–1144. IEEE.

DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications