
Automatic Generation of Concept Maps based on Collection of
Teaching Materials
Aliya Nugumanova
1
, Madina Mansurova
2
, Ermek Alimzhanov
2
, Dmitry Zyryanov
1
and Kurmash Apayev
1
1
D. Serikbayev East Kazakhstan State Technical University, Oskemen, Kazakhstan
2
al-Farabi Kazakh National University, Almaty, Kazakhstan
Keywords: Concept Map, Co-occurrence Analysis, Term-term Matrix, Term-document Matrix, Chi-squared Test.
Abstract: The aim of this work is demonstration of usefulness and efficiency of statistical methods of text processing
for automatic construction of concept maps of the pre-determined domain. Statistical methods considered in
this paper are based on the analysis of co-occurrence of terms in the domain documents. To perform such
analysis, at the first step we construct a term-document frequency matrix on the basis of which we can
estimate the correlation between terms and the designed domain. At the second step we go on from the
term-document matrix to the term-term matrix that allows to estimate the correlation between pairs of terms.
The use of such approach allows to define the links between concepts as links in pairs which have the
highest values of correlation. At the third step, we have to summarize the obtained information identifying
concepts as nodes and links as edges of a graph and construct a concept map as resulting graph.
1 INTRODUCTION
Concept maps or semantic maps are a means of
visualization of subject knowledge. The main figures
of concept maps are concepts (key notions of the
domain) put in circles or boxes. Concepts can be
connected with each other by relations represented
in the form of lines. The relations can be signed by
words or word combinations expressing their
purpose and meaning. In the broad sense, concept
maps can be treated as visual means of presenting
ontologies and thesauri of domains. However, their
main purpose is to contribute to a deeper
understanding of the subject and allow to represent
the structure of the subject knowledge on the
conceptual level.
The work (Sherman, 2003) reports the results of
experimental investigations verifying the practical
value and efficiency of using concept maps as a
strategy of teaching. Unfortunately, the complexity
of a manual construction of the concept maps greatly
reduces the advantages of their using in the
educational process. As a result, when preparing
courses studies, teachers often renounce the use of
concept maps or have to simplify their
representation decreasing the number of concepts in
the map or designating only the clearest and the
most important relations between concepts.
Owing to the mentioned arguments, of special
importance is the task of automatic or semi-
automatic construction of concept maps on the basis
of their extraction from a collection of text
documents. Following the authors of (Villalon et.al,
2008) example this task got the name Concept Map
Mining (CMM) similar to Data Mining (retrieval of
useful information from large data files) and Text
Mining (retrieval of useful information from large
text arrays). In general case the process of CMM
consists of three subtasks: extraction of concepts,
extraction of links and summarization (Villalon et.al,
2010) (see Figure 1).
Figure 1: The subtasks of concept map mining process.
The aim of this work is demonstration of
usefulness and efficiency of statistical methods of
text processing for automatic construction of
concept maps of the pre-determined domain. One of
the most important virtues of statistical techniques is
248
Nugumanova A., Mansurova M., Alimzhanov E., Zyryanov D. and Apayev K..
Automatic Generation of Concept Maps based on Collection of Teaching Materials.
DOI: 10.5220/0005554702480254
In Proceedings of 4th International Conference on Data Management Technologies and Applications (DATA-2015), pages 248-254
ISBN: 978-989-758-103-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

that they can be directly applied to any domain and
any language, i.e. they are invariant in regard to the
most important attributes of teaching courses, such
as the field of knowledge and language of teaching.
Statistical methods considered in this paper are
based on the analysis of co-occurrence of terms in
the domain documents. To perform such analysis, at
the first step we construct a term-document
frequency matrix on the basis of which we can
estimate the correlation between terms and the
designed domain. We suppose that the more often a
certain term occurs in the documents of the given
subject domain and the sparser in the documents of
other themes, the closer it is to the given domain, i.e.
the higher is the correlation between the term and
the domain. The use of such approach allows us to
define concepts as terms which have a high level of
correlation with the domain documents. At the
second step we go on from the term-document
matrix to the term-term matrix that allows to
estimate the correlation not between terms and
documents but between pairs of terms. The use of
such approach allows to define the links between
concepts as links in pairs which have the highest
values of correlation. Thus, we have a concrete two-
step algorithm for extraction of concepts and links
between them. At the third step, we have to
summarize the obtained information identifying
concepts as nodes and links as edges of a graph and
construct a resulting graph (see Figure 2).
Figure 2: Proposed realization of concept map mining
process.
Automatically created concept maps we plan to
integrate in e-learning environments as a learning
activity aimed to student’s active and deep learning
of the subject. In (Akhmed-Zaki et al., 2014) we
represent our conception of such e-learning
environment, and in this paper we investigate one of
its meaningful elements.
The remaining part of the work has the following
structure. The second section presents a brief review
of works related to the considered problem of
automatic construction of concept maps. The
approach proposed in this work is described in detail
in the third section. The results of experimental
testing of the proposed approach are given in the
fourth section. The fifth section contains brief
conclusions on the work done and presents a plan of
further investigations.
2 RELATED WORKS
The resent decade is characterized by the growth of
interest to investigations devoted to automatic
extraction of concept maps from collections of text
materials. Among these investigations, of high rank
are the works based on the use of statistical
techniques of processing a natural language. As is
mentioned in (Zubrinic et al., 2012), the methods
focused on statistical processing of texts are simple,
efficient and well portable, however, they possess a
decreased accuracy as they do not consider latent
semantics in the text.
The mentioned simplicity and efficiency of
statistical approaches are illustrated well in (Clariana
et al., 2004). The authors construct a term-term
matrix based on a short list of key words selected
manually for the considered domain. They fill in the
matrix on the basis of terms co-occurrence in
sentences. If two elements occur in on sentence, the
matrix element is equated to 1, otherwise – to 0.
Then they display this matrix in the concept map, as
shown in Figure 3. Obviously, such approach is
good for chamber teaching courses consisting of
materials limited in volume. For weighty courses
such approach is very inefficient.
Figure 3: Mapping the term-term matrix to the concept
map.
These authors applied their methodology for
constructing concept maps based on students’ text
summaries. The obtained concept maps were used
by instructor to analyze how students learned the
training material. In particular, the purpose of the
analysis was selection of correct, incorrect or
missing propositions in the students’ summaries.
AutomaticGenerationofConceptMapsbasedonCollectionofTeachingMaterials
249
The authors of (Chen et al., 2008) extract
concepts from scientific articles using the principal
component analysis. For the extracted concepts they
introduce the notion “relation strength” with the help
of which they describe correlation between two
concepts calculated on the basis of distance between
these concepts in the text and on the basis their co-
occurrence in one sentence. They display the
extracted concepts in concept maps connecting those
concepts “relation strength” between which does not
exceed 0.4. Like the authors of (Clariana et al.,
2004), the authors of this work do not label the
related elements (do not sign them). These authors
used some papers in scientific journals and
conference proceedings, dedicated to the field of e-
learning, as data sources for the construction of
concept maps. According to them, constructed
concept maps can be useful for researchers who are
beginners to the field of e-learning, for teachers to
develop adaptive learning materials, and for students
to understand the whole picture of e-learning
domain.
Generally speaking, labeling of related elements
extracted from the texts being analyzed is a very
complex problem that requires execution semantic
analysis of texts. That is why many researchers note
the limitedness of statistical approaches and try to
combine statistical and linguistic tools and use the
knowledge base suitable for semantic analysis. In
particular, the authors (Oliveira et al., 2001) use
thesaurus WordNet for part-of-speech analysis of
texts. Due to determination of parts of speech in
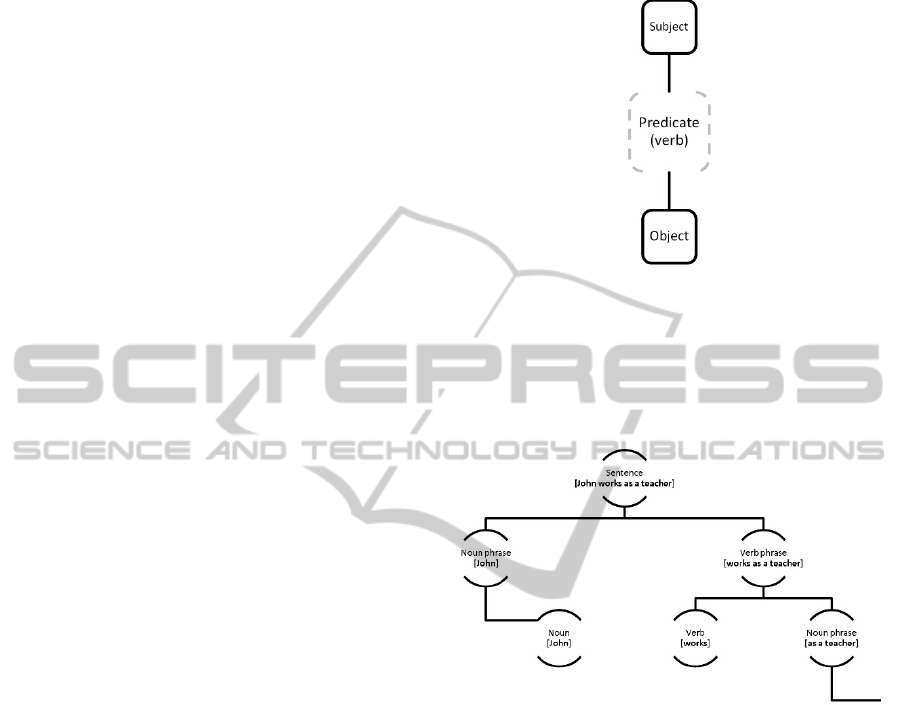
sentences they extract a predicate (the main verb)
from each sentence and form for each predicate a
triplet “subject-predicate-object”. The subject and
object are interpreted as concepts and the predicate –
as a link between the subject and object (see Figure
4). The authors of the paper were interested in
building a concept map concerning biological
kingdoms.
The authors of (Valerio et al., 2008) analyze the
structure of sentences by constructing trees of
dependences. They divide each sentence into a
group of members dependent on nouns and a group
of members dependent on the verb. They display
verbs in the links and the nouns in concepts, as
shown in Figure 5. The final goal of the authors is to
develop intelligent user interfaces to help
understanding of complex project documents and
contextualization of project tasks.
The work (Kornilakis H. et al., 2004) describes
the approach based on the use of thesaurus
WordNet, too. The authors of this work use the
lexical power of WordNet to provide the
construction of an interactive concept maps by
students.
Figure 4: The extracted triplet.
Using WordNet the authors perform processing
of different student responses revealing the meaning
of the concepts with the help synonyms, hyponyms,
meronyms, holonyms existing in the lexical base of
WordNet.
Figure 5: Dependency tree for semantic analysis.
Like the authors of (Clariana et al., 2004), the
authors of (K.Rajaraman et al., 2002) search for
structures noun-verb-noun in sentences. They use
verbs as designations of links and display nouns in
concepts. The authors of (Valerio et al, 2012) use
not only verbs but also prepositional groups of the
English language which designate possessiveness
(of), direction (to), means (by), etc. for designation
of links.
All the enumerated works demonstrate quite
good results for extraction of concepts and relations.
The problem only occurs when marking relations,
i.e. when allotting semantics to relations.
Interpretation of verbs and prepositional groups as
relations is one of the ways to solve this problem
which requires the use of linguistic tools and
dictionaries.
DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications
250
3 PROPOSED APPROACH
We have already used the approach proposed in this
work for another purpose - to build an associative
thesaurus (Nugumanova et al., 2014). In our opinion,
the difference between thesauri and concept maps is
that concept maps are more subjective, they depend
on the point of view of their creator, while thesauri
are intended to be used as a tool of standardization
and unification of the vocabulary of the domain.
3.1 Extraction of Concepts
The first step of our approach is extraction of
concepts. We consider the words which are
characterized by a strong attachment to the domain
as concepts. To find and select such words, we use
Pearson’s criterion, one of the applications of which
is the test for independence of two events (Zheng et
al., 2009). In our case, this test allows to estimate
independence of a word and the domain. The null
hypothesis of the test is that there is no dependence
(link) between a word and domain that means that
the considered word occurs with approximately
equal frequency in the texts of the domain and the
texts of other themes. Consequently, an alternative
hypothesis is that there is dependence between a
word and the domain that means that the frequency
of the word occurrence in the texts of the domain is
higher than in the texts of other themes.
All of the above means that Pearson’s criterion
for independence compares distribution of the word
in two sets of documents: a positive set (the
documents of the domain) and a negative one (the
documents of other themes). The formula that allows
to estimate such distribution for each word has the
following form:
=
( + + + )( − )
( + )( + )( + )( + )
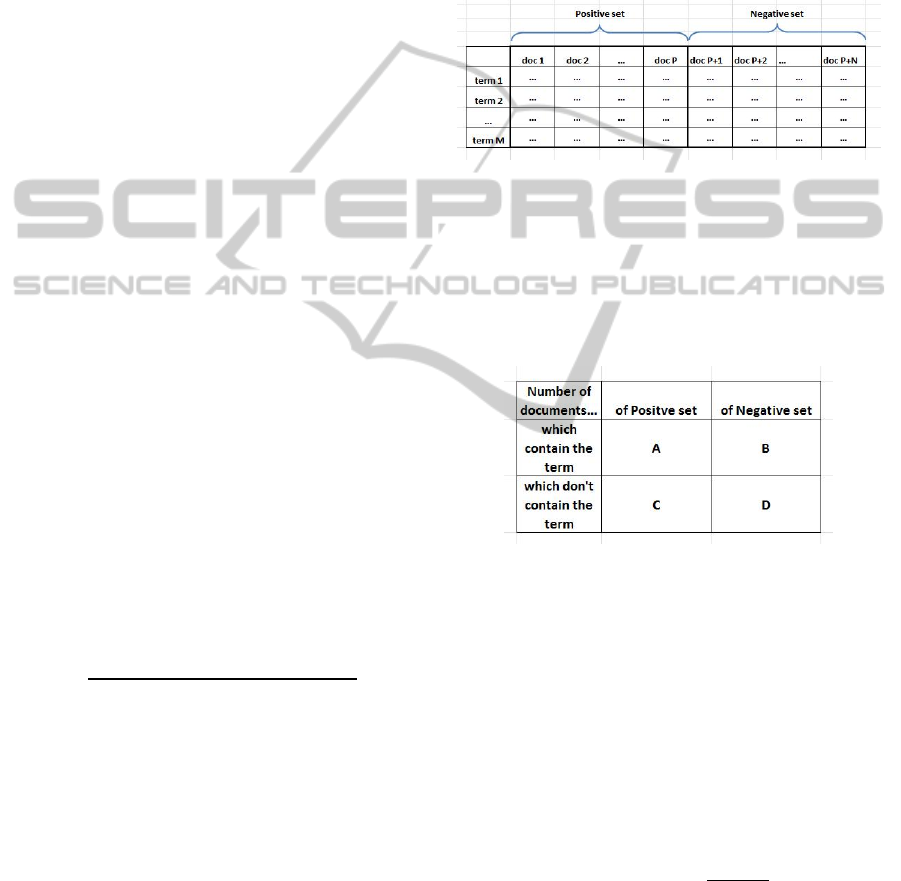
where A is the number of documents of the positive
set containing this word, B is the number of
documents of the negative set containing the word,
C is the number of documents of the positive set not
containing this word, D is the number of documents
of the negative set not containing the word.
For a technical realization of the test we should
prepare a collection of documents consisting of two
parts: a positive set of documents containing
teaching materials from a subject domain and a
negative set of documents containing various texts
from other desirable more general themes (culture,
news, events, etc.). Then we should carry out
tokenization of the obtained texts, i.e. division into
words, lemmatization (reduction of words to normal
forms) and removal of stop-words. As result of such
preprocessing we obtain a list of unique words
(terms) of the collection. After that we can construct
a term-document matrix the lines of which
correspond to terms, columns – to documents and
elements – to frequencies of using terms in
documents (see Figure 6).
Figure 6: Term-document co-occurrence matrix.
Now, for each chosen term we can calculate the
values A, B, C, D as described above (see Figure 7),
after that, using the formula we can calculate the
value of Pearson’s criterion. If the value of
Pearson’s criterion appears to be higher than a
threshold we will use this term as a concept.
Figure 7: The contingency table for the Chi-squared test.
3.2 Extraction of Relations
The obtained term-document matrix contains
information concerning links between terms and
documents. To extract relations between concepts,
we should concentrate on links between terms, i.e.
go on to a term-term matrix. For this, we should find
pairwise distances between terms which are
presented by vectors-lines in the initial term-
document matrix. The distance can be calculated
using the cosine measure:
= cos
(
̅,
)
=
̅ ∙
|
|
∙
|
|
where с is the sought for distance; x, y are any two
lines in the initial term-document matrix
corresponding to the pair of terms. The obtained
values (distances) between the terms are measured
by figures in the range from 0 to 1. The higher the
AutomaticGenerationofConceptMapsbasedonCollectionofTeachingMaterials
251

proximity between vectors-terms, the less is the
angle, the higher is the cosine of the angle (cosine
measure). Consequently, maximum proximity is
equal to 1, and minimum one is equal to 0.
The obtained term-term matrix measures the
proximity between terms on the basis of their co-
occurrence in documents (as coordinates of vectors-
terms are frequencies of their use in documents).
The latter means that the sparser the initial term-
document matrix, the worse is the quality of the
term-term proximity matrix. Therefore, it is
expedient to save the initial matrix from information
noise and rarefaction with the help of the latent
semantic analysis (Deerwester et al., 1990). The
presence of noise is conditioned by the fact that,
apart from the knowledge about the subject domain,
the initial documents contain the so-called “general
places” which, nevertheless, contribute to the
statistics of distribution.
We use the method of latent semantic analysis
for clearing up the matrix from information noise.
The essence of the method is based on
approximation of the initial sparse and noised matrix
by a matrix of lesser rank with the help of singular
decomposition. Singular decomposition of matrix A
with dimension M×N, M>N is its decomposition in
the form of product of three matrices – an
orthogonal matrix U with dimension M×M, diagonal
matrix S with dimension M×N and a transposed
orthogonal matrix V with dimension N×N:
=
.
Such decomposition has the following
remarkable property. Let matrix A be given for
which singular decomposition =
is known
and which is needed to be approximated by matrix
with the pre-determined rank k. If in matrix S
only k greatest singular values are left and the rest
are substituted by nulls, and in matrices U and V
T
only k columns and k lines are left, then
decomposition
=
will give the best approximation of the initial matrix
A by matrix of rank k. Thus, the initial matrix A with
the dimension M×N is substituted with matrices of
lesser sizes M×k and k×N and a diagonal matrix of k
elements. In case when k is much less than M and N
there takes place a significant compression of
information but part of information is lost and only
the most important (dominant) part is saved. The
loss of information takes place on account of
neglecting small singular values, i.e. this loss is the
higher, the more singular values are discarded. Thus,
the initial matrix gets rid of information noise
introduced by random elements.
3.3 Summary
The extracted concepts and relations must be plotted
on a concept map. Let us repeat that as concepts or
nodes of a graph we use all terms for which
Pearson’s criterion is higher than a certain threshold
value determined experimentally. In literature the
value of 6.6 is indicated as a threshold but by
varying this value it is possible to reduce or increase
the list of concepts. For example, a too high value of
the threshold will allow to leave only the most
important terms which have the highest values of
Pearson’s criterion.
In the same way the number of extracted
relations can be varied. If among all pairwise
distances in the term-term matrix, the values lower
than a certain threshold are nulled, the edges (links)
will connect only the concepts the proximity
between which is higher than the indicated
threshold.
4 EXPERIMENTS
To carry out experiments, we chose the subject
domain “Ontology engineering”. The documents
representing chapters from the textbook (Allemang,
D. et al, 2011) formed a positive set of the teaching
collection. Besides, some articles from other themes
formed a negative set of the teaching collection.
Tokenization and lemmatization from the collection
resulted in a thesaurus of unique terms. The use of
Pearson’s criterion with the threshold value of 6.6
allowed to select 500 key concepts of the subject
domain. Table 1 presents the first 10 concepts with
the greatest value of the criterion.
Table 1: The first 12 concepts of the subject domain.
No
Concept Chi-square test value
1 semantic 63.69
2 Web 59.95
3 property 59.87
4 manner 57.08
5 model 53.74
6 class 52.40
7 major 51.71
8 side 50.78
9 word 50.59
10 query 44.09
11 rdftype 37.41
12 relationship 35.71
DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications
252
Then the constructed term-document matrix was
approximated by a matrix of the rank 100 with the
help of singular decomposition.
On the basis of the obtained matrix, pairwise
distances between terms-lines were calculated using
cosine measure. Thus, the transfer from a term-
document matrix to a term-term matrix was carried
out. Table 2 presents, as an example, some pairs of
terms with different indexes of proximity. Only the
links the proximity values of which exceeded 0.3
were left as relations significant for construction of a
concept map.
Table 2: The samples of various extracted relations.
No
First concept Second
concept
Relation
strength
1 OWL Class 0.54
2 OWL Modeling 0.34
3 OWL member 0.37
4 Property Class 0.35
5 Result Pattern 0.37
6 Term Relationship 0,33
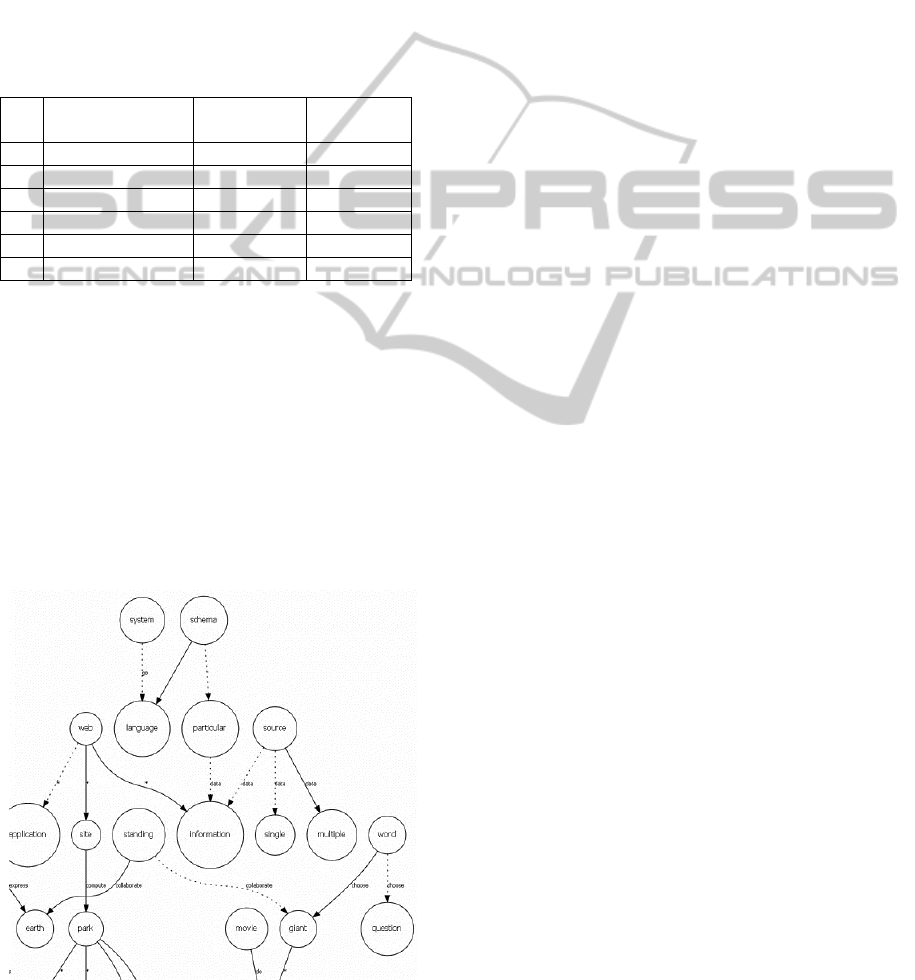
Having obtained all concepts and links, we
constructed a graph of the concept map. The
concepts were taken as nodes of the graph and
relations between concepts were taken as edges. As
the general structure of the map is too large for
analysis, we present a fragment of this map in Figure
8.
The results demonstrate one important limitation
of our approach, it is strongly influenced by the
selection of negative set. This is one of the
problematic aspects that need to be investigated in
the future works.
Figure 8: Fragment of the concept map.
5 CONCLUSIONS
The results of experiments were submitted for
analysis to two independent experts in the subject
domain. The experts noted the following advantages
of automatic generation of concept maps: quickness,
effectiveness, completeness and actuality. However,
they marked that large dimensions of concept maps
require more intellectual methods of their
processing; the further work will be related to this
theme.
This work is part of a project carried out in the
Al-Farabi Kazakh National University and East
Kazakhstan State Technical University, the goal of
which is to develop efficient algorithms and models
of semi-structured data processing, on the basis of
modern technologies in the field of the Semantic
Web using the latest high-performance computing
achievements to obtain new information and
knowledge from unstructured sources, large amounts
of scientific data and texts.
ACKNOWLEDGEMENTS
Research is funded under Kazakhstan government
scientific grant "Development of intellectual high-
performance information-analytical search system of
processing semi-structured data".
REFERENCES
Akhmed-Zaki, D., Mansurova M., Pyrkova A., 2014.
Development of courses directed on formation of
competences demanded on the market of IT
technologies. In Proceedings of the 2014 Zone 1
Conference of the American Society for Engineering
Education, pages 1–4. Scopus.
Chen, N. S., Kinshuk Wei, C. W., and Chen, H. J., 2008.
Mining e-learning domain concept map from academic
articles. Computers & Education, 50(3): 1009–1021.
Clariana, R. B., and Koul, R., 2004. A computer-based
approach for translating text into concept map-like
representations. In Proceedings of the First
International Conference on Concept Mapping,
Pamplona, Spain, pages 131–134.
Allemang, D., and Hendler, J., 2011. Semantic Web for
the Working Ontologist (Second Edition). Elsevier
Inc.
Deerwester, S. C., Dumais, S.T., Landauer, T.K., Furnas,
G.W., Harshman, R.A., 1990. Indexing By Latent
Semantic Analysis. Journal of the American Society of
Information Science, 41(6): 391–407.
AutomaticGenerationofConceptMapsbasedonCollectionofTeachingMaterials
253

Kornilakis H. et al., 2004. Using WordNet to support
interactive concept map construction. In Proceedings
of the IEEE International Conference Advanced
Learning Technologies, pages 600-604. IEEE.
Nugumanova, A., Issabayeva, D., Baiburin, Ye. Automatic
generation of association thesaurus based on domain-
specific text collection. In Proceedings of the 10th
International Academic Conference, pages 529-538.
Oliveira, A., Pereira, F.C., and Cardoso, A., 2001.
Automatic reading and learning from text. Paper
presented at the international symposium on artificial
intelligence Kolhapur, India.
Rajaraman K., and Tan, A.H., 2002. Knowledge
Discovery from Texts: A Concept Frame Graph
Approach. In Proceedings of the 11th Int. Conference
on Information and Knowledge Management, pages
669–671.
Sherman, R., 2003. Abstraction in concept map and
coupled outline knowledge representations. Journal of
Interactive Learning Research, Vol. 14.
Valerio, A., Leake, D., 2008. Associating documents to
concept maps in context. Paper presented at the third
international conference on concept mapping, Finland.
Valerio A., Leake D. B., Cañas A. J., 2012. Using
automatically generated concept maps for document
understanding: a human subjects experiment. In
Proceedings of the 15 Int. Conference on Concept
Mapping, pages 438–445.
Villalon, J., Calvo, R. 2008. Concept map mining: A
definition and a framework for its evaluation. In
Proceedings of the International Conference on Web
Intelligence and Intelligent Agent Technology, Vol. 3,
pages 357–360.
Villalon J., Calvo R., Montenegro R., 2010. Analysis of a
gold standard for Concept Map Mining – How humans
summarize text using concept maps. In Proceedings of
the Fourth International Conference on Concept
Mapping, pages 14–22.
Zheng Z., X. Wu, and R. Srihari, 2004. Feature Selection
for Text Categorization on Imbalanced Data. ACM
SIGKDD Explorations Newsletter vol. 6:80–89.
Zubrinic, K., Kalpic, D., and Milicevic, M., 2012. The
automatic creation of concept maps from documents
written using morphologically rich languages. Expert
Systems with Applications, 39(16):12709–12718.
DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications
254
