
Semantic and Structural Performer Clustering in BPMN Models
Transformed into Social Network Models
Wiem Khlif
1
and Hanêne Ben-Abdallah
1,2
1
Mir@cl Laboratory, University of Sfax, Sfax, Tunisia
2
King Abdulaziz University, Jeddah, K.S.A.
Keywords: BPM, Knowledge Discovery, Knowledge Rediscovery, Affiliation, Restructuring, Social Network Model,
Hierarchical Clustering.
Abstract: Current trends in organization restructuring focus on the social relationships among the organizational
actors in order to improve the business process. Proposed business process model restructuring approaches
adopt either social network discovery or rediscovery techniques. Social network discovery uses semantic
information to guide the affiliation process during its analyses, whereas social network rediscovery uses
structural information to identify groups in the social network. In this paper, we propose a hybrid method
that exploits both knowledge discovery and rediscovery to suggest a new structure of a business process
model that is based on performers clustering. Using the context concept, the proposed method applies a
hierarchical clustering algorithm to determine the performer partitions; the algorithm uses two newly
defined distances that account for the semantic and structural information. The method is illustrated and
evaluated experimentally to analyze its performance.
1 INTRODUCTION
Among the recent research efforts to making
Business Process Management (BPM) more
efficient, several researchers have been investigating
restructuring techniques that are centered on the
organizational perspective or people (Oinas-
Kukkonen et al., 2010). The main hypothesis of
these techniques is that social relationships among
people or organizational units affect the overall
performance of the business process model. Starting
from this hypothesis, several researchers have been
examining how to apply the concept of social
network and its analysis methods to business process
modelling. Their objective is to restructure the
organization so that its business process model
becomes more "efficient".
The so-far proposed approaches adopting social
network techniques for BPM can be divided into two
categories: social network rediscovery (Van der
Aalst et al., 2005) (Choi et al., 2007), (Song and Van
der Aalst, 2008) (Hong et al., 2012) (Boulmakoul
and Besri, 2013), and social network discovery
(Battsetseg et al., 2013) (Kim, 2013). Social network
rediscovery-based approaches extract structural
information from the business process event logs to
identify the connections among the performers or
organizational units, e.g., work transfers (Hong et
al., 2012).
In contrast, social network discovery-based
approaches explore the semantic perspective of a
business process model (e.g., the performers' roles)
to identify the social relationships among
organizational performers and units. Certainly, both
the structural and semantic information within an
organization are correlated and influence one
another. Hence, using exclusively either a
rediscovery approach or a discovery approach
reduces the scope of possible analyses that can be
made. Consequently, this may reduce the domain of
possible restructuring solutions.
Our objective in this paper is to use both the
knowledge discovery and rediscovery approaches to
find an affiliation of well-connected performers (the
structural aspect) that have similar profiles (the
semantic aspect). To do so, we introduce a new
definition of affiliation that includes both aspects,
and a new community detection method based on
the new definition. The community detection
method uses two new distances we define to account
for the structural and semantic aspects. It is based on
a hierarchical clustering algorithm that partitions the
performers (actors and/or organizational units) into
79
Khlif W. and Ben-abdallah H..
Semantic and Structural Performer Clustering in BPMN Models Transformed into Social Network Models.
DOI: 10.5220/0005555800790086
In Proceedings of the 10th International Conference on Software Engineering and Applications (ICSOFT-EA-2015), pages 79-86
ISBN: 978-989-758-114-4
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

sets of well-connected performers with similar
profiles. The connection reflects the structural/work
flow dependencies among the performers within the
organization, whereas the profile similarities reflect
the semantic relationships among them--e.g., in
terms of their affiliation to a pool and to a lane, their
assigned roles, and their permissions to perform the
activities.
Once the performer communities are identified,
we can apply the set of graph optimization rules we
proposed in (Khlif and Ben-Abdallah, 2015). These
rules combine the semantic and structural aspects to
reduce the control flow complexity of a business
process modelled in the Business Process Modelling
Notation (ISO/IEC 19510, 2013).
The remainder of this paper is structured as
follows: Section 2 overviews existing approaches for
organization restructuring. Section 3 presents the
definition of the context concept. Section 4 shows
how the new context concept can be used in a
method for identifying performer affiliations. In
section 5, we summarize the presented work and
outline its extensions.
2 RELATED WORK
2.1 Rediscovery-based Approach
Adopting a rediscovery approach, (Boulmakoul and
Besri, 2013) combine structural analysis with Q-
analysis and Social Network Analysis (SNA)
techniques. SNA plays an important role since it
evaluates the relationships among performers, roles,
units and even an entire organization (Stanley and
Katherine, 1999). This kind of analysis can extract
important information to improve the flow of
communication in an organization and it allows
managers to discover the way the work is being done
in the informal way (Noel et al., 1979).
To re-engineer an enterprise organization,
(Boulmakoul and Besri, 2013) define a set of
operations applicable along two viewpoints:
Organizational and performer status. They show
how several framework and toolkit can be used for
process mining of the organizational perspective,
visualizing and analyzing the organizational
structure.
In (Hong et al., 2012), the authors present a
methodology to derive an organizational structure.
The methodology has four phases. The first one
collects source data from BPMN models measured
by transfer-of-work metrics; the metrics were
defined to derive relations between resources from
process logs (Van der Aalst et al., 2005) (Choi et al.,
2007), (Song and Van der Aalst, 2008).
In the second phase, the BPMN model is
transformed into a process network that is
diagnosed, in the third phase, by five problems-
oriented approaches: verticality of workflows,
degree of bottlenecks, core competence of business
processes, authority that corresponds to the position,
and degree of business cooperation.
The aforementioned works are based only on
knowledge rediscovery relying on the structural
aspect. They can identify central nodes in the
network and they can take measures over the
structure of the social network model such as node
centrality, node betwenness, density, geodesics
distance, diameter, connectivity of the graph, etc.
2.2 Discovery-based Approach
Besides the rediscovery approaches, other
approaches focused on discovering social network
knowledge through exploring the human perspective
of a group of models (Ahn et al., 2014).
More specifically, the authors in (Battsetseg et
al., 2013) (Kim, 2013) propose an approach for the
workflow-supported affiliation networking
knowledge discovery. They propose various
formalisms (Kim et al., 2014) and algorithms to
model, discover, and visualize the workflow
performer-role affiliation networking knowledge
from an Information Control Net (ICN) based
workflow model.
In the discovery-based approaches, the profile
information is typically represented as a matrix used
by algorithms to discover and analyse performer-
role affiliation networking and activity-performer
affiliation. In the affiliation network, performers are
linked through their joint participation in performing
roles. Conversely, roles are assigned to the
performers who are involved in the roles. Through
the performer-role affiliation networking knowledge,
it is possible to visualize in a workflow model how
performers and roles are simultaneous.
2.3 Discussion
Existing approaches deal with each type of
knowledge separately. However, using either social
network knowledge rediscovery or social network
knowledge discovery reduces the scope of the
information that can be extracted: An affiliation
presents a well-connected performer but not
necessarily similar in terms of theirs profiles. In
addition, an affiliation may be composed of similar
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
80
but loosely connected performers. In other words,
such separate use of the knowledge may lead to
inefficient restructuring solutions, which would
impact the organization performance.
3 STRUCTURE AND SEMANTICS
BASED CONTEXT
BPMN provides for the modelling of tasks assigned
to actors/performers. Hence, a BPMN business
process model
P
can be seen as a social network
model
()()
P
CEVG ,,
where:
−
()
EVG ,
is an undirected graph representing the
structure of the business process, with
V
being
the set of
n
nodes representing the performers
(i.e., the actors in the BPMN model), and
E
being the set of
m
edges connecting the nodes
(i.e., the flows in the BPMN model); and
−
P
C
is the semantic information of the network
model.
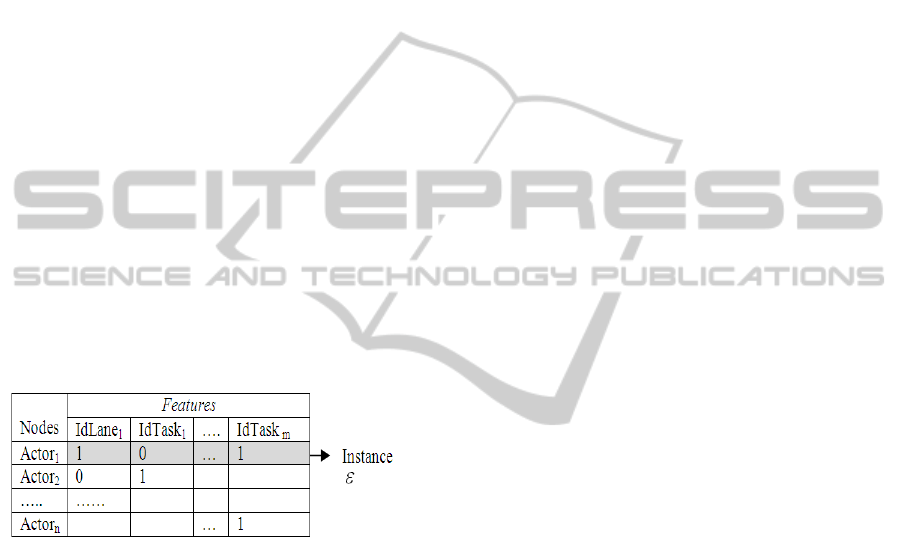
Table 1: Tabular representation of the semantic
information
P
C
in a social network model.
The semantic information
P
C
represents the
individual information of each performer in the
business process model: which tasks are performed
by the actor, and each actor's lane membership. It is
defined as a matrix of nodes x features. Each node
(i.e. performer) in the business process is described
by one row of features we call instance. The features
included in
P
C
may cover the functional,
informational, organizational and behavioural
contexts, or a combination of them. Table 1 shows a
tabular representation of an example of
P
C
.
The context concept is used to divide the set of
features into subsets according to different
perspectives
(Curtis et al., 1992). The features
provide for the discovery of unseen information
belonging to each perspective (functional,
informational, behavioural and organizational) and
related to each performer.
The functional perspective (Curtis et al., 1992)
represents what process elements are being
performed. The BPMN main concept that reflects
this perspective is Activity. In this perspective, the
feature that can be derived is IdTask, IdSubProcess.
In addition, since the informational perspective is
represented in terms of data (Curtis et al., 1992), the
data input and data output can be used as a set of
features. Furthermore, the organizational perspective
represents where and by whom process elements are
performed (Curtis et al., 1992). The main BPMN
concepts that reflect the organizational perspective is
Lane and Pool. The information that can be derived
from these BPMN concepts is IdLane and IdPool.
With the aforementioned concepts, we can now
define, for each node, the context which is a
particular set of values for each feature.
Definition 1: (Context
P
C
). Given a set of features
F
, a context
P
C
is one of the m-combinations of
the
m
elements of
F
. Note that
m
P
FC ∈
.
Definition 2: (Augmented social network model
+
P
): Given a social network model
()()
P
CEVG ,,
where
G
is the graph representing the structural
aspect,
P
C
the semantic aspect as a context, the
augmented social network model is defined as
()
ACGP
P
,,
+
where
A
is the affiliation variable that
is derived from
G
and
P
C
.
The affiliation variable
A
of an augmented
social network
+
P
can be derived either from the
structural aspect, contained in
G
, or from the
semantic variables contained in
.
P
C
In the first
case, we assume that
φ
=
P
C
; this means that the
determination of the affiliation
A
becomes a
general problem of graph clustering. Note that graph
clustering approaches use only the structure to find
cohesive groups. For
()
φ
,VG
, only
P
C
is available,
the affiliation variable
A
can be generated using
traditional data clustering methods that use
(typically) vector representations of the data. Using
this data these methods produce groups of close
elements according some distance measure.
There is a gap between the available clustering
approaches designed for each one of these cases.
This gap opens a new study field, looking for new
ways to generate affiliation variables that integrate
the structural and the semantic aspect.
SemanticandStructuralPerformerClusteringinBPMNModelsTransformedintoSocialNetworkModels
81

4 CLUSTERING STRUCTURAL
AND SEMANTIC ASPECTS
The main objective of our work is to use both
structural and semantic aspects of a business process
model to restructure it based on the social network.
To do so, we need to generate the performer
partitions which are the result of a clustering
process. The obtained performer affiliation should
represent groups of well-connected and similar
performers.
Figure 1 presents the general diagram of our adopted
structural and semantics clustering.
Figure 1: Performer affiliation using the structural and
semantic aspects.
First, the context
P
C
from the social network
model is used to find an auxiliary affiliation of
performers based on the semantic aspect
SEM
A
. This
affiliation contains groups of similar performers. It
is obtained by the semantic information represented
by a proposed distance called Task-Lane
LPA
D
−−
.
This distance is used to determine the number of
tasks and lanes that are different for any pairs of
actors. In addition, to account for
the structural
aspect, the semantic distance
LPA
D
−−
is multiplied
by the structural distance
F
D
which expresses the
proportion of the sequence flow connecting the
performers. The integration of structural and the
semantic aspects produces a new performer’s
affiliation
STRSEM
A
−
that contains information from
both aspects.
Finally, in order to cluster the performers, we
adapt the hierarchical algorithm (Kantardzic, 2002)
to our domain to generate the partition groups of the
performers according to the similarities of their
features and the relationships between them. The
steps of our agglomerative hierarchical clustering
are presented in Algorithm 1. This algorithm has two
main advantages: it requires no a priori information
about the number of clusters required, and it is easy
to implement.
Algorithm 1
Let
{}
n
xxxxX ,....,,
321
=
be the set of data points.
1. Begin with the disjoint clustering having level
()
00 =L
and sequence number
0=m
.
2. Find the least distance pair of clusters in the
current clustering, say pair (r), (s), according
to:
()()
[]
()( )
[]
jidsrd ,min, =
where the minimum is over all pairs of clusters in
the current clustering.
3. Increment the sequence number:
1+= mm
.
Merge clusters (r) and (s) into a single cluster
to form the next clustering m. Set the level of
this clustering to
() ()()
[]
srdmL ,=
.
4. Update the distance matrix, D, by deleting the
rows and columns corresponding to clusters
(r)and (s) and adding a row and column
corresponding to the newly formed cluster.
The distance between the new cluster, denoted
(r,s) and old cluster(k) is defined in this way:
()( )
[]
()()
[]
()()
[]
skdrkdavergemeansrkd ,,,,, =
5. If all the data points are in one cluster then
stop, else repeat from step 2.
4.1 Example
To illustrate our approach, we will use the “supply
management business process” shown in Figure 2.
The task assignment to actors and lanes are listed
in Table 2. Table 3 shows the corresponding binary
affiliation matrix “Activity-Performer-Lane”.
Each row in Table 3 expresses a vector of
features representing one actor. In our example, we
aim to cluster the actors which belong to the same
pool: “supply management process’’. We used the
following features: IdTask to represent which tasks
are performed by the actor, and Id-Lane to express
each actor's lane membership.
An “Activity-Performer-Lane” (A-P-L)
affiliation network model is graphically represented
by a bipartite graph, and it is mathematically
represented by an affiliation matrix (see Table 3).
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
82

Figure 2: BPMN example: Supply management business process.
Table 2: Tasks assignment to actors and lanes.
Each entry x
i,j
of the A-P-L matrix is filled
according to the following rule:
=
otherwise
LlaneorTactivitiywithaffiliatedisAperformerif
x
jji
ji
0
,,,1
,
Based on Table 3, we calculate the first distance D
A-
P-L
as the Euclidean distance between two actors
(two vectors in Table 3). D
A-P-L
determines the
number of tasks and lanes which are different
between a pair of actors. Table 4 shows the values
of the activity-performer-lane distance.
The second calculated distance is the flow
distance D
F
:
1
1
1
1
+
−
+
=
FTF
F
NN
D
(1)
where: N
F
is the total number of sequence flows sent
directly from one actor to another, and N
FT
is the
total number of sequence flows in the model. This
distance represents the distance between actors in
terms of how work is moved among them. The 1
added in the denominators is to avoid a division by
0. Table 5 lists the D
F
values for the running
example. Based on D
A-P-L
and D
F
, we calculate the
total distance as follows:
()
TFLPAF
ddDDD ++=
−−
ε
*
(2)
We add
()
,
TF
dd +
ε
,
in formula (2), in order to avoid
the case of a null distance when D
F
=0 and
D
A-P-L
≠0
and conversely. We suppose that
ε
=0.
SemanticandStructuralPerformerClusteringinBPMNModelsTransformedintoSocialNetworkModels
83

Table 3: Binary affiliation matrix “Activity-Performer-Lane” of Figure 2.
Table 4: Euclidian distance D
A-P-L
between actors.
Table 5: The D
F
distance between actors.
Table 6: Total distance D between actors.
Table 6 summarizes the total distance
D
for the
running example. This distance matrix is the input to
the
hierarchical clustering algorithm to determine
the actor affiliation.
To illustrate the application of this task, we next
show how the classification objective, making
homogeneous and distinct groups, can be
mathematically formalized by using the concepts of
intra-class inertia (Kantardzic, 2002). The goal is to
find the partition K classes whose inertia intra class
is minimal.
The inertia is defined as follows:
Let
G
is a group of individuals partitioned into nbg
classes
.....,
21 nbg
ggg
The intra-class inertia I is equal to:
()
()
!2!2
2
where
2
,
1
!
1
,
21
2
21
×−
=
=
=
∈
i
g
g
nbg
i
g
gcc
g
ccd
nbg
I
i
i
i
i
(3)
4.2 Application of Hierarchical
Algorithm Clustering
Hierarchical clustering is a method of cluster
analysis that seeks to build a hierarchy of clusters.
We used the agglomerative strategy for hierarchical
clustering which a "bottom up" approach: each
observation starts in its own cluster, and pairs of
clusters are merged as one moves up the hierarchy.
The linkage criterion determines the distance
between sets of observations as a function of the
pairwise distances between observations. In our
example, we use the average linkage clustering. The
following steps are conducted over the running
example:
STEP1: Each observation is in its own cluster: {A1}
{A2}, {A3}, {A4}, {A5}, {A6}, {A7}. The input
distance matrix
(L = 0 for all the clusters) is the total
distance shown in Table 6.
In the first step, the inertia is equal to zero:
0
1
=I
STEP2: Based on the input distance matrix, the
nearest pair of actors are (A5, A7), (A5, A6), and (A6,
A7). We select for example, A5 and A7, at distance
0.127. These actors are merged into a single cluster
called
"A5/A7". The level of the new cluster is L
(A5, A7) = 0.127 and the new sequence number is m
= 1.
Then we compute the distance from this new
compound object to all other objects. In average link
clustering the rule is that the distance from the
compound object to another object is equal to the
mean average distance from any member of the
cluster to the outside object. So the distance from
"A5/A7"
to A6 is chosen to be 0.127, which is the
average distance from A5 to A6, and A6 to A7.
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
84

After merging A5 with A7
,
we obtain the
following matrix representing the clusters:
{A1} {A2}, {A3}, {A4}, {A5, A7}, {A6}
Table 7: Distance matrix for step 2.
We calculate then the inertia that corresponds to
this step: I
2
=0.0026.
STEP3: In this step, because
min d(i,j)=d((A5/A7),A6) = 0.127, then we merge
"A5/A7"
and A6 into a new cluster called {A5,
A6,A7}, which gives us L((A5/A),A6)=0.127, m=2
distance matrix shown in Table 8.
Table 8: Distance matrix for Step 3.
The derived clusters are: {A1}, {A2}, {A3},
{A4}, {A5, A7, A6} and the inertia is I
3
=0.0032.
STEP4: Because we have
min d(i,j)=d(A1,A2) = 0.16, then we merge A1/A2
into a new cluster called {A1,A2}. At the end of this
step, we have L(A1,A2) = 0.16, m=3 and the
distance matrix shown in Table 9.
At the end of this step, the obtained clusters are:
{A1, A2}, {A3}, {A4}, {A5, A7, A6} and the inertia
is I
4
=0.009.
Table 9: Distance matrix for step 4.
STEP5: Because we have min d(i,j)=d((A1/A2),
A3)=0,251, then we merge
A1/A2 with A3 into a
new cluster called {A1,A2,A3}. Thus, we have:
L(A1/A2)=0.251, m=4
and we obtain the distance
matrix of Table 10.
Table 10: Distance matrix for step 5.
At this step, the obtained clusters are:{A1, A2, A3},
{A4}, {A5, A7, A6} and the inertia is: I
5
=0.019.
STEP6: min d(i,j)=d((A1/A2/A3),A4) = 0.257
which
leads to merging A1/A2/A3 with A4
into a new
cluster called {A1, A2, A3, A4}.
L((A1/A2/A3),A4) = 0.257, m=5
After merging A1/A2/A3 with A4 we obtain the
distance matrix of Table 11, the custers: {A1, A3,
A2, A4}, {A5, A7, A6} with an inertia I
6
=0.034.
Table 11: Input distance matrix for step 6.
STEP7: Finally, we merge the last two clusters at a
level of 5.2. As depicted in figure 3, the inertia
reaches its highest value in this step. We can see that
the difference between the inertia values in two
consecutively steps increases from step 5 to step 6.
The obtained result shows that the difference
between the inertia in a time (t) and (t-1) must not
exceed
015.0=
ε
() ( )
.
1
ε
≤−
−tt
II
Figure 3: The inertia curve during the six iterations.
In this example, the clustering at step 5 is
considered optimal: {A1, A2, A3}, {A4}, {A5, A7,
A6}. Based on this clustering, we obtain three lanes:
the first lane contains the actors {A1, A2, A3}. The
second lane contains the actor {A4} and the last lane
contains the actors {A5, A7, A6}.
SemanticandStructuralPerformerClusteringinBPMNModelsTransformedintoSocialNetworkModels
85

4.3 Experimental Evaluation
To evaluate the obtained inertia threshold, we
worked on forty business processes models. In this
empirical study, we applied the hierarchical
algorithm to forty business process models, and we
calculated the inertia for each case. The results
showed that the best clustering is obtained in 36
models with a threshold inertia value that does not
exceed 0.015.
5 CONCLUSIONS
The information contained in a socio-semantic
network is tied both to certain features pertinent to
individual performers (semantic information) and
their organizational relationships (structural
information). Such information allows to perform
more comprehensive analyses over the network from
different perspectives, which provides for better
restructuring decisions.
Unlike existing the approaches which use one
type of information, in this paper, we proposed an
approach for social network restructuring that uses
both structural and semantic information. Our
approach relies on the definition of the concept of
context which augments the social network with
semantics pertinent to the business process. In
addition, it uses two new distances that account for
the semantic and structural information, and applies
a hierarchical clustering algorithm to identify
performer clusters. Each cluster represents an
affiliation of well-connected performers that have
similar profiles.
We are currently defining a graph-based method
that uses the obtained clusters to restructure an
organization. This method extends our preliminary
identified set of rules for transforming a BPMN
model into a behaviourally equivalent one (Khlif and
Ben-Abdallah, 2015).
REFERENCES
Ahn, H., Park, Ch., Kim, K.P., 2014. A correspondence
analysis framwork for workflow-supported performer-
activity affiliation networks. In ICACT'14, 16th Intern.
Conf. on Advanced Communication Technology. pp.
350-354. IEEE.
Battsetseg, A., Hyun, A., Lee, Y., Park, M., Kim, H.,
Yoon, W., Kim, K. P., 2013. Organizational Closeness
Centrality Analysis on Workflow supported Activity-
Performer Affiliation Networks. In ICACT’13, 15th
International Conference on Advanced
Communication Technology. pp. 154-157.
Boulmakoul, A., Besri, Z., 2013. Scoping Enterprise
Organizational Structure through Topology
Foundation and Social Network Analysis. In
INTIS’13, Innovation and News Trends in Information
Systems. Tanger, Morocco.
Choi, I., Song, M., Kim, K.P., and Lee, Y., 2007. Analysis
of social relations among organizational units derived
from process models and redesign of organization
structure. In Journal of the Korean Institute of
Industrial Engineers. 33(1) pp.11-25.
Curtis, B., Kellner, M., Over. J., 1992. Process Modeling.
Communication of the ACM. 35(9).
Hong, S., Lee, Y., Kim, J., Choi, I., 2012. A Methodology
for Redesigning an Organizational structure based on
Business Process Models using SNA Techniques. In
Journal of Innovative Computing, Information and
Control. 8(B), ISSN 1349-4198. pp. 5411-5424.
ISO/IEC 19510, 2013. Information technology -- Object
Management Group Business Process Model and
Notation. Available from: http://www.iso.org/iso/
catalogue_detail.htm%3Fcsnumber%3D62652.
Kantardzic, M., 2002. Data Mining: Concepts, Models,
Methods, and Algorithms. Wiley-IEEE Press.
Khlif, W., Ben-Abdallah, H., 2015. Integrating semantics
and structural information for BPMN model
refactoring. In SERA'15, 13
th
Intern. Conf. on Software
Engineering Research, Management and Applications.
Toulouse.
Kim, H., Ahn, H., Kim, K.P., 2014. Modeling,
Discovering, and Visualizing Workflow Performer-
Role Affiliation Networking Knowledge. In TIIS’14,
Journal of Transactions on Internet and Information
Systems. 8(2). pp. 689-706.
Kim, K.P., 2013. Discovering Activity-Performer
Affiliation Knowledge on ICN-based Workflow
Models. In Journal of information science and
engineering. 29. pp. 79-97.
Noel, M. T., Micheal, L. T., Charles, F., 1979. Social
Network Analysis for Organizations. In The Academy
of Management Review. 4(4), pp. 507-519.
Oinas-Kukkonen, H., Lyytinen, K., Yoo, Y., 2010. Social
Networks and Information Systems: Ongoing and
Future Research Streams. In Journal of the
Association of Information Systems. 11(2). pp. 61-68.
Stanley, W., Katherine, F., 1999. Social Network
Analysis: Methods and Applications. In Revue
française de sociologie. 36-4. pp. 781-783.
Song, M., Van der Aalst, W. M. P., 2008. Towards
comprehensive support for organizational mining. In
Decision Support Systems. 46(1), pp.300-317.
Van der Aalst, W. M. P., Reijers, H. A., Song, M., 2005.
Discovering social networks from event logs. In
Computer Supported Cooperative Work. 14(6), pp.
549-593.
ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications
86
