
Linear Software Models: Equivalence of Modularity Matrix to Its
Modularity Lattice
Iaakov Exman
1
and Daniel Speicher
2
1
Software Engineering Dept., The Jerusalem College of Engineering – JCE-Azrieli, Jerusalem, Israel
2
Bonn-Aachen International Center for Information Technology, University of Bonn, Bonn, Germany
Keywords: Linear Software Models, Modularity Matrix, Modularity Lattice, Formal Concept Analysis, Equivalence.
Abstract: Modularity is an important feature to solve the composition problem of software systems from subsystems.
Recently it has been shown that Software systems’ Modularity Matrices linking structors to functionals can
be put in almost block-diagonal form, where blocks reveal higher-level software modules. An alternative
formalization has been independently proposed using Conceptual Lattices linking attributes to objects. But,
are these independent formalizations related? This paper shows the equivalence of Modularity Matrices to
their respective Modularity Lattices. Both formalizations support the simplest form of software
composition, i.e. linear composition, expressed as an addition of independent components. This equivalence
has both theoretical and practical advantages. These are illustrated by comparison of both representations
for a series of case studies.
1 INTRODUCTION
Composition of software systems from subsystems
and basic components is an important problem. It is
widely accepted that modularity is essential to solve
this problem. Two independent approaches have
formalized modularity for the software composition
problem, relying on algebraic structures.
One approach uses Modularity Matrices linking
structures to their functionality. Another approach
represents relations between objects and attributes as
Lattices of formal concepts. This work shows the
equivalence of the matrix and lattice approaches,
assuring that results in either approach are valid in
the other approach as well. In other words, they are
alternative representations of the software system.
1.1 Modularity Matrix Concepts
A Modularity Matrix displays relations between two
kinds of architectural entities in a software system:
structors, the columns, and functionals, the rows.
Structors generalize UML classes (i.e. a class,
interface, aspect, sets of related classes, such as
design patterns). Functionals generalize class
functions (i.e. a method, families of functions, such
as trigonometric functions). Each 1-valued matrix
element links a structor to a provided functional.
Functionals are potential functions, not necessarily
invoked in the system. In (Exman, 2012) it was
shown by linear algebra arguments that:
• A Modularity Matrix is square – if its structors
are linearly independent and also its functionals
are linearly independent;
• A Modularity Matrix is block-diagonal – if
certain structor sub-sets provide sub-sets of
functionals, disjoint to other sub-sets; each block
is an independent module.
In a standard Modularity Matrix all the matrix
elements outside modules are zero-valued. A block-
diagonal matrix is got by reordering rows/columns.
Modularity Matrix elements are numbers used in
actual calculations. For instance, to compare the
relative modularity of different software designs of a
system one calculates the Matrix M diagonality, with
elements M
jk
(row j, column k) and dimension N:
() () ()
D
iagonality M Trace M offdiag M=−
(1)
where
1
1
() *| |
N
N
jk
j
k
offdiag M M j k
=
=
=−
(2)
1.2 Modularity Lattice Concepts
A conceptual lattice displays relations between two
109
Exman I. and Speicher D..
Linear Software Models: Equivalence of Modularity Matrix to Its Modularity Lattice.
DOI: 10.5220/0005557701090116
In Proceedings of the 10th International Conference on Software Paradigm Trends (ICSOFT-PT-2015), pages 109-116
ISBN: 978-989-758-115-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

kinds of entities: attributes and objects. Attributes
express the concepts’ intent, and object sets express
the concepts’ extent. The Top lattice node has empty
set intent and an extent as the set of all objects.
Mutatis mutandis the Bottom lattice node has empty
set extent and an intent as the set of all attributes.
A conceptual lattice is built by first preparing its
formal context, i.e. a table displaying which objects
have certain attributes, marked by X signs. In
contrast to the Modularity Matrix, the formal context
has not been defined as a matrix with numerical
matrix elements, allowing calculations. Moreover,
there are no underlying linear algebra theorems on
the formal context, such as being square or block-
diagonal. A formal context may be a rectangular
table without any specific requirements.
In this work, we make the unique decision of
generating conceptual lattices directly from given
Modularity Matrices, with the expectation that the
resulting Modularity Lattices carry on the
characteristic properties of these matrices. This work
aims to show that this is indeed the case.
To show the equivalence of a modularity matrix
to a modularity lattice, we choose to match between
matrix ‘structors’ and the lattice intent (viz.
‘attributes’) on the one hand, and match between
matrix ‘functionals’ and lattice extent (viz. ‘objects’)
on the other hand. A link between a structor and a
functional corresponds either to an attribute in the
same node as its object, or to an attribute in a node
connected to a node by a downward set of edges in
the Lattice, not passing through Top or Bottom.
The conceptual justification for this matching is
clarified as follows. UML classes represent concepts
with definite intents. For instance, the class “car” is
a type of vehicle with the intent of travelling on
roads. Cars have wheels, their speed and travelled
distance may be calculated by suitable functions (the
extent). The class “airplane” is another type of
transportation medium with a different intent, viz. to
travel by flying. Airplanes also have wheels, their
speed is also calculated by suitable functions. Thus
different classes have clearly different intents, but
may have similar extents.
Software conceptual lattices are a broader
subject than implied by the above simple examples.
They deserve extensive discussion, which is outside
of this paper scope. Here we focus on the
equivalence of Modularity Matrices and Modularity
Lattices. For further details on formal concepts, see
(Ganter, 1999), (Ganter, 2005), (Belohlavek, 2008).
The remaining
of this paper is organized as
follows. Section 2 refers to related work. Section 3
displays an introductory example. Section 4
formulates theoretical considerations. Section 5
deals with heuristics for modules’ decoupling.
Section 6 presents canonical case studies. Section 7
shows a larger system case study. The paper is
concluded by a discussion in section
8.
2 RELATED WORK
In this work we refer to the modularity matrix – e.g.
(Exman, 2014). Other matrices have also been used
in the context of modularity. For instance, the
Design Structure Matrix (DSM) proposed in
(Steward, 1981), and incorporated in ‘Design Rules’
(Baldwin, 2000). It has been applied in various
contexts – see e.g. (Cai, 2006).
Two essential differences between DSM and the
modularity matrix are: a- Linearity as an essential
idea of the modularity matrix; b- Both DSM
dimensions are labelled by the same structures.
The modularity matrix, in contrast to the DSM,
displays pairs of different entities, viz. structors to
functional links. The use of pairs of entities was
important to suggest the correspondence to
conceptual lattices, as the latter also refer to pairs of
entitities, viz. attributes and objects.
Conceptual lattices, generally known as part of
Formal Concept Analysis (FCA) were introduced in
(Wille, 1982). There are many available generic
overviews describing mathematical foundations
(Ganter, 1999), applications (Ganter, 2005) and
surveys of the field (Belohlavek, 2008).
FCA has been used as a technique for
modularization and system design. This includes
works such as (Lindig, 1997), (Siff, 1999) and
(Snelting, 2000). A specific usage of conceptual
lattices for software engineering is found in
(Heckmann, 2012).
3 INTRODUCTORY EXAMPLE:
COMMAND DESIGN PATTERN
The Command software design pattern, in the GoF
book (Gamma, 1995), serves as an introductory
example. The pattern decouples an object invoking
an action, say clicking a “Print” button, from another
object that actually prints a file. The pattern enables
generic features, such as Undo and Redo,
independently of the specific commands’ nature.
3.1 Command Modularity Matrix
The six structors in the Command Modularity Matrix
ICSOFT-PT2015-10thInternationalConferenceonSoftwareParadigmTrends
110
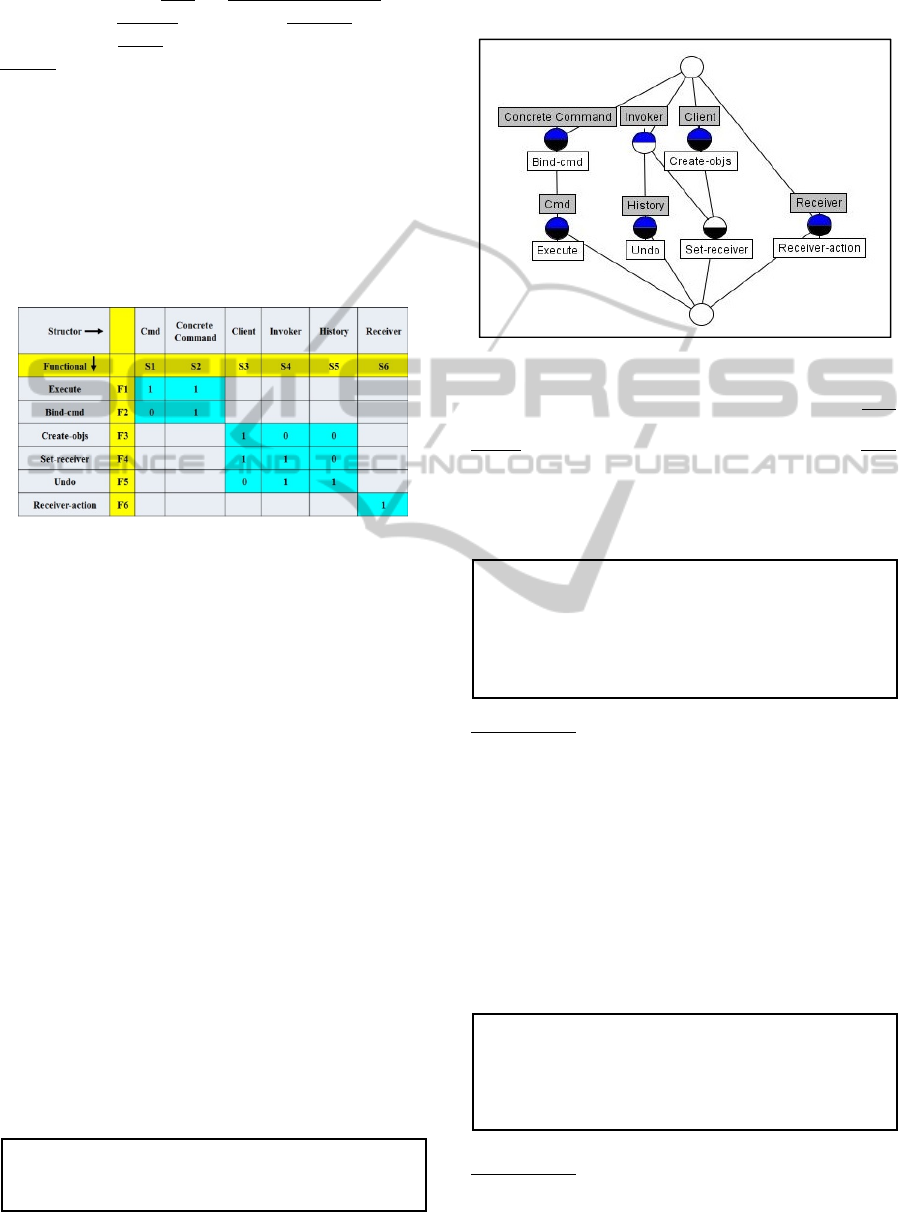
are in the list of Participants in the GoF book: an
abstract command (cmd), a concrete command (say,
Print File), an invoker (a button), a receiver (a file to
be printed), a client (initializes the application) and
history (enables undo). The Pattern functionals are:
execute, undo, create objects, bind command-to-
button, set-receiver, and the receiver action.
Block-diagonal modules, in Fig. 1, reflect the
pattern purpose: the command is decoupled from the
generic infrastructure. The top-left module is the
command itself, its abstract interface and concrete
implementation. The middle module is the generic
infrastructure: a client, the invoker and a history
mechanism for undo operations. The bottom-right
module is a specific receiver and its action.
Figure 1: Command Design Pattern Modularity Matrix.
It has six structors and functionals, forming three modules
(blue background): a- upper-left, the command; b- middle,
the generic infrastructure c- lower-right, the specific
receiver. Zeros outside modules are omitted for simplicity.
3.2 Command Modularity Lattice
We use the Modularity Matrix in Fig. 1 to generate
the Command Modularity Lattice. The result in Fig.
2, is obtained by the (Concept Explorer, 2006) tool.
4 THEORETICAL
CONSIDERATIONS
The set of Definitions and Theorems herein, for both
Modularity Matrix and Modularity Lattice, form
altogether the equivalence proof of these
representations regarding modularity.
4.1 Modularity Lattice Defined
We define a Modularity Lattice with respect to the
Modularity Matrix (Exman, Nov 2012):
Definition 1: Modularity Lattice
A Modularity Lattice is a conceptual lattice
generated from a Modularity Matrix.
A standard Modularity Lattice is generated from a
standard Modularity Matrix. From this definition
follow its characteristic properties.
Figure 2: Command Design Pattern Modularity Lattice -
Any path (or set of paths) from Top to Bottom not linked
to other paths is a module. One sees 3 modules: a- l.h.s.
with 2 attributes (Concrete Command and Cmd); b-
middle with 3 attributes (Client, Invoker, History) c- r.h.s.
with 1 attribute (Receiver). These match the matrix in Fig.
1. Nodes may have three colors: upper-half blue – an
attribute is associated with the node; lower-half black – an
object is associated with the node; white – no association.
Lemma 1: Standard Modularity Lattice
Properties
a- Its number of attributes is the same as its
number of objects;
b- No specific object is the Top; no specific
attribute is the Bottom.
Proof outline:
a- This property is obvious from the fact that the
Modularity Matrix is square;
b- This follows from the requirement that the
standard Modularity Matrix should not have
column vectors or row vectors fully consisting
of 1-valued matrix elements.
4.2 Modularity Lattice Modules
The Modularity Matrix modules are its diagonal
blocks. Modularity Lattice modules are given by:
Theorem 1: Modularity Lattice Modules
The modules of a software system in its
Modularity Lattice are the connected components
obtained when one cuts the Top and the Bottom
from the Modularity Lattice.
Proof outline:
Modules of a Modularity Matrix are diagonal
LinearSoftwareModels:EquivalenceofModularityMatrixtoItsModularityLattice
111

blocks whose set of structors and functionals are
disjoint from the respective sets of other modules.
Since structors correspond to Lattice attributes and
their functionals to the respective Lattice objects, a
set of attributes/objects disjoint to other sets has no
edges to other attributes/objects, except the Lattice
Top and Bottom. Cutting the latter from the Lattice
leaves a set of connected components corresponding
to the Modularity Matrix modules.
The converse of Theorem 1 is easily verified.
Next, we deal with different kinds of modules in
the Modularity Lattice. The paths in the next
corollary refer to connected components after
cutting edges to Top/Bottom of the Lattice.
Corollary: Modularity Lattice Module Types
1a- single path with single node – a path with no
edges to other paths, and a single node, fits a
purely diagonal Modularity Matrix module;
1b- single path with N nodes – a path without
edges to other paths, with N nodes, fits a block-
diagonal N-dimension module forming a full
lower triangular matrix in the block, in a
Modularity Matrix having no outliers.
1c- a set of connected paths – a set of paths with
edges among paths within the set, and N attributes
fits an N-dimension diagonal block, in a
Modularity Matrix having no outliers.
Proof outline:
1a- a single node means just one attribute with one
object;
1b- N nodes mean that there are N attributes, one
for each node, therefore also N objects, as the
module must be square; the full triangular
matrix within the block is needed to avoid
linear dependence among the structors in the
Modularity Matrix, since each attribute has all
the objects in its own node and below its node;
1c- N nodes mean that there are N attributes, one
for each node, therefore also N objects, as the
module must be square; since there are two or
more paths, not all attributes have all the
objects below its node in the same path.
It is straightforward to obtain module attributes
and objects in the Modularity Lattice, corresponding
to their Modularity Matrix. Going downwards (from
Top to Bottom) in any path, one uses set intersection
for objects, to obtain the respective objects of the
next node, down to one-level above the Bottom.
Going upwards in any path, one uses set intersection
for attributes, to obtain the respective attributes of
the next node, up to one-level below the Top. For
more details see e.g. (Belohlavek, 2008).
4.3 Modularity Matrix Outliers
Criterion
Formally within Linear Software Models, cohesion
is defined in terms of sparsity of the Modularity
Matrix (Exman, 2012). Sparsity of a matrix is the
ratio between the number of zero-valued elements to
the total number of elements in the matrix:
Sparsity = NumZeros/TotalNumElements (3)
In general, one expects the sparsity of modules
to be lower than the sparsity of the Modularity
Matrix elements outside the modules. Thus, the
lower is the sparsity, the higher the cohesion. This
implies a threshold of maximal sparsity inside a
module. For instance, assuming a maximal sparsity
threshold of 50%, one writes:
Module_Sparsity < 0.5
(4)
An outlier is a 1-valued matrix element in the
Modularity Matrix outside of any of the diagonal
blocks. Outliers are coined interferences in the
Conceptual Lattice domain (Lindig, 1997). Outliers
cause an undesirable coupling between modules.
The outcome of this coupling is a much larger
coupled diagonal block made of:
• The joint original diagonal blocks coupled by
the outliers;
• A few 1-valued matrix elements outside the
original blocks – the coupling outliers;
• Many zero-valued matrix elements surrounding
the outliers.
The resulting larger coupled diagonal block has
a much lower cohesion than the original modules
coupled by the outlier (see Fig. 3).
Figure 3: Block-diagonal Modularity Matrix with coupling
outlier – There are 5 original modules (marked by blue
background), all of them with high cohesion (i.e. low
sparsity). The outlier couples modules 1 and 2. Around the
outlier there are mostly zeros, causing high sparsity (i.e.
low cohesion) of the coupled joint module of 1 and 2.
ICSOFT-PT2015-10thInternationalConferenceonSoftwareParadigmTrends
112

Searching for outliers, outside the original
modules, the inequality sign is inverted, as the
sparsity is above the threshold:
Outlier_Sparsity_Criterion > 0.5
(5)
The TotalNumElements (total number of
elements) of a block in the Modularity Matrix is the
square of NumStructors, (number of structors). The
NumZeros (number of zero-valued matrix elements)
equals the TotalNumElements minus NumOnes
(number of 1-valued matrix elements). Substituting
these terms in equations (3) and (5), one finally gets
the Outlier Sparsity Criterion for the presence of
outliers in a coupled module of a Modularity Matrix:
Outlier_Sparsity_Criterion =
0.5 * (NumStructors)
2
- NumOnes > 0
(6)
4.4 Modularity Lattice Outliers
Criterion
To find the equivalent Outlier Sparsity Criterion for
a Modularity Lattice, we use the same previous
equation, substituting it with Lattice quantities:
Theorem 2: Modularity Lattice Outliers
Criterion
Given equation (6) for a Modularity Matrix, the
equivalent Outlier Sparsity Criterion for a
Modularity Lattice module containing outliers is
Outlier_Sparsity_Criterion =
0.5 * (NumAttributes)
2
- NumOnes > 0
where
NumOnes = LocalPairs + EdgePairs.
LocalPairs is the number of nodes in which there
are both an attribute and its object locally.
EdgePairs is the number of edges below each
attribute node needed to reach each of its objects,
down to the lowest object, above the Bottom.
Proof outline:
Given equation (6) above, then:
NumAttributes (Number of attributes) in a module is
trivially equal to NumStructors (Number of
structors). NumOnes (Number of 1-valued matrix
elements) is the number of links between attributes
(structors) and objects (functionals). These are of
two Attribute-Object Pair types: a- Local – both in
the same node; b- Edge – in different nodes linked
by edges. Thus, one only needs to count and sum
correctly both types of Attribute-Object pairs.
To illustrate the calculation of quantities
appearing in Theorem 2, we take the simple example
of the Command design pattern middle module. By
the Modularity Lattice in Fig. 2, the number of
Attributes is 3 (Client, Invoker and History). The
first term of the r.h.s. of the equation in Theorem 2
is half the square of NumAttributes, i.e. 4.5. The
second term NumOnes equals 5 which is the sum of
2 LocalPairs (Client/CreateObjs and History/Undo)
and 3 EdgePairs (edges from Invoker-to-Undo,
Invoker-to-Set-Receiver and Client-to-Set-
Receiver). As the Outlier_Sparsity_Criterion is
negative, there is no outlier in this module.
This calculation is totally equivalent to equation
(6). By the Modularity Matrix middle module in Fig.
1, the number of Structors is also 3 (Client, Invoker
and History). Half the square of NumStructors is
4.5. By directly counting the number of ones in the
middle module in Fig. 1, NumOnes equals 5. The
conclusion is the same: no outliers in this module.
5 HEURISTICS FOR
DECOUPLING
Once outliers were pointed out in a system design,
software engineers should apply their ingenuity to
solve the coupling problems and improve the design.
A heuristic rule suggests a decoupling starting
point. This rule is alternatively formulated either in
terms of the Modularity Matrix or in terms of the
Modularity Lattice.
Decoupling Heuristic Rule
Modularity Matrix version
Start decoupling with a row/column with a large
number of 1-valued (outlier) matrix elements.
Modularity Lattice version
Start decoupling with a Lattice node with a large
number of edges to other nodes.
In order to systematically eliminate outliers in a
Modularity Lattice, one should look first for the
node with a maximal connectivity to other nodes.
Then look for the next node in terms of connectivity,
and so on. Following the heuristic rule, a way to deal
with an outlier node coupling of potential modules
in the Modularity Lattice, is to erase a minimal
number of edges from the outlier node and see
whether this reduces the lattice to a modular one.
6 CANONICAL CASE STUDIES
Here we look at software systems case studies,
which are canonical from a modularity viewpoint.
These case studies have been analysed earlier,
LinearSoftwareModels:EquivalenceofModularityMatrixtoItsModularityLattice
113

(Exman, 2014), but here we show the equivalence of
the Modularity Matrix to the respective Lattice.
6.1 The Observer Design Pattern
The Observer design pattern is taken from the GoF
book (Gamma, 1995). Its well-known purpose is a
many-following-one behavior, viz. many observers
change according to the changes in the one subject.
Figure 4: Observer Design Pattern Modularity Matrix.
There are 8 structors and functionals in this matrix.
These form 5 modules (in blue background): a-
upper-left subject role; b- middle observer role; c-
lower-right three strictly diagonal modules: specific
application GUIs and initiator.
The Observer structors are (abstract/concrete)
subject and observer, (analog/digital) clock
application GUI (Graphical User Interface), a
subject resource (the internal clock) and an initiator
to construct objects. The pattern functionals include
the clock application Display “digital” and “analog”.
The Observer Modularity Matrix in Fig. 4 shows
a perfect block-diagonal modularity. The upper left
block is the subject. The middle block is the
observer. The lower right structors refer to
application specific GUI and the initiator. The
corresponding Modularity Lattice is seen in Fig. 5,
following, from left to right, Module types 1c, 1b
and 1a of the Corollary in sub-section 4.2.
6.2 The Parnas KWIC System
Parnas described in his seminal paper (Parnas, 1972)
the KWIC system for producing an index containing
sentences circular shifted through all possibilities,
keeping word order, and alphabetically sorted.
KWIC illustrated the idea of modularity. Two
modularizations were suggested: one with couplings
and another with couplings resolved.
The KWIC system 1
st
modularization illustrates a
coupling case, seen in the Modularity Matrix in Fig.
6. Its matching Lattice is in Fig. 7. Both
representations lead to the same conclusions.
The Parnas 1
st
Modularity Matrix of the KWIC
Figure 5: Observer Design Pattern Modularity Lattice –
There are 5 modules in this lattice: a- l.h.s. with 3
attributes (Subject, Concrete Subject, Subject Resource) is
the Subject Role; b- middle with 2 attributes (Concrete
Observer, Observer) is the Observer Role; c- r.h.s. with 3
modules, each with just 1 attribute (two GUIs and one
Init). Modules correspond to the matrix in Fig. 4.
Figure 6: Parnas KWIC System 1
st
Modularization Matrix
– This Modularity Matrix shows coupling between two
potential modules (marked by light blue background). The
coupling outliers (marked by hatched background) are in
column S3 (the Master Control) and in row F3.
system in Fig. 6 points to two couplings (with a
hatched background): a- the Master Control is not a
real sub-system, as it refers to all functionals (a
whole column S3 of 1-valued matrix elements); b-
the “Store line in word order” functional in row F3
is a coupling of any two potential modules (marked
by a blue background).
The Parnas KWIC 1
st
modularization Modularity
Lattice in Fig. 7 points to exactly the same couplings
as its Modularity Matrix: a- The Master Control is
indeed not a real sub-system, as it appears at the Top
(its extent is all the 5 objects!); b- The node of the
“Stores line in word order” has no proper attribute
and it couples every attribute, except Output;
The solution of the above coupling problems is to
eliminate the Master Control from the system
composition as it is not a sub-system and add a new
“Line Storage” structor (attribute), to which all the
ICSOFT-PT2015-10thInternationalConferenceonSoftwareParadigmTrends
114

Figure 7: Parnas KWIC System 1
st
Modularization Lattice
– Two modules are apparent in this lattice: a- l.h.s. with 4
attributes (Circular Shifter, Alphabetizer, Input, Master
Control); b- r.h.s. with 2 attributes (Output, Master
Control). The Master Control couples the 2 modules. The
“Stores Line in word order” object is also coupling the
l.h.s. module. This Lattice matches the matrix in Fig. 6.
other structors refer for “Storing line in word order”.
The outcome fits Parnas KWIC 2
nd
modularization which is indeed canonical. It is a
strictly diagonal Modularity Matrix, and a matching
Lattice with five neat single node modules.
7 REAL SYSTEM CASE STUDY
7.1 The NEESGrid System
This system, developed at the NCSA at Urbana,
Illinois, enables a “Network Earthquake Engineering
Simulation” – for details see (Finholt 2004).
The system Modularity Matrix is in Fig. 8. It
has three diagonal blocks. The top-left module refers
to Data as seen by structor and functional names.
The middle module refers, by the functionals with
Col suffix, to collaboration types, viz. synchronous,
asynchronous and other. The right bottom strictly
diagonal elements are external modules.
Figure 8: NEESGrid System Modularity Matrix – shows
coupling mainly between two 3*3 modules (with light
blue background). The coupling outliers (with hatched
background) are in column S4 (DataAc) and in row F4
(OtherCol).
Of the 3 outliers (with hatched background)
close to the block borders, two of them are in the
OtherCol row F4 and the third one in the DataAc
column S4, pointing out to specific couplings.
7.2 The NEESGrid Modularity Lattice
There is a clear matching between the NEESGrid
Modularity Matrix in Fig. 8 and its Lattice in Fig. 9.
Figure 9: NEESGrid Modularity Lattice – The three
groups of modules here are: a- the left group containing 3
one-attribute modules (DataDis, HybExp, SimRep); b- the
middle module with Col objects (SyncCol, AsynCol,
OtherCol); c- the right group with Data Attributes/Objects
(DataVu, DataRp, Data Str). OtherCol and DataAc are
couplings between the second and third modules.
The Modularity Lattice has 3 left-most paths
with just 1 node in each path, fitting the Modularity
Matrix purely diagonal elements.
The right-most group of modules in the
Modularity Lattice referring to Data, with attributes
DataVu, DataRp, DataStr, fits the Modularity Matrix
top-left module. The middle group of modules in the
Modularity Lattice refer to collaborations (Col)
having three objects SyncCol, AsyncCol, OtherCol.
But, these right-most and middle groups of
modules are coupled. This can be checked by
computing the Outlier Sparsity Criterion for these
coupled Modularity Lattice modules (from Theorem
2 in sub-section 4.4), which is 10.5. It is bigger than
zero thus there are outliers in these coupled modules.
The node with the OtherCol object has no
attribute by itself and is the most linked node in the
Lattice, thus a good starting point for decoupling
analysis. This agrees with the Modularity Matrix,
OtherCol F4 row with maximal outlier number.
Both representation analyses lead to the same
potential modules, and the same suspect outliers.
LinearSoftwareModels:EquivalenceofModularityMatrixtoItsModularityLattice
115

8 DISCUSSION
This work has shown by theoretical arguments and
case studies, the equivalence between two different
modularity representations of a software system, viz.
the Modularity Matrix and its Modularity Lattice.
This is interesting as it mutually reinforces their
independent conclusions, and it triggers new
questions in each representation, motivated by the
line of thoughts of the other one.
In practical terms, both representations enable to
assess modularity of a software system and to
highlight localized couplings deserving software
sub-system redesign.
8.1 Future Work
Concerning rigorous formalization, linearity still is
an open issue worth of investigation in the context of
Modularity Lattices. Moreover, is there any meaning
to non-linearity for software systems?
In the context of Modularity Matrices, we have
asked whether systems with outliers like the
NEESGrid system, are amenable to complete block-
diagonalization or they are essentially non-block-
diagonal. Are these systems the exception, or a class
on their own? The equivalence of Modularity
Matrices and Lattices should facilitate research.
REFERENCES
Baldwin, C.Y. and Clark, K.B., 2000. Design Rules, Vol.
I. The Power of Modularity, MIT Press, MA, USA.
Belohlavek, R., 2008. Introduction to Formal Concept
Analysis, Dept. of Computer Science, Palacky
University, Olomouc, Czech Republic.
Cai, Y. and Sullivan, K.J., 2006. Modularity Analysis of
Logical Design Models, in Proc. 21
st
IEEE/ACM Int.
Conf. Automated Software Eng. ASE’06, pp. 91-102,
Tokyo, Japan.
Concept Explorer, 2006 – Web site:
http://conexp.sourceforge.net/. Visited May 2015.
Exman, I., 2012. Linear Software Models for Well-
Composed Systems, in S. Hammoudi, M. van
Sinderen and J. Cordeiro (eds.), 7
th
ICSOFT’2012
Conf., pp. 92-101, Rome, Italy.
Exman, I., November 2012. Linear Software Models,
Extended Abstract, in I. Jacobson, M. Goedicke and P.
Johnson (eds.),. GTSE 2012, SEMAT Workshop on
General Theory of Software Engineering, pp. 23-24,
KTH Royal Institute of Technology, Stockholm,
Sweden,. See also video presentation:
http://www.youtube.com/watch?v=EJfzArH8-ls.
Exman, I., 2013. Linear Software Models are Theoretical
Standards of Modularity, in J. Cordeiro, S.
Hammoudi, and M. van Sinderen (eds.): ICSOFT
2012, Revised selected papers, CCIS, Vol. 411, pp.
203–217, Springer-Verlag, Berlin, Germany. DOI:
10.1007/978-3-642-45404-2_14.
Exman, I., 2014. Linear Software Models: Standard
Modularity Highlights Residual Coupling, Int. Journal
on Software Engineering and Knowledge Engineering,
vol. 24, pp. 183-210, March 2014. DOI:
10.1142/S0218194014500089.
Finholt, T.A., Horn, D. and Thome, S., 2004. NEESgrid
Requirements Traceability Matrix, Technical Report
NEESgrid-2003-13, University of Michigan.
Gamma, E., Helm, R., Johnson, R. and Vlissides, J., 1995.
Design Patterns: Elements of Reusable Object-
Oriented Software, Addison-Wesley, Boston, MA.
Ganter, B. and Wille, R., 1999. Formal Concept Analysis.
Mathematical Foundations. Springer.
Ganter, B., Stumme, G. and Wille, R., 2005. Formal
Concept Analysis - Foundations and Applications.
Springer.
Heckmann, P. and Speicher, D., 2012. Assisted Software
Exploration using Formal Concept Analysis”, in
SKY’2012 3
rd
Int. Workshop on Software Knowledge,
pp. 11-21, SciTePress, Portugal.
Lindig, C. and Snelting, G., 1997. Assessing Modular
Structure of Legacy Code Based on Mathematical
Concept Analysis, in ICSE’97 Proc. 19
th
Int. Conf. on
Software Engineering, pp. 349-359, ACM. DOI:
10.1145/253228.253354.
Parnas, D.L., 1972. On the Criteria to be Used in
Decomposing Systems into Modules, Comm.. ACM,
15, 1053-1058.
Siff, M. and Reps, T., 1999. Identifying modules via
concept analysis, IEEE Trans. Software Engineering,
Vol. 25, (6), pp. 749-768. DOI: 10.1109/32.824377.
Snelting, G., 2000. Software reengineering based on
concept lattices, in Proc. of 4
th
European Software
Maintenance and Reengineering, pp. 3-10, IEEE.
DOI: 10.1109/CSMR.2000.827299.
Steward, D., 1981. The Design Structure System: A
Method for Managing the Design of Complex
Systems, IEEE Trans. Eng. Manag., EM-29 (3), pp.
71-74.
Wille, R., 1982. Restructuring lattice theory: an approach
based on hierarchies of concepts. In: I. Rival (ed.):
Ordered Sets, pp. 445–470, Reidel, Dordrecht-Boston.
ICSOFT-PT2015-10thInternationalConferenceonSoftwareParadigmTrends
116
