Spatio-Temporal Normalization of Data from Heterogeneous Sensors

Alessio Fanelli, Daniela Micucci, Marco Mobilio and Francesco Tisato

Department of Informatics, Systems and Communication University of Milano - Bicocca, Milan, Italy

Keywords:

Sensor Heterogeneity, Modularisation, Software Architecture, Knowledge Representation.

Abstract:

The growing use of sensors in smart environments applications like smart homes, hospitals, public transporta-

tion, emergency services, education, and workplaces not only generates constantly increasing of sensor data,

but also rises the complexity of integration of heterogeneous data and hardware devices. In order to get more

accurate and consistent information on real world events, heterogeneous sensor data should be normalized.

The paper proposes a set of architectural abstractions aimed at representing sensors’ measurements that are

independent from the sensors’ technology. Such a set can reduce the effort for data fusion and interpretation.

The abstractions allow to represent raw sensor readings by means of spatio-temporal contextualized events.

1 INTRODUCTION

Smart environments are usually instrumented with

various typologies of sensors. Sensors may have a

ﬁxed position, like a thermometer or a light sensor,

or they may move inside the environment, like the

sensors embedded in smartphones. Moreover, sen-

sors are heterogeneous, thus producing measurements

that are semantically linked to their sources. Appli-

cations that rely on sensors’ measurements usually

fall under the umbrella of Ambient Intelligence (AmI)

that includes speciﬁc domains like smart homes,

health monitoring and assistance, hospitals, trans-

portation, emergency services, education, and work-

places (Cook et al., 2009). Such applications often are

required to know the speciﬁc device that originated

the measurement in order to understand and use the

information provided. This leads to vertical systems,

which feature low modularity and scarce openness.

When modeling sensors and related measure-

ments, architectural solutions should face the chal-

lenge related to both heterogeneity and semantics. For

example, authors in (Widyawan et al., 2012) propose

a layered architecture that provides the low-level soft-

ware, the middleware, and the upper-level services

with detailed speciﬁcations of the involved sensors.

This way sensors are well modeled, but their knowl-

edge is distributed throughout all the system. Authors

in (Dasgupta and Dey, 2013) focus on issues related

to the management of large amount of data from sen-

sors: the proposed approach consists in transforming

sensor data in what authors call a set of observations

that are meaningful for the applications. Lower lev-

els embed semantics that is strictly related to the spe-

ciﬁc application. This lead to scarce reusability as the

same abstraction rules for a speciﬁc sensor may not

be applicable in different contexts. Finally, database

approach is growing interest. Indeed, the database ap-

proach allows heterogeneous applications to access

the same sensor data via declarative queries. This

kind of solutions may resolve data heterogeneity at

the application level, but there still persists the issue

of sensor data management, since most of the exist-

ing solutions suppose homogeneous sensors generat-

ing data according to the same format (Gurgen et al.,

2008).

The identiﬁcation of a suitable set of architec-

tural abstractions, able to represent sensor measure-

ments independently from the hardware characteris-

tics of the source, could improve reusability, open-

ness, and modularity of software systems. These

abstractions allow to remove the dependency from

the sensor by contextualizing the measurements in

a spatio-temporal frame. Measurements result in

spatio-temporal events that can be stored inside a

Data Base Management System (DBMS) or streamed

inside a Data Stream Management System (DSMS)

(Motwani et al., 2002), as proposed in (Gurgen et al.,

2008). The main beneﬁt is that applications no longer

need to know the kind and the numbers of deployed

sensors. Upon the occurrence of an event of interest,

applications can decide to access all the other events

that are related both spatially and temporally. In this

paper neither the storage nor distribution of data is

462

Fanelli A., Micucci D., Mobilio M. and Tisato F..

Spatio-Temporal Normalization of Data from Heterogeneous Sensors.

DOI: 10.5220/0005559504620467

In Proceedings of the 10th International Conference on Software Engineering and Applications (ICSOFT-EA-2015), pages 462-467

ISBN: 978-989-758-114-4

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

handled, but the focus is on the deﬁnition of such a

set of architectural abstractions that could solve sen-

sors heterogeneity issue, in order to be able to apply

one of the mentioned approaches for data distribution,

storage, and usage.

This paper will present the basic concepts along

with the following simpliﬁed case of study. Con-

sider a smart building composed by different rooms;

in each room different sensors are located. In our ex-

ample, we consider a room only (room1) that is in-

strumented as follow: in the top corner there is a cam-

era (cam1) facing the centre of the room. Hanged on

the wall there is also a thermometer (therm1). More-

over, a person in the room owns a smartphone with the

accelerometer acc1. In this kind of contexts, smart-

phones are usually considered as extensions of the

user, which means that their position is the same. Sev-

eral applications can rely on the above listed sensors:

a tracking application could try to follow the user (ei-

ther a speciﬁc one or any user) and could make the

position available to the system; an application could

exploit the locations of the users to control the temper-

ature in the rooms accordingly, based on their needs

or preferences. These are just a few examples that can

beneﬁt from the proposed approach.

The rest of this paper is organized as follow: Sec-

tion 2 introduces the basic concepts used to model

spatial contextualization; Section 3 presents the pro-

posed abstractions; ﬁnally Section 4 sketches some

ﬁnal remarks about the ongoing work and provides

details about the future directions.

2 BACKGROUND CONCEPTS

Spatial contextualization has been derived from con-

cepts deﬁned in (Tisato et al., 2012; Micucci et al.,

2014) and that will be summarized in the following.

A space is a set of potential locations, that are all

the locations that could be theoretically considered in

that space. For example, in a graph the potential loca-

tions are all the nodes. On the other hand, if a Carte-

sian space is used to localize entities within a room,

then the potential locations are every point in R

the area delimited by the room perimeter. Applica-

tions explicitly manage effective locations, which are

a subset of space’s potential locations. For example,

an application that calculates the trajectory of a mo-

bile entity will only explicitly consider a ﬁnite number

of locations in the Cartesian space, that is, the loca-

tions belonging to the trajectory.

A zone C

is a subset of potential locations of a

space S. It is deﬁned by a set of effective locations

termed characteristic locations in S and by a member-

ship function that states if a given location of S be-

longs to the zone. Essentially, the membership func-

tion is a boolean function that is true when a loca-

tion falls within the zone. According to the member-

ship function used, different kinds of zones can been

identiﬁed, such as: enumerative, premetric declara-

tive, polygonal, and pure functional. We focus on the

pure functional type. Figure 1 shows the concepts of

space, zone, location and membership function.

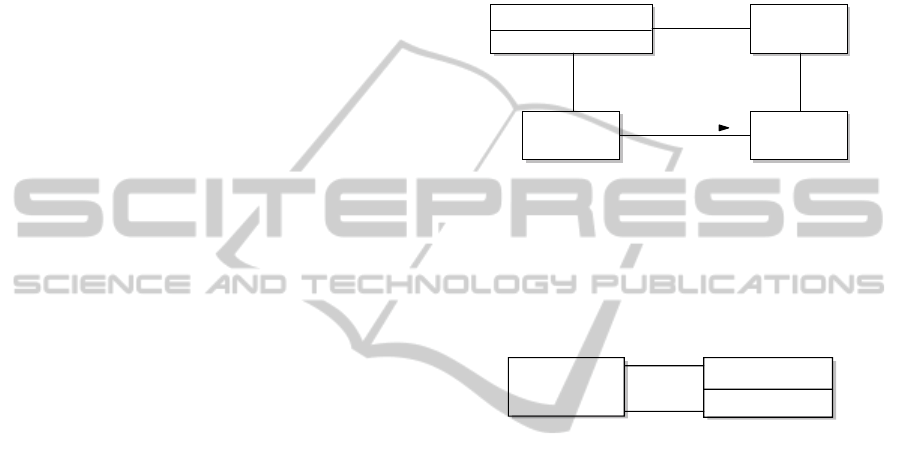
Zone

MembershipFunction

+ belongsTo(location) :boolean

Location

Space

+effective 1..*

+characteristic

defined over

Figure 1: Space, Location, and Zone.

Given two different zones, a mapping relation is

a generic function deﬁned in C

− > C

(where S

and S

are spaces, and C

and C

are zones deﬁned

on those spaces respectively). Thus it can be seen as

a mapping between zones in different spaces.

Space MappingRelation

+ map(Zone) :Zone

+source

+reference

Figure 2: Mapping Relation.

Figure 2 pictures the concept of mapping relation

with one of the spaces acting as reference space, so it

can be seen in a hierarchical fashion with hierarchies

of spaces mapped through mapping relations.

3 THE MODEL

Measurements from sensors can be modeled as data

contextualized in a spatial-temporal context. Time

contextualization is not detailed here for shortness.

Concepts related to time and to clocks synchroniza-

tion can be found in (Fiamberti et al., 2012). Before

describing the model in detail, an overall presentation

will be provided.

3.1 General Overview

The approach proposes an abstraction process able to

produce spatio-temporal contextualized events, start-

ing from low level measurements that are strictly sen-

sor dependant.

Figure 3 provides a graphical representation of the

identiﬁed abstractions: at the bottom level there are

Spatio-TemporalNormalizationofDatafromHeterogeneousSensors

463

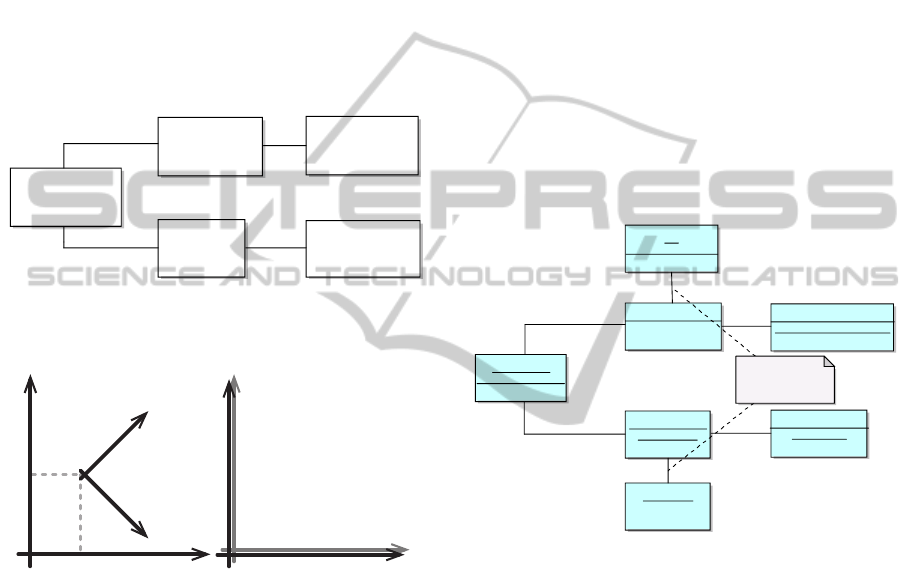
Sensor

Data

Normalized Stimuli Level

Stimuli Level

Signals

Applications

Time

Data

Zone

Space

Figure 3: Abstractions.

physical sensors, which are considered outside the

system. Sensors produce signals that are here in-

tended as raw samplings. Raw sampling is then ab-

stracted into stimuli, which are the lower level infor-

mation the system receives and that is strictly related

to its hardware source. In Figure 3, stimuli are de-

picted at the stimuli level and are represented by data

associated to sensors. At the normalized stimuli level,

stimuli are contextualized both spatially and tempo-

rally and are denoted normalized stimuli. For spatial

contextualization we intend that the stimulus (data in

Figure 3) has associated a zone in a space that models

the physical environment. For temporal contextual-

ization we intend that all the stimuli have associated a

time value that is related to the same clock. This way,

all the stimuli are contextualized in the same refer-

ence frames (time and space) and can be viewed by

the applications as events occurred in speciﬁc places

in the physical environment at speciﬁc time instants

relieving them by low level and hardware dependent

details.

3.2 Sensors

Sensors are the meta representation of the physical

sensors; they are in charge of acquiring signals and

providing stimuli. As shown in Figure 4, sensors are

localized in a physical space (PhysicalSpace)

through a physical zone (PhysicalZone).

PhysicalSpace and PhysicalZone are special-

ization of Space and Zone respectively as deﬁned in

(Tisato et al., 2012; Micucci et al., 2014).

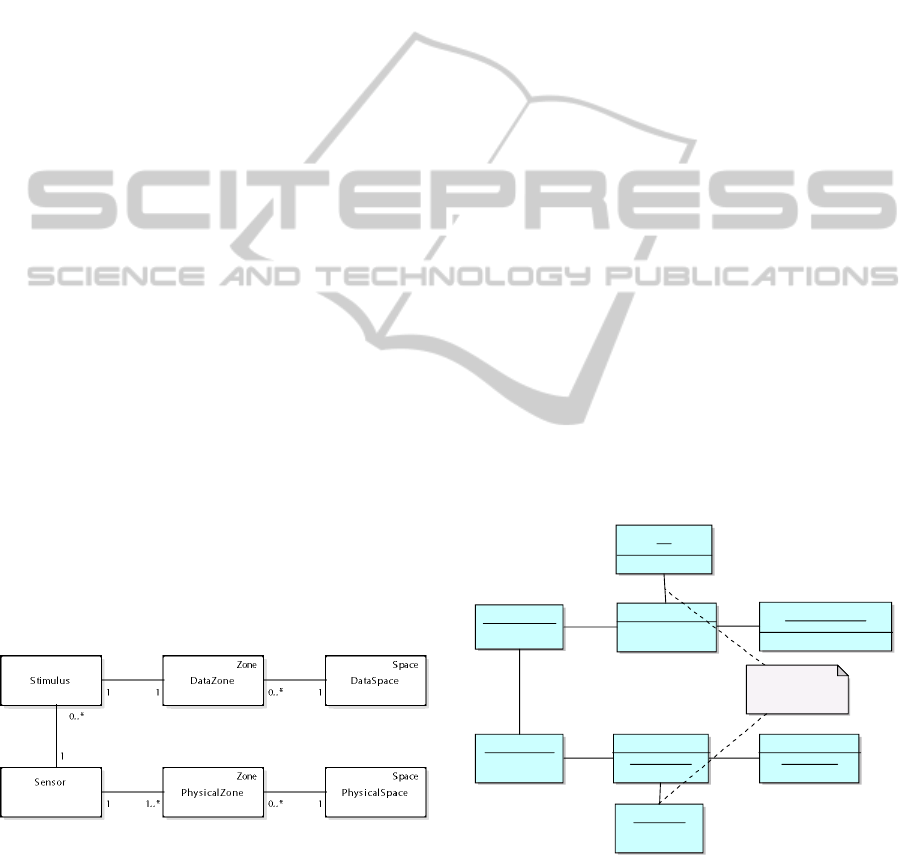
Stimulus

Sens or

Zone

Phys icalZone

Space

Phys icalS pace

Zone

DataZone

Space

DataSpace

0.. *

1 1.. * 0.. * 1

1 1 0.. * 1

Figure 4: A sensor and its physical localization.

A physical space is a space that models the ac-

tual physical world; it is used to localize entities (and

events also). A special class of entities are the sen-

sors.

Localization means placing an entity in a well de-

ﬁned position inside the physical space. This can be

achieved by using zones as deﬁned in (Tisato et al.,

2012; Micucci et al., 2014) and introduced in Section

2. This may sufﬁce when the orientation of a sensor

does not affect the interpretation of the acquired val-

ues. For example, the measurements of a temperature

sensor are not affected by the orientation of the sensor

itself. On the other hand, such a deﬁnition may be too

poor. For example, consider a physical space as rep-

resented by a Cartesian 3D space with locations mod-

eled as a triple (x, y, z). A camera may be localized

through a zone that includes a characteristic location

with values for x, y, and z equal to the real position

in the world. Such localization is not sufﬁcient to in-

terpret the acquired frames as the orientation is also

required. To fulﬁll this need, the concept of oriented

physical zone has been introduced as a specialization

of the physical zone, that also features the orientation,

in order to give a more consistent representation of a

position within a physical space.

Both physical space and corresponding locations

are specialized in order to model speciﬁc spaces ty-

pologies (e.g., 3D Cartesian, 2D grid, and so on) and

location typologies (e.g., a point in a 3D cartesian

space, a cell in a 2D grid, and so on). Zones are

not specialized because what characterizes a zone is

its membership function that can model, for instance,

cones, discretized spheres, and so on.

Considering the scenario introduced in Section 1,

room1 is represented by a 3D Cartesian space (a phys-

ical space). Suitable locations for this kind of space

are 3D points. Several kind of physical zones can be

deﬁned over this space: single location zone, single

location oriented zone, cone zone, sphere zone. Ther-

mometer therm1 is localized inside room1 by means

of a physical zone constituted by a single location

that sufﬁces to physically localize the acquired stim-

uli. Being sensor therm1 in position (0.3, 0.4, 0.1),

then, the characteristic location of its physical zone is

a 3D point with values [0.3, 0.4, 0.1] (see Figure 5).

therm1 :Sensor therm1PhysicalZone :

PhysicalZone

room1PhysicalSpace :

Cartesian3D

p1 :Point3D

indirect via Membership

function

Figure 5: Therm1 physical localization.

Camera cam1 has similar features: its position is

an oriented physical zone that represents the corner of

the room where it is ﬁxed and the fact that is facing

the center of the room. Finally, accelerometer acc1

ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications

464

inside the smartphone is associated with the oriented

physical zone occupied by the smartphone itself. In

this case, the orientation represents how the smart-

phone is placed with respect to the room space, such

information is fundamental in order to correctly inter-

pret acc1’s data in most of domain applications (such

as dead reckoning).

3.3 Stimuli

Signals are raw data sensed (and usually sampled) by

sensors. Physical sensors emit signals, which are usu-

ally in form of voltages values. These signals are then

translated into stimuli through well-known conversion

functions. As an example, a simple temperature probe

is physically designed to output a voltage signal that

is linearly proportional to the local temperature. In

this example, the conversion function is the expres-

sion that maps such voltage readings into values that

represent the temperature in degrees.

Stimuli are referred to the sensor that produced

them and they are contextualized in zones (data

zones) of a speciﬁc space “owned” by the sensor: the

data space. A data space represents the admitted val-

ues for the sensor’s stimuli. For example, the data

space of an accelerometer is a 3D Cartesian space,

where the axes represent the ones of the acceleration

data and are in m/s

. It could have, as an example, a

valid range of + or - 4g. Locations in that space are

triples of values.

Data zones are simply zones deﬁned in data

spaces. For example, a stimulus from an accelerom-

eter is located in a data zone whose characteristic lo-

cation is a location whose values corresponds to the

value read for each axis. If the stimulus is [x=0, y=1,

z=1], then the characteristic location of the data zone

is exactly [x=0, y=1, z=1].

Figure 6: Stimulus.

Figure 6 depicts the stimulus. It is associated to

the sensor that acquired its corresponding signal and

it is spatially contextualized by means of a data zone

(whose value equals the value of the sample) in the

sensor data space. Being data space a specialization

of space, it can be specialized like the physical zone to

represent different kind of data space (e.g., Fahrenheit

space, Celsius space, accelerometer space, and so on).

The same holds for its locations.

It is worth noting that the distinction between

physical space and data space and between physical

zone and data zone is purely conceptual: they are all

spaces and zones respectively as deﬁned in (Tisato

et al., 2012; Micucci et al., 2014).

In the example scenario previously introduced,

there are three different types of stimuli. A sample

from therm1 is pictured in Figure 7. Sensor therm1

generates stimuli in a Celsius format. Thus, the sensor

data space is a Celsius temperature space that repre-

sents the space of the temperature readings by therm1

and whose locations are simply values in the scale (-

40 +40). A data zone for this kind of space includes a

membership function with associated one character-

istic location only. Suppose that therm1 acquires a

stimulus with value 23 Celsius Degree, then the l1

value is 23. Moreover, the stimulus temp1 is associ-

ated to therm1 sensor so that the information related

to the position of the sensor can be obtained.

A stimulus from cam1, instead, is localized via a

data zone in a image data space that represents the

space of the frames acquirable from cam1. The zone

has associated a set of locations that corresponds to

the matrix of the sensed image. Moreover, it is asso-

ciated the sensor cam1. Finally, an acceleration stim-

ulus from acc1 is localized in a data zone whose as-

sociated location corresponds to the sensed acceler-

ation. Such a zone is deﬁned on a acceleration data

space that is a three dimensional space. Moreover, it

is associated to the sensor acc1.

temp1 :Stimulus

therm1 :Sensor

tempNZone :DataZone

therm1PhysicalZone :

PhysicalZone

l1 :

TemperatureLocation

indirect via Membership

function

room1PhysicalSpace :

Cartesian3D

p1 :Point3D

thermDataSpace :

FahrenheitTemperatureSpace

Figure 7: Stimulus Example.

3.4 Normalized Stimuli

A normalized stimulus is a further abstraction of a

stimulus and is depicted in Figure 8. It represents the

sensed value from a sensor that is spatially and tem-

Spatio-TemporalNormalizationofDatafromHeterogeneousSensors

465

porally contextualized and that is unrelated from the

sensor that produced it.

The normalization process takes into account the

physical position of the sensor and its characteristics,

in order to provide a physical zone in which the stim-

ulus is located and that is referred to the same phys-

ical space in which the source sensor is immersed.

Moreover, a normalized stimulus is located through

a normalized data zone in normalized data space. For

example, imagine that there are different temperature

sensors: some of them acquires in Celsius and others

in Fahrenheit. A normalized data space in this case

can be a Celsius data space in which localizing all the

temperatures.

Data

NormalizedStimulus

DataZone

NormalizedDataZone

DataSpace

NormalizedDataSpace

Space

PhysicalSpace

Zone

PhysicalZone

Figure 8: Normalized Stimulus.

More complicated situations may occur.

Room PhysicalSpace

Sensor

Accelerometric DataSpace

(a)

Room

Accelerometric DataSpace

Room PhysicalSpace

(b)

Figure 9: Physical and Data Spaces relationships.

For example, Figure 9 shows the different rela-

tionships between a speciﬁc sensor’s data space, and a

normalized data space associated with a more broaden

and generic sensor. The room physical space repre-

sents the physical space of the room in which the sen-

sor is positioned (and oriented), while the sensor ac-

celerometric data space represents the data space of

the accelerometer values. As shown in Figure 9a, the

two spaces are not aligned: in this example an ori-

ented physical zone is required to consistently repre-

sent the position of the accelerometer inside the room

physical space. The orientation of the sensor will be

used as a parameter by the mapping relation function

that will translate the starting data zone into its nor-

malized counterpart, which will be related to the room

accelerometeric data space shown in Figure 9b. For

example, if the sensor is in the position showed in Fig-

ure 9a, the gravitational acceleration would be sensed

among both the axes of the sensor, while the normal-

ized value would only feature a −1g on the y axis.

Considering the example scenario, the previ-

ously deﬁned temp1 stimulus depicted in Figure

7 was contextualized inside the thermDataSpace

data space and was expressed in Celsius degrees.

The corresponding normalized stimulus, as pic-

tured in Figure 10 will be contextualized inside the

tempNormalizedDataSpace, which, in this scenario

contains temperature readings in Fahrenheit degrees,

giving a good example of data zone normalization

in order to be globally consistent with all the other

homogeneous information source inside the room.

Moreover the normalized stimulus is localized inside

the physical space of room1 (room1PhysicalSpace).

Since the sensor was not oriented and its data has no

particular positioning, the position of the sensor and

of the normalized stimulus are in this case equivalent.

Temp1Norm :

NormalizedStimulus

tempNZone :DataZone

temp1NormZone :

PhysicalZone

room1PhysicalSpace :

Cartesian3D

tempNormalizedDataSpace :

CelsiusTemperatureSpace

p2 :Point3D

Indirect via Membership

function

l2 :

TemperatureLocation

Figure 10: Normalization Example.

The stimulus from cam1 needs a bit more of com-

putation in normalizing the oriented physical zone of

cam1 into the non-oriented physical zone in which the

normalized stimulus will be located. While the ﬁrst

represents the position of the camera (a single point,

or a small well deﬁned region of the physical space)

and its orientation, the latter in order to be represen-

tative for the normalized stimulus must represent the

physical cone viewed by cam1.

The normalization of the accelerations is similar

to the temperatures: the acceleration data zone, re-

ferred to the acceleration data space is normalized and

become a normalized acceleration zone in the room1

accelerations data space (i.e., the data space in which

all of the accelerations sensed in the room are contex-

tualized). The acceleration is also enriched with its

physical zone, which is a non-oriented physical zone

derived from the oriented physical one of acc1.

ICSOFT-EA2015-10thInternationalConferenceonSoftwareEngineeringandApplications

466

3.5 Data Flow

In Section 3.3 and 3.4 stimuli and normalized stimuli

have been deﬁned. This subsection deals with how

those normalization happens. In Section 2 the concept

of mapping relation has been introduced: normalizing

a physical zone into another physical zone can be triv-

ial or quite complex depending on the nature of the

data, but it should always be a repeatable and deter-

ministic process, which means that it is possible to de-

ﬁne a mapping function that relates any physical zone

into a corresponding physical zone in the reference

space. As already mentioned, the difference between

data and physical is purely logical, so it is reasonable

to say that data zones are normalized accordingly; it is

nonetheless noteworthy that a mapping relation could

easily need further information about the zones that

need to be normalized.

Using mapping relations in order to remove any

relationship between a sensor and the data it produces

allows to obtain homogenous data, resolving one of

the main issues of sensor heterogeneity.

Consider the acceleration previously deﬁned and

normalized in the reference scenario. The physical

normalization is trivial and only consists in contex-

tualizing the stimulus in the non-oriented part of the

acc1 physical zone. The data zone conversion in-

stead, must use the orientation from the physical zone

of acc1 in order to normalize the acceleration from

the accelerations data space of acc1 to the room1 ac-

celerations data space that is jointly placed with the

room1 physical space: this means that, apart from

the usual conversions of scales and measurement unit,

a roto-translation of the acceleration is needed. The

information needed for this particular transformation

is the orientation of the accelerations data space of

acc1, which directly depends on the orientation of

acc1 itself. This is why acc1 has an oriented physi-

cal zone and its normalized stimuli does not: the ori-

entation has already been taken into consideration for

normalizing the acceleration data.

Similarly, the cam1 stimuli are normalized into

normalized stimuli that feature non-oriented physical

zones. This time the orientation is not used to manip-

ulate the data zone, but it is required, along with other

intrinsic parameters of cam1, to determine the shape,

size and displacement of the cone that represents the

physical zone of each normalized stimulus.

4 CONCLUSIONS

The proposed model has been implemented in a pre-

liminary proof-of-concept Java-based version in order

to test the main ideas. The testing has been conducted

exploiting simulated sensors, in particular accelerom-

eters and thermometers.

While a solid and wider implementation is re-

quired, the approach has proven to be effective and,

in the test case, efﬁcient.

The main future directions include the manage-

ment of other typologies of senors including cameras;

an experimentation with real world sensors; and the

realization of data-ﬂow mechanisms that domain ap-

plications can exploit to access and query normalized

stimuli.

REFERENCES

Cook, D. J., Augusto, J. C., and Jakkula, V. R. (2009).

Ambient intelligence: Technologies, applications, and

opportunities. Pervasive and Mobile Computing,

5(4):277 – 298.

Dasgupta, R. and Dey, S. (2013). A comprehensive sen-

sor taxonomy and semantic knowledge representa-

tion: Energy meter use case. In Sensing Technol-

ogy (ICST), 2013 Seventh International Conference

on, pages 791–799. IEEE.

Fiamberti, F., Micucci, D., Morniroli, A., and Tisato, F.

(2012). A model for time-awareness, volume 112 of

Lecture Notes in Business Information Processing.

Gurgen, L., Roncancio, C., Labb

e, C., Bottaro, A., and

Olive, V. (2008). Sstreamware: a service oriented

middleware for heterogeneous sensor data manage-

ment. In Proceedings of the 5th international con-

ference on Pervasive services, pages 121–130. ACM.

Micucci, D., Vertemati, A., Fiamberti, F., Bernini, D., and

Tisato, F. (2014). A spaces-based platform enabling

responsive environments. International Journal On

Advances in Intelligent Systems, 7(1 and 2):179–193.

Motwani, R., Widom, J., Arasu, A., Babcock, B., Babu, S.,

Datar, M., Manku, G., Olston, C., Rosenstein, J., and

Varma, R. (2002). Query processing, resource man-

agement, and approximation ina data stream manage-

ment system. Technical Report 2002-41, Stanford In-

foLab.

Tisato, F., Simone, C., Bernini, D., Locatelli, M. P., and

Micucci, D. (2012). Grounding ecologies on multiple

spaces. Pervasive and Mobile Computing, 8(4):575–

596.

Widyawan, Pirkl, G., Munaretto, D., Fischer, C., An, C.,

Lukowicz, P., Klepal, M., Timm-Giel, A., Widmer, J.,

Pesch, D., and Gellersen, H. (2012). Virtual lifeline:

Multimodal sensor data fusion for robust navigation in

unknown environments. Pervasive and Mobile Com-

puting, 8(3):388–401.

Spatio-TemporalNormalizationofDatafromHeterogeneousSensors

467