
Global Optimization with Gaussian Regression Under the Finite Number
of Evaluation
Naoya Takimoto and Hiroshi Morita
Department of Information and Physical Sciences,Graduate School of Information Science and Technology,
Osaka University, Suita, Osaka, Japan
Keywords:
Global Optimization, Black-box Function, Bayesian Global Optimization, Kriging, Random Function,
Response Surface, Stochastic Process.
Abstract:
Computer experiments are black-box functions that are expensive to evaluate. One solution to expensive
black-box optimization is Bayesian optimization with Gaussian processes. This approach is popularly used in
this challenge, and it is efficient when the number of evaluations is limited by cost and time constraints, which
is generally true in practice. This paper discusses an optimization method with two acquisition functions. Our
new method improves the efficiency of global optimization when the number of evaluations is strictly limited.
1 INTRODUCTION
Computer models of complex processes are now
ubiquitous in all domains of pure and applied sci-
ences. These models can be viewed as black-box
functions that provide a response to sampled input
values.
Choosing the sampling points in the input space
can be viewed as the design of computer experiments.
Optimal sampling obviously depends on the goal of
the computer experiments. Bayesian global optimiza-
tion methods are useful for this purpose because they
select the next sampling point based on all previous
evaluations.
A statistical model fits the sampled points for fu-
ture predictions and measures the possible predic-
tion error. For data fitting, surrogate models such as
the response surface methodology, kriging, radial ba-
sis functions, splines and neural networks are widely
used. These models replace costly computer models
with simple functions for evaluation.
The kriging method, which uses Gaussian pro-
cess models as response surfaces, was originally pro-
posed for geostatistics research. Optimal solutions are
searched on the response surface, which should there-
fore be well-fitted.
Thus, the kriging method must minimize the inte-
grated mean square error (IMSE) by some technique,
such as finding the sample point that maximizes the
standard error of regression. When the response sur-
face fully traces the objective function, we can obtain
the optimal solution on it.
Although this method can find other local optima,
reducing the IMSE is the sub target in global opti-
mization problems. The main target is improving the
current best solution, which may require exploring
the entire search space, especially the regions of high
uncertainty (i.e., the unknown areas). Such global
searching is called exploration. Because unexplored
regions may be significantly better than any regions
previously searched, exploration reduces the effort
wasted by the algorithm in searching suboptimal re-
gions.
Exploitation refers to the searching of the current
local neighborhood around the current sample-best
solution, where better solutions exist with high proba-
bility. For example, the next sampled point may max-
imize the mean of the regression. This method fre-
quently finds a local rather than the global optimal
solution.
Analogous to the above-mentioned local and
global searching, the main target is to not improve
the response surface but find the optimal solution.
To solve this problem, the algorithm selects the next
sampling point that maximizes a value of the acqui-
sition function. There are two major algorithms in
kriging surrogate methods: the P-algorithm and ef-
ficient global optimization (EGO) (Kushner, 1964;
Jones et al., 1998).
Several heuristics that trade off exploration and
exploitation in GP optimization have been proposed
such as most probable improvement (MPI) and ex-
192
Takimoto N. and Morita H..
Global Optimization with Gaussian Regression Under the Finite Number of Evaluation.
DOI: 10.5220/0005559701920198
In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),
pages 192-198
ISBN: 978-989-758-120-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

pected improvement (EI) (Mockus, 1994; Mockus
et al., 1978). All these algorithms operate by balanc-
ing the local and global searching, and they are suit-
able for black-box optimization problems where only
a small number of function evaluations are possible.
Real-world optimization problems must be solved
at reasonable cost within feasible timeframes, which
strictly limits the number of evaluation. Unlike classi-
cal algorithms, which are unconcerned with the num-
ber of iterations, Bayesian optimization methods aim
to reduce the number of evaluations for searching
global optima.
For instance, Dexuan limited the number of evalu-
ations in a Particle Swarm Optimization (PSO)-based
algorithm. The IPSO algorithm is a variant of the
PSO algorithm that employs the global best position
to execute a global searching strategy (Zoua et al.,
2014). Combining the global searching strategy and
a mutation operation, it changes the balance between
global and local searching by its number of iterations.
Specifically, global and local searching is initiated
when the number of iterations is small and large, re-
spectively.
Here, we propose an algorithm that tackles global
optimization within a limited number of evaluations.
The crucial balance between global and local search
is achieved by improving the regression in the first
half of the iterations and improving the current best
solution in the second half. Within few evaluations,
the global optimum is searched by several acquisition
functions. Here, we adopt the PI and EI methods. The
effectiveness of using several acquisition functions is
experimentally confirmed.
The rest of this paper is organized as follows. Sec-
tion 2 reviews Bayesian optimization and popular ac-
quisition functions. In Section 3, we propose a simple
extension of the Bayesian optimizer using two acqui-
sition functions and present experimental results of a
standard test function taken from the global optimiza-
tion literature. The results confirm the effectiveness
of using two acquisition functions. Conclusions are
presented in Section 4.
2 BAYESIAN OPTIMIZATION
The objectivein global optimization problems is com-
monly a black-box function. That is, the objec-
tive function is not an analyzable expression, and its
derivatives are unknown.
Evaluation of the function is restricted to querying
at a point x and retrieving a response. Bayesian op-
timization with GP is a powerful strategy for finding
the optima of black-box functions.
In general terms, unconstrained Bayesian global
optimization proceeds as follows
1. Select initial points spread throughout the entire
input space. Run the computer code at these
points.
2. Using all previous function evaluations, fit a sta-
tistical model for the objective function.
3. Based on the fitted model, select the search points
in the input space for the next run.
4. Compute a stopping criterion. If this criterion is
met, stop the algorithm.
5. Run the computer code at the selected point in the
input space. Return to step 2.
In our method, the next point is decided from the pre-
vious datasets by Gaussian process regression, also
known as the kriging method. This method estimates
the mean and standard error of each point in the input
space from the datasets.
2.1 Gaussian Processes
After an initial experimental design or at some later
iteration of the algorithm, we have obtained the re-
sponses y(x)to n vectors x
1
,...,x
n
. Each x is a
d-dimensional vector of inputs x
1
,...,x
d
. The corre-
sponding output values for a given response variable
are denoted by Y = (Y
1
,...,Y
n
)
T
.
Following the approach of Santner, the response
is treated as a random function or a realization of a
Gaussian stochastic process (Santner et al., 2003).
The regression model is expressed as
Y
i
≡ Y(x
i
) = f(x
i
)β + Z(x) (1)
where f (x
i
) = ( f
1
(),... , f
p
()) are known regres-
sion functions, β = (β
1
,...,β
p
)
T
is a vector of un-
known regression coefficients, and Z() is a station-
ary Gaussian process on E[Z(x)] = 0. We also define
Cov[Z(x),Z(x
′
)] = σ
2
R(x,x
′
) for two input vectors
x and x
′
.
We now use the constant model of Martin and
Simpson, called ordinary kriging (Martin and Simp-
son, 2003). The global trend can be reduced to a sim-
ple constant-term model (i.e., f(x) = β) without sig-
nificant loss of model fidelity. The difference among
the constant, linear and quadratic models is negligi-
ble in the region around the data (Sasena, 2002). The
regression model thus reduces to
Y
i
≡ Y(x
i
) = β+ Z(x) (2)
The joint distribution of the predictor Y
0
= Y(x
0
) and
training data Y
n
= (Y(x
1
),...,Y(x
n
))
T
is the multi-
variate normal distribution
Y
0
Y
n
∼ N
1+n
β,σ
2
z
1 r
0
(x
0
)
T
r
0
(x
0
) R
(3)
GlobalOptimizationwithGaussianRegressionUndertheFiniteNumberofEvaluation
193

−0.4 −0.2 0.0 0.2 0.4
−2 −1 0 1 2 3 4 5
x
y
●
●
●
●
●
Figure 1: True curve y(x) = exp(−1.4x) × cos(3.5πx) (dotted line). The dots describe the five-point input design, and solid
red and dashed blue lines are the BLUP
ˆ
Y(x
0
) and the MSE σ
0|n
, respectively.
where 1 is a vector of ones. Suppose we have train-
ing data Y
n
= (Y
1
,...,Y
n
)
T
and correspondingn input
vectors x
1
,...,x
n
, where each x is a d-dimensional
vector of inputs x
1
,...,x
d
.
In this paper, the covariance function is the
squared exponential kernel with a vector of automatic
relevance determination (ARD) hyper parameters θ:
R(x,x
′
) = exp
−(x − x
′
)
T
diag(θ)
−2
(x − x
′
)
(4)
where θ = (θ
1
,...,θ
d
) are non-negativenumbers that
rescale between x and x
′
and diag(θ) is a diagonal
matrix with entries θ along the diagonal and zeros
elsewhere. This is probably most widely used kernel.
The θ values are determined by maximum likeli-
hood estimation. The correlation function is crucial
for tuning the properties of the fitted predictor to the
data. In each coordinate direction, larger θ
i
indicates
greater activity or nonlinearity. This model leads to
the best linear unbiased predictor and its associated
mean squared error.
In this model, we can show that the best linear
unbiased predictor (BLUP) of Y(x
0
) is
ˆ
Y(x
0
) =
ˆ
Y
0
≡
ˆ
β+ r
T
(x
0
)R
−1
(y − 1
ˆ
β) (5)
where
ˆ
β = (1
T
R
−1
1)
−1
1
T
R
−1
Y
n
is the general-
ized least squares estimator of β. r
0
= (R(x
0
−
x
1
),...,R(x
0
− x
n
))
T
, and R = (R(x
i
− x
j
)) is the
n× n matrix of correlations.
The mean squared error (MSE) of this predictor is
given by
σ
2
0|n
= σ
2
z
(
1−
1 r
0
0 1
T
1 R
−1
1
r
0
)
(6)
In this stochastic model, the MSE is zero at each of
the training data sites x
i
.
An example of this method is given in Figure 1.
Gaussian process regression returns the mean and
variance of a normal distribution over the possible
values of Y at point x. Stochastic processes are some-
times called “random function,” by analogy to ran-
dom variables.
3 MIXED ACQUISITION
FUNCTION
We are interested in situations with a limited number
of evaluations. Under these conditions, we control
the balance between exploitation and exploration to
improve the current best solution.
3.1 Acquisition Functions
One challenge of global optimization is balancing the
local and global searching. For fast global conver-
gence, Bayesian optimization algorithms must bal-
ance the search effort between the current local neigh-
borhood and the unknown areas, a problem known as
the exploitation and exploration trade off.
As mentioned above, exploitation searches around
the current best solution. Because better solutions of-
ten exist near the currently sampled best solution, ex-
ploitative searching carries a high chance of finding
these solutions.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
194

Exploration, on the other hand, searches over
the entire feasible region, especially insufficiently
searched areas. Exploration may identify high-quality
regions that have not been previously searched, pre-
venting wasteful searching of suboptimal regions.
Therefore, the exploitation and exploration tradeoff
is critical in designing globally convergent random
search algorithms.
Two of the most popular methods for balancing
exploration and exploitation are the P-algorithm and
EGO. Both algorithms fit the surface by standard krig-
ing techniques. To solve the often difficult global op-
timization problem and find the next solution for sim-
ulation, the P-algorithm and EGO maximize the prob-
ability of being delta-better than the current best solu-
tion and the expected improvement from the current
best solution, respectively.
The P-algorithm of (Kushner, 1964), originally
designed for one-dimensional problems, uses the
probability of improvement (PI) as the acquisition
function. The PI is the probability of improving the
current best solution at point x. The closed functional
form of PI is given by
PI(x) =Pr(Y
min
−Y
0
(x) > 0)
=Φ
µ(x) −Y
min
σ(x)
(7)
where Y
min
is the current best solution and Φ() is the
normal distribution function. µ(x) and σ(x) are the
predictor and its MSE, respectively, at point x.
More recently, the potential magnitude of the im-
provement at a point has been considered. Mockus
proposed the following criterion for maximizing the
expected improvement with respect to the current best
solution (Mockus et al., 1978):
I(x) = max(Y
min
−Y(x), 0) (8)
where Y
min
is the current best solution, Y(x) is the
BLUP at point x, and I(x) is the improvement of the
current best solution at point x.
The expected improvementis determined from the
expected value. Since Y(x) is a normal distribution
(
ˆ
Y,s
2
), we can get the EI in closed form as
EI(x) =E(I(x))
=(µ(x) − min(Y
n
)) Φ
µ(x) − min(Y
n
)
σ(x)
+ σ(x) φ
µ(x) − min(Y
n
)
σ(x)
(9)
where Φ() is a normal distribution function and φ()
is a normal probability density function. Y
n
is the
vector of outputs, and σ(x) is the standard error at
point x. µ(x) is the mean of the regression function
at point x. EI(x) computes the expected value of im-
proving the current best solution at point x.
Figure 2 presents 1d examples of Gaussian pro-
cess regression as well as the PI and EI acquisition
functions. The PI and EI values are high at the point x
with low
ˆ
Y or high σ value. The PI is especially high
around the current best solution, whereas EI weights
the uncertainty much more heavily than the PI.
3.2 Proposed Scheme
The acquisition functions PI and EI were discussed by
Brochu (Brochu et al., 2010). Each acquisition func-
tion acquires a different point to be sampled next.
Recall that our study focuses on situations with a
limited number of evaluations. The IPSO fully ex-
plores and exploits the solution space based on the
number of iterations (Zoua et al., 2014). This ap-
proach purportedly improves the quality of the par-
ticles in a swarm.
To ascertain the plausibility of this idea, we con-
duct experiments on a simple model based on PI and
EI. The proposed algorithm divides the number of
evaluations into two halves. In the first half of the it-
erations, the EI is adopted as the acquisition function
for global searching. The second half of the iterations
uses the PI for local searching.
In contrast to EI, which searches over a wide
range, PI is a greedy algorithm that tends to search lo-
cally. By balancing the global and local searching, we
can improve the effectiveness of Bayesian optimiza-
tion. For example, suppose that the objective func-
tion is to be evaluated 40 times. During the first 20
iterations, the algorithm globally evaluates the objec-
tive function by EI; during the second 20 iterations,
it locally evaluates the objective function by PI. The
procedure of the proposed method is shown in Algo-
rithm 1.
Algorithm 1: Mixed acquisition algorithm.
1: Choose an initial sampling
2: Compute
3: for t = 1,2, . . . , m do
4: Fit the kriging model on the known data
points.
5: if t < threshold then
6: Find x
t
= argmax
x
EI(x)
7: else
8: Find x
t
= argmax
x
PI(x)
9: end if
10: Augment the data D
1:t
= D
1:t−1
,(x
t
, y
t
) and
update the GP.
11: end for
GlobalOptimizationwithGaussianRegressionUndertheFiniteNumberofEvaluation
195

−0.4 −0.2 0.0 0.2 0.4
−2 −1 0 1 2 3 4 5
x
y
●
●
●
●
●
(a) Gaussian process regression.
−0.4 −0.2 0.0 0.2 0.4
0.00 0.05 0.10 0.15
x
EI
(b) Probability of improvement.
−0.4 −0.2 0.0 0.2 0.4
0.0 0.2 0.4 0.6 0.8
x
PI
(c) Expected improvement.
Figure 2: Gaussian Process posterior (top), and its acquisition functions: probability of improvement (center) and expected
improvement (bottom).
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
196
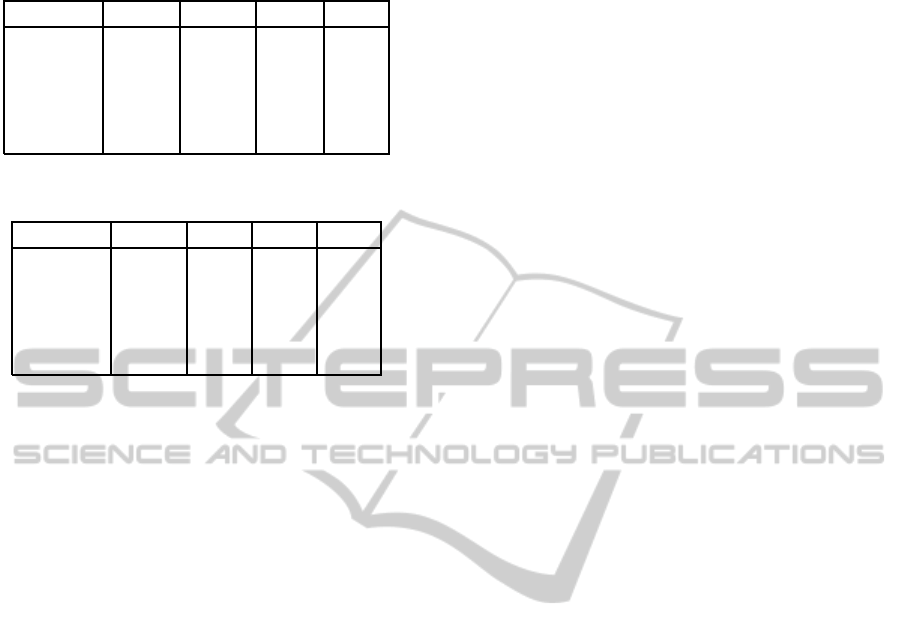
Table 1: Estimation results after 24 evaluations of a convex
function.
Iterations 6 12 18 24
EGO 36.40 23.42 13.65 6.74
3:1 36.40 23.42 13.65 5.36
1:1 36.40 23.42 11.90 5.48
1:3 36.40 20.79 12.87 5.01
MPI 36.72 20.84 6.44 4.13
Table 2: Estimation results after 48 iterations of a convex
function.
Iterations 12 24 36 48
EGO 23.42 6.74 3.33 1.33
3:1 23.42 6.74 3.33 1.39
1:1 23.42 6.74 3.49 2.28
1:3 23.42 5.48 2.53 1.32
MPI 20.84 4.13 3.34 2.38
3.3 Experimental Results
The performance of our algorithm was tested on the
convex function α
∑
5
i=1
x
2
i
, where α = 1/2. This five
dimensional function is continuous, bounded, and
convex. Each dimension of the input space is bounded
by [−10, 10].
The function was optimized 25 times and the
mean and variance of the current best solution was
computed at four time points (after 6, 12, 18, 24 itera-
tions, or after 12, 18, 36, and 48 iterations). Given an
initial random design of eight points, twenty or fifty
additional points were iteratively selected and eval-
uated by the MPI, EGO, and mixed acquisition algo-
rithms. To maximize the log marginal likelihoods, the
hyperparameters adopted in these experiments were
selected online.
We tested five models with different EI to PI ratios
(1:0, 3:1, 1:1, 1:3, and 0:1). The first and last of these
models are equivalent to EGO, and the P-algorithm,
respectively, while the ratios of 3:1, 1:1, and 1:3 are
denoted as 3:1, 1:1, and 1:3 respectively. Specifically,
we compared the performances of the mixed and stan-
dard acquisition functions.
Table 1 shows the case of 24 evalutions, where the
ratio of 1:3 yields a better solution than MPI after 12
iterations, but MPI obtains the best solution after 18
iterations.
In the 48 evaluation case, Table 2 shows that the
P-algorithm performs well in the first half, while the
ratio of 1:3 yields the best solution among the other
algorithms.
The results suggest that the greediness of the P-
algorithm is beneficial for optimizing convex func-
tions within a small number of iterations. When
the current best solution approximates the local op-
timum, the P-algorithm yields the strongest improve-
ment. Conversely, when the number of iterations is
increased, the EGO method enables efficient search-
ing. Therefore, the acquisition functions should be
selected based on the number of iterations.
After 36 iterations, the performance of the ratio
of 1:3 is clearly superior to that of the other algo-
rithms. Changing the acquisition function to improve
the searching strategy yields better optimization re-
sults than Bayesian optimization algorithms using a
single acquisition function.
4 CONCLUSION
We demonstrated that to obtain the best global op-
timal by Gaussian regression, the ratio of EI to PI
should be adapted to the number of iterations. At
some ratios, the combined approach yields superior
results to single acquisition functions, at other ra-
tios, MPI and EGO yields superior results. The time
point of switching the acquisition functions is unde-
termined. We selected the ratio that improves the cur-
rent best solution for a given objectivefunction within
a limited number of evaluations.
The GP-Hedge algorithm selects acquisition func-
tions for searching the next point by a bandit ap-
proach (Hoffman et al., 2011). Optimizing the pro-
posed method under limited evaluation conditions is
left for future research.
REFERENCES
Brochu, E., Cora, V. M., and De Freitas, N. (2010). A tuto-
rial on bayesian optimization of expensive cost func-
tions, with application to active user modeling and
hierarchical reinforcement learning. arXiv preprint
arXiv:1012.2599.
Hoffman, M. D., Brochu, E., and de Freitas, N. (2011).
Portfolio allocation for Bayesian optimization. In
UAI, pages 327–336. Citeseer.
Jones, D. R., Schonlau, M., and Welch, W. J. (1998).
Efficient global optimization of expensive black-box
functions. J. of Global Optimization, 13(4):455–492.
Kushner, H. J. (1964). A new method of locating the max-
imum point of an arbitrary multipeak curve in the
presence of noise. Journal of Fluids Engineering,
86(1):97–106.
Martin, J. D. and Simpson, T. W. (2003). A study on the
use of kriging models to approximate deterministic
computer models. In ASME 2003 International De-
sign Engineering Technical Conferences and Comput-
ers and Information in Engineering Conference, pages
567–576. American Society of Mechanical Engineers.
GlobalOptimizationwithGaussianRegressionUndertheFiniteNumberofEvaluation
197

Mockus, J. (1994). Application of bayesian approach to
numerical methods of global and stochastic optimiza-
tion. Journal of Global Optimization, 4(4):347–365.
Mockus, J., Tiesis, V., and Zilinskas, A. (1978). The appli-
cation of bayesian methods for seeking the extremum.
Towards Global Optimization, 2(117-129):2.
Santner, T. J., Williams, B. J., and Notz, W. (2003). The de-
sign and analysis of computer experiments. Springer
Science & Business Media.
Sasena, M. J. (2002). Flexibility and efficiency enhance-
ments for constrained global design optimization with
kriging approximations. PhD thesis, General Motors.
Zoua, D., Wangb, X., and Duana, N. (2014). An improved
particle swarm optimization algorithm for chaotic
synchronization based on pid control. Journal of
Information & Computational Science, 11(9):3177–
3186.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
198
