Genetic Algorithm based X-Ray Diffraction Analysis for Chemical

Control of Aluminium Smelters Baths

Shakhnaz Akhmedova

, Igor Yakimov

, Aleksandr Zaloga

, Sergey Burakov

, Eugene Semenkin

Petr Dubinin

, Oksana Piksina

and Eugene Andryushenko

Siberian State Aerospace University, Krasnoyarsk, Russia

Siberian Federal University, Krasnoyarsk, Russia

Keywords: Aluminium Industry, Aluminium Electrolyte, Cryolite Ratio, Bath Ratio, X-Ray Diffraction Analysis,

Rietveld Method, Genetic Algorithms, Chemical Control.

Abstract: Aluminium production is based on the high-temperature electrolysis of alumina in molten fluoride salts. Part

of the fluoride compounds continuously evaporates, which violates the optimal composition of the

electrolyte in the electrolytic baths. It causes a technological necessity for regular adjustment of the

electrolyte composition by the addition of fluorides according to results of automatic express analysis of the

electrolyte. Control of the main composition characteristics is performed automatically by XRD phase

analysis of crystallized electrolyte samples. The XRD method, usually used on aluminium smelters, requires

periodic calibration with reference samples, whose phase composition is exactly known. The preparation of

such samples is a rather complicated problem because samples include 5-6 different phases with variable

microcrystalline structure. An alternative diffraction method is the Rietveld method, which does not require

reference samples to be used. The method is based on the modelling of the experimental powder patterns of

electrolyte samples as the sum of the phase of component powder patterns, calculated from their atomic

crystal structure. The simulation includes a refinement of the profile parameters and crystal structure of

phases by the nonlinear least squares method (LSM). The problem with the automation of this approach is

the need to install a set of initial values of the parameters that can and should be automatically refined by

LSM to exact values. To solve this problem, the article proposed an optimization method based on an

evolutionary choice of initial values of profile and structural parameters using a genetic algorithm. The

criterion of the evolution is the minimization of the profile R-factor, which represents the weighted

discrepancy between the experimental and model powder patterns of the electrolyte sample. It is shown that

this approach provides the necessary accuracy and complete automation of the electrolyte composition

control.

1 INTRODUCTION

Aluminium production is based on the electrolysis of

alumina consisting of various forms of Al

Electrolytes of aluminium electrolysis baths in their

composition comprise melts of the senary system

Na-Al-Ca-Mg-F-O at a temperature of 930- 950

С.

Part of the components continuously evaporates

from the baths, which shifts the composition of the

electrolyte from the optimum point. It causes a

technological need for the regular adjustment of the

electrolyte composition by fluoride salts. The

amount of fluoride salt for addition into the

electrolysis bath is calculated from the results of

operational analysis of the chemical composition of

crystallized electrolyte samples.

The bath chemistry composition or more exactly

the bath ratio (BR is wt. NaF/AlF

) or cryolite ratio

(CR is mol. NaF/AlF

, CR=2BR) is a principal and

fundamental cell parameter to achieve the best

performance of electrolytic baths. The cryolite ratio

has a direct impact on the temperature control,

alumina solubility, ledge formation and current

efficiency of baths. The industrial characterization of

the bath electrolyte for process control is generally

carried out using two automatic calibrating methods:

a combined X-ray diffraction (XRD) analysis of CR

Akhmedova S., Yakimov I., Zaloga A., Burakov S., Semenkin E., Dubinin P., Piksina O. and Andryushenko E..

Genetic Algorithm based X-Ray Diffraction Analysis for Chemical Control of Aluminium Smelters Baths.

DOI: 10.5220/0005561900320039

In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 32-39

ISBN: 978-989-758-122-9

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

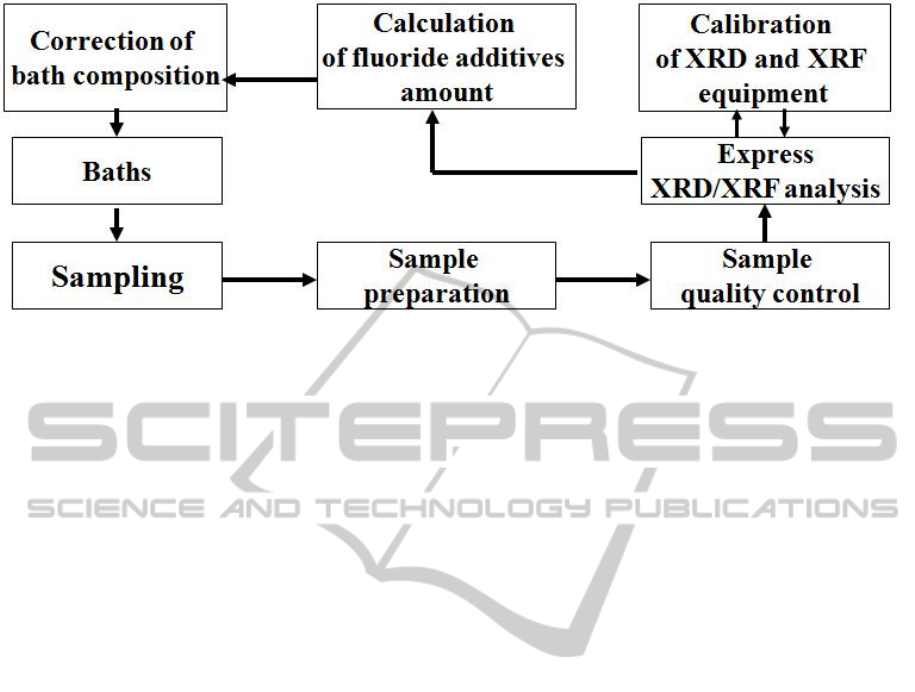
Figure 1: Scheme of the system of X-ray process control.

and X-ray fluorescence (XRF) analysis of CaF

and

MgF

. The technologically required accuracy of the

CR analysis is characterized by standard deviation in

0.02 CR units. The XRD method performs

quantitative phase analysis (QPA) of the mineral

composition of the electrolyte samples, and then the

CR is calculated from the found mineral phase

concentrations. Appropriate electrolyte reference

samples are required in the XRD and XRF

instrument calibration on crystalline phases and on

calcium and magnesium, respectively.

Figure 1 shows a scheme of the system of X-ray

process control and correction of electrolyte

composition, acting on the aluminium smelters.

Sampling from the cells is performed manually

by certain regulations. The preparation of samples

for analysis (grinding and fitting of powder in the

cell) is performed automatically, along the sample

preparation lines. Pressing quality control is carried

out visually, and X-ray phase analysis on an

automatic diffractometer. As a result of analysis the

mass of fluoride compounds to be added in the bath

to adjust the composition of the electrolyte to the

optimum is calculated. Reproducibility and accuracy

of analysis is periodically randomly checked on

routine and reference samples, respectively. In a

case of unsatisfactory results, the identification of

causes and, if necessary, re-calibration of the X-ray

equipment is carried out.

An alternative standardless XRD method is

quantitative phase full-profile analysis by the

Rietveld method (Young, 1993). The estimation of

the CR from XRD data by the Rietveld method is

possible with the technologically desired accuracy.

In addition, the Rietveld method universally applies

to baths from various plants that are sampled with

different methods and that are characterized by

different crystallinity and very diverse chemical

compositions. However, the Rietveld method is

interactive and time-consuming, and the industrial

electrolyte samples analysis from many hundreds of

baths should be fully automatic. Even the best

attempts to automate the full-profile CR analysis by

the Rietveld method has not yet provided

satisfactory accuracy (Feret, 2008). This is due to

the need for automatic refinement not only of the

profile parameters of X-ray diffraction patterns, but

also of the crystal structure parameters of some

fluoride electrolyte phases, which can vary in

different samples and critically affect the accuracy

of the CR determination.

An automatic method for XRD CR electrolyte

analysis is proposed in this article. The method is

based on an evolutionary hybrid genetic algorithm,

which controls the full-profile analysis by the

Rietveld method.

2 THE METHOD OF

EVOLUTIONARY

FULL-PROFILE

PHASE ANALYSIS

Evolutionary genetic algorithms simulate the

biological processes of natural selection in wildlife

and are successfully used in various fields of science

and technology (Paszkowicz, 2013). Genetic

algorithms are also used in diffraction structural

analysis (Feng, 2007; Kenneth, 2009) to determine

the approximate models of the atomic crystal

structure of materials by their X-ray powder

diffraction patterns. Crystal Structure includes the

coordinates of atoms in the symmetrically

independent part of the unit cell of crystal material

and some additional parameters. This information is

GeneticAlgorithmbasedX-RayDiffractionAnalysisforChemicalControlofAluminiumSmeltersBaths

accumulated in the Crystal Structure Databases

(ICSD, CSD).

The essence of the approach is to generate a

random set (population) of trial crystal structures

and evolve it using probabilistic formal genetic

operations: selection, crossover, mutation, etc.

Evolutionary selection is based on the offspring

structure evaluation by fitness function, which

represents here the weighted difference between the

model profile (calculated from the trial structure)

and the experimental diffraction pattern, i.e. one

must minimize the profile R

-factor of the Rietveld

method. The crystal structure model found is refined

by the Rietveld method based on the nonlinear least

squares. The Rietveld method is also used for the

quantitative X-ray analysis of multiphase materials.

The possibility of refinement of the actual crystal

structure of multiphase material phases makes QPA

"structurally sensitive" and thereby greatly increases

its accuracy.

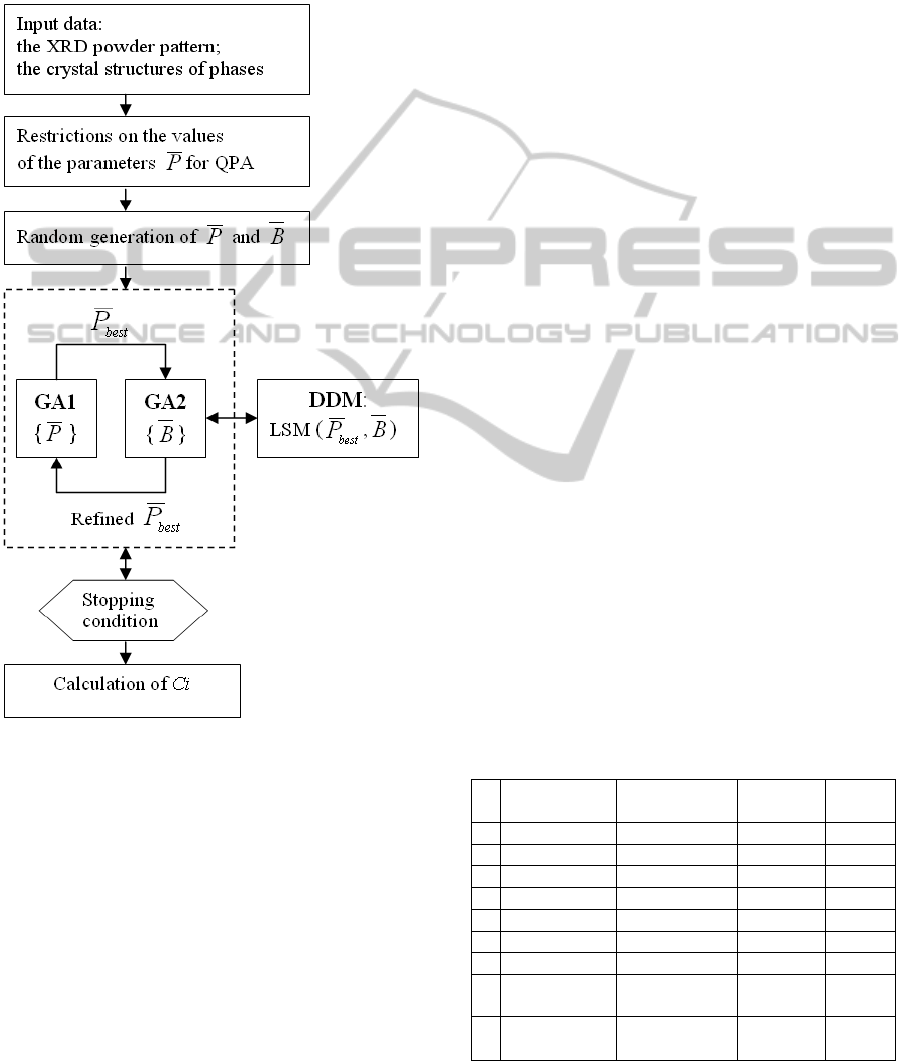
A two-level hybrid genetic algorithm (GA) of

structural analysis (Yakimov, 2009) is used mainly

to analyse the crystal structure of inorganic

substances. This GA performs the evolution of

profile and structural parameters of the Rietveld

method and controls its refinement by the derivative

difference minimizing method (DDM) (Solovyov,

2008) (an analogue of the Rietveld method).

The DDM method is based on the minimization

of difference curve derivatives:

()

min

→













−

∂













−

∂



YcYow

YcYowMF

(1)

where Y

and Y

are observed and calculated profile

intensities, correspondingly,

is the diffraction

angle, w is the weight coefficient and the summation

is fulfilled over the entire XRD powder profile.

The calculated profile is

,),,()(),(



Ω⋅=

jhprofistrihij

PPISKPYc

(2)

where К is constant; S

are scale factors of the

calculated diffraction profile for phase i; I

is the

integral intensity of diffraction reflexes h for phase i,

and I

is a function of the crystal structure

parameters for the phase i; Ω

is the profile function

of diffraction reflexes;

),(

strprof

PPP =

is the vector

of the profile and crystal structure parameters.

The DDM method includes a refinement of the

profile and crystal structure parameters

of phases

by the nonlinear least squares method (LSM). The

initial values of the parameters are determined by

the hybrid GA.

The GA fitness function is the R-factor of the

DDM, which represents a numerical derivative of

the relative difference between the calculated and

experimental powder pattern and is computed in a

similar way to the usual Rwp-factor of the Rietveld

method.

The authors of (Yakimov, 2012) have shown that

it is possible to perform the automated standardless

full-profile quantitative X-ray analysis on the basis

of a two-level hybrid GA with the DDM.

The concept of evolutionary XRD QPA is the

searching on the 1st level of the GA for the initial

approximation of a profile and refinable structural

parameters within given value ranges and then its

refinement by the DDM on the 2nd level of the GA.

The QPA feature is that the crude initial values of

the parameters can be determined in advance. For

example, the atomic coordinates of the crystal

structures are taken from the Crystal Structure

Databases. Therefore, the search for more accurate

initial values by the GA can be performed within

narrow ranges of parameter values. The flowchart of

the GA is shown in Figure 2.

The profile parameters include the width of the

diffraction reflexes, their shape, etc. Refinable

structural parameters include the coordinates of

atoms in the common positions of phase crystal

lattices. Together with them, the dimensions of

crystalline cell axes and texture parameters

(preferred orientation of particles) are refined, as

well as the scale factors S

of calculated diffraction

profiles of phases in the powder patterns of the

material. The listed parameters are binarized and

encapsulated in a string, the GA chromosome.

Objects of the evolution in GA2 are bit strings

Each bit set in ‘1’ specifies a corresponding

parameter of

to be refined by the DDM on the

current generation. The better the refining has been,

the higher B-type fitness is assigned. Thus genetic

operations over B-individuals generate strategies of

P-individuals refinement.

The evolution of the parameters in the iterative

execution process on both GA levels provides a

selection of good initial approximations for the

DDM. Periodic refinement of the best parametric

strings by DDM leads to a convergence of any of

them to low R

-factor values (less than 10%).

Then, the optimized scaling factors S

of the

calculated diffraction profiles of phases are used to

calculate the phase concentrations С

in the material:

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics



jjjjjjjjj

VMZSVMZSC

(3)

where V

, Z

are, respectively, the cell volume,

the number of formula units per cell and the

molecular weight of phase j; N is the number of

crystalline phases in the samples.

Figure 2: The flowchart of the two-level hybrid GA.

The XRD QPA procedure by the GA can be

divided into three stages.

(a) Search and refinement of profile parameters,

optionally together with the parameters of the

anisotropic broadening of lines caused by

microblocks and microstresses; decomposition of the

diffraction pattern and an initial refinement of

profile parameters are performed by the Le Bail

algorithm built into DDM.

(b) Search and refinement of structural

parameters together with texture parameters. Search

intervals of refinable atomic coordinates are given in

the neighbourhood of their positions in the

structures, taken from the database.

under the control of the 2nd level of the GA.

The precision of the method, estimated on high-

quality test data from the International Round Robin

on QPA CPD IUCr (Scarlett, 2002), was shown to

be 0.45 wt. % per phase.

3 ACCURACY EVALUATION

OF THE CR ANALYSIS AND

DISCUSSION

The method of the evolutionary full-profile QPA can

be configured for an automatic analysis of multiple

samples with the same type of phase composition as

a result of a selection of relevant search intervals and

settings of genetic operations. Industrial electrolytic

samples of aluminium production are suitable for

this purpose.

The phase composition of the electrolyte samples

is shown in Table 1, and the crystal structure of

these phases are taken from the database ICSD

(Inorganic Crystal Structure Database)

The high-quality industry reference samples

(IRS) of chemical and phase composition (Yakimov,

2008) prepared directly from the industrial

electrolyte samples of four large aluminium

smelters, containing calcium and magnesium, were

used for testing and accuracy evaluation of the

method.

The search intervals and settings of genetic

operations for the automatic analysis of the profile,

which were universal for this task, as well as the

structural parameters of fluoride phases have been

identified in special experiments of preliminary

studies.

Table 1: The phase composition of the electrolyte samples.

# Phases Chem. formula

Fraction

(% mass)

CR area

1. Cryolite Na

AlF

0~90 > 1.67

2. Chiolite Na

0~85 < 3.0

3. Fluorite CaF

0~9 > 2.45

4. Ca-cryolite 1 NaCaAlF

0~15 < 3.0

5. Ca-cryolite 2 Na

0~20 < 2.95

6. Weberite Na

MgAlF

0~15 < 2.85

7. Neiborite NaMgF

0~6 > 2.5

Sodium

fluoride

NaF 0~5 > 3.0

α-,

alumina

2~5

GeneticAlgorithmbasedX-RayDiffractionAnalysisforChemicalControlofAluminiumSmeltersBaths

CR values calculation from the found phase

concentrations were fulfilled according to the

formula:



⋅==

mol,AlF total

molNaF, total

(4)

where С

is the concentration of the i-th phase (%

mass), calculated according to (1); α

, β

are the

mass fractions of NaF and AlF

, respectively.

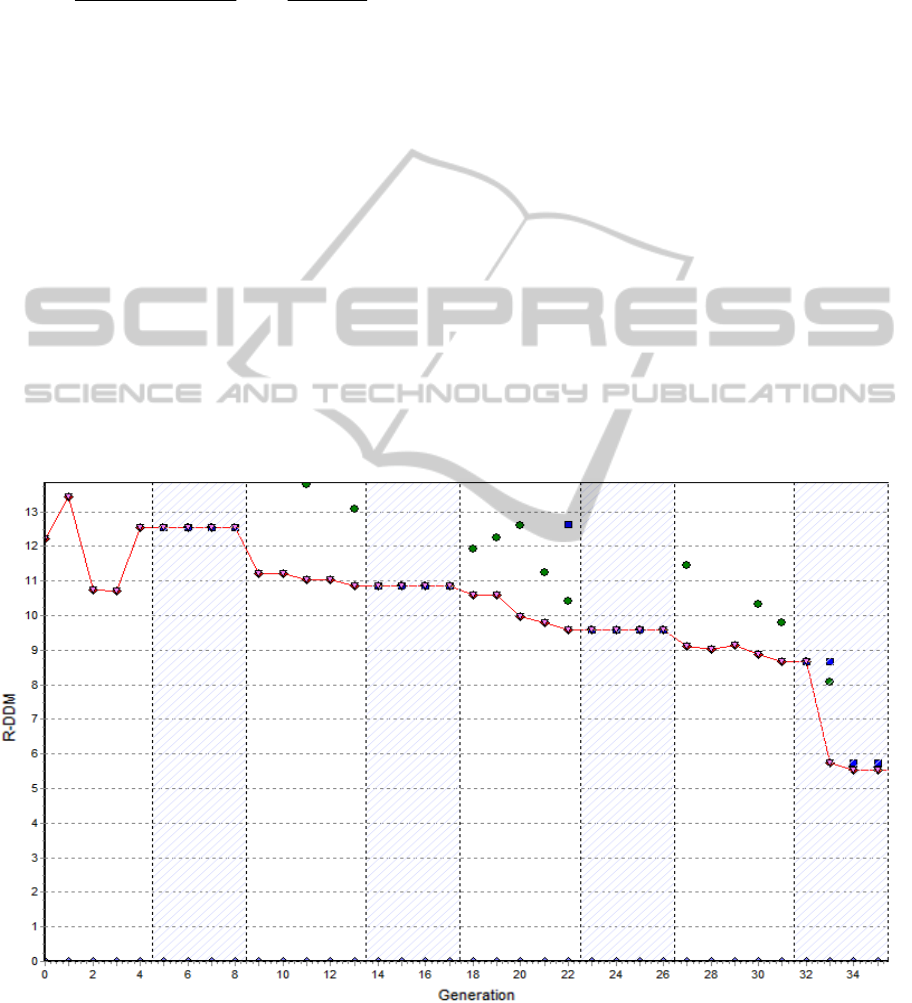
An analysis of 26 IRS was conducted. Figure 3

shows an example of a plot of the convergence in

the evolutionary full-profile QPA for one of them.

On the 1st level of the GA, the profile and some

structural parameter values are searched for in the

specified search range including atomic coordinates,

allowing variation in a given neighbourhood of its

positions in the structures of fluoride phases taken

from the structural data base ICSD, as well as

texture parameters of the phases. Level 2 of the GA

controls the gradual full-profile DDM-based

refinement of the best current solutions found on the

1st level of the GA. The sizes of test solution

populations were: 30 for the 1st level of the GA and

10 for the 2nd level of the GA. The alternation of

GA levels brings the iterative search process to the

true solution with R

= 5.6% after 37 generations of

evolution (in this example).

On the first three GA1 cycles, the best solution in

the population of the parametric strings gradually

improved and the R-factor decreased from 13.7% to

9.7%. However, a good approximation for the local

search has not yet been found and the refinement

with DDM cannot reduce the R

value (even-

numbered bands in Figure 3). Finally, on the 4th

GA1 cycle, the R-factor dropped less (from 9.7% to

8.8% in generations 27-31) and the approximation

was found which could be refined with the local

search. This approximation was refined with DDM

through the choosing of various parameter

combinations by the GA2 within the last 4

generations. After refinement, the R-factor

decreased from 8.8% to 5.6% and then was

stabilized.

After the final refinement of all parameters by

DDM, the R

was equal to 5.3% and the phase

concentrations calculated by (1) were used for the

CR calculation according to (2). The comparison of

the experimental and calculated final powder

patterns is shown in Figure 4.

Figure 3: The plot of convergence in the evolutionary XRD QPA from analysis of sample H803 from IRS; the x-axis

depicts the evolution generation number, the y-axis depicts the profile R

-factor; dotted vertical lines show the time of the

shift from the level 1 GA to the level 2 GA and back; the red line is the current best fitness value, blue dots show the current

worst fitness value, green dots show an average fitness value for the current population.

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

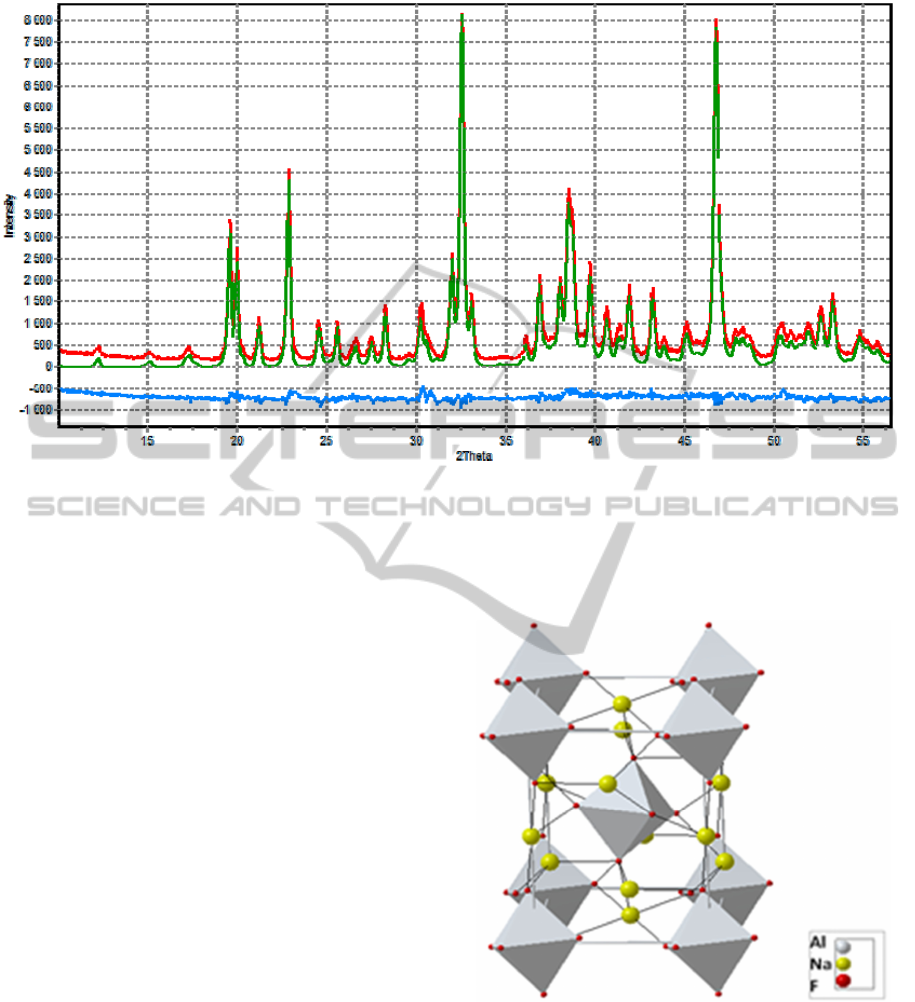
Figure 4: The experimental (red) and calculated (green) diffraction patterns for reference electrolyte sample Н803 and the

difference between them (blue, contains background from an amorphous phase of alumina); radiation with CuK

wavelength; R

-factor = 5.3%.

A feature of the method is the refinement of the

crystal structure of the electrolyte main phase. The

crystal structure of cryolite, chiolite and calcium

cryolite may vary slightly from sample to sample.

This is caused by the nonequilibrium crystallization

of sample dew, its sampling from the bath and

variable sampling factors such as the electrolyte

composition and temperature, mold mass and

temperature, weight of the sample, time since

loading the bath with alumina, etc. Figure 5 shows

the atomic crystal structure of cryolite and identifies

its main differences in two reference samples (C363

and C460).

The main structural variations are in the change

of the inclination angle and the geometric

dimensions of [AlF6]

-3

octahedras, and in the

corresponding shifts of Na atoms, located in the

common position for (Na2). This is reflected in the

variation of the lattice parameters, in particular, with

the c-axis size and the value of monoclinic angle β,

same as its intensity value. The difference in lattice

parameters leads to a perceptible shift of the

analytical diffraction reflexes of cryolite to about

2Θ ~ 0,02

- 0,03

, and the difference in the

coordinates of the atoms leads to a relative change in

the integrated intensity of the reflexes of up to 4%.

Neglect of these distortions of the crystal structure

significantly affects the accuracy of the electrolyte

analysis and the corresponding errors of the CR

determination are about 0.01-0.02.

Figure 5: Structure of cryolite and the main differences in

the samples C363 and C460, respectively:

- inclination angle of octahedras axis relative to the с-axis:

18.69

and 19.51

;

- edges and the angle of parallelogram in the base of the

octahedras: 2.484 Å, 2.727 Å, 88.50

and 2.513 Å, 2.569

Å, 89.04

;

- Na2 - Na1 distance: 3.249 Å and 3.188 Å.

GeneticAlgorithmbasedX-RayDiffractionAnalysisforChemicalControlofAluminiumSmeltersBaths

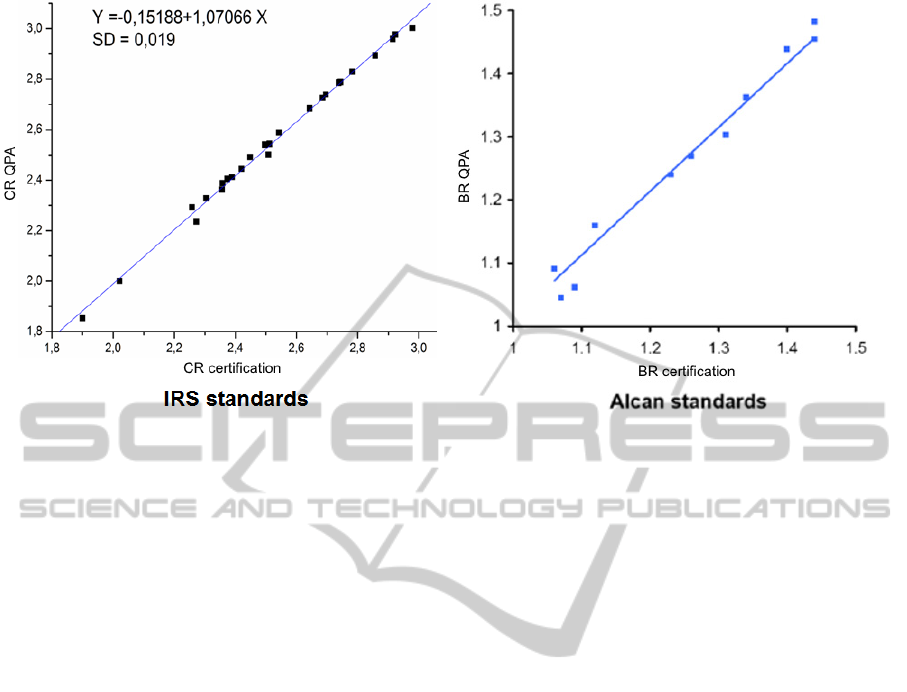
Figure 6: Regression charts for the estimation of the full-profile analysis accuracy:

(a) – for CR values, calculated by the data of evolutionary XRD QPA, to the certified CR values for electrolyte IRS

(b) – for BR values (BR = CR / 2), calculated by the automatic Rietveld analysis, to the certified BR values for electrolyte

reference samples (Alcan International Ltd, 2005).

The left side of Figure 6 shows the regression

graph of the corresponding calculated and certified

CR values for a set with 26 IRS of industrial

electrolyte. The calculated CR values correspond to

the certified CR values with precision, characterized

a standard deviation (SD) in 0,019 CR units. The

achieved accuracy completely satisfies the

technological requirements of the production.

The advantages of determining the CR by the

evolutionary XRD QPA method of relatively

automatic full-profile CR analysis by the Rietveld

method can be estimated by comparing the results

with the data of (Karsten Knorr, 2012). It should be

remembered that many of the aluminium factories,

instead of the cryolite ratio, apply its counterpart –

the bath ratio (BR), which is related as BR = CR/2.

The right side of Figure 5 shows the regression

graph of the corresponding BR values, calculated

according to the automatic full-profile BR analysis

by the Rietveld method, to the certified values for

the standard electrolyte samples of the company

ALCAN International Ltd (Alcan International Ltd,

2005), taken from (Karsten Knorr, 2012).

Unfortunately, the standard deviation value for the

BR graph in Figure 6 in (Karsten Knorr, 2012) was

not provided. To compare the graphs for BR and CR

on the same scale, all values along each of the axes

on the right graph should be doubled. After

performing this procedure it becomes apparent that

the standard deviation of the evolutionary XRD

QPA is at least twice as good.

4 CONCLUSIONS

The increased accuracy of the analysis by the

evolutionary QPA method can be explained through

the fact that the genetic algorithm searches various

variants of the approximate values of profile and

structural parameters (i.e. adapts them to a particular

sample) as well as periodically refining the best ones

on the 2nd level of the GA by the DDM – full-

profile analysis method. However, a variant of full-

profile analysis by the Rietveld method

automatically specifies the pre-selected initial values

(i.e. does not adapt to a particular sample) of the

profile and structural parameters.

The disadvantage of the current version of the

evolutionary QPA method is that the amount of

computational time is significantly higher than for

the existing calibration XRD methods of CR process

control. However, the development and optimization

of the evolutionary method certainly will increase

the processing speed of CR full-profile analysis and

bring it to a comfortable level.

Thus, this approach opens up new prospects for

electrolyte CR automatic standardless determination

by XRD data for chemical control on aluminium

smelting baths.

ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics

ACKNOWLEDGEMENTS

Research is fulfilled within state assignment of the

Ministry of Education and Science of the Russian

Federation for the Siberian Federal University

(project № 3098)

REFERENCES

Young, R.A., 1993. The Rietveld Method. Oxford

University Press, New York.

Feret, F.R., 2008. Breakthrough in Analysis of Electrolytic

Bath Using Rietveld-XRD Method. In: Light Metals.

pp. 343-346.

Karsten Knorr, 2012. Present progress in fast XRD

analysis applying the Rietveld method for bath

control. In: The 19th International Symposium and

Exhibition of ICSOBA.

Feng, Z.J., Dong, C., 2007. GEST: a program for structure

determination from powder diffraction data using a

genetic algorithm. In: J. Appl. Crystallogr. Vol. 40,

583 p.

Kenneth , D., Harris, M., 2009. Structure Solution from

Powder X-Ray Diffraction Data by Genetic Algorithm

Techniques, Applied to Organic Materials Generated

as Polycrystalline Products from Solid State Processes.

In: Materials and Manufacturing Processes. Vol. 24,

pp. 293–302.

Wojciech Paszkowicz, 2013. Genetic Algorithms, a

Nature-Inspired Tool: A Survey of Applications in

Materials Science and Related Fields: Part II. In:

Materials and Manufacturing Processes. Volume 28,

Issue 7 (Genetic Algorithms), pp. 708-725.

ICSD - Inorganic Crystal Structure Database. FIZ

Karlsruhe, http://www.fiz-karlsruhe.de/icsd.html.

CSD - Cambridge Structural Database. Cambridge

Crystallographic Data Centre, http://www.ccdc.cam.

ac.uk/products/csd/

Yakimov, Y.I., Semenkin, E.S., Yakimov, I.S., 2009.

Two-level genetic algorithm for a full profile fitting of

X-ray powder patterns. In: Z. Kristallogr. Suppl.30,

pp. 21-26.

Solovyov, L.A., 2008. The Derivative Difference

Minimization Method. Chapter 10. Powder Diffraction

Theory and Practice, ed. R.E. Dinnebier and S.J.L.

Billinge. In: Royal Society of Chemistry. 507 р.

Yakimov, I.S., Zaloga, A.N., Solov’ev, L.A., Yakimov,

Y.I., 2012. Method of Evolutionary

Structure_Sensitive Quantitative X-Ray Phase

Analysis of Multiphase Polycrystalline Materials. In:

Inorg. Materials. Vol.48, no.14, pp.1285–1290.

Nicola V.Y. Scarlett et al., 2002. Round Robin on

Quantitative phase analysis: samples 2. In: J. Appl.

Cryst. Vol. 35, pp. 383-400.

Yakimov, I.S., et al, 2008. Developing industry standard

samples of electrolyte aluminum electrolytic cells. In:

Standard samples. Vol. 4, pp.34-42.

Electrolytic Bath Standards, Alcan International Ltd.,

Quebec, Canada (2005).

GeneticAlgorithmbasedX-RayDiffractionAnalysisforChemicalControlofAluminiumSmeltersBaths