
Light Blind: Why Encrypt If You Can Share?
Pierpaolo Cincilla, Aymen Boudguiga, Makhlouf Hadji and Arnaud Kaiser
IRT SystemX, 8 avenue de la Vauve, 91120, Palaiseau, France
Keywords:
Cloud Computing, Data Confidentiality, Encryption.
Abstract:
The emergence of cloud computing makes the use of remote storage more and more common. Clouds provide
cheap and virtually unlimited storage capacity. Moreover, thanks to replication, clouds offer high availability
of stored data. The use of public clouds storage make data confidentiality more critical as the user has no
control on the physical storage device nor on the communication channel. The common solution is to ensure
data confidentiality by encryption. Encryption gives strong confidentiality guarantees but comes with a price.
The time needed to encrypt and decrypt data increases with respect to the size of input data, making encryption
expensive. Due to its overhead, encryption is not universally used and a non–negligible amount of data is
insecurely stored in the cloud. In this paper, we propose a new mechanism, called Light Blind, that allows
confidentiality of data stored in the cloud at a lower time overhead than classical cryptographic techniques.
The key idea of our work is to partition unencrypted data across multiple clouds in such a way that none of
them can reconstruct the original information. In this paper we describe this new approach and we propose a
partition algorithm with constant time complexity tailored for modern multi/many-core architectures.
1 INTRODUCTION
Nowadays, it becomes more and more common for
people and companies to store data outside their
premises. The successful pay as you go economic
model offered by public cloud providers is attracting
more and more customers thanks to its elasticity in
resource provision and to its availability guarantees.
However, storing data in a public cloud rises serious
security concerns. The loss of control of the physical
storage and computational devices, and the connected
nature of third-party hardware imply an expansion of
the attack surface.
Mechanisms to protect data confidentiality and in-
tegrity exist (Kamara and Lauter, 2010; Wang et al.,
2011) but nevertheless, the amount of plaintext data
stored in public clouds is non-negligible. Currently,
encryption is the main mechanism used to protect
data confidentiality. It offers strong guarantees but
its computational complexity prevents it from being
systematically used by cloud storage consumers. It
is time to provide to cloud consumers an alternative
system able to guarantee an acceptable level of con-
fidentiality at a much lower computational expense.
Such a technique benefits to users and companies that
actually do not secure their outsourced data.
In this paper, we propose an alternative to en-
cryption called Light Blind. Our idea is based on
the observation that splitting a file in chunks of non-
contiguous bits is faster than encrypting. The emer-
gence of multi-cloud systems (Bohli et al., 2013; Ste-
fanov and Shi, 2013) makes it possible to achieve con-
fidentiality by partitioning data chunks over multiple
providers. As such, each cloud provider can not ac-
cess the original data without colluding with all other
providers.
The remainder of this paper is organized as fol-
lows. Related work on multi–cloud storage and data
encryption is reported in Section 2. Section 3 de-
scribes the architecture, the partition algorithm and
the pattern hiding system. We discuss Light Blind
properties in Section 4. Conclusion and future work
are depicted in Section 5.
2 RELATED WORK
Srivastava et al. (Srivastava et al., 2012) proposed a
simple algorithm to better protect data by splitting
it into subfiles which are hosted in different virtual
machines within different cloud providers. The pa-
per dealt with operations to distribute and retrieve the
required subfiles (data) without encrypting them. The
proposed heuristic in (Srivastava et al., 2012) can host
361
Cincilla P., Boudguiga A., Hadji M. and Kaiser A..
Light Blind: Why Encrypt If You Can Share?.
DOI: 10.5220/0005562203610368
In Proceedings of the 12th International Conference on Security and Cryptography (SECRYPT-2015), pages 361-368
ISBN: 978-989-758-117-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

all of the data chunks within the same provider lead-
ing him to retrieve end-user’s data.
In (di Vimercati et al., 2014b), the authors propose
a combination of data distribution and swapping tech-
niques that protect both data and access confidential-
ity. In their solution data confidentiality is obtained
by ciphering the data, while access confidentiality is
obtained by changing the physical location of data at
every access. They make use of three independent
servers to further increase data access protection. In
our work we focus on providing data confidentiality
at a constant time complexity rather than providing
access confidentiality.
In (di Vimercati et al., 2014a), authors consider
the problem of protecting data confidentiality in the
cloud and point out two main techniques: encryp-
tion and fragmentation. An example of fragmenta-
tion technique is given in (Aggarwal et al., 2005).
They show how to provide confidentiality by parti-
tioning a database over two servers. As in fragmen-
tation techniques, we propose to partition data into
chunks which are stored in separate servers. Contrar-
ily to classical fragmentation, we make use of multi-
ple servers to achieve confidentiality at constant time
complexity without obfuscating data relations. We fo-
cus in an encryption-like mechanism at a lower com-
putational cost than classic cryptography.
For high availability and failure concerns when
storing data in the cloud, Qu and Xiong (Qu and
Xiong, 2012) proposed a distributed algorithm to
replicate data objects in different virtual nodes. Ac-
cording to the traffic load of all considered nodes, the
authors defined different actions: replicate, migrate,
or suicide to meet end-user requirements. The pro-
posed approach consists in checking the feasibility of
migrating a virtual node, performing suicide actions
or replicating a copy of a virtual node. However, the
stored data suffers from vendor lock-in as the totality
of data is stored within one provider.
In (Mansouri et al., 2013), authors dealt with the
problem of multi-cloud storage with a focus on avail-
ability and cost. The authors proposed a first algo-
rithm to minimize replication cost and maximize ex-
pected availability of objects. The second algorithm
has the same objective but is driven by budget con-
straints. However, the paper does not embed secu-
rity aspects apart from dividing the data into chunks
or objects. In (Sachdev and Bhansali, 2013), authors
proposed encrypting data locally using the Advanced
Encryption Standard (AES) algorithm before sending
the data for storage in the cloud.
In (Hadji, 2015), Hadji addresses encrypted data
storage in multi-cloud environments and proposes
mathematical models and algorithms to place and
replicate encrypted data chunks while ensuring high
availability of the data. To enhance data availabil-
ity, the author presents two cost-efficient algorithms
based on a complete description of a linear program-
ming approach of the multi-cloud storage problem
and then shows the scalability and cost-efficiency
of the proposed multi-cloud distributed storage solu-
tions. To guarantee data confidentiality, the author
uses data chunks encryption with AES, which im-
poses a potentially high overhead when uploading and
downloading the data.
We notice that most of the aforementioned works
refer to the use of symmetric cryptography and AES
particularly when providing data confidentiality. AES
is a special case of Rijndael algorithm (Daemen and
Rijmen, 1998) when considering 128 bits long in-
put blocks. AES supports the following key lengths
128, 192 and 256 bits, and consists of 10, 12 and 14
rounds, respectively. AES can be used in different
block cipher modes. The most known modes are the
following (Ferguson et al., 2011):
• Electronic Code Book mode (ECB): in ECB mode,
we encrypt each plaintext input block P
i
sepa-
rately such as: C
i
= AES
Encrypt(K,P
i
) where K
is the encryption key and C
i
is the corresponding
ciphertext. Note that ECB suffers from a pattern
recognition problem and its use in practice is dep-
recated.
• Cipher Block Chaining mode (CBC): in CBC
mode, we apply an exclusive OR (XOR) to ev-
ery plaintext input block with the previous cipher-
text block as following C
i
= AES Encrypt(K,P
i
⊕
C
i−1
). Note that the first ciphertext block C
0
is computed from the encryption of the first
plaintext block P
0
with the key K as C
0
=
AES Encrypt(K,P
0
⊕ IV) where IV is a random
initialization vector.
• Output Feedback mode (OFB): in OFB mode,
C
i
= K
i
⊕ P
i
where K
i
= AES Encrypt(K,K
i−1
)
and K
0
= IV . OFB and CBC modes are sequential
in that each block can not be treated until getting
some information from the previous block.
• Counter mode (CTR): in CTR mode, K
i
=
AES Encrypt(K,Nonce k i) and C
i
= K
i
⊕ P
i
.
In our work, we propose a new efficient and scal-
able solution capable of handling large data thanks to
its constant time complexity. We first split the data
into small chunks and then apply a new approach to
better dispatch them across available data centers and
providers. We propose a smart mechanism providing
each cloud host with only a random subset of data
chunks. Our algorithm provides patterns distribution,
without data encryption. It has constant time exe-
SECRYPT2015-InternationalConferenceonSecurityandCryptography
362

cution and guarantees data confidentiality. It can be
easily implemented over multi-cores architecture and
profits from multi-threading. In the following sec-
tion, we discuss in details our proposed solution and
how it can tackle secure data storage between differ-
ent multi-cloud providers.
Figure 1: System overview.
3 Light Blind ARCHITECTURE
We consider a system composed of a set of clients,
a broker, and a set of cloud storage providers (C =
{c
1
,c
2
,. ..c
n
}). The client uses the broker services to
securely store its data in the set of clouds storage. The
broker is in the client machine or in a cloud trusted by
the client (see Figure 1).
3.1 Protocol Overview
The clients send to the broker requests to
store/retrieve files in/from the cloud.
A store request contains a file and a set of con-
straints (e.g., the minimum/maximum number of
providers, the number of replicas or their geograph-
ical location, etc.). The broker call a Policy Service
that returns a set of destination clouds that respect,
if possible, all the constraints. Then the broker calls
a partition algorithm that splits the file into shares,
one for each cloud identified by the Policy Service.
We assume that the Policy Service returns at least two
clouds. Finally, it sends each share to the appropri-
ate cloud. The broker store locally all the information
needed to retrieve and reconstruct the original file.
A retrieve request contains the file identifier. The
broker fetch all the shares corresponding to that file
and reconstruct the original file that is returned to the
client.
The Policy Service mechanism is orthogonal to
the obfuscation system described in this paper and
well known in the literature (Mansouri et al., 2013;
Papaioannou et al., 2012). The details of such a mech-
anism are out of the scope of this work and not de-
scribed here.
3.2 Light Blind Partition Algorithm
To partition the input plaintext over a set of cloud
providers C = {c
1
,c
2
,. ..c
n
} we proceed as follows:
i) we divide the input in blocks of k bits each (except
the last block that can be smaller), ii) we generate a
key that map each bit of the block to a cloud provider
c
i
∈ C, iii) we generate for each cloud a share contain-
ing the bits that belong to it according to the key, and
iv) we assign each share to its cloud.
The key is generated by randomly taking for each
bit of the block a cloud provider c
i
∈ C. The dimen-
sion of the key is proportional to the dimension of the
block
1
. Figure 2 shows an example of Light Blind
partition algorithm.
The key property of this algorithm is that each step
is fully parallelizable and its execution time is con-
stant: does not depend on the plaintext size. That is,
each block can be treated in parallel by a different
thread with no need of synchronization.
3.3 The Patterns Problem
The partition algorithm does not hide well patterns of
the plaintext. Similarly to AES Electronic Code Book
(ECB) encryption mode, if the plaintext has a pattern,
the pattern will be reflected in the ciphertext. Each
block is encrypted using the same key, so for the same
blocks corresponds the same ciphertext. In order to
solve this problem, other block cipher modes (Sec-
tion 2) use a different encryption key for each block.
As such, patterns of the plaintext are not reflected in
the ciphertext .
Light Blind faces the patterns problem in an inno-
vative way by hiding patterns without trade on scal-
ability. We modify the algorithm described in Sec-
tion 3.2 as follow: after having generated the shares
(step iii) and before sending them to the clouds (step
iv), we perform a series of data transformations that
shuffle the block content and that cannot be undone
unless all the shares are available. That is, clouds col-
laborate between them to retrieve all the shares or the
1
There is a trade off to consider: in one hand to optimize
the amount of data stored in the broker we want to minimize
the size of the key (i.e., the smaller, the better), in the other
hand for the robustness of the encryption hold the rule “the
bigger the better” (see Section 3.7).
LightBlind:WhyEncryptIfYouCanShare?
363

An input data of 18 bits is partitioned in three clouds C1,C2 and C3 using blocks of 6 bits. (a) An array of the size of a block (6 in this
example) is generated. The array contains in each cell the identifier of one of the target clouds (C1,C2,C3) selected randomly. (b) - (c) The
input data is split in blocks of size 6. (d) Each block is paired with the key generated in step a. Each bit is moved in a share corresponding to
the cloud indicated by its pair in the key. (e) - (f) Each share generated in step d is moved to its associated cloud.
Figure 2: Light Blind Partition Algorithm Example.
Figure 3: Pattern Example.
attacker eavesdrop on the network. This extra step is
still fully parallelizable and its execution time is con-
stant.
3.4 The Cut-and-Shuffle Algorithm
Overview
As introduced in Section 3.4 the Light Blind partition
algorithm does not hide patterns. Figure 3 shows an
example of pattern in the input blocks which is re-
flected in the produced shares for a given key. In the
example the three shares show a different pattern that
repeats each 4 bits. To solve this problem we do not
send shares to clouds right after their generation (step
iii in Section 3.2) but we add an extra step that cut
data contained in the shares and then shuffle it. We
first cut rows of shares to form pattern-free columns,
then we shuffle those columns to form new shares.
If a share contains a pattern of n bits and we cut the
share in blocks of k bits with k < n and k prime with
n, the first n blocks of k bits each will not contain any
pattern present in the share (see Figure 4).
Cut Phase
In the cut phase we align shares in rows and then
we cut each row in blocks of k bits. The first block
of each row (i.e., share) forms the first column,
the second block of each row forms the second
column and so on (vertical red lines in Figure 4).
Notice that the first n columns produced in the cut
phase do not contain any pattern of the plaintext
thanks to the assumption that the cut length k is
prime with the plaintext pattern length n.
Shuffle Phase
In the shuffle phase we associate the first column
to the first cloud, the second column to the second
cloud, and so on. When there are no more clouds
we restart the association from the first cloud in
SECRYPT2015-InternationalConferenceonSecurityandCryptography
364
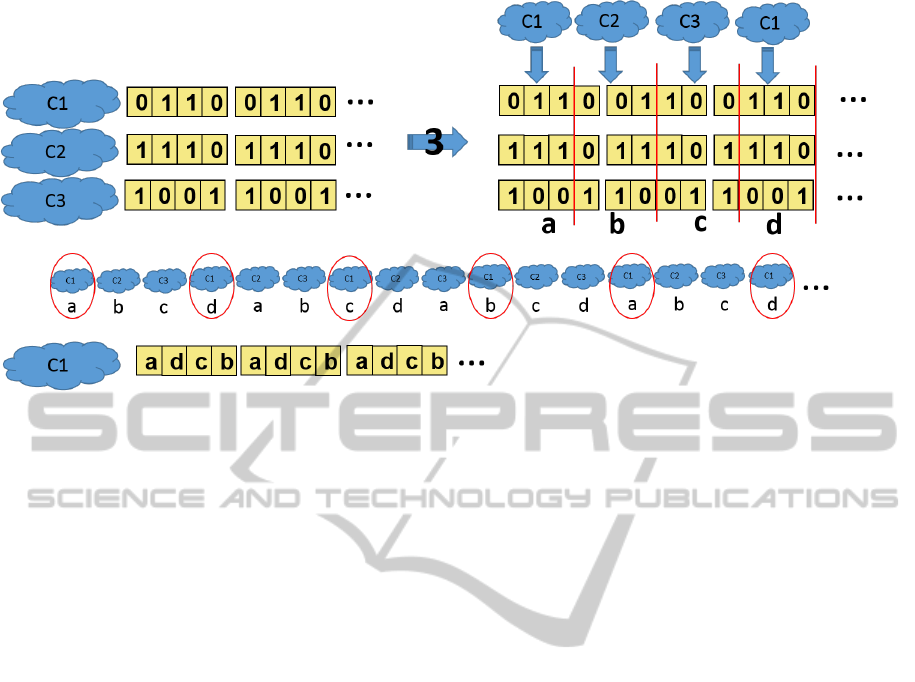
Figure 4: Cut-and-Shuffle Step Example.
a circular manner. This new association between
columns and clouds generate a new set of shares
that do not contain the pattern of the plaintext.
The problem of the Cut-and-Shuffle algorithm is
that new patterns appear: in the cut phase for a pattern
of length n, the first n columns are unique. After the
n
th
columns they repeat: the column n + 1 is equal to
the column 1, the column n + 2 is equal to the column
2, etc.
Consider the example in Figure 4. There are three
shares each one containing a pattern of length 4 (0110
for the cloud c
1
, 1110 for the cloud c
2
and 1001 for
the cloud c
3
). In the cut phase (vertical red lines in the
Figure 4) we cut the pattern of length n = 4 in blocks
of length k = 3 (notice that 3 is minor than 4 and prime
with it), the initial patterns (0110, 1110 and 1001) are
broken and none of the generated blocks of three bits
contains any pattern. We associate each column to a
new share in a circular manner. The figure shows the
first four columns, named “a”, “b”, “c” and “d”. Each
column contains 9 bits and is unique. The problem
comes after the fourth column: cutting a pattern of
length 4 in columns of length 3, imply that each four
columns the cut repeat, i.e., the column 5 will be equal
to the column 1, the column 6 equal to the column 2,
and so on. More in general what happen is that cut-
ting a pattern of length n in blocks of length k, the cut
will repeat each n ∗ k bits, that is each n blocks. This
implies that the column i will be the same as the col-
umn i mod n. In the bottom part of Figure 4 we have
named the four columns a, b, c and d and we show,
for the cloud c
1
, the new pattern that arises: a-d-c-b.
Since clouds are associated to columns in a circular
manner the cloud c
1
will receive the same columns a,
d, c and b in this order, repeatedly. This means that
cloud c
1
will observe a new pattern composed by the
concatenation of columns a-d-c-b. In the example of
Figure 4 the new pattern has a length of four columns
of 9 bits each. More in general using this technique
the new share will contain a pattern that repeats ev-
ery k∗ #of rows (clouds) ∗n. This is a key property of
the Cut-and-Shuffle algorithm: after a cut-and-shuffle
operation the algorithm mix together a number of bits,
breaking every pattern they can contain.
3.5 The Cut-and-Shuffle Algorithm
Iteration
The pattern problem can be mitigated by cutting rows
of shares in columns and assigning columns to a new
set of shares. The problems of this technique is that i)
it does not completely hide patterns but it only makes
them somehow bigger and ii) needs to know the pat-
tern length to find a number smaller than the pattern
length and prime with it. In practice, we solve those
problems by iterating our algorithm multiple times
using each time a different prime number. Figure 4
shows how patterns of 4 bits are mixed to form pat-
terns of 36 bits cutting the initial share in columns
of 3 bits. The idea is to iterate the same procedure
of Cut-and-Shuffle multiple times in order to increase
the size of bits mixed to a dimension that will hide all
possible patterns.
In our algorithm we repeat the cut and shuffle step
ten times. We use the sequence of the first 10 odd
prime numbers (3, 5, 7, 11, 13, 17, 19, 23, 29 and 31)
to choose the size of the block at each step. For seek
of simplicity, we first assume that the input does not
LightBlind:WhyEncryptIfYouCanShare?
365

contain patterns that are multiple of any of the prime
numbers used in the cut step to avoid breaking the as-
sumption that the length of the cut is prime with the
length of the pattern. Then we generalize our descrip-
tion considering those cases.
Figure 5 shows the Cut-and-Shuffle’s iterations.
We call size of a pattern or a column the number of
its bits. The first iteration makes a column each 3
bits, the second each 5 bits, then 7 bits, etc., until
the last iteration that cuts a column each 31 bits. The
Cut-and-Shuffle algorithm breaks patterns regardless
their size: the first iteration hides all possible patterns
with size not multiple of 3 in bigger patterns of size
(3 * #of rows * n) bits where n is the size of the pat-
tern. In the example of Figure 5 after the first itera-
tion the new shares have patterns of size 36. In the
second iteration all patterns (we assume they are not
multiple of 5) are hidden in bigger patterns of size
5 * #of rows (clouds) * n where n is the size of the
pattern generated in the previous iteration (36 in the
example). In the instance of Figure 5 after the sec-
ond iterations the new pattern size is 180 (= 36 ∗ 5)
bits. After each step of the Cut-and-Shuffle algorithm
the size of a potential pattern in the output share is
increased by a factor equals to the number used in
the cut phase. At the end of the 10
th
transformation
any pattern in the output share cannot be smaller than
the initial pattern multiplied by 1.0028 × 10
11
(that is
3∗ 5∗ 7∗ 11∗ 13∗17∗19∗23∗29∗31). This is equiv-
alent to mixing together blocks of 1.0028 × 10
11
bits,
making the algorithm hiding every pattern smaller
than this size. It can be seen as a classic ECB
with a block size (and consequently a key size) of
1.0028 × 10
11
bits.
As discussed in Section 3.4, if we cut a share con-
taining a pattern of size n in blocks of k bits, and
k is prime with n, the first n blocks of k bits are
unique (i.e., do not contain the pattern). More gen-
erally, by cutting a pattern of size n in blocks of size
k, the generated blocks repeat each n/k blocks if n
is divisible by k, or each n blocks otherwise. The
amount of unique blocks generated by the cuts is im-
portant because the more they are, the better patterns
are hided. Intuitively, a sequence of unique blocks of
size s mixes all potential patterns in the correspond-
ing s bits in the input. Since we do not know in ad-
vance the size of patterns that can be contained in the
plaintext, in Cut-and-Shuffle algorithm we have used
a sequence of prime numbers for the block size to
minimise the probability that the pattern size is di-
visible by the block size. Moreover, prime numbers
do not share any divisor, so a pattern can be divisi-
ble by (or multiple of) only one prime number. This
implies that in the worst case at most one of the ten
iterations of the Cut-and-Shuffle algorithm is not in-
cisive. The impact of having a pattern multiple of one
of the ten prime numbers is negligible because in the
worst case the algorithm mix together 3.2348 × 10
9
(3 ∗ 5 ∗ 7 ∗ 11 ∗ 13 ∗ 17 ∗ 19 ∗ 23 ∗ 29) bits instead of
1.0028×10
11
(3∗5∗7 ∗11∗13∗17 ∗19∗23 ∗29∗ 31)
bits. Mixing 3.2348×10
9
bits is far more than enough
to hide all possible patterns in the real (an may be also
in the imaginary) world.
For sake of simplicity, in the previous discussion
we have considered that patterns reflected from the
plaintext to the shares have the same size. This is not
necessarily the case. It is possible that a pattern in the
plaintext give different patterns of different length in
the shares. In this case the Cut-and-Shuffle is even
more efficient in hiding patterns because columns re-
peat with a lower frequency. Intuitively, in the cut
step of the Cut-and-Shuffle algorithm, if all rows (i.e.,
shares) have a pattern of the same size n, the pattern
repeats each n columns, while if a row has a pattern of
size n and another has a pattern of size n
0
, then the pat-
tern repeats each k columns, k being the least common
multiple of n and n
0
. We recall that the less columns
repeat the best Cut-and-Shuffle algorithm works.
3.6 Light Blind Decryption Mechanism
In order to retrieve files, the broker should first fetch
all the shares from the clouds. Then, it applies the in-
verse operation of the Cut-and-Shuffle and finally ap-
plies the encryption key to reconstitute the plaintext.
Notice that all these operations, same as for encryp-
tion, have a constant time complexity (i.e., the time
needed to reconstruct the input does not depend on
the input size).
To reverse the Cut-and-Shuffle algorithm, it is suf-
ficient to repeat all the cut and shuffle phases using
the prime numbers in the inverse order: from 31 to
3. The broker retrieves all the shares, puts them in
rows, and starts to cut columns of size 31. Then, it
shuffles the columns to form new shares (same as in
the encryption phase). Next, it repeats the cut phase
with columns of size 29. Once it has iterated all the
prime odd numbers, it has the original shares calcu-
lated at the first step of the Light Blind Partition Al-
gorithm. In order to reconstruct the original file, the
broker uses the encryption key to build the original
sequence of bits from the shares.
3.7 Security Analysis
Our system provides data confidentiality by spreading
the original input in several clouds.
An adversary needs to access all the shares of the
SECRYPT2015-InternationalConferenceonSecurityandCryptography
366

Figure 5: Cut-and-Shuffle Iterations.
original data to be able to undo the Cut-and-Shuffle
transformations. If she misses one of the shares there
is no way to undo Cut-and-Shuffle transformations
and the data is completely opaque: the adversary does
not know the original position of the bits it has nor the
position of the missing bits in the input. This gives to
the user the assurance that, unless the adversary can
access all the shares, data confidentiality is kept.
If an adversary can collect all the shares, for ex-
ample thanks to a collaboration between clouds or
eavesdropping in the network during the transmis-
sion, the Cut-and-Shuffle step can be easily undone
by the adversary and our system rollback to a classic
ECB scheme. The problem of ECB is that it does not
hide well patterns.
An interesting property of Light Blind is that the
use of a secret key to spread data in the clouds is only
needed to offer a minimal (ECB-like) protection if an
adversary collects all the shares. If we assume that
clouds do not collaborate, and that the communication
channel is somehow secure, then Light Blind does not
need to use any secret because an adversary cannot
undo the Cut-and-Shuffle phase. If we assume a pub-
lic channel then the user may be interested in ensur-
ing the confidentiality of the communications chan-
nel, for example by using HTTPS. The discussion of
the communication overhead is out of the scope of
this paper.
As discussed previously, if all shares are known
by an adversary, Light Blind rollbacks to ECB. The
difference between a classical ECB and Light Blind
is that in our system, the produced output (the shares)
is a partial order of the initial input: if a bit b is before
a bit b
0
in a share, then b is before b
0
also in the plain-
text. This translates by a decrease of the possible bits
permutations of the ciphertext to produce the plain-
text. If a block B of size B
s
is divided into n shares
S = (s
1
,s
2
,. ..,s
n
) then the possible permutations of
shares in the original block are
(s
1
+s
2
+...+s
n
)!
s
1
!s
2
!...s
n
!
where
(s
1
,s
2
,. ..,s
n
) represents the size (i.e., the number of
bits) of a block in each share. This is weaker than a
random key because in the case of a random key the
possible permutations are (s
1
+ s
2
+ .. . + s
n
)!.
4 DISCUSSION
The motivation of our work is to provide users with a
simple and efficient way to obtain data confidentiality
in the cloud at a constant computational time. Con-
stant computational time means that the time needed
to transform data to make it unintelligible does not
depend on the size of data.
This goal is achieved thanks to the fact that all
steps of our algorithm are parallelizable: we process
blocks of data and each block has i) the same dimen-
sion and ii) applies the same operations.
In the first phase, we encode each block with an
encryption key, similarly than in classical ECB in or-
der to obtain shares of the original data. This phase
can be executed in parallel in all the blocks, so its
time complexity is constant. In the second phase we
iteratively cut and shuffle shares in order to mix them.
Each iteration of the Cut-and-Shuffle algorithm can
be executed in parallel in all the columns without syn-
LightBlind:WhyEncryptIfYouCanShare?
367

chronization, so its time complexity is constant. Since
the number of iterations of the second phase is con-
stant as well (10), the time complexity of the second
phase is constant.
Of course the bigger is the input, the more are the
resources needed to parallelize Light Blind. Never-
theless, modern devices have more and more CPU,
and consequently they are able to execute more and
more work in parallel, so our algorithm makes a good
use of current architectures.
5 CONCLUSION
In this paper we show an innovative way to make
use of multi-cloud systems and block ciphering to ob-
tain data confidentiality at a constant time complexity.
Our system provides simultaneously ECB paralleliz-
ability and the ability to hide patterns. This is possible
thanks to the key idea of splitting data into multiple
shares that are stored in different clouds.
Light Blind positions between classic encryption
with ECB mode providing confidentiality at a con-
stant time complexity and the ability of hiding pat-
terns provided by other encryption modes such as
CBC and OFB.
Our system benefits to users who do not encrypt
their data stored in the cloud. The constant time com-
plexity of Light Blind makes suitable data to be pro-
tected in a more systematic way. No matter the size
of your data or how often you need it, the overhead
you have to pay to gain confidentiality is small and
predictable.
ACKNOWLEDGEMENTS
This research work has been carried out in the frame-
work of the Technological Research Institute Sys-
temX, and therefore granted with public funds within
the scope of the French Program Investissements
d’avenir.
REFERENCES
Aggarwal, G., Bawa, M., Ganesan, P., Garcia-Molina, H.,
Kenthapadi, K., Motwani, R., Srivastava, U., Thomas,
D., and Xu, Y. (2005). Two can keep a secret: A
distributed architecture for secure database services.
CIDR 2005.
Bohli, J.-M., Gruschka, N., Jensen, M., Iacono, L., and
Marnau, N. (2013). Security and privacy-enhancing
multicloud architectures. Dependable and Secure
Computing, IEEE Transactions on, 10(4):212–224.
Daemen, J. and Rijmen, V. (1998). Aes proposal: Rijndael.
di Vimercati, S. D. C., Erbacher, R. F., Foresti, S., Jajodia,
S., Livraga, G., and Samarati, P. (2014a). Encryption
and fragmentation for data confidentiality in the cloud.
In Foundations of Security Analysis and Design VII,
pages 212–243. Springer.
di Vimercati, S. D. C., Foresti, S., Paraboschi, S., Pelosi,
G., and Samarati, P. (2014b). Protecting access confi-
dentiality with data distribution and swapping.
Ferguson, N., Schneier, B., and Kohno, T. (2011). Cryptog-
raphy Engineering: Design Principles and Practical
Applications. Wiley.
Hadji, M. (2015). A mathematical programming approach
to multi-cloud storage. In Proceedings of the 5th In-
ternational Conference on Cloud Computing and Ser-
vices Science, CLOSER ’15.
Kamara, S. and Lauter, K. (2010). Cryptographic cloud
storage. In Sion, R., Curtmola, R., Dietrich, S., Ki-
ayias, A., Miret, J., Sako, K., and Seb, F., editors,
Financial Cryptography and Data Security, volume
6054 of Lecture Notes in Computer Science, pages
136–149. Springer Berlin Heidelberg.
Mansouri, Y., Toosi, A. N., and Buyya, R. (2013). Broker-
ing algorithms for optimizing the availability and cost
of cloud storage services. In Proceedings of the 2013
IEEE International Conference on Cloud Computing
Technology and Science - Volume 01, CLOUDCOM
’13, Washington, DC, USA. IEEE Computer Society.
Papaioannou, T. G., Bonvin, N., and Aberer, K. (2012).
Scalia: An adaptive scheme for efficient multi-cloud
storage. In Proceedings of the International Confer-
ence on High Performance Computing, Networking,
Storage and Analysis, SC ’12, pages 20:1–20:10, Los
Alamitos, CA, USA. IEEE Computer Society Press.
Qu, Y. and Xiong, N. (2012). Rfh: A resilient, fault-tolerant
and high-efficient replication algorithm for distributed
cloud storage. In Parallel Processing (ICPP), 2012
41st International Conference on, pages 520–529.
Sachdev, A. and Bhansali, M. (2013). Enhancing cloud
computing security using aes algorithm. International
Journal of Computer Applications, 67(9):19–23. Full
text available.
Srivastava, S., Gupta, V., Yadav, R., and Kant, K. (2012).
Enhanced distributed storage on the cloud. In Com-
puter and Communication Technology (ICCCT), 2012
Third International Conference on, pages 321–325.
Stefanov, E. and Shi, E. (2013). Multi-cloud oblivious stor-
age. In Proceedings of the 2013 ACM SIGSAC Confer-
ence on Computer & Communications Security,
CCS ’13, New York, NY, USA. ACM.
Wang, Q., Wang, C., Ren, K., Lou, W., and Li, J. (2011).
Enabling public auditability and data dynamics for
storage security in cloud computing. Parallel and Dis-
tributed Systems, IEEE Transactions on, 22(5).
SECRYPT2015-InternationalConferenceonSecurityandCryptography
368
