
Measurement of the Distributed Strain and Temperature by
Modeling the Brillouin Spectrum
Mohamed Bouyahi, Amira Zrelli, Houria Rezig and Tahar Ezzedine
Communication System Laboratory Sys’Com, National Engineering School of Tunis,
University Tunis El Manar, BP 37, belvedere 1002, Tunis, Tunisia
Keywords: Stimulated Brillouin Scattering (SBS), Distributed Temperature Sensors, Optical Fiber Sensors.
Abstract: Actually, Structural health monitoring (SHM) presents an important field of researches, since we can
monitor many civil structures using optical fiber sensors which give us the opportunity to explore the effect
of shifting many parameters to detect and measure the influence of both temperature and strain in sensing
fiber, we choose to work on Brillouin-scattering-based distributed sensor. In this paper, we make out the
influence of shift temperature and strain in Brillouin scattering. The study proves the importance of
Brillouin coefficients by fixing all of them. The Brillouin Spectrum will be modulating with Matlab codes.
1 INTRODUCTION
The progress of optical fiber technology and
applications in recent years has improved in the
SHM which has
an important role in the construction
phase and service stage. Lots of parameters, such as
temperature, displacement, strain and material
corrosion, are monitored to evaluate the safety of the
structure. Optical fiber is sensible by many kinds of
parameters (temperature, strain, pression, shape) and
optics (refractive index, mode conversion). In this
case, we choose to detect temperature and strain
variation using optical fiber potentially over long
distances. Whenever temperature or strain change,
optical fiber detects this variation, the refractive
index of silica (material of optical fibers) precisely
changes in response to such variation. In Optical
fibers, there are two nonlinear scattering phenomena
which can be investigated: Stimulated Raman
Scattering (SRS) and Stimulated Brillouin Scattering
(SBS) and both are related to vibration excitation
modes of silica. In this work we concentrate on
studding SBS, which is observed at high guided light
intensity, and affected by the change in refractive
index. This change is recognized through the
Brillouin shift. By measuring the change in Brillouin
shift, the distribution of temperature and strain over
long distances can be obtained, hence coined as
distributed fiber sensors (Singh and Gangwar, 2007).
The vital fiber optic technologies which are
developed for sensor applications are the distributed
fiber optic sensing (Azizan and Shahimin, 2012) and
(Singh and Gangwar, 2007). Distributed sensing,
specially the one using Brillouin signal, is able to
extract many information such as temperature and
strain along the sensing fiber. The information
extracted is highly concrete.
The goal of the sensor optical fiber is to
determine the physical parameters of a fiber
position. The distributed sensors optical fiber is
important in monitoring of the broad structures
(Bridge, Tunnel).
Detecting strain or temperature variation over
small region can be considered as complicated. In
this work we choose to limit our measurement to
20Km, then distributed sensor is the most useful
model in long distance. So, long measuring time is
needed to achieve distributed measurement. The
characteristics of BOTDR (Brillouin Optical Time
Domain Reflectometry) help us to measure strain
and temperature along arbitrary regions. BOTDR is
a distributed optical fiber strain sensor whose
operation is based on Brillouin scattering.
BOTDR is a coherent detection method using a
pulsed light. The main idea is to launch a light into
the optical fiber and then generate spontaneous
Brillouin scattering Therefore, the Brillouin
scattering occurs when the aquastic wave
propagating within the fiber, interact with the light.
It causes a frequency shift of the backscattered
36
Bouyahi M., Zrelli A., Rezig H. and Ezzedine T..
Measurement of the Distributed Strain and Temperature by Modeling the Brillouin Spectrum.
DOI: 10.5220/0005562600360041
In Proceedings of the 6th International Conference on Optical Communication Systems (OPTICS-2015), pages 36-41
ISBN: 978-989-758-116-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

spectrum into two components Stokes and anti-
Stokes.
Scattered Photons light can then either make
energy when there is absorption of acoustic phonons
(Anti-Stokes component) or lose energy in the event
of emission of phonons (Stokes component).
The simulation of Brillouin Spectrum is an
intense research subject notably for sensors’
applications also in systems of transmission by
optical fiber. However, modelisation of both
temperature and strain’s influence (through
coefficients of C
, C
) is not well explored. These
sensing coefficients are usually obtained by the
calibration measurement of Brillouin spectrum. Also
by analyzing the distorted Brillouin spectrum,
strain’s information can be found.
This paper focuses on the development of a
simulation model using MATLAB for a distributed
Brillouin spectrum fiber optic sensor. SBS is
specifically implemented. We will present the
Brillouin gain spectrum which is depicted by each
value of the frequency difference.
2 BRIEF THEORY AND
METHODOLOGY
Structural health monitoring (SHM) has many tools
which are used to detect damage in different
structures: one of the most promising tools is
Scattering mechanism Optical Fiber (OF). This
mechanism has a high durability, immunity to
electromagnetic interference and exact
measurement.
2.1 Scattering Mechanisms
When we speak about optical fiber, we mean a
cylindrical dielectric waveguide (non conducting
waveguide) that transmits light along its axis, based
on the reflection process.
The physical parameters of optical fiber can be
affected by temperature and strain. So the fiber
sensors are able to detect the variation of
temperature and strain over long distances.
These parameters have become the essence of
distributed fiber optic sensing. The Rayleigh,
Raman, and Brillouin scattering represent the basic
scattering mechanism of the distributed sensing
techniques which commonly occurred inside the
fiber. The distributed fiber sensing is a really
attractive technique for structural health monitoring
(SHM). It provides information of strain and
temperature about a section or the complete structure
with durability, robustness and measurement
reliability. The distributed optical fiber sensing
systems give us the opportunity to determine
physical parameters. When large structures are to be
monitored, such as bridges, dams and tunnels, this
mechanism can be suitable.
We will demonstrate that both the bandwidth of
Brillouin gain (and the intensity of Brillouin
scattering light) and Brillouin frequency shift have
good linear relationship to the strain and temperature
of the optical fiber, which can realize simultaneous
temperature and strain measurement by using one
optical fiber, with a lower accuracy.
A pulse of laser is launched into the fiber, we
amplify the input signal pulse in an optical fiber in a
similar way as it undergoes in EDFAs, erbium-
doped fibre amplifiers. The directional coupler is
backscattering the light to the same fiber to measure.
The pulse propagates along the fiber to the receiver.
The backscattering of light is resumed of the
scattering of incident photon in the fiber by the
acoustic photon of the medium. This mechanism
generates the frequency shift when we are measuring
the temperature and strain.
Figure 1 : Optical Time Domain Reflectometer functional
schematic.
The backscattering signal refers to the Stokes
frequency of the Stimulated Brillouin Scattering
(SBS) and the occurrence of the bathochromic shift
(the Stokes component) w
=w
−w
with respect
to the pumping beam, where w
denotes acoustic
photon of the fiber. The fundamental difference
from Brillouin and Raman scattering is the
interaction of light photon with acoustic phonons in
contrast with the Raman scattering where there is an
interaction between light photons and molecular
vibrations. The frequency of acoustic photon is
determined by the following formula (Halina, 2005).
w
=
4πn
v
λ
(1)
Pulsed Laser
Receiver
Data Acquisition System
Processor
MeasurementoftheDistributedStrainandTemperaturebyModelingtheBrillouinSpectrum
37
v
indicates the speed of sound in optical
waveguide
n is a refraction index.
As a result of interaction between the matter and
light photons the energy exchange occurs via
acoustic photons leading to the third-order
polarization of the medium.
P
()
= χ
()
E
E
E
(2)
Figure 2: Scheme of Brillouin Scattering.
E
and E
are states that correspond to the
electronic states; the states are enumerated with the
quantum numbers which denotes the vibration
states. This occurs when a photon of light with
energy of ħw
is lower than the resonance energy
ΔE = E
−E
(Hui and and O’Sullivan, 2009).
2.2 Project Methodology
ε
=
F
E∗A
(cos
θ
−sin
θ
)
(3)
The variation is detected by sensor Fiber Brillouin is
which is based on . F is the force applied by
concrete, A is the surface of optical fiber, E Young
Module and θ the direction of light in the fiber (Luo
and Hao, 2013).
The Brillouin Frequency Shift (BFS) of back
scattering is linearly sensitive to strain and
temperature.
It’s expressed by:
∆V
(
T, ϵ
)
=C
∆T + C
ε
(4)
When ∆
(
,
)
is the variation of Brillouin
Frequency Shift;
,
are the sensing coefficients
of temperature and strain, is the strain variation
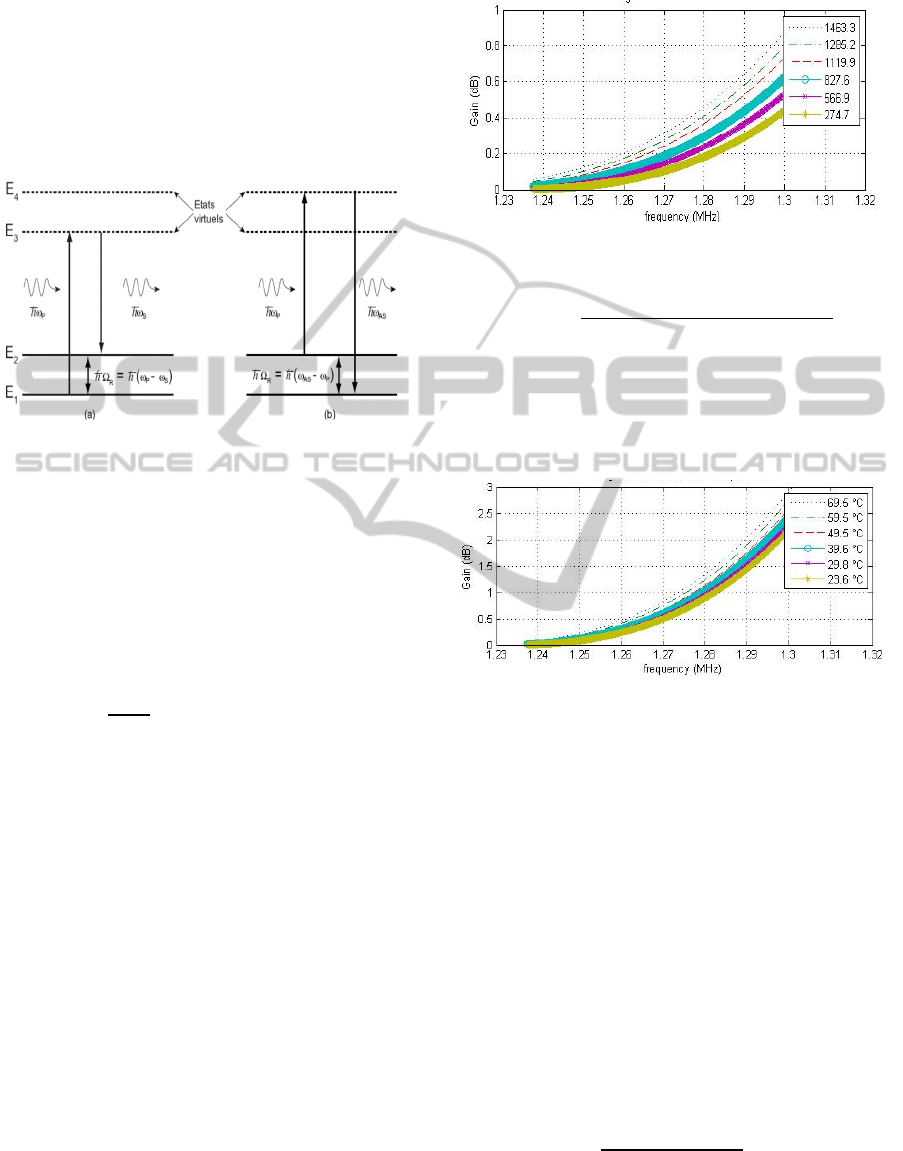
and ∆ is the temperature variation. In the Fig. 1 we
fixed the strain between 274.7 and 1463.3 μ
with
variation of the frequency between 1.23 and 1.32
MHz. In the Fig. 4 we fixed the temperature between
23.6 and 69.5 ° with variation of the frequency
between 1.23 and 1.32 MHz.
Figure 3: Gain with Fixed Strain.
g
(
w
)
=g
(∆V
(
T, ϵ
)
/2)
(w
−w
)
+(∆V
(
T, ϵ
)
/2)
(5)
Where
(
)
is the Brillouin gain and is calculated by
=
−
, and means that =w
. The w
denotes the
Frequency Brillouin shift. When there is a propagation of
the signal with attenuation the gain increases.
Figure 4: Gain with Fixed Temperature.
The Fig 3 and 4 are modified with a small
variation of strain or temperature or both. The
refractive index is linearly dependent on the
temperature and strain of the fiber. The acoustic
velocity that depends on temperature and strain can
also be solved using
and refractive index that is
dependent on temperature and strain (Liu and Bao,
2012).
Let us consider an interaction between the
pumping and the Stokes beams of the intensities I
and I
, respectively. Let us assume that they
represent continuous waves CW (or quasi-CW). The
intensities of the beams can be characterized by the
following system of equations (Halina, 2005).
I
(
L
)
=I
(
0
)
exp
(
g
(
Ω
)
I
L
−α
L
)
(6)
L
=
1 − exp(−α
L)
α
(7)
OPTICS2015-InternationalConferenceonOpticalCommunicationSystems
38

I
(
L
)
the intensity stokes depend of the length of
fiber.
L
the length of effective fiber.
L refers to length of real fiber.
The intensities of the beams by length of fiber
can be characterized by the following system of
equations.
dIs
dz
=−g
(
Ω
)
Ip
(
L
)
Is
(
L
)
+α
Is(L)
(8)
dIp
dz
=−
w
w
g
(
Ω
)
Ip
(
L
)
Is
(
L
)
−α
Ip
(
L
)
(9)
The progress of Brillouin Scattering in optical
fiber is governed by a set of two inter-related
equation under steady-state condition (Azizan and
Shahimin, 2012) and (Singh and Gangwar, 2007).
The
Ip
(
L
)
, Is
(
L
)
, g
(
Ω
)
, α
and α
represent the pump intensity, the Stokes intensity,
the Brillouin Gain coefficient, coefficients
describing loss in an optical fiber for the Stokes and
the pumping beams.
3 FEASIBILITY ANALYSIS AND
ERROR EVALUATION OF
BOTDA BASED
SIMULTANEOUS STRAIN AND
TEMPERATURE
MEASUREMENT
ε
=ε+
(
α
+α
)
.∆T
(10)
In this session we simulate the error of the concrete
and steel, ε
which represents the value of error
(Sikali, 2012). ε represents the value of strain, α
is
the value of steel, α
is the value of concrete and ∆T
the value of temperature.
In our simulation we fixed the coefficient of
Brillouin Frequency Shift by C
(
ϵ
)
andC
(
ϵ
)
.
C
(
ϵ
)
= [0.048 ∗ (1
+
[
4.16 ∗ 10
±2.29
∗10
]
∗∆T)]
MHz
μ∈
(11)
C
(
ϵ
)
=
[
1.06 ∗
(
1
+
[
2.73 ∗ 10
±2.04
∗10
]
∗ϵ
)]
MHz
°C
(12)
∆V
´
(
T, ϵ
)
=∆V
(
T, ϵ
)
∗
(
1+β∗R
)
(13)
The ∆V
´
(
T, ϵ
)
is the variation of Brillouin
Frequency Shift with error. ∆V
(
T, ϵ
)
is the
Brillouin Frequency Shift (He and Zhou, 2014), β
bruit variation and random value R between [-1, 1].
Figure 5: Error with Fixed Strain.
Figure 6: Error with Fixed Temperature.
In Fig 5 and 6 we calculate the error obtained by
Brillouin Frequency Shift with error mines Brillouin
Frequency Shift.
Table 1: Variation of BFS and Brillouin Wavelength under
temperature and strain loads.
Strain
(με)
Temp.
(°C)
Variation of
BFS(MHz)
R
500 10 17
0.846221
1000 20 34
-0.525152
1500 30 51
0.202647
2000 40 68
-0.672137
2500 50 85
-0.838118
3000 60 102
0.01964
3500 70 119
0.681277
4000 80 136
-0.379481
4500 90 153
0.831796
5000 100 170
0.502813
5500 110 187
0.709471
6000 120 204
-0.428892
This parameter of simulation is selected for one
simulation; the Brillouin Frequency Shift is
theoretically calculated. The random value R is
generated by the Matlab Software. The level noise
MeasurementoftheDistributedStrainandTemperaturebyModelingtheBrillouinSpectrum
39

signal β are 1%, 2%, 3% 4% 5% and 8%. Fig. 5 and
6 show the strain and temperature applied on the
Brillouin sensor decoupled by Eq. (13). It can note
the value of the strain decoupled by the noise which
agrees well with the theoretical value.
4 RESULTS AND DISCUSSION
To verify the accuracy of simulation, the pump and
the stokes waves propagation over a 30 km-long
fiber, we focused on the same value used in the
(Belal and Newson, 2012)
, (Azizan and Shahimin,
2012) and (Singh and Gangwar, 2007) for all
simulation parameter. We choose the pump power,
P
(
0
)
=4.2mW, the Brillouin gain coefficient,
g
=1.2∗10
m/W, the mode effective area,
A
=86μm
, the fiber attenuation constant, α
=
α
= 0.217dB/km , and the initial Stokes intensity,
P
(
0
)
= 1.726mW. The Fig. 7 shows the results of
the simulations, that the graph published in (Azizan
and Shahimin, 2012) and (Singh and Gangwar,
2007).
The pump power and Stokes power depend on
the length of the fiber. These powers are calculated
by the next equation:
P
(
z
)
=P
(
0
)
∗exp(−α
∗z)
(14)
P
(
z
)
=P
(
0
)
∗exp(−α
∗z)
(15)
P
=A
∗I
(16)
P
=A
∗I
(17)
Figure 7: Pump and Stokes wave evolution over 30 km-
long.
Fig. 7: shows that the output power is in terms of
fiber length, so it is clear that when the fiber length
increases, more signal power (pump and Stokes)
decreases.
The results obtained demonstrate that the power
vanishes from 20 Km long.
Figure 8: Stokes Power.
The attenuation of signal is depends on initial
power stokes. When the initial power is high the
signal is weak. The upper curve mean to the initial
intensity of Stokes is to 74.7 mW, the middle curve
means that the initial intensity of Stokes is to 48.6
mW and the lower is 9.12 mW.
Figure 9: Spectrum of Brillouin.
The spectrum of Brillouin obtains her peak of
frequency w
at 1.247 (GHz).
5 CONCLUSIONS
The effects of temperature and stain shift on
Brillouin scattering in optical fiber have been
descripted. Brillouin spectrum is sensitive to the
frequency’s variation.
So to modulate this spectrum, we choose to fix
the Brillouin coefficients through fixing temperature
or strain and shifting one of them. This study gives a
view how to model and measure Brillouin scattering.
In Structural Health Monitoring, many
parameters over and above temperature and strain
can be studied, such as presion, humidity, etc. So we
have the opportunity to add other parameters using
fiber bragg.
OPTICS2015-InternationalConferenceonOpticalCommunicationSystems
40

REFERENCES
Belal, M., Newson, T.P., 2012 “Experimental
Examination of the Variation of the Spontaneous
Brillouin Power and Frequency Coefficients Under the
Combined Influence of Temperature and Strain”,
Journal of Lightwave Technology.
Azizan, S., Shahimin, M.M., Murad, S.A.Z., 2012 “Simple
Distributed Brillouin Scattering Modeling for
Temperature and Strain Sensing”, IEEE Symposium on
Business, Engineering and Industrial Applications.
He, J., Zhou, Z., Ou, J., 2014 “Simultaneous measurement
of strain and temperature using a hybrid local and
distributed optical fiber sensing system”,
Measurement.
Luo, J., Hao, Y., Ye, Q., Hao, Y., Li, L., 2013
“Development of Optical Fiber Sensors Based on
Brillouin Scattering and FBG for On-Line Monitoring
in Overhead Transmission Lines”, Journal of
Lightwave Technology.
Sikali Mamdem, Y., 2012 “sensors with optical fibers
distributed by Brillouin effect: separation of the
dependence at the temperature and the strain”.
Singh, S. P., Gangwar, R., Singh, N., 2007 “non linear
scattering effects in optical fibers”, Progress In
Electromagnetics Research, PIER.
Reshak, A. H., Shahimin, M. M., Murad, S. A. Z., Azizan,
S., 2013 “Simulation of Brillouin and Rayleigh
scattering in distributed fibre optic for temperature and
strain sensing application”, Sensors and Actuators A:
Physical.
Hui, R., O’Sullivan, M., 2009 “Fiber Optic Measurement
Techniques”, Elsevier Academic Press.
Halina, A., 2005 “nonlinear phenomena in optical fibers”.
Liu, X., Bao, X., 2012 “Brillouin Spectrum in LEAF and
Simultaneous Temperature and Strain Measurement”,
Journal of Lightwave Technology.
MeasurementoftheDistributedStrainandTemperaturebyModelingtheBrillouinSpectrum
41
