
Revisiting Gradient Methods in Function Space
With Application to Rocket Trajectories
Joseph Z. Ben-Asher
Faculty of Aerospace Engineering, Technion, 32000, Haifa, Israel
Keywords: Optimal Control, Green’s Function, Gradient Methods, Rockets Trajectories, Function Space.
Abstract: The gradient method in function space is revisited and applied to the problem of optimizing the trajectories
of aerodynamically maneuvering rockets. The optimization objective may be the maximal range or the
minimal control effort for a given range. The method is shown to provide an implementable and fast
algorithm for a good approximation to the optimal solution. It does not require any non-linear programming
solver, and can be straightforwardly programmed in a flight computer. The method can also be used to
provide an initial guess for more precise techniques, thus accelerating the computational process.
1 INTRODUCTION
Numerical techniques for solving optimal control
problems fall into two general classes: indirect
methods and direct methods. In an indirect method
(Bryson and Ho, 1975; Kelley, 1962; Stryk and
Burlich,1992; Keller, 1968), we rely on the
Minimum Principle and other necessary conditions
to obtain a two-point boundary-value problem
(TPBVP), which is then numerically solved for
optimal trajectories. The main advantages of indirect
methods are their high solution accuracy and the
guarantee that the solution satisfies the optimality
conditions. However, indirect methods are
frequently subject to severe convergence problems.
Frequently, without a good guess for the missing
initial conditions, and a priori knowledge of the
constrained and unconstrained arcs, convergence
may not be achieved at all, or may require some very
long and tedious computational effort. In the direct
methods (Stryk, 1993; Benson, 2004;
Elnagar et.
al., 1995; Fraroo and Ross, 2001; Rao, et. al. 2010)
the continuous optimal control problem is
parametrized as a finite dimensional problem. Well-
developed algorithms for constrained parameter
optimization - also called non-linear programming
(NLP) solvers for historical reasons - then solve the
resulting optimization problem numerically. There
are several popular methods which transform the
optimal control problem into a parameter
optimization problem. In present time the most
popular methods are the collocation method and
pseudo-spectral methods. Numerical optimization of
the constrained parameter optimization typically
involves finding hundreds of unknown parameters
subject to hundreds of constraints. The computation
time, especially when the initial guess is far from the
solution, may become quite significant. This fact
may be critical for real-time applications or in
applications where the solution is needed for a huge
number of cases (say with various terminal
conditions).
Gradient in function space (Kelley, 1962; Bryson
and Denham 2010) is a well-known method which
may be characterized as a hybrid method, merging
direct and indirect methods. On the one hand
necessary conditions for the adjoint system are met,
whereas on the other hand the control function is
directly sought by the method of gradients. The
control function is iteratively updated based on the
current state/adjoint solution by evaluating the
corresponding Green’s function and using gradient
correction (steepest descent) in function space. No
further NLP solvers are needed for the solution.
Guided rocket is a new field in rockets development,
which offers several improvements such as
extensions of existing rockets range, improved
accuracy, trajectory shaping, etc. These
improvements are achieved by providing the rockets
maneuverability either by aerodynamics means or by
using small pyrotechnical motors (pulsers). Some
approximate methods have been employed in the
past to this problem (e.g. Kelley et. al., 1982).
However, finding the optimal trajectories for rockets
270
Ben-Asher J..
Revisiting Gradient Methods in Function Space - With Application to Rocket Trajectories.
DOI: 10.5220/0005562702700274
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 270-274
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

is still an important challenge. The computation time
in these applications is of a particular importance for
two main reasons: (a) fast calculation of trajectories
is needed just before launching a rocket to a new
target; (b) real time corrections in flight might be
required due to disturbances and/or target
movement.
The main purpose of this work is to revisit the
gradient method in function space in order to obtain
easily implementable and fast, albeit less accurate,
trajectories for maneuvering rockets. The method
can be used either by itself or as an accelerating
method for more accurate techniques.
2 GRADIENTS IN FUNCTION
SPACE
For completeness will present here the methods of
gradient based on (Kelley, 1962). Consider the
following state-space representation of a dynamic
system:
)),(),(()( ttutxgtx
(1)
Where x(t) and u(t) are n-dimensional and m-
dimensional vectors, respectively. For a given initial
condition, we want to minimize some terminal cost
P(x
f
). For simplicity, let us assume that t
f
is
specified. Let u(t) and x(t) be some guess values for
the state and control variables respectively, and
consider a sufficiently small variation δu(t) and the
resulting δx(t) determined by the linearized
equation:
0
() () () () (); ( ) 0
TT
xu
xt g t xt g t ut xt
(2)
Where g
u
and g
x
are Jacobian matrices. Consider
now the adjoint system, defined by the linear time-
varying differential equations:
() () ()
x
tgtt
(3)
One can readily obtain, using (2) and (3), that:
(()())
() () () ()
() () ()
T
TT
TT
u
dtxt
dt
txt txt
tg t ut
(4)
On the other hand, the cost variation can be written
(to first order) as:
PPx
x
T
f
f
(5)
where P
xf
if the gradient of P with respect to x
f
.
Using Eq. (3), with the following terminal
conditions,
()
f
f
x
tP
(6)
we get, from Eq. (4) and Eq. (5), and the fact the
initial condition is given, that
0
0
(()()) ()
() ()
f
f
t
T
u
t
t
T
t
P
gt t utdt
tutdt
(7)
The term µ(t) is the gradient of the cost in the
control function space (Courant and Hilbert, 1953).
Under control iterations, the steepest descent will be
in its negative direction. This fact can be easily
derived from Schwarz’s inequality, as follows:
0
00
2
2
22
() ()
() ()
f
ff
t
T
t
tt
tt
Ptutdt
tdt utdt
(8)
For the case µ(t) ≠0 the upper limit on the left is
obtained (under equality) for
() ()ut k t
(9)
k is any constant real number. For the minimization
of P, this constant should have a sign opposite to the
sign of function space.
Hence µ(t) is in the (current) direction of the
gradient in function space. For a different derivation
the reader is referred to (Kelley, 1962). Notice that
for the case µ(t)=0 the optimal control cannot be
determined by this method!
3 MAXIMAL ROCKET RANGE
3.1 Problem Formulation
The dynamic modeling of a lifting rocket will be
introduced first. For simplicity, post-boost dynamics
in a flat earth 2-D scenario is assumed, governed by
the following continuous dynamic equations:
22
0
2
()
2
sin
cos
2
sin
cos
DL
L
VS C KC
V
m
g
VSC
g
mV V
hV
RV
(10)
RevisitingGradientMethodsinFunctionSpace-WithApplicationtoRocketTrajectories
271

R is range, h is altitude, V is velocity, γ is the flight-
path angle, m is mass, S is a reference area, α is the
angle of attack, ρ is air density; g is gravity, C
D0
and
K are the parabolic drag coefficients, and finally C
Lα
is the lift slope coefficient.
The control in this problem is the angle-of-attack
α. It assumed to be changed instantaneously without
any time delay (point mass approximation).
Increasing the angle-of-attack creates the required
lift force, but it also increases the induced drag.
The maximal range problem is to minimize the
following cost by the control for a given x(0):
() ()
f
f
Pt Rt
(11)
Remark: Notice that t
f
is not specified; in practice we
should find it by the terminal condition of reaching
the ground (see below).
3.2 The Adjoint System and Green’s
Function
From (3) and (10) we readily obtain the following
adjoint system:
2
cos
(sin
2
cos )
sin
(cos
cos sin )
2
0
L
vh
D
vR
h
vR
hLvD
R
SC
g
mV
VSC
m
g
V
V
gV
SV d
CCV
mdh
H
R
(12)
λ
i
is the adjoint (co-state) associated with the state
variable i. As already explained, in the gradient
method we use a present guess for the control, the
state and the adjoint variables, where the terminal
conditions for the adjoints (in this maximal range
problem) are all zeros except for λ
R
which is 1 (from
Eq. 6). The Green’s function for this problem
becomes:
2
2
1
() () ()
2
L
VL
V
tSKCtVSCt
mm
(13)
The control function is updated, as follows:
(14)
The scalar k is some positive fixed number which
determines the step size.
As the terminal time is unknown, we also update its
value in order to obtain h(t
f
)=0, thus:
)()(
ff
old
f
new
f
ththbtt
(15)
where b is some positive fixed number. We iterate
on the problem by resolving Equations (10) – (15)
until some convergence condition is satisfied.
3.3 Computational Results
A fictitious 140 kg rocket with 94 km non-lifting
range is considered. The initial end-of-boost angle is
fixed to 53 deg. and the rocket flies a non-lifting
trajectory up to its apogee. The maximal angle-of-
attack is set to 15°. The lift coefficient is CLα=8
with the reference area of 0.0405 m
2
; and the drag
coefficients C
D0
and K are 0.14 and 0.127,
respectively. It is required to extend the range to its
maximum (with the initial conditions set at the
apogee). Fig. 1 presents in blue the optimal
trajectories obtained by two direct approaches:
GPOPS (Rao et. al. 2010) and the cubic-spline based
collocation method (Stryk, 1993). Also shown in red
is the trajectory obtained by the gradient-in-
function-space method. The first two solutions
overlap and their maximal range is identical 171km.
The gradient-in-function-space solution reaches
somewhat shorter range (169 km) hence it should be
considered sub-optimal. The optimal flight time is
313 sec.
Remark: The NLP solver for GPOPS was NPOPT or
IPOPT, whichever runs faster. The NLP solver for
the collocation method was IPOPT. As already said,
the gradient method does not use any NLP solver.
The CPU computation times for this example were
as follows: 27.4 sec for GPOPS; 35 sec for the
collocation method; and only 2.4 sec for the gradient
method. Note that these computation times are based
on MATLAB implementations on an INTEL CORE
i7vPro, hence are far from being minimal (efficient
coding can reduce it by orders of magnitude).
Evidently one can consider them only on a
comparative basis. There is at least one order of
magnitude saving in the computation time for the
gradient method. This result has been obtained in
numerous other examples. At the very least it can be
used as an accelerating method for the other
approaches (Bryson, 1999). Trials based on this idea
have reduced the computation time for the
collocation method by a factor of three.
)()()( tktt
oldnew
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
272
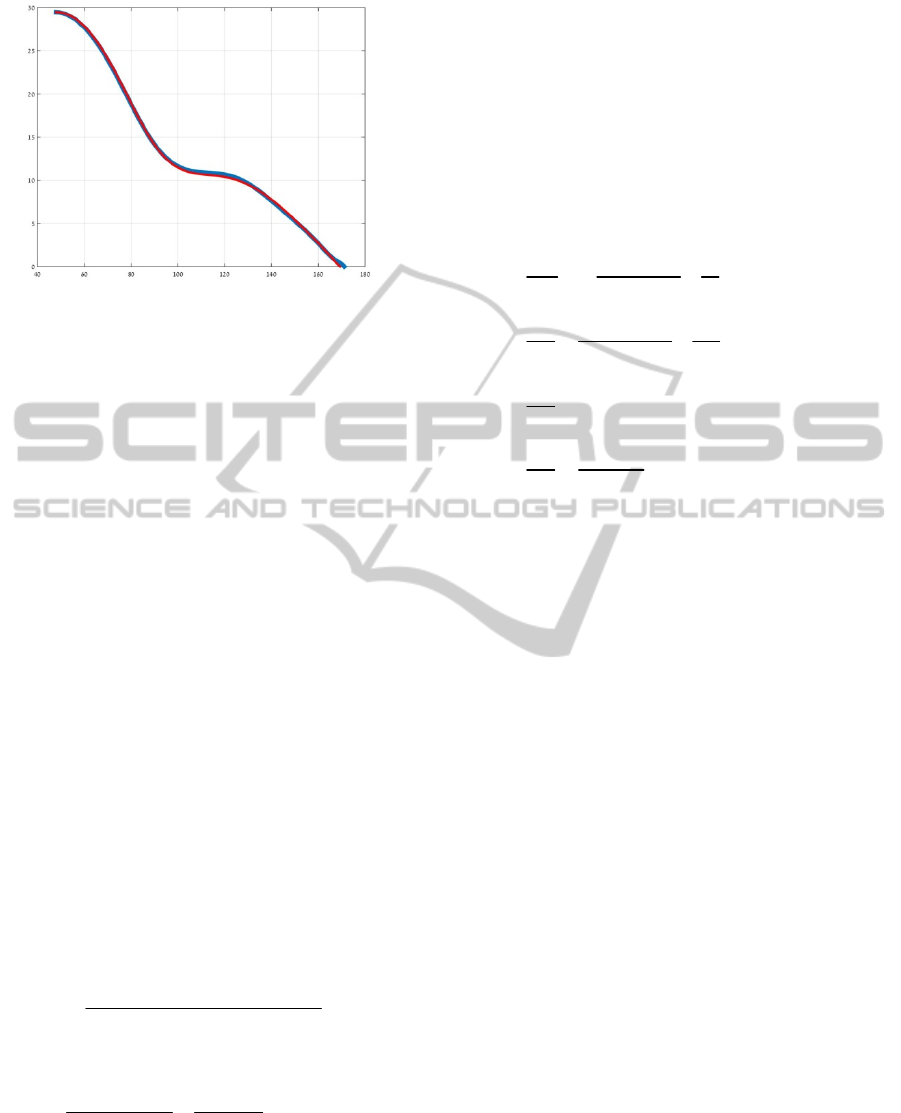
Figure 1: Maximal range trajectories.
4 FIXED ROCKET RANGE
4.1 Problem Formulation
In most practical applications the range of the rocket
is fixed. The optimization problem is therefore
aimed at a different cost function. One plausible
candidate is the control effort. The reasons are
threefold:
a. The domain of static stability is typically
small for rockets and they may stall at
even medium angle-of-attack values.
b. Wind gusts may increase the effective
angle-of-attack causing even earlier stall
conditions.
c. It will also minimize the requirements
from the servos activating the control
surfaces.
Hence the following cost will be considered:
2
0
()
f
t
J
tdt
(16)
To obtain a Meyer’s formulation, a 5
th
state
representing the accumulated control effort is
introduced. Thus the system becomes:
22
0
2
2
()
2
sin
cos
2
sin
cos
0.5
DL
L
VSC KC
V
m
g
VSC
g
mV V
hV
RV
P
(17)
And the cost is simply the terminal 5
th
state value:
()
f
JPt
(18)
In order to obtain the required range, the problem
can be simplified by changing the independent state
from time to range. This is advisable due to fact that
it behaves monotonically with time and has fixed
initial and terminal values (Kelley, 1962). Dividing
(17) through by
R
the systems equations are reduced
to:
22
2
tan
cos
cos
tan
cos
dV D g
dR mV V
dLg
dR mV V
dh
dR
dP
dR V
(19)
The terminal altitude needs to be zero. To this end
we introduce a penalty function (Kelley, 1962)
2
() () ()
ff f
P
RPRWhR
(20)
for some large positive scalar W
.
4.2 The Adjoint System and Green’s
Function
Similarly to the previous section, the adjoint system
is calculated by (3) with R being the independent
variable. For each iteration we first integrate (19)
forward, and then integrate the associated adjoint
equations backward with two sets of terminal values:
(0 0 0 1) yielding - from (5) - the control-effort
influence function μ
1
(R); and (0 0 1 0) yielding the
terminal altitude influence function μ
2
(R). We then
combine them to obtain a single influence function
for the total cost (21), as follows
12
() () 2 ( ) ()
f
R
RWhR R
(21)
We proceed as before
() () ()
new old
R
Rk R
(22)
The scalar k is some positive fixed number which
determines the step size.
4.3 Computational Results
Fig. 2 presents the trajectories obtained by the
gradient method (red) and by GPOPS (blue), for a
RevisitingGradientMethodsinFunctionSpace-WithApplicationtoRocketTrajectories
273

rocket flying to the fixed range of 140 km. The
flight time is about 190 sec. As seen, the trajectories
are fairly close to each other but the gradient method
results are again sub-optimal, with some
intermediate higher maneuver. This maneuver
entails a total cost of 0.6769 sec, compared with
merely 0.6242 sec of GPOPS. However, the CPU
computation time for the latter was 28 sec, as
opposed to 3 sec for the former.
Figure 2: Fixed range trajectories.
5 CONCLUSIONS
Present day computational methods, in particular
direct methods such as pseudo-spectral and
collocation methods, are widely and successfully in
use. Bryson’s and Kelley’s old but powerful ideas
of Gradients in Function Space are much less used
today, perhaps under the impression that the current
methods are superior and therefore these techniques
belong to the past.
The purpose of this position paper was to
somewhat rectify this impression by claiming that, at
least for fast computations and very simple
implementations, Gradients in Function Space can
still be an invaluable method. The computation time
is, typically, one order of magnitude lower than for
the direct methods, and the implementation (e.g. the
number of code lines needed to perform the
calculations, the required memory size, etc.) is also
much less demanding as no NLP solver is required.
Consequently, the algorithm fits very well with on-
board computations. Optimal rocket trajectory is a
problem where such advantages are important.
ACKNOWLEDGEMENTS
The author wish to thank Dr. Eugene M. Cliff from
Virginia Tech for his useful comments regarding the
manuscript, and Mr. Matthias Bittner from the
Institute of Flight System Dynamics, Technische
Universität München, for his help in producing
efficient collocation results.
REFERENCES
Bryson A. E. and Ho Y-C, Applied Optimal Control,
Hemisphere P. C, 1975, pp. 50-120.
Kelley H. J., "Methods of Gradients", Chapter 6 in
Optimization Techniques ed. G. Leitman, Academic
Press 1962, pp. 218-222.
Stryk O. and Bulirsch R." Direct and Indirect Methods For
Trajectory Optimization", Annals of Operations
Research 37(1992) 357-373.
Keller H. B., Numerical Methods for Two-Point Boundary
Value Problems, Blaisdell, New York, 1968. pp.1-150.
Stryk O., “Numerical Solution of Optimal Control
Problems by Direct Collocation, Optimal Control, ed.
Bulirsch R, Miele A. and Stoer J., Birkhauser Verlag,
Basel, 1993, pp. 129–143..
Benson D. A, Gauss Pseudospectral Transcription for
Optimal Control, MIT Ph. D. Thesis, Department of
Aeronautics and Astronautics, November 2004.
Elnagar J., Kazemi M. A., and Razzaghi M., “The
Pseudospectral Legendre Method for Discretizing
Optimal Control Problems,” IEEE Transactions on
Automatic Control, Vol. 40, No. 10, October 1995, pp.
1793-1796.
Fahroo F. and Ross I. M., “Costate Estimation by a
Legendre Pseudospectral Method,” Journal of
Guidance, Control, and Dynamics, Vol. 24, No. 2,
2001, pp. 270–277.
Rao A. V. et.al., “Algorithm 902: GPOPS, A MATLAB
Software for Solving Multiple-Phase Optimal Control
Problems Using the Gauss Pseudospectral Method”,
ACM Transactions on Mathematical Software, Vol.
37, No. 2, Article 22, April 2010.
Bryson A. E. and Denham W. F. “A Steepest-Ascent
Method for Solving Optimum Programming
Problems,” J. Appl. Mech. 29(2), 247-257, 2011.
Kelley H. J., Cliff E. M. and Lutze, F. H, “Boost–glide
Range-Optimal Guidance,” Optimal Control
Applications and Methods, Volume 3, Issue 3, pages
293–298, July-September 1982.
Courant R. and Hilbert D., Methods of Mathematical
Physics vol.X , Interscience Publishers Inc. 1953, pp.
222-224.
Bryson A. E., Dynamic Optimization, Addison Wesley
Longman, 1999.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
274
