Adaptive Unscented Kalman Filter at the Presence of Non-additive
Measurement Noise
Manasi Das, Aritro Dey, Smita Sadhu and T. K. Ghoshal
Department of Electrical Eng., Jadavpur University, Kolkata, 700032, India
Keywords: Adaptive Filters, Unscented Kalman Filter, Nonlinear State Estimation, Non-additive Measurement Noise.
Abstract: This paper proposes an Adaptive Unscented Kalman Filter (AUKF) for nonlinear systems having non-
additive measurement noise with unknown noise statistics. The proposed filter algorithm is able to estimate
the nonlinear states along with the unknown measurement noise covariance (R) online with guaranteed
positive definiteness. By this formulation of adaptive sigma point filter for non-additive measurement noise,
the need of approximating non-additive noise as additive one (as is done in many cases) may be waived.
The effectiveness of the proposed algorithm has been demonstrated by simulation studies on a nonlinear two
dimensional bearing-only tracking (BOT) problem with non-additive measurement noise. Estimation
performance of the proposed filter algorithm has been compared with (i) non adaptive UKF, (ii) an AUKF
with additive measurement noise approximation and (iii) an Adaptive Divided Difference Filter (ADDF)
applicable for non-additive noise. It has been found from 10000 Monte Carlo runs that the proposed AUKF
algorithm provides (i) enhanced estimation performance in terms of RMS errors (RMSE) and convergence
speed, (ii) almost 3-7 times less failure rate when prior measurement noise covariance is not accurate and
(iii) relatively more robust performance with respect to the initial choice of R when compared with the other
nonlinear filters involved herein.
1 INTRODUCTION
Adaptive state estimation techniques have got more
attention of researchers in recent few years due to
their renowned superiorities (Almagbile, 2010) over
non adaptive state estimators. In this paper an
Adaptive Unscented Kalman Filter (AUKF) has
been proposed which is applicable for the situation
where non-additive measurement noise is present.
In earlier stages adaptive filters were mostly
formulated on linear Kalman Filtering framework
(Mehra, 1972). However recent trends of research
are directed towards adaptive nonlinear estimation
techniques. The earliest adaptive nonlinear filter
reported in literature is Adaptive Extended Kalman
Filter (AEKF) (Busse, 2003; Meng, 2000). AEKF is
found to fraught with dificulties like singularity
problems, complex jacobian calculations (Wan,
2000; Fathabadi, 2009) etc. which further leads
toward an alternate adaptive nonlinear estimation
technique named as Adaptive Sigma Point Kalman
Filter (ASPKF) (Das, 2013). Adaptive Unscented
Kalman Filter (AUKF) (Das, 2014; Soken, 2011;
Chai, 2012), Adaptive Central Difference Filter
(ACDF) (Das, 2015) or Adaptive Divided
Difference Filter (ADDF) (Dey, 2015) all belong to
the class of ASPKF. The present work in this paper
is formulated on Unscented Kalman Filtering (UKF)
framework as it is able to exhibit better estimation
performance compared to Extended Kalman Filter
(EKF) and first order Central or Divided Difference
Filter (CDF/ DDF) (Norgaard, 2000; Ito, 2000).
The proposed filter herein determines the
covariance (R) online of the nonadditive
measurement noise and therefore it fits into R-
adaptive filter category. There are several existing
methodologies of adapting R in literature (Mehra,
1972; Das, 2014). Direct covariance matching
method depending on the innovation or residual
sequence is the simplest and straight forward
technique among them (Mehra, 1972; Mohamed,
1999). The rudimental idea of R adaptation in the
present work is adopted from (Mohamed, 1999)
where direct covariance matching method of
adaptation depending on residual sequence is
utilized for linear signal models.
However, adaptive formulation of sigma point
filters considering non-additive measurement noise
is very rare in literature. In (Dey, 2015) an adaptive
Divided Difference Filter (ADDF) for nonlinear
614
Das M., Dey A., Sadhu S. and K. Ghoshal T..
Adaptive Unscented Kalman Filter at the Presence of Non-additive Measurement Noise.
DOI: 10.5220/0005565306140620
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 614-620
ISBN: 978-989-758-122-9
Copyright
c
 2015 SCITEPRESS (Science and Technology Publications, Lda.)

systems with non-additive measurement noise has
been proposed. Our current work presented in this
paper focuses on adaptive formulation of another
sigma point filter named as Unscented Kalman Filter
(UKF) considering non-additive measurement noise.
To demonstrate the performance of the proposed
filtering algorithm a two dimentional bearing-only
tracking (BOT) problem with non-additive
measurement noise as may be found in (Sadhu,
2006; Lin, 2002) has been chosen. Although in
(Sadhu, 2006; Lin, 2002) the non-additive
measurement noise has been approximated as
additive one, in our current work this approximation
is waived to circumvent the approximation errors. It
may be discerned from the simulation results
presented herein that waiving this additive noise
approximation may enhance the estimation
performance significantly in some particular cases.
The significant contributions of this paper may
be summarized as follows:
 An Adaptive Unscented Kalman Filter (AUKF)
has been formulated which utilizes the
augmented form of UKF and is applicable for
nonlinear systems with non-additive
measurement noise.
 Residual sequencees in lieu of innovation
sequences have been utilized for guaranteed
positive definiteness of the adapted R matrix.
 The proposed algorithm has been exemplified
with a 2-D bearing-only tracking (BOT) test
problem with non-additive measurement noise.
The organization of the paper is as follows.
Section 2 describes the proposed Adaptive
Unscented Kalman Filter (AUKF) in augmented
form applicable for non-additive measurement noise.
In section 3 case studies on 2-D bearing only
tracking (BOT) problem have been illustarted.
Discussions and conclusions are presented in section
4.
2 PROPOSED AUKF
ALGORITHM
2.1 Problem Statement
Nonlinear state estimation problem with non-
additive noise where the prior knowledge of
measurement noise covariance is unavailable is
considered here. The dynamic equations of process
and measurement therefore may be represented by
equations (1) and (2). Where,
n
k
Rx 
,
m
k
Rz 
and
k
w ,
k
v are the non-additive process and
measurement noise with covariance
k
Q and
k
R
respectively.
)w,x(fx
kkk 1

(1)
)v,x(hz
kkk

(2)
Here
k
Q is assumed to be known and constant
(therefore it will be represented by
Q
in the rest of
the paper) whereas
k
R is assumed to be unknown.
The adaptive nonlinear filter designed for this
particular problem is able to adapt the covariance
k
R of the non-additive measurement noise
k
v .
2.2 Filter Algorithm
As non-additive noise is considered here, the
augmented form of UKF (Wan, 2000) has been
utilized here and the adaptive version of augmented
UKF has been formulated. The weight values (Wan,
2000) are calculated as given below:















0i for,
2
1
1
2
00
)n(
WW
)(
n
W;
n
W
a
c
i
m
i
a
c
a
m






(3)
Where,
a
n
is the dimension of augmented state
vector,

is a scaling factor given by
aa
n)n(  
2
, the parameters

and

determines respectively the spread of the sigma
points and a prior knowledge about the noise
distribution. The values of the tuning parameters

,

and

are considered to be 0.5, 2 and 0 in the
present work.
2.2.1 Initialization
Initialize, State error covariance (P
k-1
), Estimated
states (
1
ˆ
k
x
) and measurement noise covariance
(
1k
R
ˆ
).
2.2.2 Prediction (Time Update)
Form augmented state vector as:
1
1













v
w
x
ˆ
x
ˆ
k
a
k
(4)
AdaptiveUnscentedKalmanFilteratthePresenceofNon-additiveMeasurementNoise
615

Where,
w
and
v
are respectively mean of
process and measurement noise and
a
na
k
Rx
ˆ

1
.
Form augmented state error covariance matrix
as:
00
00
00
1
1
1














k
k
a
k
R
ˆ
Q
P
P
(5)
It is assumed here that the state errors, process
noise and the measurement noise are not correlated
to each other. Hence the off-diagonal sub-blocks of
the matrix in equation (5) are considered as zero.
Calculate the sigma points of
a
k
x
ˆ
1
as:
















v
k-
w
k-
x
k-
a
k
a
k
a
a
)n(n
a
k
a
k
a
k-
ˆ
ˆ
ˆ
]PP)n(zeros[
)n(]x
ˆ
.....x
ˆ
[
ˆ
aa
1
1
1
11
12
111
1
X
X
X
X

(6)
Propagate the sigma points (
x
k-
ˆ
1
X
and
w
k-1
ˆ
X
)
through the function f as:
)
ˆ
,
ˆ
(
ˆ
11
w
k-
x
k-k
f XXX 

(7)
Project the state ahead as:





i,k
n
i
m
ik
ˆ
Wx
ˆ
a
X
2
0
(8)
Project the state error covariance ahead as:
})x
ˆ
ˆ
)(x
ˆ
ˆ
{(WP
T
ki,kki,k
n
i
c
ik
a





XX
2
0
(9)
Propagate the sigma points (

k
ˆ
X
and
v
k-1
ˆ
X
)
through the function h as:
)
ˆ
,
ˆ
(
ˆ
,1,,
v
ikikik
h


 XXZ
(10)
Predict the measurement as:
-
Z
k,i
n
i
m
ik
ˆ
Wz
ˆ
a




2
0
(11)
2.2.3 Correction (Measurement Update)
Calculate the innovation covariance as:




a
n
i
T
ki,kki,k
c
izz
})z
ˆ
ˆ
)(z
ˆ
ˆ
{(WP
2
0
ZZ
(12)
Calculate the cross covariance as:




a
n
i
T
ki,kki,k
c
ixz
})z
ˆ
ˆ
)(x
ˆ
ˆ
{(WP
2
0
ZX
(13)
Calculate the Kalman gain as:
1

zzxzk
PPK
(14)
Estimate the state as:
)z
ˆ
z(Kx
ˆ
x
ˆ
kkkkk


(15)
Calculate the estimated state error covariance as:
T
kzzkkk
KPKPP 

(16)
2.2.4 Adaptation of ‘R’
Form augmented state vector
a
k
x
ˆ
by augmenting the
estimated state
k
x
ˆ
with mean of process and
measurement noise as is done in equation (4).
Form augmented state error covariance matrix
a
k
P1
and
a
k
P2
as given below:











mm
k
a
k
I
Q
P
P
00
00
00
1
(17)











1
00
00
00
2
k
k
a
k
R
ˆ
Q
P
P
(18)
Calculate the sigma points:














v
k
w
k
x
k
a
k
a
k
a
a
)n(n
a
k
a
k
a
k
ˆ
ˆ
ˆ
]PP)n(zeros[
)n(]x
ˆ
.....x
ˆ
[
ˆ
aa
1X
1X
1X
1X
111
12

(19)














v
k
w
k
x
k
a
k
a
k
a
a
)n(n
a
k
a
k
a
k
ˆ
ˆ
ˆ
]PP)n(zeros[
)n(]x
ˆ
.....x
ˆ
[
ˆ
aa
2X
2X
2X
2X
221
12

(20)
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
616

Propagate the sigma points (
x
k
ˆ
2X
and
v
k
2X
ˆ
)
through the function h as:
)
ˆ
,
ˆ
(
ˆ
,,,
v
ik
x
ikik
h 2X2XZ 
(21)
Estimate the measurement as:
k,i
n
i
m
ik
ˆ
Wz
ˆ
a
Z



2
0
(22)
Calculate residual as:
kkk
z
ˆ
zres 
(23)
Calculate the residual covariance with in sliding
window (of size ‘ws’) as:
T
i
k
wski
ires
)res)(res(
ws
P



1
1
(24)
Now propagate the estimated state and sigma
points of measurement noise (
v
k
1X
ˆ
) through the
function h as:
)
ˆ
,
ˆ
(
ˆ
,,
v
ikkik
xh 1X1Z 
(25)
Similarly, propagate sigma points of estimated
states (
x
k
ˆ
2X
) and mean of measurement noise through
the function h as:
),
ˆ
(
ˆ
,,
vh
x
ikik
2X2Z 
(26)
Calculate the covariance matrix
T
DD
(this
matrix is analogous to
T
D
RD
of Extended Kalman
Filter where R is considered as unity) as:



a
n
i
T
ki,kki,k
c
i
T
})z
ˆ
ˆ
)(z
ˆ
ˆ
{(WDD
2
0
11 1Z1Z
(27)
Where,
k
z
ˆ
1
is calculated as:
k,i
n
i
m
ik
ˆ
Wz
ˆ
a
1Z



2
0
1
(28)
Find the matrix D by Cholesky factorization of
T
D
D
.
Calculate the covariance matrix C (which is
analogous to
T
H
P
H
of Extended Kalman Filter) as:



a
n
i
T
ki,kki,k
c
i
})z
ˆ
ˆ
)(z
ˆ
ˆ
{(WC
2
0
22 2Z2Z
(29)
Where,
k
z
ˆ
2
is calculated as:
k,i
n
i
m
ik
ˆ
Wz
ˆ
a
2Z



2
0
2
(30)
Estimate ‘R’ as:
11 
 )D)(CP(DR
T
resk
(31)
2.2.5 Comments on the Algorithm
Following specific comments can be made about the
proposed filter algorithm.
 A sliding window has been utilized here to
calculate the residual covariance as shown by
equation (24). However, if the current instant
(k) is less than the window size (ws) defined by
the user, the residual covariance should be
calculated from all the available residual
sequences.
 The window size should be chosen carefully.
Too small window size may lead to quick
adaptation in the cost of noisy performance.
Whereas choosing too large window may
provide very smooth R adaptation
compromising in the speed of adaptation.
 In equation (5)
1k
R
ˆ
has been utilized due to
the unavailability of adapted R at k
th
instant.
Once adaptation of ‘R’ at k
th
instant is
completed, an iteration of the filtering steps can
also be carried out by utilising
k
R
ˆ
. However,
due to increased calculation burden this
iterative structure is not included in the
proposed algorithm.
 Due to the use of augmented state vector and
additional calculation steps for R adaptation,
computation burden of the proposed AUKF is
more compared to normal UKF. But the
effectiveness of the proposed algorithm for
nonlinear state estimation at the presence of
non-additive noise (with unknown noise
statistics) compensates the shortcoming related
to extra calculation burden.
3 CASE STUDY
3.1 2-Dimensional BOT Problem
3.1.1 Process Model
Two dimensional bearing only tracking (BOT)
problem (Sadhu, 2006) consists of two components,
platform kinematics and target kinematics, as shown
in figure 1. The target moves along x axis and the
platform accompanied with a sensor moves parallel
to the target with constant velocity.
AdaptiveUnscentedKalmanFilteratthePresenceofNon-additiveMeasurementNoise
617

Target motion is considered here as the process
model and is given by
)k(w
T
)k(Tx)k(x)k(x
2
11
2
211

(32)
)k(Tw)k(x)k(x  1
22
(33)
Where,
)k(x
1
is target position along x axis and
)k(x
2
is target velocity which is also assumed to be
constant.
T=1 sec. is the sampling time and w(k) is
process noise with covaraiance Q=0.01m
2
/sec
4
.
Values of these parameters are adopted from (Sadhu,
2006).
Figure 1: BOT trajectory.
3.1.2 Measurement Model
Platform position (along x and y axis) and bearing
between
x axis and line of sight from sensor to target
are considered as measurement equations and are
given by:
)k(v)k(y)k(z
p 11
20 
(34)
)k(vkT)k(x)k(z
p 22
4 
(35)
)k(v
)k(vkT)k(x
)k(v
tan
)k(v
)k(x)k(x
)k(y
tan)k(z
p
p
3
21
1
1-
3
1
1-
3
4
20























(36)
First two measurement variables are the platform
positions along
y axis and x axis respectively. ‘k’ is
the current time instant. It is evident from the
measurement model that the third measurement
variable is a nonlinear function of state as well as the
measurement noises (
)k(v
1
and
)k(v
2
). However,
)k(v
3
is the additive measurement noise.
Measurement noise vector
v therefore may be
formed as [
)k(v);k(v);k(v
321
] with true
covariance
R
k
. Where R
k
is given by:











2
3
2
2
2
1
00
00
00
v
v
v
k
R



(37)
1v

,
2v

and
3v

are the standard deviation of
three measurement noises with nominal values of 1
meter, 1 meter and

3
respectively. All initial values
of the model and the filters are same as in (Sadhu,
2006).
3.2 Simulation Results
To assess the performance of the proposed filter, it
has been compared with non adaptive UKF, AUKF
with additive noise (Chai, 2012) approximation and
ADDF for non-additive noise (Dey, 2015). For
AUKF with additive noise (Chai, 2012), the non-
additive measurement noise has been approximated
to additive one in the same way as is done in (Sadhu,
2006). When the appropriate knowledge of
measurement covariance (
R) is available, it has been
found that performances of all the considered
filtering algorithms are closely comparable. Since
the main aim of the paper has been to propose an
adaptive algorithm when the proper knowledge of
measurement noise covariance (
R) is unavailable,
the results presented here have considered the prior
knowledge of
R as wrong. Two simulation scenarios
have been considered here (i) when prior knowledge
of
R is scaled up (true R X 100) and (ii) when prior
knowledge of R is scaled down (true R / 100). Figure
2, 3 and 4 shows respectively the RMS errors of
position, velocity and track losses (as defined in
(Sadhu, 2006)) for 10,000 Monte Carlo runs when
prior knowledge of
R is (true R) X 100.
Figure 2: RMSE of position (m) when prior knowledge of
R is (true R) X 100.
1
10
100
0 5 10 15 20
Time (sec.)
RMSE of position (m)
UKF
Augmented AUKF
AUKF w ith additive noise
A DDF
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
618

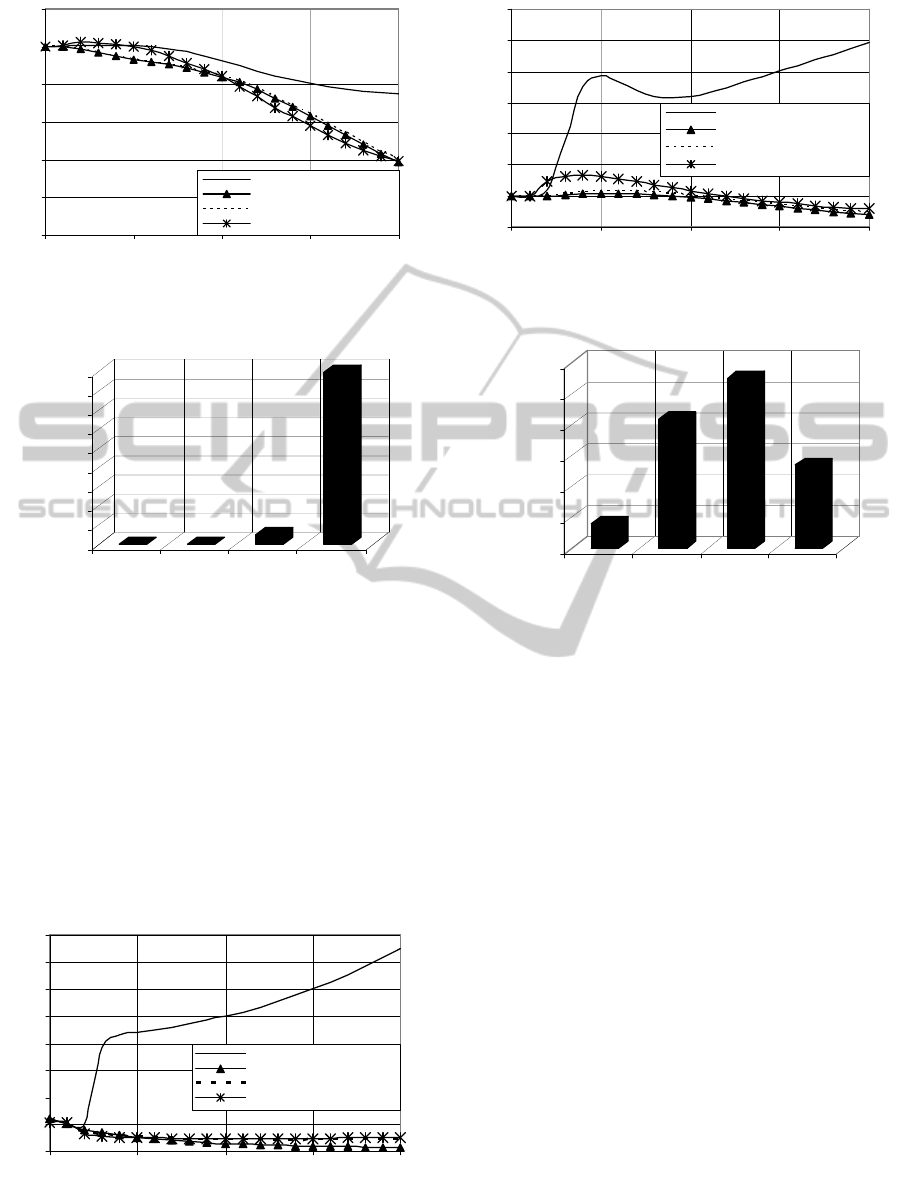
Figure 3: RMSE of velocity (m/sec.) when prior
knowledge of R is (true R) X 100.
Figure 4: Number of track losses when prior knowledge of
R is (true R) X 100.
Figure 4, 5 and 6 shows respectively the RMS
errors of position, velocity and track losses for
10,000 Monte Carlo runs when prior knowledge of
R
is (true
R) / 100.
It may be found from all these simulation results
that the proposed adaptive filter provides less RMS
errors compared to the other filtering algorithms
involved in both the simulation scenarios. Track loss
counts are also less in the proposed filter algorithm
compared to the other filtering algorithms involved.
Figure 5: RMSE of position (m) when prior knowledge of
R is (true R) / 100.
Figure 6: RMSE of velocity (m/sec.) when prior
knowledge of R is (true R) / 100.
Figure 7: Number of track losses when prior knowledge of
R is (true R) / 100.
The chosen 2D-BOT problem is infamous for the
track loss problem associated with it. However it has
been found that the track loss counts (failure rate) in
the proposed Adaptive UKF is less in all simulation
scenarios compared to the other nonlinear filtering
algorithms considered here. The steady state values
of the RMS errors provided by the proposed
algorithm are also found to be less compared to the
other considered adaptive and non adaptive
nonlinear filtering algorithms.
4 CONCLUSIONS
The problem of nonlinear state estimation at the
presence of non-additive measurement noise with
unknown noise covariance has been considered here.
Towards the solution of the above stated problem an
Adaptive Unscented Kalman Filter (AUKF) has
been proposed which utilizes the augmented form of
state vector. It has been found from the total corpus
of simulation results that the proposed adaptive filter
provides less RMS errors and is more robust to the
initial uncertainties associated with the measurement
0
0.2
0.4
0.6
0.8
1
1.2
0 5 10 15 20
Tim e (se c.)
RMSE of velocity (m/sec.)
UKF
Augmented AUKF
AUKF w ith additive noise
ADDF
0
2
4
6
8
10
12
14
16
18
Track
losses
Augmented
AUKF
AUKF w ith
additive
noise
UKF A DDF
0
20
40
60
80
100
120
140
160
0 5 10 15 20
Time (sec.)
RMSE of Position (m)
UKF
Augmented AUKF
AUKF w ith additive noise
A DDF
0
1
2
3
4
5
6
7
0 5 10 15 20
Tim e (sec.)
RMSE of velocity (m/sec.)
UKF
Augmented AUKF
AUKF w ith additive noise
ADDF
0
10
20
30
40
50
60
Track
losses
Augmented
AUKF
AUKF w ith
additive
noise
UKF A DDF
AdaptiveUnscentedKalmanFilteratthePresenceofNon-additiveMeasurementNoise
619

noise covariance (R) compared to few selected
existing adaptive and non-adaptive filtering
techniques. Probability of failure in the proposed
filtering technique has also been observed to be
negligible compared to the other filtering techniques
involved. The results provided in this paper to
demonstrate the superiority of the proposed adaptive
filter are expected to encourage further studies on
Adaptive Unscented Kalman Filtering techniques for
non-additive noise.
ACKNOWLEDGEMENTS
The first two authors would like to thank the Council
of Scientific and Industrial Research, India, for
financial support.
REFERENCES
Almagbile, A., Jinling, W., Weidong, D., 2010. Evaluating
the performances of adaptive Kalman filter methods in
GPS/INS integration. In Journal of Global Positioning
Systems
, 9(1), 33-40.
Mehra, R., 1972. Approaches to adaptive filtering. In
IEEE Transaction on Automatic Control, 17(5), 693-
698.
Busse, F. D., How, J., Simpson, J., 2003. Demonstration
of adaptive extended Kalman filter for low earth orbit
formation estimation using CDGPS. In Journal of the
Insitute of. Navigation, 50(2), 79-93.
Meng, Q., Sun, Y., Cao, Z., 2000. Adaptive extended
Kalman filter (AEKF)-based mobile robot localization
using sonar. In
Robotica, 18(5), 459-473.
Wan, E. A., Van Der Merwe, R., 2000. The unscented
Kalman filter for nonlinear estimation. In
Proceedings
of IEEE Symposium (AS-SPCC)
, Lake Louise, Alberta,
Canada, 153-158.
Fathabadi, V., Shahbazian, M., Salahshour, K., Lotfollah,
J., 2009. Comparison of adaptive Kalman filter
methods in state estimation of a nonlinear system
using asynchronous measurements. In
Proceedings of
the World Congress on Engineering and Computer
Science
, 2, San Francisco, USA.
Das, M., Sadhu, S., Ghoshal, T. K., 2013. An adaptive
sigma point filter for nonlinear filtering problems. In
International Journal of Electrical Electronics and
Computer Engineering
, 2(2), 13-19.
Das, M., Sadhu, S., Ghoshal, T. K., 2014. Spacecraft
attitude & rate estimation by an adaptive unscented
Kalman filter. In
International Conference on Control,
Instrumentation, Energy and Communication (CIEC)
.
Soken, H. E., Hajiyev, C., 2011. A novel adaptive
unscented Kalman filter for pico satellite attitude
estimation. In
PHYSCON, Leon, Spain.
Chai, W., Chen, C., Ezzaldeen, E., Zhang, J., Loffeld, O.,
2012. INS/Wi-Fi based indoor navigation using
adaptive Kalman filtering and vehicle constraints. In
9th Workshop on Positioning, Navigation and
Communication
, Dresden, Germany, 36-41.
Das, M., Dey, A., Sadhu, S., Ghoshal, T. K., 2015.
Adaptive central difference filter for non-linear state
estimation. In
IET Science, Measurement &
Technology
, 1-6.
Dey, A., Sadhu, S., Ghoshal, T. K., 2015. Adaptive
divided difference filter for nonlinear systems with
non-additive noise. In
Third International Conference
on Computer, Communication, Control and
Information Technology (C3IT)
.
Norgaard, M., Poulsen, N. K., Ravn, O., 2000. New
developments in state estimation for nonlinear
systems. In
Automatica, 36(11), 1627-1638.
Ito, K., Xiong, K., 2000. Gaussian filters for nonlinear
filtering problems. In IEEE Transactions on Automatic
Control
, 45 (5), 910-927.
Mohamed, A. H., Schwarz, K. P., 1999. Adaptive Kalman
filtering for INS/GPS. In Journal of Geodesy, 73(4),
193-203.
Sadhu, S., Mondal, S., Srinivasan, M., Ghoshal, T. K.,
2006. Sigma point Kalman filter for bearing only
tracking. In Signal processing, 86(12), 3769-3777.
Lin, X., Kirubarajan, T., Bar-Shalom, Y., Maskell, S.,
2002. Comparison of EKF, pseudomeasurement filter
and particle filter for a bearing-only tracking problem.
In Proceedings of the SPIE Conference of Signal and
Data Processing of Small Targets
, Orlando, FL.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
620