High Precision Temperature Control of Normal-conducting RF GUN for

a High Duty Cycle Free-Electron Laser

Kai Kruppa

, Sven Pfeiffer

, Gerwald Lichtenberg

, Frank Brinker

, Winfried Decking

Klaus Fl

ottmann

, Olaf Krebs

, Holger Schlarb

and Siegfried Schreiber

Faculty of Life Sciences, Hamburg University of Applied Sciences, Ulmenliet 20, 21033 Hamburg, Germany

Deutsches Elektronen Synchrotron DESY, 22607 Hamburg, Germany

Keywords:

Nonlinear Systems, Thermal Modelling, Predictive Control, RF Cavities.

Abstract:

High precision temperature control of the RF GUN is necessary to optimally accelerate thousands of electrons

within the injection part of the European X-ray free-electron laser XFEL and the Free Electron Laser FLASH.

A difference of the RF GUN temperature from the reference value of only 0.01 K leads to detuning of the

cavity and thus limits the performance of the whole facility. Especially in steady-state operation there are

some undesired temperature oscillations when using classical standard control techniques like PID control.

That is why a model based approach is applied here to design the RF GUN temperature controller for the

free-electron lasers.

A thermal model of the RF GUN and the cooling facility is derived based on heat balances, considering the

heat dissipation of the Low-Level RF power. This results in a nonlinear model of the plant. The parameters are

identiﬁed by ﬁtting the model to data of temperature, pressure and control signal measurements of the FLASH

facility, a pilot test facility for the European XFEL. The derived model is used for controller design. A linear

model predictive controller was implemented in MATLAB/Simulink and tuned to stabilize the temperature of

the RF GUN in steady-state operation. A test of the controller in simulation shows promising results.

1 INTRODUCTION

This paper deals with temperature control of the

radio-frequency (RF) GUN for the European X-Ray

free-electron laser XFEL at the Deutsches Elektronen

Synchrotron (DESY). The 1.15 billion Euro XFEL fa-

cility with a length of 3.4 kilometers is under con-

struction, (Altarelli et al., 2006). With European

XFEL it will be possible to generate intense X-

ray laser pulses with a few femtosecond duration.

The electrons are accelerated by 101 superconducting

modules and forced through an undulator leading to

a sinusoidal path and therefore to the release of pho-

tons, i.e. synchrotron radiation. This narrow band-

width photon beam with wavelength down to 0.05 nm

allows to take 3D images at the atomic level. Figure 1

shows the XFEL tunnel with accelerator modules.

Simulation methods allow to develop algorithms

and model-based feedback schemes even before the

European XFEL is in operation. The approaches can

be veriﬁed and tested by parameters taken from the

Free Electron Laser FLASH, which is the ﬁrst soft

Figure 1: Tunnel of European XFEL (Source: DESY).

X-ray facility ever build and nowadays used for pho-

ton science, (FLASH, 2013). Even though FLASH is

a smaller facility with a length of 315 meters, it has

a comparable structure. The modelling and parame-

ter identiﬁcation here is done with data from FLASH.

With parameter adjustments this model should be

used at XFEL, too. This allows to derive control

structures for optimal performance of FLASH and the

new XFEL even before its operation starts.

307

Kruppa K., Pfeiffer S., Lichtenberg G., Brinker F., Decking W., Flöttmann K., Krebs O., Schlarb H. and Schreiber S..

High Precision Temperature Control of Normal-conducting RF GUN for a High Duty Cycle Free-Electron Laser.

DOI: 10.5220/0005567503070317

In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),

pages 307-317

ISBN: 978-989-758-120-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

The RF GUN is the electron source of the whole fa-

cility, (Hoffmann et al., 2015). Temperature control

is a very important task in RF GUN operation be-

cause a temperature that does not ﬁt the reference

value leads to detuning of the cavity. This limits the

performance of the RF GUN such that it cannot be

operated optimally. A ﬁrst investigation of a model

based controller approach for steady-state operation

of the RF GUN as example at FLASH is investigated

here. Therefore a thermal model of the RF GUN and

its water cooling circuit is derived respecting the in-

ﬂuence of the dissipated power of the low-level radio

frequency control structures (LLRF). Parameters are

identiﬁed by ﬁtting the model to measurement data.

Moreover simulations of the model can be used inter-

nally inside a model predictive controller (MPC) to

get optimal signals for RF GUN temperature control.

A linear MPC approach shows promising results in

simulation.

The paper is organized as follows. In Section 2

the system with cooling circuit and RF GUN with its

sensors and actors is described ﬁrst. Afterwards in

Section 3 a dynamical nonlinear model of the plant

is developed and the parameters are estimated based

on measurement data in Section 4. This model is

used to design a model predictive controller in Sec-

tion 5 which is implemented in MATLAB/Simulink

and tested in simulation. Summary and options for

future work are given in Section 6.

2 PLANT

This section introduces the main characteristics of the

plant that should be modelled. The data and struc-

ture of the FLASH facility will be used here to derive

the model. The XFEL RF GUN will be similar to

FLASH gun such that the basic structure of the model

can be applied to XFEL, too. Therefore the setup

and the location of important sensors are described.

The electron source of the free electron laser is the

RF GUN. Electrons are extracted from the cathode

and accelerated by an electric ﬁeld. The microwave

power, necessary to accelerate the electrons, is gen-

erated by a klystron and is coupled over a waveguide

to the gun. The cavity is operated at a resonance fre-

quency of 1.3 GHz. It is very important that the cavity

works under tuned conditions at resonance frequency

to get an efﬁcient acceleration of the electrons. The

gun body is build of copper and has a structure of a

hollow cylinder with 1.5 cells. Because of dissipated

RF power the RF GUN heats up such that a cool-

ing is necessary to control the temperature of the gun

body and to operate the RF GUN under tuned con-

ditions. The average cooling load is in the order of

several 10 kW. A schematic cross-section of the RF

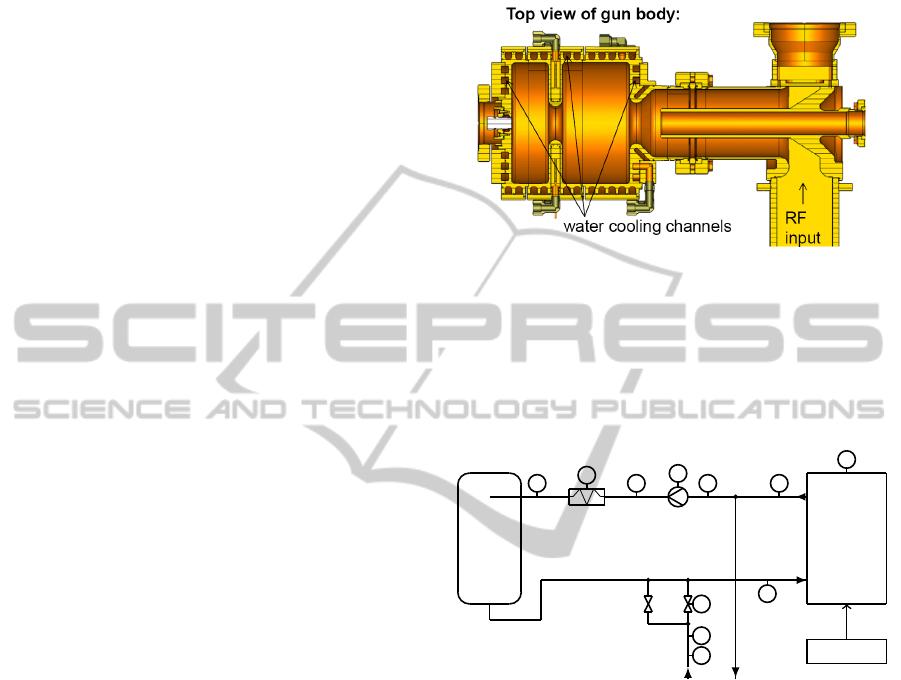
GUN at FLASH is depicted in Figure 2.

Figure 2: RF GUN at FLASH, (Stephan, 2015).

The system focused here at FLASH consists of the

RF GUN controlled by LLRF and the water circuit

which supplies the RF GUN with cooling water. Fig-

ure 3 shows the schematic setup.

Tank

RF GUN

LLRF

Inﬂow Outﬂow

Figure 3: RF GUN with cooling circuit, existing tempera-

ture sensors T , pressure sensors p and control inputs α.

The RF GUN is equipped with cooling pipes to

control its temperature. They are supplied with cold

water. In typical operation (T

> T

) warmer water

leaves the RF GUN, because the RF GUN heats up

due to RF power losses. The water circuit supplying

the RF GUN consists of a heater, a water tank, mixing

valves and a water inlet and outlet. The mixing valves

allow to add cold water of a water reservoir from the

inﬂow to the water circuit to cool the water down. The

inﬂow is controlled by two valves, a small and a big

one. Most of the time the big valve is closed such that

the whole ﬂow is controlled by the small one. On the

other side of the RF GUN water of the same amount

is taken out at the water outﬂow. The volume ﬂow

in the circuit is controlled by a pump. If necessary,

a heater is available to heat up the water in the cir-

cuit. The heater keeps the temperature constant if the

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

308

RF GUN is not in operation, such that the water does

not cool down to room temperature. A water tank is

installed between the heater and the mixing valves.

With this tank possible temperature oscillations in the

circuit should be damped such that a disturbance in

the water temperature is not fed back directly to the

RF GUN. The tank acts like a low-pass ﬁlter.

The cooling water circuit and the RF GUN are pro-

vided with several temperature and pressure sensors.

All temperature sensors are PT100 sensors with four

wire connection. Five temperature sensors T

and T

to T

are located in the water circuit outside the

RF GUN. The pressure is measured at two loca-

tions p

and p

. The locations of the sensors are

depicted in Figure 3. Additionally the control inputs

of the pump α

, the valves α

and the heater α

are

recorded. Five further sensors measure the tempera-

ture inside the RF GUN. The rough position of these

sensors in red and the cooling pipes in blue are high-

lighted in Figure 4.

iris

cell1

cell2

cell3

coupler

Figure 4: Gun body with sensors.

Three sensors are located near the outside surface

of the RF GUN such that they are inﬂuenced much by

the cooling water. One sensor is at the iris and one

sensor at the coupler tube, which is the connection of

the RF GUN to the next acceleration modules. The

iris sensor T

is the most representable sensor for the

temperature inside the RF GUN.

3 THERMAL MODEL OF THE

PLANT

In this section the model of the RF GUN and the

cooling circuit is derived. A grey-box modelling ap-

proach is used here. Only the effects that inﬂuence

the dynamics the most should be considered here. All

other minor effects are neglected because they have

just a small inﬂuence on the dynamical behaviour of

the component. This leads to models that are not too

complicated and do not need too much computational

effort in simulation. This makes them suitable for

controller design.

The basis of all following modelling approaches

are heat balances. This means that the sum of sup-

plied power

in,i

and discharged power

out, j

should

be equal to the stored power

stored

in the component.

The supplied power contributes with a positive sign

and the discharged power with a negative sign to this

balance

stored

∑

in,i

−

∑

out, j

. (1)

The heat is given by, (Kuchling, 1991)

Q = cρV T, (2)

where c is the speciﬁc heat capacity, ρ the density, V

the volume and T the temperature of the medium.

The thermal behaviour of the RF GUN should be

modelled taking into account the inﬂuence of LLRF

control structures. Operating the RF GUN at a certain

acceleration gradient requires RF power controlled by

LLRF system. The RF GUN is heated by RF power

loss caused by normal conducting resonator. From

the RF point of view it is necessary to have a certain

gun temperature to operate under tuned conditions.

If there are temperature deviations the cavity is de-

tuned. It is still operable but works under suboptimal

conditions, e.g. increase in RF power to achieve the

nominal accelerating gradient. Therefore the cavity

requires additional RF power in this case.

3.1 Cooling Pipes

The RF GUN must be cooled to control its temper-

ature. This is done by cooling pipes that are dis-

tributed in the whole RF GUN body. The cooling

pipes schematically indicated in blue in Figure 4 are

supplied with cold water from the water circuit with

temperature T

and ﬂow

. As simpliﬁcation it is as-

sumed that the water in the pipes is completely mixed

with temperature T

and no ﬂow losses occur. The wa-

ter leaves the pipes of RF GUN with temperature T

and ﬂow

. Since the pipes cool the RF GUN a heat

transfer between cooling pipes and gun body takes

place that is proportional to the difference of the tem-

peratures of RF GUN and cooling water with a fac-

tor k

. A small part of the power gets lost to the envi-

ronment. The environmental temperature is assumed

to be constant, because the inﬂuence of variations of

this temperature on the behaviour of the RF GUN is

negligible. It is represented by a constant parame-

ter T

env

. These losses are modelled by a heat transfer

proportional to the difference between the tempera-

tures of the pipe and the environment with constant

HighPrecisionTemperatureControlofNormal-conductingRFGUNforaHighDutyCycleFree-ElectronLaser

309

of proportionality k

. The balance of all the powers

gives

= c

− T

) − k

− T

env

)

−k

−T

), (3)

where V

is the volume of the cooling pipes and c

and ρ

the speciﬁc heat capacity and density of water.

Rearranging (3) gives a ﬁrst order differential equa-

tion to compute the return temperature T

of the cool-

ing pipes

− T

) −

− T

env

)

−

− T

). (4)

3.2 Gun Body

The temperatures of the gun body are measured by

ﬁve sensors. The temperature distribution inside the

RF GUN depends on the electromagnetic ﬁeld and is

very complicated, (Fl

ottmann et al., 2008). The fo-

cus of the model developed here is its applicability

for controller design which leads to the negligence of

these complex effects.

Because of this the RF GUN is modelled as one body

with one temperature T

representing the thermal be-

haviour of the whole RF GUN. One of the ﬁve sensors

should be representable for the RF GUN. The three

sensors T

cell,i

, i = 1, 2, 3 at the outer surface of the RF

GUN are very much inﬂuenced by the cooling pipes

and do not show the inﬂuence of the LLRF properly.

The sensor T

coupler

at the RF GUN exit measures in-

ﬂuences from the coupling too. That is why the sensor

next to the iris was chosen T

= T

iris

. It is located next

to the middle of the gun body and is inﬂuenced by the

LLRF as well as by the cooling circuit.

The energy balance of the gun body contains three

parts. The heat transfer from the cooling pipes is pro-

portional to the temperature difference of T

and T

with the factor k

as in (3). The RF GUN has losses

to the environment with temperature T

env

. The heat

transfer coefﬁcient is k

. The third part of the bal-

ance is the dissipated power P

diss

of the LLRF. The

powers sum up to

diss

−T

)−k

−T

env

), (5)

which gives the differential equation of the gun tem-

perature

diss

− T

)

−

− T

env

). (6)

The volume of the RF GUN is denoted by V

and it is

assumed that it is fully build of copper with material

constants c

and ρ

. The computation of the dissi-

pated power is described in the next part.

3.3 Thermal Inﬂuence of the LLRF

The RF GUN is heated by the thermal losses of the

LLRF power. The cavity voltage depends on the input

power and detuning, i.e. correlated to the RF GUN

temperature. If the temperature of the RF GUN devi-

ates from its optimal setpoint, the cavity gets detuned

which leads to an increase of reﬂected power in the

cavity and with that the cavity voltage decreases by

destructive interference of forward and reﬂected sig-

nal. The following model describes this behaviour of

the RF and its thermal effects. The modelling of the

RF inside the cavity and its dissipated power are based

on (Schilcher, 1998).

If the cavity is supplied by forward power there ex-

ists an electric ﬁeld inside the cavity. Integration of

the electric ﬁeld gives the cavity voltage V

cav

. The

real part of this voltage accelerates the electrons in the

cavity. But the RF ﬁeld also induces a certain surface

current at the wall of the cavity which heats up the de-

vice. The RF behaviour of the cavity can be modelled

by an LCR resonator circuit, shown in Figure 5.

ext

Figure 5: LCR resonator circuit.

The resistance represents the losses that are trans-

ferred to the gun body as heat

diss

cav

. (7)

The shunt resistance R

is deﬁned as two times the

cavity resistance 2R. The loaded shunt impedance R

in the LCR circuit is the parallel connection of the

cavity resistance and the external load Z

ext

With the electrical equivalent circuit the cavity volt-

age is given by a second order differential equation

cav

I, (8)

cav

+ ω

cav

I, (9)

with the resonance frequency ω

and the loaded qual-

ity factor Q

. The circuit is excited by the forward

current I coming from the klystron. The stationary

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

310

solution of (9) with harmonic excitation I =

sin(ωt)

gives

cav

sin(ωt + ψ), (10)

with the amplitude

cav

and the angular frequency ω

of the cavity voltage and the detuning angle ψ. The

angle ψ describes the difference between forward

phase and the phase of the cavity voltage

ψ = φ

f or

− φ

cav

. (11)

Under tuned, which means optimal resonance oper-

ating conditions, the phase is equal to the phase of

the cavity voltage φ

f or

= φ

cav

such that the detun-

ing ψ is equal to zero. For small frequency devia-

tions ∆ω = ω

− ω  ω

the detuning and the ampli-

tude variations are given by

tan(ψ) ≈ 2Q

∆ω

, (12)

cav

≈

1 + tan(ψ)

. (13)

Equation (13) describes the behaviour of the ampli-

tude of the cavity voltage depending on the detun-

ing

cav

(ψ). Since the forward current is not available

as measurement but the forward power P

f or

= R

f or

(14)

has to be inserted in (13) to make it usable for a pa-

rameter estimation

cav

≈

f or

1 + tan(ψ)

. (15)

The detuning ψ depends on the temperature of the RF

GUN. A change in gun temperature ∆T

leads to a

change in geometry of the RF GUN. The inﬂuence

of the temperature change on the detuning can be de-

scribed by a constant factor α such that the tempera-

ture change is assumed to be proportional to the tan-

gent of the detuning

tan(ψ) = α∆T

, (16)

with proportional constant α. It is assumed that the

setpoint T

g,SP

of the gun temperature is always chosen

optimal such that the detuning is zero if T

is equal

to T

g,SP

∆T

= T

− T

g,SP

= 0 ⇔ T

= T

g,SP

→ ψ = 0. (17)

Inserting to (16) gives

tan(ψ) = α(T

− T

g,SP

). (18)

The constant α can be estimated from measurement

data by a linear approximation of the relation between

detuning tan(ψ) and gun temperature. The temper-

ature dependence of the cavity voltage can be com-

puted by inserting (18) into (15) resulting in

cav

) =

f or

1 + α

− T

g,SP

)

. (19)

Figure 6 shows the temperature dependence of

cav

with a chosen value of α = −26

. During parameter

estimation this turned out to be a typical value for α.

Figure 6: Temperature dependence of the cavity voltage.

3.4 Cooling Circuit

The cooling water circuit supplies the RF GUN with

cold water. The model of the circuit is divided into

three parts, as depicted in Figure 7. The borders be-

tween the different parts are set according to the posi-

tions of the temperature sensors T

, . . . , T

Tank

Figure 7: Scheme of the cool water circuit with partitioning

for modelling.

The ﬁrst part of the cooling circuit starts at the

water outlet of the cooling pipes of the RF GUN. The

water leaves the RF GUN with the ﬂow

. Its temper-

ature is measured by the sensor T

. Since no power is

added or removed the temperature T

can be modelled

by a simple time delay

HighPrecisionTemperatureControlofNormal-conductingRFGUNforaHighDutyCycleFree-ElectronLaser

311

(t) = T

(t − T

d,21

). (20)

It takes some time since the water from T

reaches

the second sensor position T

. Temperature losses in

the pipes are neglected. The ﬂow

is split up. The

ﬂow

is fed back to the water reservoir. The re-

maining part

−

(21)

ﬂows through the water circuit.

In part 2 the temperature is mainly inﬂuenced

by an electrical heater that heats the water ﬂowing

through the device. The added power

can be con-

trolled linearly by its control input α

∈ [0, 1] resulting

= α

h,max

, (22)

with

h,max

denoting the maximum power of the

heater. The heater used here has a speciﬁed maxi-

mum power of 6 kW . Water with the temperature T

enters the heater with a ﬂow

. Warm water with

temperature T

leaves the component with the same

ﬂow. Building the thermal balance gives

(t) = c

((T

(t) − T

(t−T

d,32

))

(t), (23)

where V

is the volume of the heater. Rearrang-

ing (23) and inserting (22) gives the differential equa-

tion for T

(t) =

(t) − T

(t−T

d,32

))

h,max

(t). (24)

There is a time delay in this part of system, denoted

by the parameter T

d,32

The water circulates in the pipes because of the pump.

It sets up the volume ﬂow

. The pump is controlled

by the signal α

∈ [0, 1]. Since no volume ﬂow rate

measurements are available in the whole cooling cir-

cuit it is hard to model the pump and the volume ﬂow.

Thus a linear dependence between the volume ﬂow

and the control input of the pump is assumed by

= α

k,max

, (25)

with maximal possible ﬂow

k,max

for α

= 1. The

maximal volume ﬂow

k,max

is a parameter that will

be determined during parameter estimation. This sim-

ple model can be used because the focus of the overall

model is on steady-state operation. Under this condi-

tion the volume ﬂow and the control signal just vary

a little which justiﬁes a linear approximation of the

nonlinear behaviour of the pump around an operating

point.

The third part of the cooling circuit contains the

most important devices. The water ﬂows through the

tank to damp most of the ﬂuctuations in the tempera-

ture. Behind the tank, water from a cold water reser-

voir is added by a mixing valve to cool the water. The

measurement information that is available here are the

temperatures T

and T

of the inﬂowing and outﬂow-

ing water of the cooling circuit, the temperature T

of the inﬂowing cold water, the valve position α

and

the pressure on the reservoir side of the valve.

Since the tank should damp the temperature ﬂuctua-

tions in the circuit a simple model of a low-pass is

used here. The output temperature of the tank is un-

known. Water with temperature T

enters with the

ﬂow

. The unknown output temperature of the tank

with volume V

is denoted by T

. The thermal balance

of the tank gives

= c

− c

(26)

⇔

− T

). (27)

The water leaving the tank is mixed with the cold

water from a reservoir with temperature T

. The

ﬂow

is not captured by a sensor. Only estima-

tions are possible. The ﬂow is inﬂuenced by the valve

position α

. A ﬁrst modelling approach is a linear de-

pendence of the ﬂow through the valve from the valve

position

cw,max

, (28)

with the maximal ﬂow

cw,max

that should be identi-

ﬁed by a parameter estimation. Since the valve does

not react instantaneously on a change in the control

signal α

, the reaction of the valve is modeled in

Laplace domain (denoted by s) by a linear damping

of the control signal resulting in

(s) =

s + 1

(s). (29)

The mixed ﬂow that supplies the RF GUN is de-

scribed by

, (30)

. (31)

Combining the three parts gives the model of the over-

all cooling circuit.

3.5 Overall Model

Equations (4), (6), (7) and (19) describing the thermal

behaviour of the RF GUN and equations (20) to (31)

describing the dynamics of the cooling circuit form

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

312

the thermal model of the overall plant. This results in

a nonlinear, multiple input, multiple output (MIMO)

state space model

x = f(x, u), (32)

y = g(x, u), (33)

with six inputs

u =



g,SP

f or



, (34)

ﬁve states

x =





, (35)

and the parameters to be identiﬁed



α R

···

d,21

d,32

k,max

cw,max

h,max

env



The derived MIMO model describes the thermal be-

haviour of the RF GUN facility taking into account

the inﬂuence of the water cooling and the LLRF on

the gun body. The cross couplings of the cooling and

the LLRF power can be simulated by having the con-

trol signals of the water circuits α

, α

and the for-

ward power P

f or

of LLRF as inputs to the plant. The

whole model was implemented and simulated using

MATLAB/Simulink, (Mathworks, 2014b).

4 PARAMETER ESTIMATION

The data available for estimation and validation are

recorded with a sampling rate of approximately one

second at FLASH. From an LLRF point of view no in-

trapulse information are used. The model works with

average powers. The LLRF signal inﬂuencing the gun

temperature here is the forward power P

f or

. Its peak

values P

f or,peak

are measured by a power meter. The

average power follows from

f or

= P

f or,peak

τ f

rep

, (36)

with a ﬂattop time τ and a pulse repetition rate f

rep

of 10 Hz. With this data the parameters of all parts

of the model are estimated componentwise ﬁrst. This

means that the parameters of each component on its

own are adapted to its input/output measurement data.

All parts are fed with measured input data and the

parameters are changed such that the quadratic dif-

ference between simulated and measured outputs is

minimized, (Ljung, 1987). The estimated parameters

were cross-validated by a second different data set.

The parameter estimations were done by the Simulink

Design Optimization Toolbox of MATLAB, (Math-

works, 2014a).

4.1 Componentwise Estimation

The parameters of the RF GUN are identiﬁed by feed-

ing the inputs T

, T

g,SP

and P

f or

with measure-

ment data and identify the parameters such that the

simulated output signals T

and T

are ﬁt to the cor-

responding measured values. A simulation of the RF

GUN with the resulting parameters and the validation

data set shows the results of the parameter estimation

of the RF GUN, depicted in Figure 8. Figure 9 shows

a zoom in time range of the simulation results. The

model captures the dynamics of the RF GUN very

well except of a certain offset.

0 200 400 600 800 1000

61.1

61.2

61.3

Temperature [°C]

Measurement T

Simulation T

Setpoint

0 200 400 600 800 1000

55.5

55.6

55.7

55.8

Time [min]

Temperature [°C]

Measurement

Simulation

Figure 8: Validation results of the gun model.

740 750 760 770 780 790 800

61.1

61.2

61.3

Temperature [°C]

Measurement T

Simulation T

Setpoint

740 750 760 770 780 790 800

55.5

55.6

55.7

55.8

Time [min]

Temperature [°C]

Measurement

Simulation

Figure 9: Validation results of the gun model (Zoom).

The parameters of the water circuit were identiﬁed

with the input signals T

, T

, α

and α

together

with the output temperatures T

, T

and T

. The re-

sults of the validation simulation are depicted in Fig-

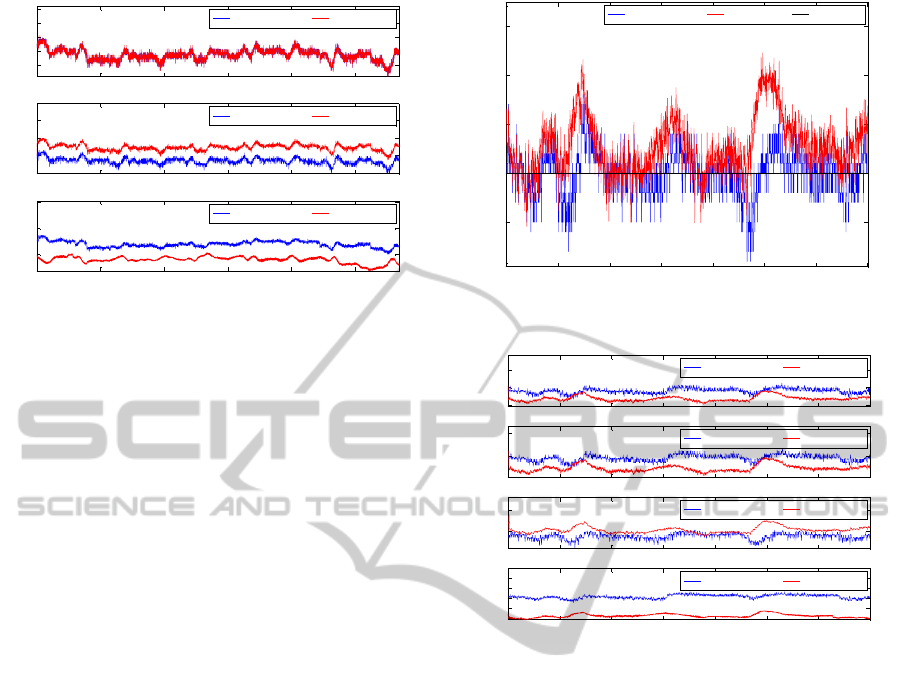
ure 10.

The simulation shows that the behaviour at sen-

sor position 2 and 3 are captured well. The model

shows the same dynamics. The temperature T

only

shows an offset. The difference between measure-

ment and simulation of temperature T

is much larger.

HighPrecisionTemperatureControlofNormal-conductingRFGUNforaHighDutyCycleFree-ElectronLaser

313

0 200 400 600 800 1000

55.5

55.6

55.7

55.8

55.9

Temperature [°C]

Measurement T

Simulation

0 200 400 600 800 1000

55.8

56.2

56.4

Temperature [°C]

Measurement T

Simulation

0 200 400 600 800 1000

52.5

Time [min]

Temperature [°C]

Measurement T

Simulation

Figure 10: Validation results of the cooling circuit model.

The model does not show all the dynamics of the real

system. A reason for this modelling error could be

that only few measurement information is available

in this part of the system. The behaviour of the tank

and the mixing valve are captured together by the sen-

sor T

. This makes it hard to model these components,

because their effects cannot be measured separately.

The missing ﬂow information contributes to the error,

too.

4.2 Overall Estimation

After this componentwise estimation of the model pa-

rameters, the different parts of the model are linked to

the overall model as shown in Section 3.5. This closes

the water circuit. The return water of the RF GUN is

linked as input to the water circuit which cools the

water down and supplies the gun pipes with cold wa-

ter. With this model a ﬁne tuning of the parameters

was done. The results of the simulation with valida-

tion data of the RF GUN and the cooling circuit are

shown in the following Figures 11 and 12.

These simulations show that the dynamics of the

gun temperature in the closed circuit cannot be cap-

tured as good as before in the componentwise simula-

tion. These differences can be explained by the mod-

elling errors in the last part of the cooling circuit. The

modelling errors occurring in this part are fed back to

the RF GUN resulting in a propagation of the error.

The simulated gun temperature shows an additional

offset, but the main dynamics of the RF GUN are still

captured.

The reasons for the modeling errors could be the

missing ﬂow information. There are no ﬂow sensors

provided even though the ﬂow is a very important

item of the model, because it deﬁnes the heat power.

Flow estimations are very rough. Additionally it is

assumed that one temperature sensor represents the

whole RF GUN which cannot model the behavior ex-

0 50 100 150 200 250 300 350

61.05

61.1

61.15

61.2

Time [min]

Temperature [°C]

Measurement T

Simulation T

Setpoint

Figure 11: Validation results of the overall model (Gun tem-

perature).

0 50 100 150 200 250 300

55.4

55.6

55.8

Temp. [°C]

Measurement T

Simulation

0 50 100 150 200 250 300

55.6

55.8

Temp. [°C]

Measurement T

Simulation

0 50 100 150 200 250 300

56.2

Temp. [°C]

Measurement T

Simulation

0 50 100 150 200 250 300

51.8

52.2

52.4

52.6

Time [min]

Temp. [°C]

Measurement T

Simulation

Figure 12: Validation results of the overall model (Circuit

temperatures).

actly. But it should be sufﬁcient for controller design.

5 MODEL PREDICTIVE

CONTROL

In this part the model of FLASH derived in Section 3

is used to design a model predictive controller (MPC).

At each sampling instant the controller computes the

optimal future control input with respect to a certain

cost function such that e.g. the system follows a given

trajectory. A linear MPC approach is used here. This

means that ﬁrst of all the model of Section 3 has to be

linearized around a given operating point. After that

the linear MPC can be designed and tuned.

5.1 Control Problem

The theory of linear MPC with constraints will now

be applied in simulation to control the temperature of

the gun, (Maciejowski, 2002). As ﬁrst controller ap-

proach for the facility a controller for a SISO mod-

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

314

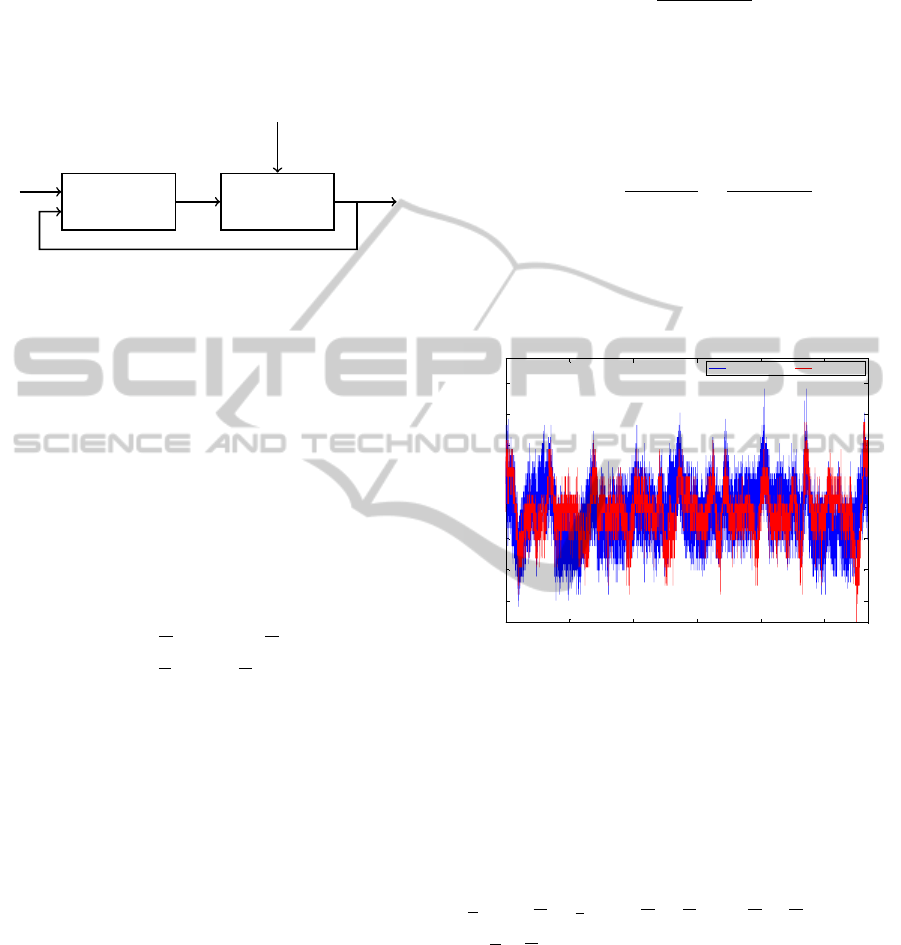
elled plant is depicted here. The controller should set

the position of the valve α

such that the difference

between gun temperature T

and its set point T

g,SP

minimal. The system is disturbed by the cold water

with temperature T

and the environment tempera-

ture T

env

. Figure 13 shows the structure of the design.

Predictive

controller

System

env

g,SP

Figure 13: Controller structure.

Inside the controller a linearization of the nonlin-

ear plant model is used to simulate system responses

to different input signals. With that an optimal control

signal for the plant can be computed. Thus ﬁrst of all

a linear, single input, single output (SISO) model of

the nonlinear MIMO model is derived. The controller

should stabilize the temperature in steady-state oper-

ation. This justiﬁes the use of a linear model. It is

valid for a certain range around the operating point.

For start up operation of the gun this linear model is

probably not suitable. But for steady-state operations

it ﬁts the needs. Because of that some inputs of the

nonlinear model are set to constants to linearize it

g,SP

= T

g,SP

, T

= T

, (37)

= α

, α

= α

(38)

The overline indicates the operating point of the cor-

responding inputs. This does not limit the perfor-

mance of the model, because the dynamics of the sig-

nals does not inﬂuence the dynamics of the model ex-

tremely. The cold water temperature inﬂuences the

model, but it is hard to estimate the behaviour of this

temperature. As ﬁrst assumption it is set constant

here. The forward power has an enormous inﬂuence

on the dynamics of the gun temperature. The model

in the controller estimates the future states of the gun.

Since these states depend on the forward power an es-

timation of the future forward power has to be found.

Because of that the inﬂuence of the LLRF con-

trol on the forward power has to be modelled some-

how. The LLRF control tries to keep the cavity volt-

age constant. The cavity voltage decreases if the cav-

ity is detuned. If e.g. the voltage decreases the for-

ward power is increased to compensate the voltage

decrease in the cavity. The inﬂuence of the detuning

on V

cav

was modelled by (15). With the assumption of

a constant cavity voltage a relation between forward

power and detuning can be found resulting in

f or

= C

1 + tan

(ψ)

(39)

with an unknown constant factor C.

The dynamic behaviour of the relation should be ap-

proximated by a linear model. A black box identiﬁ-

cation with the System Identiﬁcation Toolbox gives a

ﬁrst order transfer function model, (Ljung, 2001)

LLRF

(s) =

LLRF

(s)

LLRF

(s)

LLRF

s + 1

(40)

with the input U

LLRF

(s) = α(T

− T

g,SP

) and the out-

put Y

LLRF

(s) = P

f or

. The simulation results of the val-

idation of the LLRF model are shown in Figure 14

with K

LLRF

= −56 and T

LLRF

= 0.8.

0 200 400 600 800 1000

2.175

2.18

2.185

2.19

2.195

2.2

2.205

2.21

x 10

Time [min]

Power [W]

Measurement Simulation

Figure 14: Linear approximation of the forward power P

f or

This LLRF model is linked to the plant model of

Section 3.5 to generate the forward power P

f or

. Since

the ﬁrst order approximation of the LLRF control is

only very rough, this introduces an additional mod-

elling error, but it should be sufﬁcient for the ﬁrst

controller approach here. With the assumptions (37)

and (38) this allows us to linearize the nonlinear

model around the operation point

gun



LLRF

v, f ilt



, (41)

u = α

, (42)

to get a linear model with 6 states, one input u

gun

= α

and one output y

gun

= T

gun

= A

gun

+ B

gun

, (43)

gun

= C

gun

+ D

gun

. (44)

The state x

LLRF

is the state introduced by the linear

approximation (40) of the behaviour of the LLRF con-

trol. The simulation results of the SISO model and its

linearization are shown in Figure 15 compared to the

HighPrecisionTemperatureControlofNormal-conductingRFGUNforaHighDutyCycleFree-ElectronLaser

315

measurement data and the MIMO model. The simula-

tion shows that the approximation of the LLRF con-

trol by a linear model (40) adds an offset error. An

improvement of the LLRF model could reduce this er-

ror. The fast variations of the gun temperature are not

captured as good as before as well. Linearizing this

model introduces just a small additional error. Be-

cause of that it is possible to use the linear model (43)

and (44) for control.

0 200 400 600 800 1000 1200

60.9

61.1

61.2

61.3

61.4

61.5

61.6

Time [min]

Temperature [°C]

Measurement

Sim.

Sim. with LLRF model

Linearization

Figure 15: Simulation results of the model without and with

LLRF approximation and its linearization.

The theory of MPC is used here according

to, (Maciejowski, 2002) meaning that the linear SISO

model is used by the MP controller to compute opti-

mal input sequences to the plant according to the cost

function

J(k) =

∑

i=1

gun

(k + i) − r

gun

(k + i)k

Q(i)

∑

i=1

k∆u

gun

(k + i)k

R(i)

, (45)

where ∆u

gun

(k + i) = u

gun

(k + i) − u

gun

(k + i − 1) are

the input changes and r

gun

(k + i) ∈ R

n×1

the state

reference. This means that the states should fol-

low a reference trajectory r

gun

with a certain con-

trol effort ∆u

gun

. The differences of the states

from the reference are weighted by the positive

semi-deﬁnite matrices Q(i) ≥ 0 ∈ R

n×n

and the input

changes by R(i) ≥ 0 ∈ R

m×m

at time instance k + i.

The time range of the prediction is denoted by H

and

of the input changes by H

. At every time instance

the controller solves the optimization problem

min

gun

(k+i), i=1,...,H

J(k) (46)

subject to 0 ≤ u

gun

(k + i) ≤ 1.

Only the ﬁrst computed input is given to the plant.

The minimization of the cost function is repeated

at every time instance. This is called moving hori-

zon principle. As shown in (Maciejowski, 2002)

the optimization problem (46) can be formulated as

a quadratic programming (QP) problem with con-

straints and thus solved very efﬁciently by standard

QP solvers.

5.2 Closed Loop Simulation

In the following the temperature of the RF plant

should be controlled by the MPC in a closed loop sim-

ulation. The controller gets a reference r

gun

for the

states. We are only interested in the gun temperature

here such that only a reference for this temperature

has to be given

gun

(k+i)=







g,SP

(k+i)







∈R

, i = 1, . . . , H

. (47)

The tuning parameters are on the one hand the predic-

tion and control horizons H

and H

and on the other

the weighting matrices Q and R. Since only the track-

ing of the ﬁrst state, the gun temperature is of interest

only this one has to be weighted with a factor q. The

factor is chosen the same for all times. This results in

a weighting matrix for the states at time i

Q(i) =







q 0 ·· · 0

0 0 ·· · 0







∈ R

6×6

, i = 1, . . . , H

(48)

The weighting of the input changes is done by a

scalar since the system has one input only

R(i) = r, i = 1, . . . , H

. (49)

To achieve a good performance of the overall system,

the controller can be tuned by changing H

, H

, q

and r. The parameters H

and H

are related to the

time that the controller predicts the possible future re-

sponses of the plant. The choice of these parameters is

a tradeoff between prediction and computation time.

The parameters q and r can be tuned to get a tradeoff

between tracking and control effort. A higher q leads

to better tracking but more control effort in general.

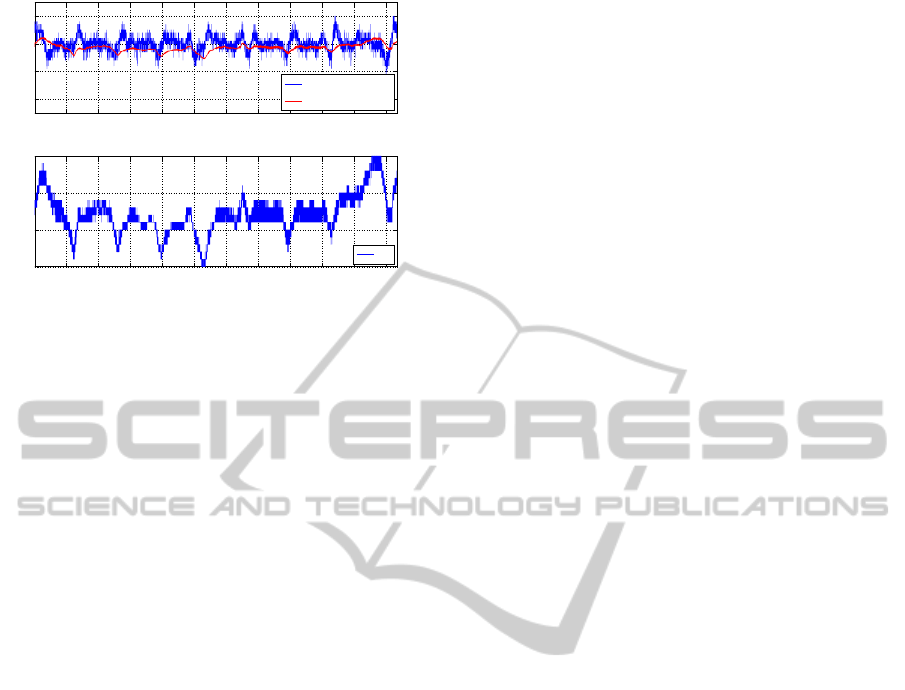
The reference temperature T

g,SP

used here is equal to

61.35

◦

C. This results in a system behaviour shown in

Figure 16. Here the difference between setpoint and

gun temperature is shown for the simulation of the

MPC and measurement data of the device.

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

316

100 200 300 400 500 600 700 800 900 1000 1100

-0.2

-0.1

0.1

Temperature [°C]

g,meas

- T

g,SP,meas

g,MPC

- T

g,SP,MPC

100 200 300 400 500 600 700 800 900 1000 1100

24.5

25.5

Temperature [°C]

Time [min]

Figure 16: Simulation results of the MPC controller.

In the case where the cold water temperature is

constant the controller holds the temperature well ex-

cept a certain small offset due to model differences. A

change in the cold water temperature directly disturbs

the gun temperature. The standard MPC approach ap-

plied here cannot deal with that, because such distur-

bance is not predictable. The controller has to be ex-

tended with some action for disturbance rejection like

integral action.

6 CONCLUSION

A thermal MIMO model of the RF GUN for FLASH

was derived. The model focuses on the cooling circuit

and the inﬂuence of the LLRF to it. Since the struc-

ture of the facility at European XFEL is comparable

to FLASH the structure of the model can be used and

only parameters have to be adjusted.

The RF GUN and the cooling circuit are modeled by

power balances. With that the main dynamics of the

thermal behaviour of the facility are captured. The as-

sumptions that one temperature representing the tem-

perature distribution of the whole RF GUN turned out

to be valid. The parameters of the model were esti-

mated by measurement data. Simulation results show

good ﬁts of the RF GUN temperature dynamics to the

measurement data. In the cooling circuit some differ-

ences between simulated and measured temperature

occur caused by only few measurement information

of the cooling circuit available for parameter identiﬁ-

cation, especially the missing ﬂow information.

With the model a model predictive control approach

is derived in simulation to control the gun temperature

by the cold water valve. A rough approximation of the

LLRF control and a linearization of the model allows

the application of a linear MPC approach. Tuning the

controller by changing the weights of the cost func-

tion and testing it in simulation shows that a predictive

cooling concept can signiﬁcantly improve the stabil-

ity of the RF GUN operation compared to the current

control concept, i.e. less detuning and therefore less

RF power variations leading to constant power dissi-

pation.

In the future the model predictive control concept

can be further developed by adding constraints, dis-

turbance rejection or a nonlinear approach. An im-

provement of the model would be possible with bet-

ter measurement information e.g. by a mobile ﬂow

measurement. Afterwards the controller could be re-

alized on hardware at XFEL and test can be con-

ducted at FLASH. Additionally the model could be

used for other approaches like model-based fault de-

tection. This makes sense because of the high com-

plexity of the whole free-electron laser facility.

REFERENCES

Altarelli, M., Brinkmann, R., Chergui, M., Decking, W.,

Dobson, B., D

usterer, S., Gr

ubel, G., Graeff, W.,

Graafsma, H., Hajdu, J., Marangos, J., Pﬂ

uger, J.,

Redlin, H., Riley, D., Robinson, I., Rossbach, J.,

Schwarz, A., Tiedtke, K., Tschentscher, T., Vartani-

ants, I., Wabnitz, H., Weise, H., Wichmann, R., Witte,

K., Wolf, A., Wulff, M., and Yurkov, M. (2006).

XFEL, the European X-ray free-electron laser: Tech-

nical design report. DESY XFEL Project Group,

Hamburg.

FLASH (2013). Free-electron laser FLASH.

ottmann, K., Paramonov, V., Skasyrskaya, A., and

Stephan, F. (2008). Rf gun cavities cooling regime

study. Desy report, TESLA-FEL 2008-02.

Hoffmann, M., Ayvazyan, V., Branlard, J., Butkowski, L.,

Grecki, M. K., Mavric, U., Omet, M., Pfeiffer, S.,

Schlarb, H., Schmidt, C., Piotrowski, A., Fornal, W.,

and Rybaniec, R. (2015). Operation of normal con-

ducting rf guns with mtca.4. In IPAC - 6th Inter-

national Particle Accelerator Conference, Richmond,

USA. DESY Hamburg, FastLogic Sp. z o.o., Lodz,

Warsaw University of Technology.

Kuchling, H. (1991). Taschenbuch der Physik. Fach-

buchverlag Leipzig, 13. edition.

Ljung, L. (1987). System identiﬁcation: Theory for the

User. Englewood Cleffs, Prentice-Hall.

Ljung, L. (2001). System Identiﬁcation Toolbox. The Math

Works.

Maciejowski, J. (2002). Predictive Control with Con-

straints. Pearson Education Limited.

Mathworks, I. (2014a). Simulink Design Optmization

User’s Guide. The Mathworks Inc.

Mathworks, I. (2014b). Simulink User’s Guide. The Math-

works Inc.

Schilcher, T. (1998). Vector Sum Control of Pulsed Acceler-

ating Fields in Lorentz Force Detuned Superconduct-

ing Cavities. PhD thesis, Hamburg University.

Stephan, F. (2015). private communication. DESY.

HighPrecisionTemperatureControlofNormal-conductingRFGUNforaHighDutyCycleFree-ElectronLaser

317