Performance Evaluation of Meteor Key Distribution

Amir I. Sulimov and Arkadiy V. Karpov

Department of Radio Physics, Institute of Physics, Kazan Federal University, 18

Kremlyovskaya St.,

Kazan, Russian Federation

Keywords: Encryption Key Distribution, Shared Randomness, Meteor Radio Propagation, Meteor Burst Channel,

Carrier Phase, Channel Reciprocity.

Abstract: The Wireless Key Distribution is a fast growing area of applied cryptography covering different approaches

of secure distribution of secret encryption key based on channel stochastic properties in specific radio

communication systems. To be applicable in key distribution purposes the radio channel must meet the three

basic requirements: randomness, reciprocity and spatial selectivity. For a long time it was believed that only

the fading channels in multipath environment could satisfy all the three requirements. However, several

studies also considered a meteor burst channel as a potential candidate for the secure key distribution at

distances up to 2000 km. Unfortunately, a rigorous analysis of meteor radio propagation processes shows

that the channel has only approximate reciprocity. This may result in the two legitimate nodes would not be

able to generate identical copies of the shared secret key indicating that the Meteor Key Distribution is

impossible in practice. In addition, a complicated astronomical nature of the meteor burst channel causes

deep diurnal variation in its performance. The aim of our research was a comprehensive evaluation of

potential performance of the Meteor Key Distribution systems, taking into account all the physical layer

effects of meteor burst channel. We also wanted to clarify, how strong the imperfection of a real meteor

burst channel affects the key distribution feasibility.

1 INTRODUCTION

The problem of secure key distribution plays an

important role in modern cryptography. In recent

decades there has been a shift from mathematical

algorithms of key distribution to the principles of

creating a shared physical source of randomness.

The Quantum Key Distribution (Bennett, 1984)

along with the Wireless Key Distribution (Hershey,

1995) systems should be mentioned as notable

examples of such approach. As for the Wireless Key

Distribution (WKD), it covers different techniques

of secure distribution of a shared secret encryption

key based on channel stochastic properties in

specific radio communication systems. In essence,

the pair of legitimate nodes uses their radio channel

as a source of common randomness to establish a

shared encryption key.

For the radio channel to be applicable in key

distribution purposes, it must meet the three basic

requirements: 1) randomness, 2) reciprocity and 3)

spatial selectivity. The channel randomness provides

high entropy and unpredictability of the shared key.

The channel reciprocity ensures that both legitimate

users to create identical copies of the key. The

spatial selectivity, also referred as a sharp spatial

decorrelation of radio signal parameters, prevents a

key leakage to potential eavesdropper.

In (Sidorov, 2007) a meteor burst channel

(MBC) has been proposed as a candidate for the

secure key distribution over the distances up to 2000

kilometers. We call this method as the “Meteor Key

Distribution" (MKD). The aim of our research was a

comprehensive evaluation of potential performance

of the Meteor Key Distribution systems, taking into

account all the physical layer effects of meteor burst

channel. First of all, we wanted to clarify, whether

the imperfection of a real meteor burst channel

violates the key distribution feasibility and if not,

then how strong it decreases achievable MKD

performance.

In (Sulimov and Karpov, 2014) a randomness of

meteor radio propagation has been justified. In

particular, an unpredictability of the radio

propagation path has been proved. Such path

unpredictability property ensures a carrier phase of

received signal to be a random variable. A pair of

legitimate nodes is able to create two copies of the

392

I. Sulimov A. and V. Karpov A..

Performance Evaluation of Meteor Key Distribution.

DOI: 10.5220/0005568003920397

In Proceedings of the 12th International Conference on Security and Cryptography (SECRYPT-2015), pages 392-397

ISBN: 978-989-758-117-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

shared key simply by measuring values of the carrier

phase at receiving a meteor radio reflection.

However, only one of the three WKD basic

requirements has been justified for the Meteor Key

Distribution to this moment. Moreover, there is a

serious problem in MKD justifying at the second

stage, where the channel reciprocity must be

required. A rigorous analysis of meteor radio

propagation shows that the meteor burst channel

provides only approximate (non-perfect) reciprocity

(Desourdis, 1993). The MBC reciprocity violation

(or simply non-reciprocity) observed in practice

causes some mismatch in copies of the shared secret

key generated by the legitimate parties. This

circumstance substantially decreases a key

generation rate. That is the issue we are going to

address in the following sections.

2 SIMULATION SCENARIO

An implementation of field experiments on channel

non-reciprocity at real meteor radio link is extremely

costly. This makes computer simulation method

quite reasonable to study the MKD processes. As far

as we know, KAMET (Karpov, 2001) is the only

MBC computer model that simulates all basic effects

of the channel non-reciprocity. This model uses an

improved electrodynamic calculations unit based on

rigorous diffraction theory of scattering of radio

waves off the ionized meteor trails (Khuzyashev,

1984). Another advantage of the KAMET model is a

high accuracy of the performance simulation of

meteor burst communication systems. Such accuracy

is achieved through accounting within simulation a

long-term statistics of radar observations on the

influx of meteoroids into the Earth's atmosphere.

Table 1: Technical specifications for the test meteor links.

Specification Link 1 Link 2

Localization of the legitimate

users

Paris-

Colmar

Vienna-

Colmar

Link length 379 km 669 km

Carrier frequency 50 MHz

Transmitted power 2000 Watts

Required signal-to-noise ratio 20 dB

Amplitude threshold level -6 dBμ

Date of key distribution session July 21, 2015

Two test meteor links have been simulated to

perform evaluation of the key generation rate. Table

1 summarizes their technical specifications. We

intentionally used the test links of different lengths

to show that the link geometry and especially the

link length affect crucially the performance of any

type of meteor burst system including MKD. While

the Link1 could be assigned as a short link, the

Link2 has a quite moderate length. Besides, due to

MBC complex astronomical nature its capacity

varies greatly dependent on the session date and

season. Without loss of generality concerning about

MKD feasibility, we chose session date at July 21st.

The following scenario was implied during the

MKD simulation. A pair of legitimate users (say,

Alice and Bob) exchange with a series of sounding

signals through the meteor burst channel in a full

duplex synchronized mode. When an ionized trail

left by burning in the upper atmosphere meteoric

particle arises at the altitudes of 80-110 km, the

sounding signals transmitted simultaneously in

opposite directions by Alice and Bob are reflected

from it to be received at another side of the link. At

receiving the signals Alice and Bob measure their

carrier phase. Due to the MBC stochastic properties

all these measurements are random numbers. By

repeating such exchange with Bob for N times, Alice

collects the {ϕ

}

sample of the carrier phase

measurements. Bob collects the {ϕ

}

sample of

size N in the same manner. Further, Alice and Bob

achieve an agreement on the parameters of the so-

called “bit extraction” procedure (Croft, 2011) to

extract a shared key from their samples. After that,

Alice processes her own sample {ϕ

}

to generate

the Κ

key, and Bob generates the Κ

key by

extracting the random bits from his sample {ϕ

}

the same way as Alice. From each single

measurement of the carrier phase Alice and Bob

were extracting m random bits, where m is the so-

called “codeword length”.

In practice, due to the non-perfect channel

reciprocity and noise factors, the {ϕ

}

and {ϕ

}

samples always have some mismatch Δϕ= |ϕ

– ϕ

As a result, the K

and K

instances of the secret key

also contain some bits in mismatch. To eliminate

them, Alice and Bob had to perform a key

reconciliation procedure. Unfortunately the key

reconciliation leads to some loss in the length of the

final shared key. If we denote its effectiveness as

η, then we can state that η < 100%. According to

(Smolyakov, 2013), the key generation rate R

can

be estimated by the formula (1), where T is the

sample collecting time.

TNmR

/η⋅⋅=

(1)

The two test meteor links (Paris-Colmar and

Vienna-Colmar, respectively) we simulated had

essentially different lengths. As will be shown in the

PerformanceEvaluationofMeteorKeyDistribution

393

following sections, this difference resulted in very

different MKD performance indication.

3 NON-RECIPROCITY OF

METEOR BURST CHANNEL

The channel reciprocity is one of the basic properties

allowing secret key distribution between a given pair

of legitimate nodes. Unfortunately, an absolute

reciprocity is only an idealization of observed

reality. Specifically, the fact that the meteor burst

channel has non-perfect reciprocity inevitably leads

to some key mismatch between Alice and Bob. This

limits achievable key generation rate.

There are three main physical layer mechanisms

that cause the channel non-reciprocity:

1) polarization phenomena at meteor radio

propagation (Khuzyashev, 1984);

2) multipath fading effects due to scattering

from meteor trails with several reflecting

points (Weitzen, 1987);

3) random drift of the trail reflecting point due

to ionospheric turbulent winds (Weitzen,

1987).

All these mechanisms are included into the KAMET

simulation model allowing them to be accounted

within our MKD performance evaluation.

The polarization phenomena are the dominant

factor of the MBC non-reciprocity. This follows

from the fact that the characteristics of scattered

signal depend mainly on the polarization of the

incident radio wave. Looking deeper, we find that

two radio waves transmitted by Alice and Bob in the

opposite directions experience different polarization

rotations during their propagation. This is due to

non-symmetric geometry of the uplink propagation

accompanied with the influence of the Faraday

Effect in a magnetized ionosphere. As a result, the

incident waves transmitted by Alice and Bob have

different polarizations. This causes non-symmetric

scattering of opposite signals off the meteor trail and

in the end it results in the channel non-reciprocity.

We also took into account effects of the meteor

trail decay with continuous changing in time of its

scattering properties. Therefore, level of channel

non-reciprocity constantly varies during the signal

detection time. For the key distribution purposes,

Alice and Bob should choose the time point that

corresponds to the lowest value of phase non-

reciprocity (Sulimov, 2014). By accounting all the

above mentioned non-reciprocity effects, we were

able to properly simulate limitations on the key

distribution process caused by physical layer of

channel. Let us consider the simulation results next.

Figure 1 shows a probability distribution

histogram of the phase mismatch Δϕ = |ϕ

– ϕ

simulated for the test Link 1 (Paris-Colmar). As can

be seen, the phase mismatch Δϕ typically shows a

symmetric shape of probability distribution with a

zero mean value. The histogram standard deviation

was σ(Δϕ) = 16.1°, and we should admit here that

this is a relatively high value with non-negligible

impact. The test Link 2 (Vienna-Colmar) showed a

similar histogram but with slightly lower standard

deviation: σ(Δϕ) = 14.2°. It should be noted that

even such a small decrease in the standard deviation

σ(Δϕ) allowed 24% higher key reconciliation

efficiency η than achieved at the Paris-Colmar link.

Figure 1: Probability distribution histogram of mismatch

in the phase measurements of legitimate users observed at

the Paris-Colmar meteor link (session time is 3 a.m.).

The simulation results also revealed that a certain

amount η

of detected meteor trails had an

extremely high non-reciprocity. Obviously, such

"extremely" non-reciprocal trails could not be used

for the key distribution purposes. About η

= 3.2%

of all the trails detected at the Paris-Colmar link

were recognized as extremely non-reciprocal. The

same indicator for the Vienna-Colmar link showed

the value about η

= 1.2%.

As will be shown in the Section 5, the presence

of phase mismatch significantly limits achievable

key generation rate. However, a meteor activity

during the key distribution session is another

essential factor that defines the key generation rate.

The next section presents our simulation results of

the meteor activity for both test meteor links.

4 DIURNAL VARIATIONS OF

METEOR ACTIVITY

The meteor activity and performance of meteor burst

SECRYPT2015-InternationalConferenceonSecurityandCryptography

394

channel experience a strong diurnal variation

(McKinley, 1961). According to formula (1), the key

generation rate should follow these variations too.

The diurnal dependence is a legacy of the MBC

astronomical nature. In practice, current meteor

activity is usually characterized by the number of

meteor trails N

detected per 1 hour (the hourly

number of meteors). In this case, the (N/T) multiplier

in the formula (1) should be substituted by

)3600/()1(

HNR

N⋅η− . The KAMET simulation

model we used is based upon a long-term (about

several decades) statistics of radar observations on

the meteoric matter influx. This allows accurate

prediction of diurnal variations in the meteor activity

for a given radio link. Let us consider the simulation

results obtained for the test meteor links.

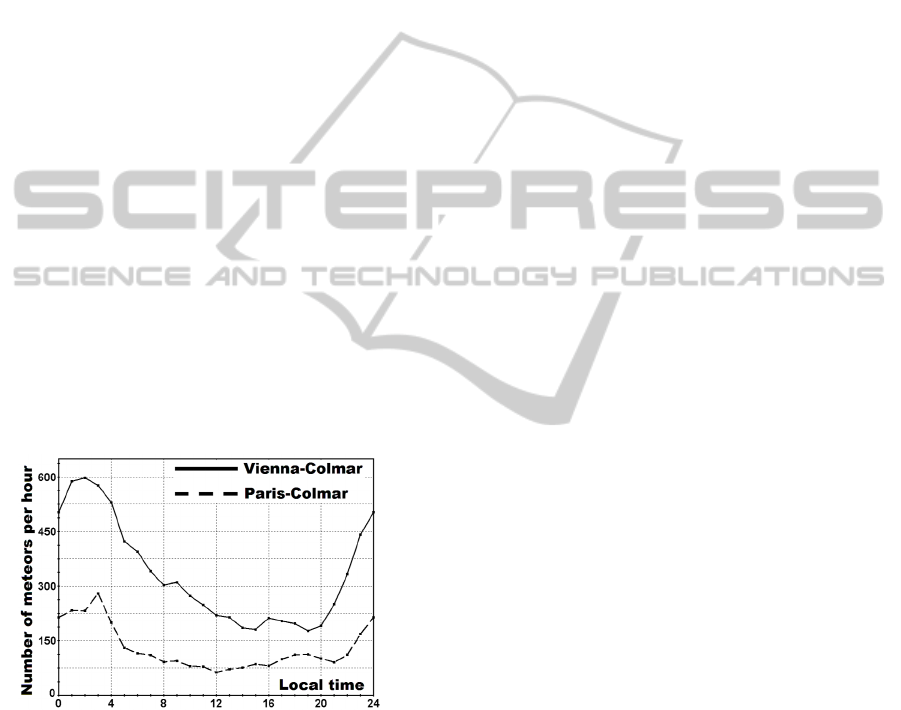
Fig. 2 presents the diurnal variations in the

meteor activity simulated for both test links. As all

the legitimate nodes had close geographic latitudes,

the curves reveal very similar profiles but differ

greatly in the number of detected meteor trails. The

maximum meteor activity with hourly number

= 280 at the Paris-Colmar link was observed at 3

a.m. local time. The minimum meteor activity with

= 63 was observed at 12 a.m. Similarly, at the

Vienna-Colmar link the maximum meteor activity

with N

= 598 was observed at generating the shared

key at 2 a.m. local time. The minimum activity with

hourly number N

= 181 was observed at 3 p.m.

Figure 2: Diurnal variations in meteor activity simulated

for the test meteor links.

As we can see, the depth of diurnal variations in

meteor activity may reach up to 400%. Another

feature of meteor burst communications is a low

performance at shorter radio links. Moreover, an

accurate analysis shows that the MBC non-

reciprocity reveals some daily changes too.

However, these changes affect the MKD

performance much weaker than the variations in

meteor activity. To be precise, it’s about 15% versus

400% in depth. Thus, we should seek a maximum

possible hourly number N

in the first place in

practice.

From the practical point of view, the greatest

interest is to estimate a gap between the maximum

and minimum MKD performance indications.

Considering this, for each test link we present the

performance evaluation corresponding only to the

maximum and minimum values of meteor activity.

5 EVALUATION OF KEY

GENERATION RATE

After collecting the {ϕ

}

and {ϕ

}

samples of

carrier phase measurements for all detected meteor

radio reflections Alice and Bob were able to

generate the K

and K

copies of the secret key,

respectively. To generate them, Alice and Bob

implemented a so-called “bit extraction” procedure

following the algorithm presented in (Sulimov and

Smolyakov, 2014). Since (Sulimov and Karpov,

2014) proved an absence of autocorrelation within

the sample of carrier phase measurements, no

sample decorrelation procedure was required to

create the key.

As long as meteor burst channel always causes

some mismatch in phase measurements of Alice and

Bob, a key reconciliation procedure is required. We

used the cyclic redundancy codes (CRC-16) for the

and K

reconciliation. This is similar to a more

secure approach based on the privacy amplification

(Bennet, 1995) but easier to implement. In this case,

the choice of optimal codeword length m* for the bit

extraction procedure becomes a crucial moment.

Increasing the value of m we can extract more

random bits from each single carrier phase

measurement but causing a higher key mismatch rate

. It’s a trap, because high key mismatch rate may

result in total rejection of the key at its

reconciliation.

Fig. 3 presents the key mismatch rate (i.e. the

probability of mismatch in a single bit) as a function

of the codeword length m used in the bit extraction

procedure. We can see an asymptotic rise of the key

mismatch rate up to the p

= 50% value as the

codeword length m is increased. Due to the channel

non-reciprocity and noise factors, even at the

smallest possible value of m = 1 bit per measure a

very high key mismatch rate is observed: p

= 4.7%

(for the Paris-Colmar link) and p

= 3.5% (for the

Vienna-Colmar link), respectively. At first glance,

the obtained values of the key mismatch rate are

unacceptably high, but such mismatch levels are

PerformanceEvaluationofMeteorKeyDistribution

395

quite typical for the WKD practice. We can refer to

the (Liu, 2014) research as an example of the recent

experimental results.

Figure 3: Key mismatch rate as a function of the codeword

length.

During the key reconciliation each block of l

key sequence bits in length had been verified with

the CRC-16 code. After successful block verification

we excluded 16 arbitrary bits from this block to

prevent a key leakage caused by the CRC-code

transmission. For each value of the codeword length

m we were looking for an optimal verification block

length l

* that provided a maximum efficiency of the

key reconciliation η∗. This was done, because a

short verification length l

leads to a strong loss in

the verified key size after excluding 16 arbitrary bits

from the reconciled block. At the same time, the

longer the block size l

the higher probability of the

mismatch and reconciliation failure.

Table 2: Optimization of the codeword length (Link2 at 2

a.m.).

m, bit corr(K

) p

,% l

*, bit η(l

*), % R

, bph

1 0,931 3,45 33 15,46 91,4

2 0,893 5,34 32 13,05 154,3

3 0,840 8,02 30 8,88 157,4

4 0,763 11,87 24 4,50 106,3

5 0,671 16,43 23 1,82 53,7

6 0,579 21,06 22 0,763 27,1

7 0,501 24,95 21 0,295 12,2

8 0,439 28,03 20 0,114 5,4

9 0,394 30,31 20 0,047 2,5

10 0,356 32,19 20 0,036 2,1

11 0,344 32,64 20 n/a n/a

Table 2 shows an example of the codeword

length optimization for the Vienna-Colmar test link

(session time 2 a.m.). The second column presents

the cross-correlation coefficient corr(K

) of the

and K

key instances, which is a linear function

of the key mismatch rate p

. The maximum key

generation rate (in bits per hour) was achieved at

m* = 3 bits per measure. The table string with

corresponding performance indicators is highlighted

in bold.

Resulting estimates of the key generation rate R

based on the formula (1) are presented in Fig. 4 (test

Link 1) and Fig. 5 (test Link 2), respectively. For

each test link we present the codeword optimization

curves at the minimum and maximum levels of

meteor activity. Due to a high mismatch in the phase

measurements of Alice and Bob the optimal

codeword length m* had very low values: m* = 2 or

m* = 3. Low values of meteor activity resulted in a

very humble MKD performance with maximum key

generation rate R

less than 160 bits per hour.

Figure 4: Key generation rate as a function of the

codeword length (Paris-Colmar meteor link).

Figure 5: Key generation rate as a function of the

codeword length (Vienna-Colmar meteor link).

Taking into account all the diurnal variations in

the MKD performance observed at the Paris-Colmar

link, Alice and Bob were able to generate a shared

key with total length of 571 bits for a 24 hour

period. Thanks to a higher meteor activity, similar

estimates performed for the Vienna-Colmar link

show the key length about 2081 bits per 24 hours

day.

SECRYPT2015-InternationalConferenceonSecurityandCryptography

396

Summarizing our results, we can conclude that,

despite non-perfect reciprocity of meteor burst

channel, the Meteor Key Distribution is feasible in

practice. Physical parameters of each individual

meteor link essentially affect the performance of the

key distribution process making it unique for the

given radio link. Despite the humble key generation

rate, we believe that MKD systems could be useful

in practice. Their advantages are much greater key

distribution distances (up to 2000 km), low cost

equipment, vitality and ability to operate under

conditions of severe climate such as in polar and

other remote regions.

6 CONCLUSIONS

Our study presents the very first attempt to evaluate

a performance of Meteor Key Distribution systems

with an account of full complex of the physical layer

effects of meteor burst channel (MBC). To deal with

the channel non-reciprocity and diurnal variations

effects, we used a MBC simulation model with

improved electrodynamic and astronomical

calculations unit.

Our simulation results proved that, despite non-

perfect reciprocity of meteor burst channel, the

Meteor Key Distribution is feasible in practice.

Physical parameters of each individual meteor link

essentially affect the performance of the key

distribution process making it unique for the given

radio link. The main factor limiting key generation

rate is low meteor activity and its diurnal variation.

As show presented estimates, a shared key of 571

bits in length could be generated for a 24 hour

period at the Paris-Colmar meteor link with a peak

key generation rate about 59 bits per hour. Similar

estimates performed for the Vienna-Colmar meteor

link show 2081 bits as a daily key length with a peak

rate about 157 bits per hour, respectively.

Despite the humble key generation rates

presented, we believe that MKD systems could be

useful in practice. Specifically, they might be used

for key distribution at up to 2000 km distances in

such applications as AES, lightweight cryptography

like CLEFIA, and hash-based post-quantum

subkeys.

As we stated in the beginning, for the radio

channel to be applicable in key distribution

purposes, it must meet the three basic requirements:

1) randomness, 2) reciprocity and 3) spatial

selectivity. Hence, the spatial selectivity of meteor

burst channel must be addressed at the next stage of

justification of the Meteor Key Distribution systems.

REFERENCES

Bennett, C. H., Brassard, G., 1984. Quantum

Cryptography: Public key distribution and coin

tossing. In Proc. of IEEE Int. Conf. on Computers,

Systems and Signal Processing, pp. 175-179.

Bennett, C. H., Brassard, G., Crepeau, C., Maurer, U. M.,

1995. Generalized privacy amplification. In IEEE

Trans. on Inf. Theory, vol.41, iss.6, pp. 1915-1923.

Croft, J. E. D., 2011. Shared secret key establishment

using wireless channel measurements. Ph.D. thesis,

Dept. Elect. Eng., University of Utah, USA.

Desourdis, R. J., Wojtaszek, H., Sidorov, V. V. et al.,

1993. Nonreciprocity of Meteor Scatter Radio Links.

In IES’93, Proc. of Ionosph. Effects Symp., pp. 165-

173.

Hershey, J. E., Hassan, A. A., Yarlagadda, R., 1995.

Unconventional cryptographic keying variable

management. In IEEE Trans. on Communications, vol.

43., iss.1, pp.3-6.

Karpov, A., Tereshin, S., Abrosimov, J., 2001. The

computer model “KAMET”: The new generation

version. In Proc. of the Meteroids 2001 Conf., pp.367-

370.

Khuzyashev, R. G., 1984. Calculation of the amplitude

and phase characteristics of a signal scattered

obliquely off a meteor trail. In Radiophysics and

Quantum Electronics, vol.27, iss.9, pp.778-782.

Liu, H., Yang, J. et al., 2014. Group Secret Key

Generation via Received Signal Strength: Protocols,

Achievable Rates and Implementation. In IEEE Trans.

on Mobile Computing, vol.13, iss.12, pp.2820-2835.

McKinley, D. W. R., 1961. Meteor science and

engineering, McGraw-Hill, 309 p.

Sidorov, V. V., Karpov, A. V., Korneev, V. A., Nasyrov,

A.F., 2007. Meteor Time Transfer and Meteor

Cryptography. In TimeNav’07, Proc. of 21st European

Frequency and Time Forum, pp. 315-317.

Smolyakov, A. D., Sulimov, A. I., Karpov, A. V.,

Sherstyukov, O.N., 2013. Experimental Verification of

Possibility of Secret Encryption Keys Distribution

with a Phase Method In a Multipath Environment. In

SIBCON-2013, Proc. of 2013 IEEE Int. Siberian Conf.

on Control and Communications.

Sulimov, A.I., Karpov, A.V., 2014. Secure Key

Distribution based on Meteor Burst Communications.

In Proc. of the 11th Int. Conf. on Security and

Cryptography (SECRYPT-2014), pp. 445-450.

Sulimov, A. I., Smolyakov, A. D., Karpov, A. V.,

Sherstyukov, O.N., 2014. Experimental Study of

Performance and Security Constraints on Wireless

Key Distribution Using Random Phase of Multipath

Radio Signal. In Proc. of the 11th Int. Conf. on

Security and Cryptography (SECRYPT-2014), pp.

411-416.

Weitzen, J. A., Sowa, M., Scofidio, R., Quinn, J., 1987.

Characterizing the Multipath and Doppler Spreads of

the High-Latitude Meteor Burst Communication

Channel. In IEEE Trans. on Communications, vol.35,

pp.1050-1058.

PerformanceEvaluationofMeteorKeyDistribution

397