
Mathematical Modeling for Ship Evacuation from Tsunami Attack
Ei-ichi Kobayashi
1
, Shota Yoneda
1
, Masako Murayama
2
, Yuuki Taniguchi
1
,
Hirotada Hashimoto
1
and Shunichi Koshimura
3
1
Graduate School of Maritime Sciences, Kobe University, 5-1-1 Fukae-minami, Higashinada-ku, Kobe, Japan
2
Toyama National College of Technology, 1-2 Ebie-neriya, Imizu city, Toyama, Japan
3
International Research Institute for Disaster Science, Tohoku University, Sendai, Tohoku, Japan
Keywords: Tsunami Disaster, Ship Evacuation, Maneuverability.
Abstract: When a tsunami warning is officially announced, as a measure for safeguarding ships from tsunami attacks,
it is recommended that large ships in harbors be maneuvered to sheltered areas outside the ports until the
tsunami subsides. In this paper, we develop mathematical simulation models to describe the dynamic
behavior of a ship. Then, the evacuation maneuvers of a cruise ship and a cargo ship in a tsunami flow are
analyzed and characterized. Finally, it is concluded that this kind of simulation could be very great help
useful to evaluate the safety of ship evacuation methods against for the tsunami attacks.
1 INTRODUCTION
For over 1,000 years, large earthquakes have
occurred along the Nankai Trough located in the
Pacific Ocean off Shikoku Island and Ki-i Peninsula
of Honshu Island, Japan, where the Eurasian Plate is
subducting under the Philippine Plate. There is an
increasing concern that a large earthquake may
occur along the Nankai Trough in the Pacific Ocean
near Japan, where the Tōkai, Tōnankai, and Nankai
regions are located (the earthquakes in these regions
are discussed hereinafter). Tsunamis have caused
great damage along the coastal areas near the Tōkai,
Tōnankai, and Nankai regions. Earthquakes of a
magnitude as high as 8.0 on the Richter scale have
occurred at these three locations in the past 1,500
years. For example, the earthquake that struck
Hakuhou in AD 684 was of a magnitude of 8.0 on
the Richter scale. Other incidents include the
earthquakes at Keicho in AD 1605 (magnitude: 7.9),
at Houei in AD 1707 (magnitude: 8.6), at Tōnankai
in AD 1944 (magnitude: 8.4), and at Nankai in AD
1946 (magnitude: 8.4). As of January 1, 2015, the
probability of the occurrence of earthquakes at
Nankai and Tōnankai in the next 30 years is
estimated as 70% (Figures 1 and 2).
It is estimated that the time taken by a tsunami to
arrive at the Osaka Bay after an earthquake is
approximately 1 h. A tsunami wave on the coast of
Japan would not only increase the sea level but also
create strong horizontal flows in bays and ports.
Consequently, ships may move uncontrollably,
subjecting piers to tremendous sideways forces, and
crash relentlessly against breakwaters. Ultimately,
vessels would set adrift and run aground.
To safeguard ships from tsunami attacks in
Osaka bay and nearby areas, when a tsunami
warning is officially announced, it is recommended
that large general merchant vessels in harbors be
maneuvered to sheltered areas outside the ports until
the tsunami subsides.
However, the guidelines provided by port
authorities only state that ships must leave ports
immediately if a tsunami attack is expected and do
not clearly indicate how the ships can navigate and
where they can relocate.
Computer simulation is one of the most valuable
and reliable techniques for developing appropriate
evacuation plans for ships in ports if a tsunami is
expected. There are numerous ports used by
container ships, cargo ships, passenger ships, ferries,
pleasure ships, and/or fishery boats along the coastal
area of Osaka Bay, Japan. Cruise ships that regularly
enter and depart from Osaka Bay are capable of
carrying over 3,500 passengers. Moreover, large
cargo ships are often docked at the Osaka Bay.
In this paper, mathematical simulation models to
describe the dynamic behavior of a ship are
318
Kobayashi E., Yoneda S., Murayama M., Taniguchi Y., Hashimoto H. and Koshimura S..
Mathematical Modeling for Ship Evacuation from Tsunami Attack.
DOI: 10.5220/0005569103180325
In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),
pages 318-325
ISBN: 978-989-758-120-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

developed. Then, the evacuation maneuvers of
tankers and a cruise ship in a tsunami flow are
analyzed and evaluated.
Figure 1: Locations of Tōkai, Tōnankai, and Nankai
Trough.
Figure 2: History of earthquakes in the Tōkai, Tōnankai,
and Nankai trough.
2 MATHEMATICAL MODELS OF
TSUNAMI AND SHIP MOTIONS
2.1 Tsunami Simulation
Tsunamis are normally generated by ocean-trench
earthquakes in which ocean plates sink under
continental plates. When the plate boundaries reach
their strain limits, the edge of the continental plate
springs back, resulting in an ocean-trench
earthquake. A mathematical model for a tsunami
was used to predict the tsunami arrival velocities and
sea-surface elevation in the Osaka and Wakayama
areas. Figure 3 shows the tsunami characteristics in a
coordinate system, formulated by Imamura (1996) as
expressed by Equation (1).
=+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
0
0
0
0
2
00
00
2
0
00
ρ
τ
η
ρ
τ
η
η
y
x
y
gD
D
N
yD
MN
xt
N
x
gD
D
MN
yD
M
xt
M
y
N
x
M
t
(1)
Here, η is the elevation from still sea water; h is the
depth of the still sea water; t is time; x
0
and y
0
represent the coordinate system; g is the
gravitational acceleration; ρ is the water density; D
is the water depth (=h+η); τ
x
and τ
y
are the sea-
bottom friction components in the x
0
and y
0
directions, respectively; and M and N are the flow-
volume fluxes in the x
0
and y
0
directions,
respectively.
Figure 3: Coordinate system for tsunami simulation.
Figure 4 shows the time history of the elevation
of the sea surface. Figures 5 and 6 show the time
histories of the velocity components resulting from
earthquakes at the east and north sides of the
Shimotsu port, respectively.
The sea-surface elevation exceeds 1.5 m during
the first tsunami attack and 2 m during the second
attack, 2,500 and 6,500 s after the earthquake,
respectively. The rise and fall of the surface
elevation repeat at intervals of approximately 1,000
to 2,000 s. The horizontal flow caused by the
tsunami increases slowly after the earthquake. The
northward flow, which is the dominant component
of the horizontal flow induced by the tsunami,
reaches a maximum value of 1.5 m/s at the time of
the sea-surface elevation peak.
h
η
y
0
x0
z
o
MathematicalModelingforShipEvacuationfromTsunamiAttack
319

Figure 4: Computed sea-water level during tsunami in
Shimotsu.
Figure 5: Velocity components resulting from earthquake
at east side of Shimotsu port during tsunami in Shimotsu.
Figure 6: Velocity components resulting from earthquake
at north side of Shimotsu port during tsunami in Shimotsu.
Figure 7 shows the time histories of the sea-
surface elevation and velocity components for the
Akashi channel.
The elevation exceeds 1.7 m during the first
tsunami attack and 2 m during the second attack,
4,000 and 8,000 s after the earthquake, respectively.
These data are used for simulations in Scenario
2, which is described later.
Figure 7: Time histories of velocity and elevation of
tsunami at Akashi Strait.
2.2 Ship Maneuverability
Horizontal ship motions such as surge, sway, and
yaw are expressed by Equation (2) to Equation (12),
formulated by Kobayashi (1995, 2006), using the
coordinate system shown in Figure 8.
Figure 8: Coordinate system for maneuvering motion.
The basic inertia for a ship is expressed as follows:
(
+
)
−+
+
−
(
−
)
−
+
=
+
+
+
+
(
+
)
−
(
+
)
−
+
=
+
+
(
+
)
=
+
+
(2)
where
x
mm,
, and
y
m
are the mass of the ship and
the added masses of the ship in the
x and y
directions, respectively;
zz
I
and
zz
J
are the mass
moment of inertia and the added mass moment of
inertia of the ship about the z-axis, respectively;
v
u,
are the velocity components in the
00
, yx
directions, respectively;
00
,
cc
vu are the horizontal
velocity components caused by the tsunami in the
00
, yx
directions, respectively;
r
is the rate of turn
of the ship;
HH
YX ,
, and
H
N
are the longitudinal
and lateral forces and the yaw moment acting on the
ship’s hull, respectively;
PP
YX ,
, and
P
N
are the
longitudinal and lateral forces and the yaw moment
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
320

acting on the propellers, respectively;
,,
RR
YX
and
R
N
are the longitudinal and lateral forces and the
yaw moment acting on the rudder, respectively.
This mathematical model is based on one of the
most suitable and commonly used expressions in the
field of ship maneuverability: the MMG
(Maneuvering Modeling Group in Japan) standard
method, which was explained by Yasukawa (2014)
and expanded for maneuvering motions in tsunami
conditions.
2.3 Hull Force
The hydrodynamic forces and yaw moment acting
on a ship’s hull—
HH
YX ,
, and
H
N
—are expressed
as follows:
()
cDXcH
CLdUX
θ
ρ
2
2
=
()
dHCLdUY
cDYcH
/,
2
2
θ
ρ
=
()
dHCdULN
cDNcH
/,
2
22
θ
ρ
=
()
dHrN
r
/,+
,
(3)
where ,, and are ship length, draft, and water
depth;
and
are elative flow velocity and
direction; is density of sea water;
,
, and
are longitudinal and lateral drag of currents
coefficient and currents moment coefficient that are
functions of
and H/d, respectively;
is yawing
moment during turning motion as follows.
(
)
=
2
−
64
|
|
(4)
The yawing moment acting on a hull is affected by
the water depth as follows:
(ℎ)
()
=
1
1
2
+
2
(5)
where
= 0.5 is adopted (Kobayashi 1995), and k
is an empirical value. Considering the shallow-water
effect,
is expressed as follows:
=
1+
(6)
where
,
, and are a drag coefficient for deep-
water conditions, a drag coefficient for shallow-
water conditions, and an empirical coefficient
representing the shallow-water effect. Moreover,
and
are expressed as functions of the draft of a
ship to the water-depth ratio as follows:
(
ℎ
)
(
)
=
−
8
2
(7)
(
ℎ
)
(
)
=
−
8
2
(8)
where
,
are obtained empirically.
2.4 Propeller Force
The equations for the propeller forces and moment
are
=
(
1−
)
=0
=0
(9)
=ρ
,
(10)
where is thrust deduction factor; is thrust of
propeller;
is propeller revolution;
is propeller
diameter;
is thrust coefficient, respectively.
2.5 Rudder Force
The rudder forces and moment are assumed to be
zero when the propeller thrust is zero or negative.
The following expressions are adopted when the
propeller ahead is operating:
=−
(
1+
)
=−1+
=−
(
1+
)
∙
,
(11)
where
is rudder normal force; is rudder angle;
,
and
are interaction coefficients;
is
coordinate of rudder, respectively.
The rudder force is calculated from the velocity
components of the lateral flow at the rudder position
as follows:
MathematicalModelingforShipEvacuationfromTsunamiAttack
321
=
1
2
sin
=
+
=−
(
1+
)
cos∙
=∙
1+
8
=∙
(
+
∙′)
=−tan
(
−
/
)
,
(12)
where
is rudder area;
is gradient coefficient of
rudder normal force =
.
.
;
is effective
rudder angle;
is velocity toward rudder;
is
component of velocity;
is ycomponent of
velocity; and are propeller acceleration
coefficients;
is empirical coefficient; (
+
)
is experimental characteristics on inflow direction to
rudder, respectively.
We solved the differential equations above and
calculated time histories for values such as the ship
velocity, position, and yawing. Then, we simulated
an evacuation maneuver of the ship, assuming the
condition of the currents. This condition was added
as a horizontal flow, which was determined
according to the tidal currents and tsunami
calculation. In these simulations, we ensured the
auto-preservation of the route using a simple
autopilot function. The following automatic rudder-
control algorithm was adopted for the ship to
navigate along the designated route:
∗
=−
Δ−
Δ−
,
(13)
where
∗
, Δy, Δψ, and r are the command rudder
angle, lateral deviation from the route, deviation
from the designated course, and yaw rate,
respectively; and
,
, and
are the empirical
feedback gains.
As the result, the ship in this simulation was
directed along the designated evacuation course.
3 SHIP-EVACUATION
SIMULATION
3.1 Scenarios of Ship Evacuation from
Tsunami Attack
We apply the proposed mathematical model to
evaluate the possibility of safe ship evacuation in
three cases.
3.2 Scenario 1
Few studies for safe ship evacuation have been
conducted in the Wakayama area under tsunami-
induced flow conditions, although studies have been
performed for the Osaka Bay, where numerous
coastal industrial facilities are located. However, it
takes less time for a tsunami to reach the Wakayama
area than the Osaka area. Power plants are located
along the western coast of the Wakayama area, and a
large number of ships carrying dangerous materials
such as crude oil constantly travel there. Thus, the
ability of ships to evacuate to sheltered areas is
verified by performing a dynamic computer
simulation of ship traffic.
We select a very large crude oil carrier (VLCC)
as a target ship for the validation and application of
the model. The principal dimensions of the ship are
presented in Table 1.
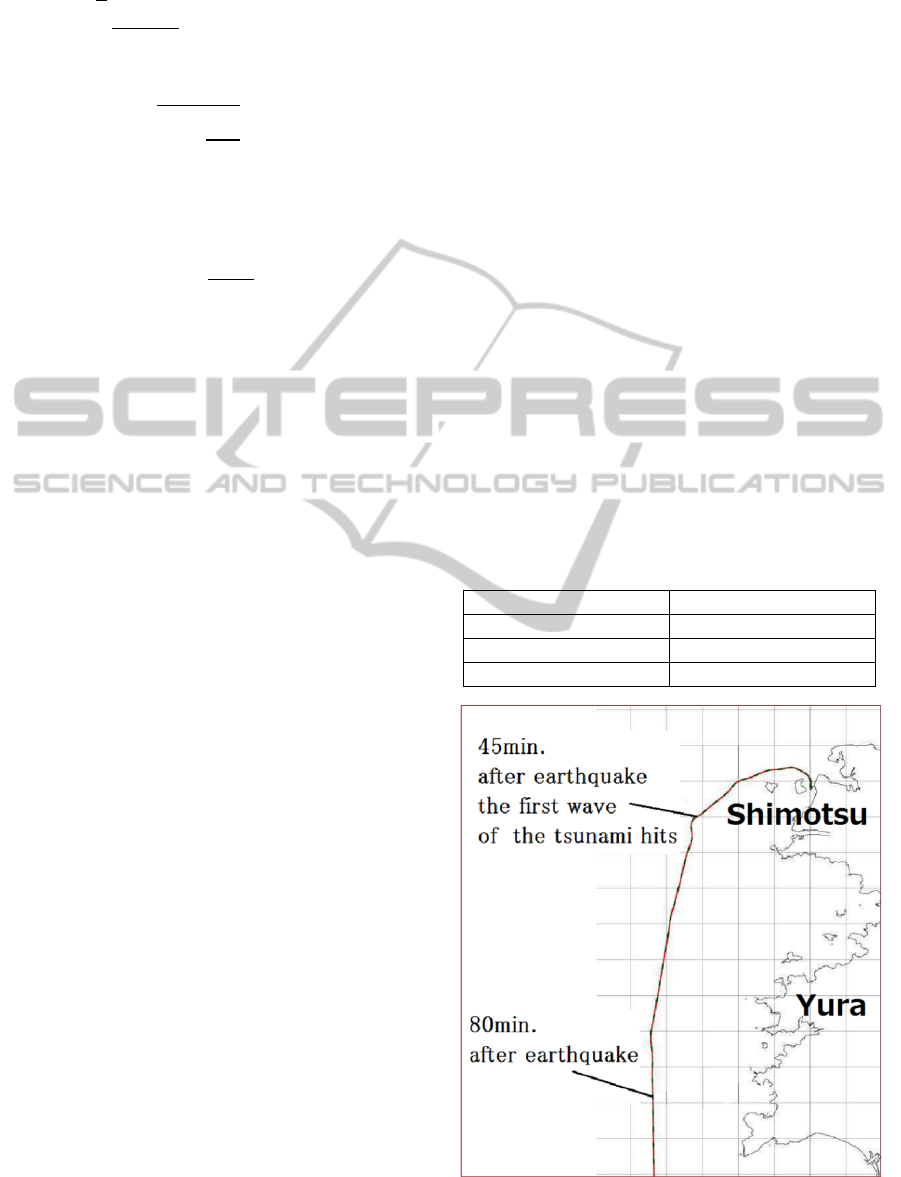
In the evacuation computer simulations, the
initial location of the ship was a berth at the
Shimotsu port. The ship was oriented parallel to the
berth, assuming conditions of outbound berthing. It
was assumed that the tsunami warning was received
Table 1: Principal dimensions of target ship.
Overall length 333 m
Breadth 60 m
Draft 20.943 m
Dead weight 311,141 t
Figure 9: Locus of a ship evacuating the bay after a
tsunami warning.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
322

Figure 10: Time histories of ship speed, rudder angle, and
yaw angle of the VLCC in tsunami evacuation maneuver.
5 min after the earthquake and that the preparation
for departure takes 20 min. Figure 10 shows the
ship’s locus in an evacuation maneuver to avoid a
tsunami that was used in the computer simulation.
Red line, green line and blue line show the rudder
angle, ship’s velocity and yaw angle respectively in
Figure 11. It was verified from these simulations that
the evacuation maneuver can be performed smoothly
and safely because the steering conditions are
normal and the locus of the ship during the
evacuation is moderate.
3.3 Scenario 2
Recently, the local government has been trying to
invite large passenger ships to Osaka, Japan to
expand its local economy. These ships generally
have more than 3,000 passengers and crew onboard,
and people can be severely harmed by accidents
such as collisions or capsizing due to a tsunami.
Accordingly, evaluating and validating safe
evacuation plans for ships in the event of a tsunami
is very important. We propose a safe evacuation
maneuver for a large passenger ship from a berth in
Osaka Port shown in Figure 12 using the
aforementioned mathematical model and computer
simulations.
The principal dimensions of the passenger ship is
listed in Table 2. The locus of passenger ship
evacuating from tsunami attack by the simulation is
shown in Figure 13. It is shown that straight running
to tsunami after turning from the inbound berthing
condition is successfully done.
Table 2: Principal dimensions of passenger ship.
Overall length 310 m
Breadth 39 m
Draft 8.80 m
Gross tonnage 130,000 t
Figure 11: Location of representative ports in Osaka Bay.
Figure 12: Locus of passenger ship evacuating from
tsunami attack.
3.4 Scenario 3
There are several scenarios for ships in Osaka bay,
such as staying and mooring at the berth; anchoring
just outside the port; evacuation to a safe, distant
area; and low-speed maneuvering to head for
tsunami direction by a ship officer’s manual control.
The computer simulation indicates that the hopeful
method most likely to succeed is evacuation to the
west part of the outside of the bay, by passing
through the Akashi channel, which is 3,500 m in
width. A tanker ship is selected according to an
analysis of the traffic through the channel. The
principal dimensions of the ship are presented in
Table 3.
MathematicalModelingforShipEvacuationfromTsunamiAttack
323

The locus of the tanker evacuating from the
Sakaisenboku Port to a west area located to Akashi
channel is shown in Figure 14. The time histories of
yaw angle and rudder angle are shown in Figure 15
and Figure 16 respectively. It seems that the ship can
evacuate the west area safely because the variations
of those values are not so large.
Figure 13: Locus of ship evacuating from tsunami attack.
Figure 14: Time history of yaw angle of target ship
navigation at Akashi Strait.
Figure 15: Time history of rudder angle of target ship
navigation at Akashi Strait.
Table 3: Principal dimensions of middle-class tanker.
Overall length 310 m
Breadth 39 m
Draft 8.80 m
Gross tonnage 160,000 t
4 CONCLUSIONS
In this paper, we showed mathematical simulation
models to describe the dynamic behavior of a ship.
Then, the evacuation maneuvers of a cruise ship and
a cargo ship in a tsunami flow are analyzed and
characterized by simulations based on the models.
Finally, it is shown that a tanker can evacuate to a
safe area outside the port from a berth at the
Shimotsu port, which is relatively close to the
hypocenter of the Nankai and Tonankai earthquakes.
It is also shown that a large passenger ship can
evacuate safely to an area outside the port before the
first strong tsunami attack. Moreover, it is shown
that another type of tanker can evacuate the western
area through the Akashi channel before the attack.
This kind of simulation could be very useful to
evaluate the safety of ship-evacuation methods for
tsunami attacks.
And furthermore, we consider it is important to
verify the accuracy of the models and apply the
method to other scenarios to obtain more effects on
ships due to tsunami.
ACKNOWLEDGEMENTS
The authors express sincere appreciation to Mr.
Shichi and Mr. Yurugi for their assistance with the
present study. This work was supported by JSPS
KAKENHI Grant Nos. 25249128, 24710193 and
15K14263.
REFERENCES
Imamura, F., 1996. Review of Tsunami Simulation with a
Finite Difference Method. Long-Wave Run-up Models.
World Scientific, River Edge, New Jersey.
Kobayashi, E., 1995. The Development of Practical
Simulation System to Evaluate Ship Maneuverability
in Shallow Water. Proceedings of the Sixth
International Symposium on Practical Design of Ships
and Mobile Unites (PRADS ’95). pp. 1.712-1.723.
Kobayashi, E., 2005. A Basic Study on Ship Drifting by
Tsunami. Journal of the Kansai Society of Naval
Architects, Japan. Vol. 243, pp. 49-56.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
324

Kobayashi, E., 2006 A Basic Study on Evacuation
Maneuver from Tsunami Attack, Journal of Japan
Institution of Navigation. Vol. 114, pp. 157-163.
Yasukawa, H., 2014. Introduction of MMG standard
method for ship maneuvering predictions, Journal of
Marine Science and Technology. March 2015, Vol. 20,
Issue 1, pp. 37-52.
MathematicalModelingforShipEvacuationfromTsunamiAttack
325
