
Fast and Robust Keypoint Detection in Unstructured 3-D Point Clouds
Jens Garstka and Gabriele Peters
Human-Computer Interaction, Faculty of Mathematics and Computer Science,
University of Hagen, D-58084 Hagen, Germany
Keywords:
3-D Keypoint Detection, 3-D Recognition, 3-D Computer Vision.
Abstract:
In robot perception, as well as in other areas of 3-D computer vision, keypoint detection is the first major
step for an efficient and accurate 3-D perception of the environment. Thus, a fast and robust algorithm for an
automatic identification of keypoints in unstructured 3-D point clouds is essential. The presented algorithm is
designed to be highly parallelizable and can be implemented on modern GPUs for fast execution. The com-
putation is based on a convolution of a voxel based representation of the point cloud and a voxelized integral
volume. The generation of the voxel-based representation neither requires additional surface information or
normals nor needs to approximate them. The proposed approach is robust against noise up to the mean distance
between the 3-D points. In addition, the algorithm provides moderate scale invariance, i. e., it can approximate
keypoints for lower resolution versions of the input point cloud. This is particularly useful, if keypoints are
supposed to be used with any local 3-D point cloud descriptor to recognize or classify point clouds at different
scales. We evaluate our approach in a direct comparison with state-of-the-art keypoint detection algorithms in
terms of repeatability and computation time.
1 INTRODUCTION
3-D object recognition and classification is a funda-
mental part of computer vision research. Many of the
existing recognition systems use local feature based
methods as they are more robust to occlusion and clut-
ter. In those systems keypoint detection should be the
first major step to get distinctive local areas for dis-
criminative local feature descriptions. But a recent
survey on feature based 3-D object recognition sys-
tems (Guo et al., 2014) shows, that many major sys-
tems for local feature based 3-D object recognition
use sparse sampling or mesh decimation methods to
create a set of points on which the feature descriptors
will be computed. In terms of repeatability and in-
formativeness these methods do not result in qualified
3-D keypoints.
There are a variety of reasons why existing 3-D
keypoint detection algorithms are not used: Some of
them are sensitive to noise and some are time consum-
ing. Furthermore, there is only a handful of meth-
ods, that work with unstructured 3-D point clouds
without a time consuming approximation of local sur-
face patches or normal vectors (Pauly et al., 2003;
Matei et al., 2006; Flint et al., 2007; Unnikrishnan
and Hebert, 2008; Zhong, 2009; Mian et al., 2010).
This paper addresses the problems described
above. The proposed method is a fast and robust algo-
rithm for automatic identification of 3-D keypoints in
unstructured 3-D point clouds. We create a filled and
watertight voxel representation (in terms of a dense
voxel connectivity) of a point cloud. This voxel rep-
resentation is convolved with a spherical convolution
kernel. The sphere works as an integral operator on all
voxels containing points of the point cloud. The con-
volution gives the proportion of voxels of the sphere
which are inside the point cloud. The proportion val-
ues are used to identify regions of interest, and from
these robust keypoints are extracted. All parts of
the algorithm are highly parallelized and thus will be
computed very quickly. The size of the convolution
kernel can be adopted to the size of the area which is
used by the local feature descriptor. Furthermore, we
can easily simulate a lower resolution point cloud by
increasing the voxel size. Therefore, we can create
keypoints for multiple resolutions. Finally we will
show, that our approach provides robust keypoints,
even if we add noise to the point cloud.
2 RELATED WORK
There are many 3-D keypoint detection algorithms
131
Garstka J. and Peters G..
Fast and Robust Keypoint Detection in Unstructured 3-D Point Clouds.
DOI: 10.5220/0005569501310140
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 131-140
ISBN: 978-989-758-123-6
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

that work on meshes or use surface reconstruction
methods. A brief overview is given in a recent sur-
vey paper (Guo et al., 2014). But there are only a few
of them that work directly on unstructured 3-D point
cloud data. They have been compared multiple times
(Salti et al., 2011; Dutagaci et al., 2012; Filipe and
Alexandre, 2013) and therefore, we will give just a
short overview of algorithms, which are designed to
work with point clouds only.
(Pauly et al., 2003) use a principal component
analysis to compute a covariance matrix C for the lo-
cal neighborhood of each point p. With the eigen-
values λ
1
, λ
2
and λ
3
they introduce the surface vari-
ation σ
n
(p) = λ
1
/(λ
1
+ λ
2
+ λ
3
), for a neighborhood
of size n, i. e., the n nearest neighbors to p. Within a
smoothed map of surface variations Pauly et al. do a
local maxima search to find the keypoints. A major
drawback of this method is, that the surface variation
is sensitive to noise (Guo et al., 2014).
(Matei et al., 2006) use a similar approach as
Pauly et al., but they use only the smallest eigenvalue
λ
3
of the covariance matrix C for a local neighbor-
hood of a point p to determine the surface variation.
But in contrast to Pauly et al., the method from Matei
et al. provides only a fixed-scale keypoint detection.
The algorithm presented by (Flint et al., 2007) is
a 3-D extension of 2-D algorithms like SIFT (Lowe,
2004) and SURF (Bay et al., 2006) called THRIFT.
They divide the spatial space by a uniform voxel grid
and calculate a normalized quantity D for each voxel.
To construct a density scale-space Flint et al. convolve
D with a series of 3-D Gaussian kernels g(σ). This
gives rise to a scale-space S(p,σ) = (D ⊗g(σ))(p)
for each 3-D point p. Finally, they compute the de-
terminant of Hessian matrix at each point of the scale
space. Within the resulting 3 ×3 ×3 ×3 matrix, a
non maximal suppression reduces the entries to local
maxima, which become interest points.
(Unnikrishnan and Hebert, 2008) introduce a 3-D
keypoint detection algorithm based on an integral op-
erator for point clouds, which captures surface vari-
ations. The surface variations are determined by an
exponential damped displacement of the points along
the normal vectors weighted by the mean curvature.
The difference between the original points and the
displaced points are the surface variations which will
be used to extract the 3-D keypoints, i. e., if a dis-
placement is an extremum within the geodesic neigh-
borhood the corresponding 3-D point is used as key-
point.
(Zhong, 2009) propose another surface variation
method. In their work they use the ratio of two succes-
sive eigenvalues to discard keypoint candidates. This
is done, because two of the eigenvalues can become
equal and thus ambiguous, when the corresponding
local part of the point cloud is symmetric. Apart from
this, they use the smallest eigenvalue to extract 3-D
keypoints, as proposed by Matei et al.
Finally, also (Mian et al., 2010) propose a surface
variation method. For each point p they rotate the lo-
cal point cloud neighborhood in order to align its nor-
mal vector n
p
to the z-axis. To calculate the surface
variation they apply a principal component analysis to
the oriented point cloud and use the ratio between the
first two principal axes of the local surface as measure
to extract the 3-D keypoints.
3 OUR ALGORITHM
The basic concept of our algorithms is adopted from
a keypoint detection algorithm for 3-D surfaces in-
troduced by (Gelfand et al., 2005). To be able to
use an integral volume to calculate the inner part of
a sphere without structural information of the point
cloud, we designed a volumetric convolution of a wa-
tertight voxel representation of the point cloud and a
spherical convolution kernel. This convolution calcu-
lates the ratio between inner and outer voxels for all
voxels that contain at least one point of the 3-D point
cloud. The convolution values of the point cloud get
filled into a histogram. Keypoint candidates are 3-D
points with rare values, i. e., points corresponding to
histogram bins with a low level of filling. We clus-
ter these candidates, find the nearest neighbor of the
centroid for each cluster, and use these points as 3-D
keypoints.
Thus, our method for getting stable keypoints in
an unstructured 3-D point cloud primarily consists of
the following steps:
1. Estimate the point cloud resolution to get an ap-
propriate size for the voxel grid.
2. Transfer the point cloud to a watertight voxel rep-
resentation and fill all voxels inside of this water-
tight voxel model with values of 1.
3. Calculate a convolution with a voxel representa-
tion of a spherical convolution kernel.
4. For each 3-D point fill the convolution results of
its corresponding voxel into a histogram.
5. Cluster 3-D points with rare values, i. e., 3-D
points of less filled histogram bins, and use the
centroid of each cluster to get the nearest 3-D
point as stable keypoint.
The details of these steps are provided in the sections
below.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
132

3.1 Point Cloud Resolution
A common way to calculate a point cloud resolution
is to calculate the mean distance between each point
and its nearest neighbor. Since we use the point cloud
resolution to get an appropriate size for the voxel
grid (which is to be made watertight in the following
steps), we are looking for a voxel size which leads to
a voxel representation of the point cloud, where only
a few voxels corresponding to the surface of the ob-
ject remain empty, while as much as possible of the
structural information is preserved.
To get appropriate approximations of point cloud
resolutions, we carried out an experiment on datasets
obtained from ’The Stanford 3-D Scanning Reposi-
tory’ (Stanford, 2014). We examined the mean Eu-
clidean distances between n nearest neighbors of m
randomly selected 3-D points, with n ∈ [2,10] and
m ∈ [1,100]. The relative difference between the
number of voxels based on the 3-D points to the num-
ber of voxels based on the triangle mesh were filled
into a separate histogram for each value of n. The his-
togram of the ’Stanford Bunny’ shown in figure 1 is
illustrative for all results.
Figure 1: The quality of the voxel grid based on the point
cloud resolution calculated by the mean of n = 7 nearest
neighbors. The x-axis shows the relative difference between
the number of voxels based on the 3-D points to the number
of voxels based on the triangle mesh of ’Stanford Bunny’.
The y-axis shows the number of randomly selected points
which have been used to calculate the values.
With n = 7 the absolute mean of the relative dif-
ference is at a minimum. Thus, the experiments us-
ing different 3-D objects show that an approximated
point cloud resolution with the use of 7 nearest neigh-
bors and with a sample size of 50 randomly selected
points is a good choice to get a densely filled initial
voxel grid within a small computation time.
3.2 Fast Creation of a Watertight
3-D Model
Initially we create a voxel grid of cubic voxels with
an edge length of the point cloud resolution as de-
scribed above. Each voxel containing a 3-D point is
initialized with a value of 1.0. This creates an approx-
imated voxel representation of the surface. The voxels
representing the point cloud are defined as watertight,
if the voxels result in a densely connected structure
without gaps.
To be able to fill inner values of objects, we as-
sume that it is known whether the point cloud repre-
sents a closed model or a depth scan, which has its
depth direction along the z-axis.
In case of a depth scan, which is very common
in robotics, we take the maximum depth value z
max
and the radius of the convolution kernel r
conv
, and set
the value of all voxels along the z-axis beginning with
the first voxel with a value of 1 (a surface voxel) and
ending with depth of at least z
max
+ r
conv
to a value of
1, too. An illustration of this can be seen in figure 2.
Figure 2: This is a voxel representation of a view dependent
patch (depth scan) from the ’Bunny’. Blue dots represent
voxels corresponding to 3-D points. Red dots represent the
filled voxels below the surface.
In case we assume a closed model we have to fill
all inner voxels. Due to variations in density of the
point cloud and the desire to keep the voxel size as
small as possible, it often occurs that the voxel surface
is not watertight. For first tests we implemented two
different approaches to close holes in the voxel grid.
The first implementation was based on the method
from (Adamson and Alexa, 2003). Their approach
is in fact intended to enable a ray tracing of a point
cloud. They use spheres around all points of the point
cloud to dilate the points to a closed surface. Shooting
rays through this surface can be used to close holes.
The second implementation was based on a method
by (Hornung and Kobbelt, 2006). Their method cre-
ates a watertight model with a combination of adap-
tive voxel scales and local triangulations. Both meth-
ods create watertight models without normal estima-
tion. But the major drawback of both methods con-
sists in their long computation times.
Since the method we propose should be fast, these
FastandRobustKeypointDetectioninUnstructured3-DPointClouds
133
concepts were discarded for our approach. Instead we
use a straightforward solution, which appears to be
sufficient for good but fast results. The filling of the
voxel grid is described exemplary for the one direc-
tion. The calculation of the other directions is per-
formed analogously.
Let u, v and w the indexes of the 3-D voxel grid in
each dimension. For each pair (u,v) we iterate along
all voxels in w-direction. Beginning with the first oc-
currence of a surface voxel (with a value of 1) we
mark all inner voxels by adding −1 to the subsequent
voxels until we reach the next surface voxel. These
steps are repeated until we reach the w boundary of
the voxel grid. If we added a value of −1 to the last
voxel, we must have passed a surface through a hole.
In this case we need to reset all values for (u, v) back
to the previous values.
After we did this for each dimension, all voxels
with a value ≤ −2, i. e., all voxel which have been
marked as inner voxels by passes for at least two di-
mensions, will be treated as inner voxels and their
value will be set to a value of 1. All other voxels will
get a value of 0.
We already mentioned, that, if we pass the surface
through a hole, we set back all voxel values to previ-
ous values. This might result in tubes with a width of
one voxel (see figure 3(a)). Because of that, we fill
these tubes iteratively in a post-processing step, with
the following rule:
If a voxel at position (u,v,w) has a value of 0 and
at least each of the 26 neighbor voxels except of one
of the six direct neighbors (u ±1 or v ±1 or w ±1)
has a value of 0, the voxel at (u,v, w) gets a value of
1, too. The result is shown in figure 3(b).
3.3 Convolution
The convolution is done with a voxelized sphere of
radius r
conv
. For a fast GPU based implementation
we use the NVIDIA FFT-implementation cuFFT. Fig-
ure 4(a) and figure 4(b) visualize the results showing
those voxels which contain 3-D points from the ini-
tial point cloud. The convolution values are in [0,1].
While values near 0 are depicted red, values near 1
are depicted blue to purple, and values of about 0.5
are depicted green.
3.4 Histograms
Following the computation of the convolution, we
have to identify all convolution values which are in-
teresting, i. e., which are less frequent. To find those
regions of values which are less frequent, we fill the
convolution values into a histogram. To get an appro-
(a) (b)
Figure 3: This figures shows sliced versions of the filled
voxel grid of the ’Bunny’. All inner voxels get filled after
the surface is passed. This is done for each direction u, v and
w. If the surface gets missed through a hole, it might lead
to tubes with a width of one voxel as shown in subfigure
(a). If we post-process this voxel grid, we can identify and
fill those tubes. This leads to a nearly complete filled voxel
grid as shown in subfigure (b).
(a) (b)
Figure 4: The two subfigures show colored convolution re-
sults of the ’Bunny’ in full resolution using a convolution
kernel of radius r
conv
= 10pcr (pcr = point cloud resolu-
tion). Subfigure (a) shows a depth scan (pcr = 0.00167)
with convolution values between 0.23 (red) and 0.79 (blue)
while subfigure (b) shows the closed point cloud (pcr =
0.00150) with values between 0.08 (red) and 0.83 (blue).
priate amount of bins we use Scott’s rule (Scott, 1979)
to get a bin width b:
b =
3.49σ
3
√
N
, (1)
where σ is the standard deviation of N values.
In case of a depth scan we need to take into ac-
count that the convolution values at outer margins do
not show the correct values. Thus, we ignore all val-
ues of points within an outer margin r
conv
.
3.5 Clustering
From the histogram we select all bins filled with val-
ues of at most 1% of all points. It turned out that this
is a good choice for an upper limit since higher values
lead to large clusters. On the other hand, a significant
smaller limit leads to fragmented and unstable clus-
ters.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
134

All points corresponding to the values in the se-
lected bins will be used as keypoint candidates for
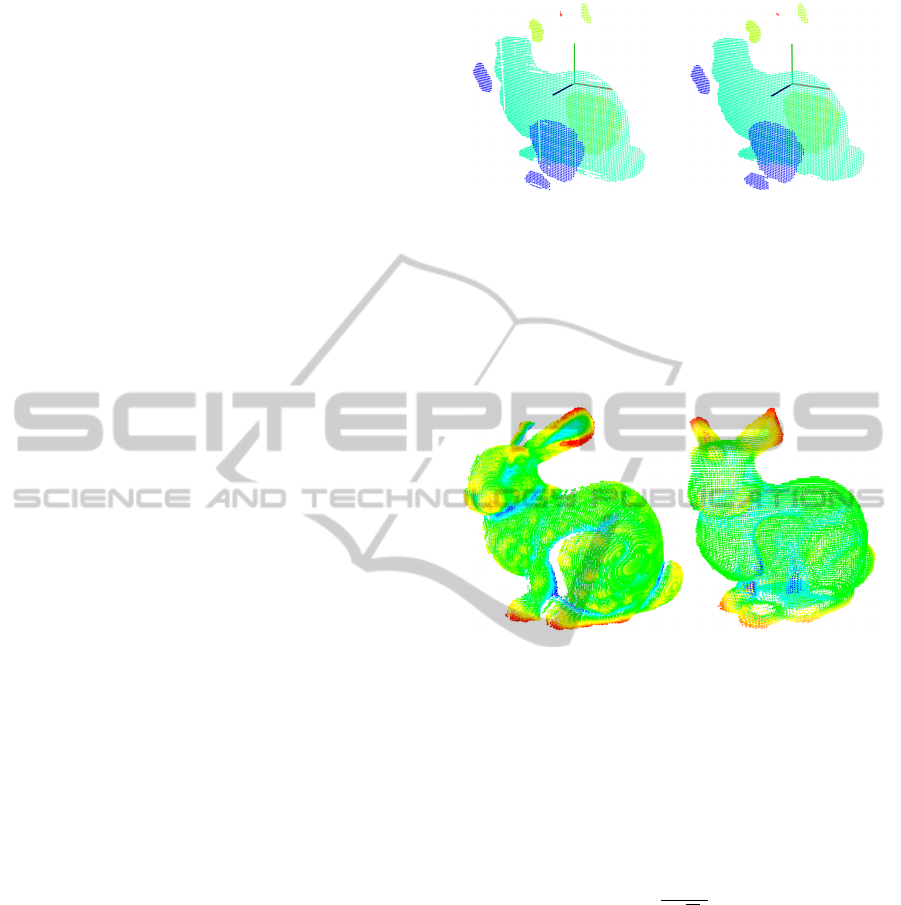
clustering. Figure 5(a) shows all keypoint candidates
for the ’Bunny’. We cluster these points using the
Euclidean distance with a range limit of 3pcr. This
enables us to handle small primarily longish clusters,
e. g., the region above the bunny’s hind legs, as a sin-
gle connected cluster. Figure 5(b) illustrates the dif-
ferent clusters with separate colors.
For each cluster we calculate the centroid. Each
centroid is used to find its nearest neighbor among the
3-D points of the corresponding cluster. This nearest
neighbor is used as 3-D keypoint. Figure 5(c) and
figure 5(d) show the results for the ’Bunny’.
(a) (b)
(c) (d)
Figure 5: These subfigures illustrate the process of obtain-
ing clusters and keypoints from the set of possible can-
didates. Subfigure (a) shows all 3-D keypoint candidates
(blue) for the ’Bunny’. Subfigure (b) shows all clusters
found for an Euclidean distance with a range limit of 3pcr.
Subfigure (c) shows a combination of colorized clusters and
the corresponding 3-D keypoints. Finally, subfigure (d)
shows the isolated keypoints.
4 RESULTS
We evaluated our results with respect to the two main
quality features repeatability and computation time.
To be comparable to other approaches we used the
same method of comparing different keypoint detec-
tion algorithms and the same dataset as described by
(Filipe and Alexandre, 2013), i.e., we used the large-
scale hierarchical multi-view RGB-D object dataset
from Lai et al. (Lai et al., 2011a). The dataset con-
tains over 200000 point clouds from 300 distinct ob-
jects. The point clouds have been collected using a
turntable and an RGB-D camera. More details can be
found in another article by (Lai et al., 2011b).
4.1 Repeatability under Rotation
(Filipe and Alexandre, 2013) use two different mea-
sures to compare the repeatability: the relative and
absolute repeatability. The relative repeatability is the
proportion of keypoints determined from the rotated
point cloud, that fall into a neighborhood of a key-
point of the reference point cloud. The absolute re-
peatability is the absolute number of keypoints deter-
mined in the same manner as the relative repeatability.
To compute the relative and absolute repeatabil-
ity, we randomly selected five object classes (’cap’,
’greens’, ’kleenex’, ’scissor’, and ’stapler’) and
picked 10 point clouds within each object class ran-
domly as well. Additionally, these 50 base point
clouds were rotated around random axes at angles of
5
◦
, 15
◦
, 25
◦
, and 35
◦
. Afterwards, we applied our al-
gorithm on each of these 250 point clouds. For neigh-
borhood sizes n from 0.00 to 0.02 in steps of 0.001
the keypoints of the rotated point clouds were com-
pared with the keypoints of the base point clouds. If a
keypoint of a rotated point cloud fell within a neigh-
borhood n of a keypoint of the base point cloud, the
keypoint was counted. Finally, the absolute repeata-
bility was determined based on these counts for each
n as an average of the 50 corresponding point clouds
for each angle. The relative repeatability rates are the
relations between the absolute repeatabilities of the
rotated point clouds and the number of keypoints of
the base point clouds.
Figure 6 opposes relative repeatability rates of our
approach (left hand side) to the corresponding results
of four state-of-the-art keypoint detection algorithms
(right hand side). Figure 7 does the same for ab-
solute repeatability rates. The approaches evaluated
by (Filipe and Alexandre, 2013) are Harris3D (Sipi-
ran and Bustos, 2011), SIFT3D (Flint et al., 2007),
ISS3D (Zhong, 2009), and SUSAN (Smith and Brady,
1997) extended to 3-D by (Filipe and Alexandre,
2013).
In more detail, the graphs on the left of both fig-
ures 6 and 7 show the average relative, resp. abso-
lute, repeatability of keypoints computed with our al-
gorithm for 5 randomly selected objects over 10 itera-
tions, i. e., with 10 different rotation axes. The graphs
FastandRobustKeypointDetectioninUnstructured3-DPointClouds
135

(a) Relative repeatability of keypoints at a rotation angle of 5
◦
.
(b) Relative repeatability of keypoints at a rotation angle of 15
◦
.
(c) Relative repeatability of keypoints at a rotation angle of 25
◦
.
(d) Relative repeatability of keypoints at a rotation angle of 35
◦
.
Figure 6: Relative repeatability. Left: Our approach. Right: Four state-of-the-art approaches, diagrams taken from the
evaluation done by (Filipe and Alexandre, 2013).
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
136
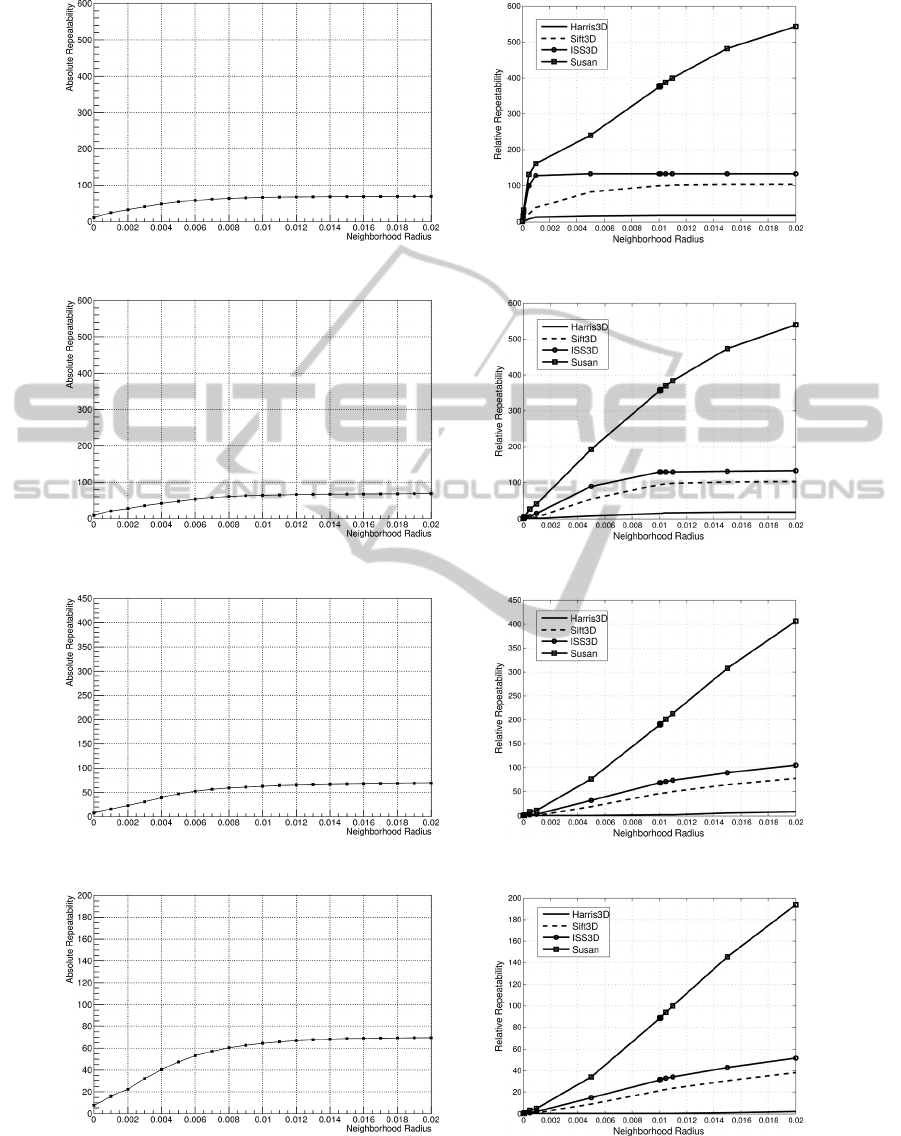
(a) Absolute repeatability of keypoints at a rotation angle of 5
◦
.
(b) Absolute repeatability of keypoints at a rotation angle of 15
◦
.
(c) Absolute repeatability of keypoints at a rotation angle of 25
◦
.
(d) Absolute repeatability of keypoints at a rotation angle of 35
◦
.
Figure 7: Absolute repeatability. Left: Our approach. Right: Four state-of-the-art approaches, diagrams taken from the
evaluation done by (Filipe and Alexandre, 2013). Note: The diagrams taken from Filipe and Alexandre have wrong axis
labels. However, they contain the absolute repeatability of keypoints.
FastandRobustKeypointDetectioninUnstructured3-DPointClouds
137
(a) Repeatability for a point cloud with 0.5pcr additional random noise at a rotation angle of 5
◦
.
(b) Repeatability for a point cloud with 0.5pcr additional random noise at a rotation angle of 15
◦
.
Figure 8: Our approach with additional noise. Left: Relative repeatability. Right: Absolute repeatability.
on the right of both figures are taken from the evalua-
tion done by (Filipe and Alexandre, 2013).
It is striking, that the relative repeatability rates
of our approach are considerably higher for large ro-
tation angles than those of all other state-of-the-art
approaches that have been compared by Filipe and
Alexandre. Only for an rotation angle of 5
◦
one of
the other algorithms (ISS3D) is able to outperform
our approach significantly in the range of small neigh-
borhood radii. On the other hand, the results of our
algorithm in terms of absolute repeatability of key-
points are in general less convincing, although for all
of the condsidered rotation angles it outperforms one
of the other approaches (Harris3D). For a rotation an-
gle of 35
◦
our algorithm outperformes even three of
the other approaches considered (Harris3D, SIFT3D,
and ISS3D).
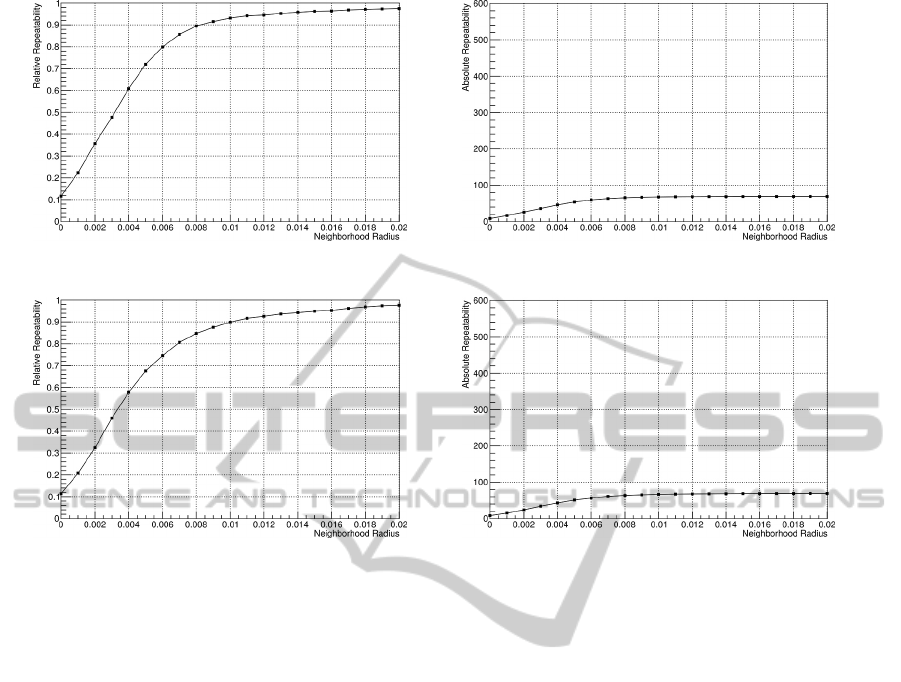
4.2 Repeatability under Noise
Furthermore, we have repeated the described simula-
tions for point clouds with additional random noise
at a level of 0.5 times of the point cloud resolution.
The graphs of figure 8 display the average repeatabil-
ity rates (relative and absolute) for point clouds with
added noise. The differences between these curves
and their corresponding curves from the simulations
without noise are negligible, which shows that our ap-
proach is able to cope with a fair amount of noise, as
well.
4.3 Computation Time
To calculate average computation times we computed
the 3-D keypoints 10 times for each point cloud. The
system configuration we used for all experiments is
given in table 1. The computation time of our al-
gorithm correlates with the number of voxels, i. e.,
with the dimensions of the voxel grids, which must be
powers of two. Measured average computation times
in dependence of voxel grid dimensions are given in
table 2.
The computation time for most of the point clouds
was below 1s. For many of the point clouds the com-
putation time fell within a range below 300ms. The
average computation time for all 250 point clouds
which were used to compare the repeatability rates
was 457ms. This is considerably fast, especially in
comparison to the average computation times of Har-
ris3D (1010ms) and ISS3D (1197ms), which have
been determined on the same system.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
138

Table 1: System configuration for experiments.
System configuration
Processor: Intel Xeon E5630 @2.53GHz
Memory: 12 GB
GPU: NVIDIA GeForce GTX 670
GPU memory: 2 GB GDDR5
OS: Debian GNU/Linux
NVIDIA driver: 340.32
Table 2: Average computation times.
Voxel Grid Dimension Time
512 ×256 ×128 ≈ 1500ms
256 ×256 ×128 ≈ 700ms
256 ×256 ×64 ≈ 300ms
256 ×128 ×128 ≈ 350ms
256 ×128 ×64 ≈ 180ms
128 ×128 ×128 ≈ 200ms
128 ×128 ×64 ≈ 110ms
128 ×64 ×64 ≈ 60ms
64 ×64 ×64 ≈ 35ms
5 CONCLUSION
In this paper we have presented a fast and robust ap-
proach for extracting keypoints from an unstructured
3-D point cloud. The algorithm is highly paralleliz-
able and can be implemented on modern GPUs.
We have analyzed the performance of our ap-
proach in comparison to four state-of-the-art 3-D key-
point detection algorithms by comparing their results
on a number of 3-D objects from a large-scale hierar-
chical multi-view RGB-D object dataset.
Our approach has been proven to outperform other
3-D keypoint detection algorithms in terms of relative
repeatability of keypoints. Results in terms of abso-
lute repeatability rates are less significant. An impor-
tant advantage of our approach is its speed. We are
able to compute the 3-D keypoints within a time of
300ms for most of the tested objects.
Furthermore, the results show a stable behavior of
the keypoint detection algorithm even on point clouds
with added noise. Thus, our algorithm might be a
fast and more robust alternative for systems that use
sparse sampling or mesh decimation methods to cre-
ate a set of 3-D keypoints.
REFERENCES
Adamson, A. and Alexa, M. (2003). Ray tracing point
set surfaces. In Shape Modeling International, 2003,
pages 272–279. IEEE.
Bay, H., Tuytelaars, T., and Van Gool, L. (2006). Surf:
Speeded up robust features. In Computer Vision–
ECCV 2006, pages 404–417. Springer.
Dutagaci, H., Cheung, C. P., and Godil, A. (2012). Eval-
uation of 3d interest point detection techniques via
human-generated ground truth. The Visual Computer,
28(9):901–917.
Filipe, S. and Alexandre, L. A. (2013). A comparative eval-
uation of 3d keypoint detectors. In 9th Conference on
Telecommunications, Conftele 2013, pages 145–148,
Castelo Branco, Portugal.
Flint, A., Dick, A., and Hengel, A. v. d. (2007). Thrift: Lo-
cal 3d structure recognition. In Digital Image Comput-
ing Techniques and Applications, 9th Biennial Confer-
ence of the Australian Pattern Recognition Society on,
pages 182–188. IEEE.
Gelfand, N., Mitra, N. J., Guibas, L. J., and Pottmann, H.
(2005). Robust global registration. In Symposium on
geometry processing, volume 2, page 5.
Guo, Y., Bennamoun, M., Sohel, F., Lu, M., and Wan,
J. (2014). 3d object recognition in cluttered scenes
with local surface features: A survey. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
99(PrePrints):1.
Hornung, A. and Kobbelt, L. (2006). Robust reconstruction
of watertight 3d models from non-uniformly sampled
point clouds without normal information. In Proceed-
ings of the Fourth Eurographics Symposium on Geom-
etry Processing, SGP ’06, pages 41–50, Aire-la-Ville,
Switzerland, Switzerland. Eurographics Association.
Lai, K., Bo, L., Ren, X., and Fox, D. (2011a). A large-
scale hierarchical multi-view rgb-d object dataset. In
Robotics and Automation (ICRA), 2011 IEEE Interna-
tional Conference on, pages 1817–1824. IEEE.
Lai, K., Bo, L., Ren, X., and Fox, D. (2011b). A scalable
tree-based approach for joint object and pose recogni-
tion. In AAAI.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International Journal of Com-
puter Vision, 60:91–110.
Matei, B., Shan, Y., Sawhney, H. S., Tan, Y., Kumar, R., Hu-
ber, D., and Hebert, M. (2006). Rapid object indexing
using locality sensitive hashing and joint 3d-signature
space estimation. Pattern Analysis and Machine Intel-
ligence, IEEE Transactions on, 28(7):1111–1126.
Mian, A., Bennamoun, M., and Owens, R. (2010). On the
repeatability and quality of keypoints for local feature-
based 3d object retrieval from cluttered scenes. In-
ternational Journal of Computer Vision, 89(2-3):348–
361.
Pauly, M., Keiser, R., and Gross, M. (2003). Multi-scale
feature extraction on point-sampled surfaces. In Com-
puter graphics forum, volume 22, pages 281–289. Wi-
ley Online Library.
Salti, S., Tombari, F., and Stefano, L. D. (2011). A per-
formance evaluation of 3d keypoint detectors. In
3D Imaging, Modeling, Processing, Visualization and
Transmission (3DIMPVT), 2011 International Con-
ference on, pages 236–243. IEEE.
FastandRobustKeypointDetectioninUnstructured3-DPointClouds
139

Scott, D. W. (1979). On optimal and data-based histograms.
Biometrika, 66(3):pp. 605–610.
Sipiran, I. and Bustos, B. (2011). Harris 3d: a robust exten-
sion of the harris operator for interest point detection
on 3d meshes. The Visual Computer, 27(11):963–976.
Smith, S. M. and Brady, J. M. (1997). Susana new approach
to low level image processing. International journal
of computer vision, 23(1):45–78.
Stanford (2014). The stanford 3d scanning repository.
http://graphics.stanford.edu/data/3Dscanrep/.
Unnikrishnan, R. and Hebert, M. (2008). Multi-scale in-
terest regions from unorganized point clouds. In
Computer Vision and Pattern Recognition Workshops,
2008. CVPRW’08. IEEE Computer Society Confer-
ence on, pages 1–8. IEEE.
Zhong, Y. (2009). Intrinsic shape signatures: A shape de-
scriptor for 3d object recognition. In Computer Vision
Workshops (ICCV Workshops), 2009 IEEE 12th Inter-
national Conference on, pages 689–696. IEEE.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
140
