Simulation and Analysis of the Signal Transmission in the Optical

Transmission Medium

Rastislav Róka and Filip Čertík

Institute of Telecommunications, Slovak University of Technology in Bratislava, Ilkovičova 3, Bratislava, Slovakia

Keywords: Optical Transmission Medium, Linear and Nonlinear Effects, Simulation Model.

Abstract: This paper presents a possible way for simulating a signal transmission in the optical transmission medium.

A main attention is focused on characteristics and analysis of linear and nonlinear effects that influence

optical signals transmitting in the environment of optical fibers. Simultaneously, functional blocks created

in the Matlab Simulink programming environment for particular effects are presented in the proposed

simulation model. At the same time, the paper present a simulation of the optical transmission system that

can include various modulation and encoding techniques utilized for the signal transmission. In addition,

a comparison of results from the proposed simulation model with measurements on real optical transmission

paths is introduced.

1 INTRODUCTION

Nowadays, an interest in the signal transmission

through optical fibers rapidly increases due to the

transmission bandwidth. Constructing new optical

transmission paths can be time consuming,

expensive and sometimes not available solution. In

the electric domain, utilizing new advanced signal

processing can lead to increasing of the transmission

capacity. Such solutions can be easily integrated.

With increasing of modulation rates, linear and

nonlinear influences on the transmitted optical signal

are growing and by this way additional bit errors in

information signals are generating. Therefore, it is

important to design and simulate the influence on

advanced signal processing techniques in the optical

transmission system with respect to its linear and

nonlinear effects. The simulation gives transmission

boundaries of each advanced signal processing

techniques for the designed optical system and

allows comparing all the solutions for the optical

system before deployment. The simulation allows

increasing the data rate and the transmission range

of deployed optical transmission system using

advanced signal processing techniques and allows

designing a new optical transmission system with

different optical fibers.

In (Ahmed, 2007), an optical link simulator was

designed like a platform on which the transmission

and optimization of communication systems could

be carried out. The simulator has been developed

under the Simulink environment in the form of

modules.

In (Del Río Bellisco, 2004), a software tool

developed for simulating of optical communication

systems was presented. The simulation allows

determination of the spectral and frequency

responses of particular blocks and the whole system.

The tool has been developed using the Matlab

programming environment.

The accurate determination of fiber

nonlinearities is an important issue in the design of

optical communication systems. In (Batagejl, 2002),

the need of knowing fiber non-linear coefficients in

global optical networks was presented.

First, basic characteristics of the optical fiber are

introduced. The paper presents created simulation

blocks in detail for each environmental effect in the

optical transmission medium. The analysis of effects

is shown on the transmission of noncoherent OOK

modulated signals via the standard single-mode

fiber. In the final part, the comparison of results

from simulation models with measured parameters

from the Ciena system is introduced.

219

Róka R. and

Certík F..

Simulation and Analysis of the Signal Transmission in the Optical Transmission Medium.

DOI: 10.5220/0005569602190226

In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),

pages 219-226

ISBN: 978-989-758-120-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 ANALYSIS OF THE OPTICAL

TRANSSMISION MEDIUM

Each optical fiber represents a transmission system,

which is frequency dependent. Pulse propagation

inside this transmission system can be described by

the nonlinear Schrödinger equation (NLSE), which

is derivate from Maxwell equations. From the NLSE

equation we can expresses effects in optical fibers

that can be classified as:

a) linear effects, which are wavelength

depended,

b) nonlinear effects, which are intensity

depended.

2.1 Linear Effects

Major impairments of optical signals transmitted via

optical fiber are mainly caused by linear effects - the

dispersion and the attenuation. The attenuation limits

power of optical signals and represents transmission

losses. In practical way, it is a power loss that

depends on a length of the transmission path. Total

signal attenuation a [dB] is defined for a particular

wavelength, which is defined by



log10

dBa



(1)

where P

is the input power and P

is the output

power.

The attenuation of optical fibers is mainly caused

by material absorption losses, radiation scattering

and by bending losses (Saleh and Teich, 1991).

Nowadays, optical transmission systems are able to

minimize impact of the attenuation by deploying

regenerators or all optical amplifiers like Raman or

EDFA amplifiers increasing the optical system

range. The attenuation block is a part of the

Stimulated Raman and Brillouin scattering block

shown in fig.10.

Another source of linear effects represents the

dispersion that causes broadening of optical pulses

in time and phase shifting of signals at the fiber end.

There are three dispersion types:

 modal dispersion,

 chromatic dispersion,

 polarization mode dispersion.

The mode dispersion occurs in multi-mode fibers

due to unequal propagation constants of different

modes. The paper focused on the single-mode fiber

SMF and long-haul transmission systems, so the

modal dispersion is not considered (Binh, 2010).

The chromatic dispersion CD is caused by

a different time of the spreading wave through the

fiber for different wavelengths and it depends on the

spectral width of the pulse. The CD influences the

transmission signal by broadening the optical pulse

in time and by phase shifting the signal phase

(Keiser, 2003). To characterize the CD effect, the

group velocity delay GVD parameter is measured.

The GVD represents the amount of the optical pulse

broadening. The relation between the phase shift and

the optical pulse broadening cause by CD is given

by two equations







(2)

GVD







(3)

where t is a time, φ represents phase and f

represents modulation frequency.

The CD effect simulation is based on equations (2)

and (3). The CD block generates GVD values that

broaden a propagating transmission signal and

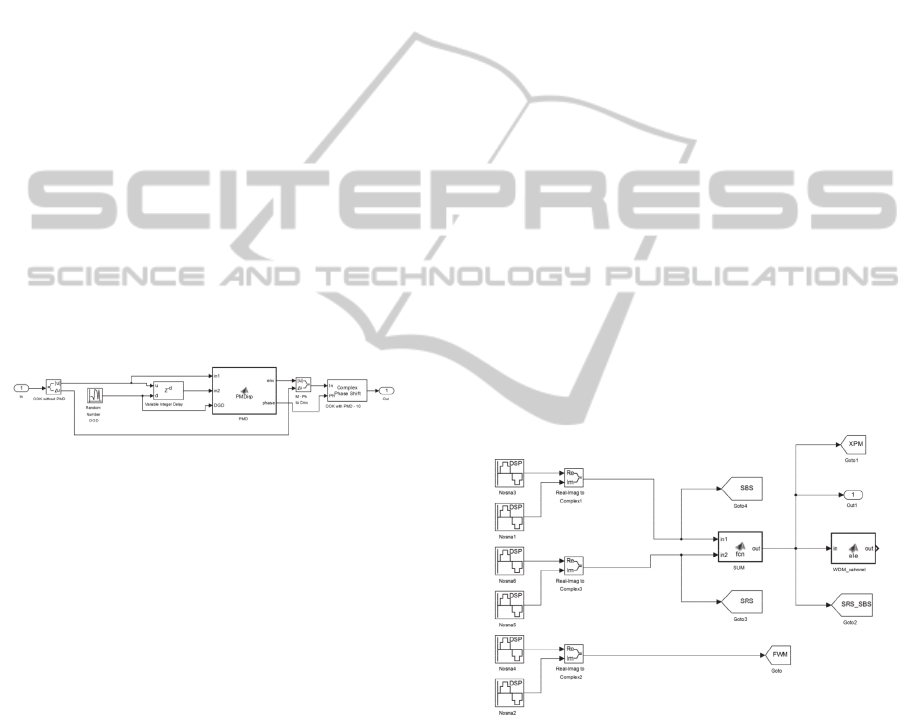
change its phase. The CD block is shown in fig.1

and consists of the GVD generator that adjusts the

variable integer delay using constant amplitude

representing the GVD. The delayed signal is created

with boundaries of the broadening. Both signals are

merged in the CD block, where a phase shift and

a power decrease are calculated. The output signal is

driven to the Complex phase shift block, where

a signal is shifted.

Figure 1: The CD block.

Another dispersion that occurs in the single-mode

fiber is called the polarization mode dispersion

PMD. The PMD is a random phenomenon that can

be only statistically evaluated. The light mode

transferred via the single mode optical fiber consists

of two modes on different polarization planes which

result from propagations principle states of

polarization PSP. In ideal optical fibers, two

polarization modes would propagate with the same

velocity. But in a reality, the optical fiber is

nonsymmetrical and imperfect and causes different

velocity of these two polarization modes. This effect

is also called the birefringence and it is equal to

differences Δn between relative refractive indexes

for ordinary n

and extraordinary n

rays given by

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

220

the equation

nnn

e 0





(4)

The group-delay difference between slow and fast

polarization modes is called the differential group

delay DGD measured in picoseconds. The DGD

between two orthogonal states of polarization SOP

causes the PMD. As a pulse propagates through

a light-wave transmission system with the PMD, the

pulse splits into fast and slow modes, and therefore

becomes broadened and changing the phase of

propagating pulse (Jamaludin, 2005).

The PMD effect simulation is similar to the CD

simulation. The PMD block is shown in fig.2 and is

based on equations (2) and (3). The difference is that

the PMD block uses the Random number generator

generating DGD values with the Gaussian

distribution. The PMD effect is negligible in

comparison with the CD and therefore we must

compensate the CD effect to highlight the PMD

effect on the transmitted signal. When the CD is

compensated, the high data rate signal can be

transmitted, where the PMD with its stochastically

behavior becomes more relevant and represents

boundaries for the transmission rate.

Figure 2: The PMD block.

2.2 Nonlinear Effects

These nonlinear effects play an important role in the

long haul optical signal transmission. We can

classify nonlinear effects by following way:

 Kerr nonlinearities are self-induced effects,

where the phase velocity of the pulse depending on

the pulse’s own intensity. The Kerr effect describes

a change in the fiber refractive index due to

electrical perturbations. Due to the Kerr effect, we

are able to describe FWM, SPM and XPM effects,

 Scattering nonlinearities occur due to a photon

inelastic scattering to lower energy photons. The

pulse energy is transferred to another wave with

a different wavelength.

2.2.1 The Four-wave Mixing Effect

The four-wave mixing FWM effect represents

a parametric interaction among waves satisfying

a particular phase relationship called the phase

matching. This nonlinear effect occurs only in

systems that carry more wavelengths through the

optical fiber and it is classified as a third-order

distortion phenomenon. The interaction between

waves generate the fourth wave that with angular

frequency ω

given by

321





(5)

The nonlinear interaction generates new frequency

components of the material polarization vector,

which can interfere with input fields if a phase

matching condition is obtain. The most frequency

components fall away from our original bandwidth

or near it. Frequency components that directly

overlap with bandwidth will cause an interference

with original waves (Singh, 2007). The power of

new generated waves can be obtain by solving

coupled propagation equations of four interacting

waves, which leads to equation (6) that mainly

depends on the power of neighbor channels, the

channel spacing and on the dispersion.

AAALdA

eek









2222

(6)

where factor η is the FWM efficiency, γ is the

nonlinear coefficient, L

is the effective length,

(z), A

(z) are powers of input waves, l is

the fiber length, α is the attenuation and d

the so-

called degeneracy factor (equal to 3 if the

degenerative FWM is considered, 6 otherwise).

Figure 3: The block scheme for generating additional

wavelength channels.

The block design for the FWM effect requires

the WDM technology and thus the generation of

additional wavelength channels. The data signal

generation of additional wavelength channels is

shown in fig.3. The additional neighbor channels are

mixed in the WDM block and driven to the FWM

block, which is shown in fig.4. The block scheme

first verifies the phase matching conditions and then

mixes the neighbor signals using the equation (6) if

phase conditions are satisfied.

SimulationandAnalysisoftheSignalTransmissionintheOpticalTransmissionMedium

221

Figure 4: The FWM block.

2.2.2 Self-phase and Cross-phase

Modulation Effects

The self-phase modulation SPM and the cross-phase

modulation XPM effects have an important impact

on high data speed communication systems that use

the dense wavelength division multiplexing DWDM.

The SPM effect occurs due to Kerr effect in which

the refractive index of optical fiber increases with

the optical intensity decreasing the propagation

speed and thus inducts the nonlinear phase shift. The

XPM effect is very similar to the SPM in which the

intensity from different wavelength channels

changes the signal phase and thus the XPM occurs

only in WDM systems. In fact, the XPM converts

power fluctuations in a particular wavelength

channel to phase fluctuations in other co-

propagating channels (Iannone, 1998). Both, SPM

and XPM effects results to spectral broadening and

distortion of the pulse shape, where spectral

broadening can be described by equation (7) and

phase shift by equation (8).







(7)

where ω' is the signal frequency influenced with the

SPM effect, ω

is the initial signal frequency

 





























(8)

where the first term in bracket represents the SPM

effect and the second term represents XPM effect.

In the equation (8), the factor 2 has its origin in

a form of the nonlinear susceptibility and represents

the XPM twice as effective as the SPM for the same

power amount. The XPM effect affects the signal

only the interacting signals superimpose in

time (Yasser, 2012). The XPM effect can decrease

a system performance even greater than the XPM

effect, especially in case of 100 channel systems.

The design of the SPM and XPM block is shown

in fig.5, where the SPM&XPM block calculates the

amount of spectral broadening using the equation

(8). Both outputs are driven to the Frequency

Shifting block, where the signal is spectrally

broaden.

Figure 5: The SPM & XPM block.

2.2.3 Stimulated Raman and Stimulated

Brillouin Scattering Effects

The Stimulated Brillouin Scattering SBS and

Stimulated Raman Scattering SRS effects influence

the intensity of the transmitted signal. In the SBS

case, the acoustic wave changes the frequency of

several photons that results to interference with

a transmitted signal. This frequency shifted wave is

propagating only in the opposite direction as the

transmitted signal and the power can be described by

ssspB

IIIg





(9)

where the I

is a pump signal, I

represent

transmitted signal intensity, g

is stimulated Raman

gain coefficient and α

and α

are losses of signals.

The SRS effect is similar to the SBS, were the

spectral width is wide and interferes with several

transmitted signals. The SRS effect propagates in

both directions (Cotter, 1993). Both stimulated

scattering effects represent a noise in optical

transmission systems. The power of the frequency

shifted wave can be described by

ssspR

IIIg





(10)

where the I

is a pump signal, I

represent

transmitted signal intensity, g

is stimulated Raman

gain coefficient and α

and α

are losses of signals.

The SRS&SBS block can be designed by adding

additional signal channels using a combination of

two equations. The equations include the transmitted

signal attenuation coefficients and therefore we can

design the common SRS&SBS and attenuation

block. The final block is shown in fig.6. Assuming

the SM fiber, the SRS downshifts the neighbor

signals by about 13,2 THz with the Raman band

around 5 THz and the SBS downshifts about 11 GHz

with the Brillouin band less than 20 MHz.

Figure 6: The SRS, SBS and attenuation block.

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

222

2.2.4 Modelling of Transmission Signals

Influenced Bynonlinear Effects

Following figures are displaying graphical

presentations of transmitted signals that are

influenced by nonlinear effects in the optical

transmission medium. The comparison of signals

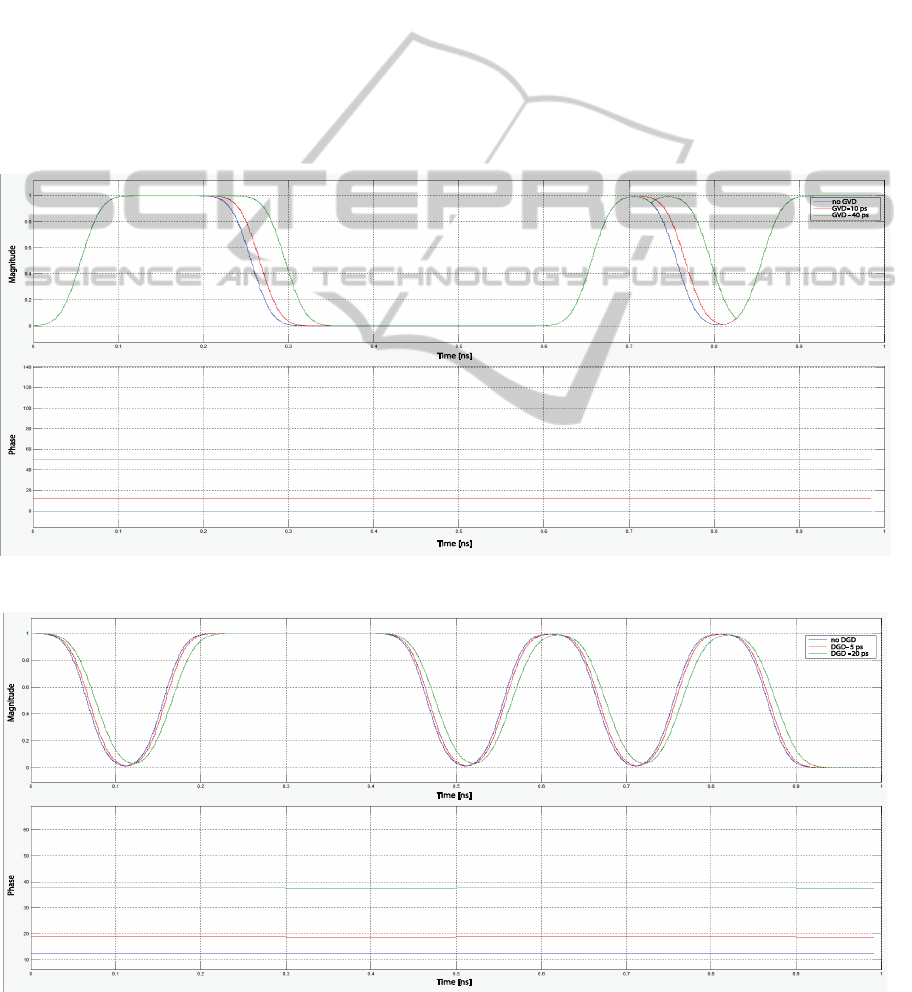
without and with the CD influence is shown in fig.7.

The PMD influence on a transmitted signal is shown

in fig.8. The FWM influence on the amplitude of

a transmitted signal is shown in fig.9. The fig.10

shows the signal phase shift due to phase modulation

effects. The SRS and SBS influences on

a transmitted signal with the attenuation are shown

in fig.11.

3 SIMULATION OF THE

OPTICAL TRANSMISSION

SYSTEM

The presented simulation model comes out from the

simulation model for optical communications

introduced in (Róka, 2012) (Róka and Čertík, 2014).

A modeling is performed in the Matlab Simulink

2014. The simulation model presents an influence of

linear and nonlinear effects at the signal

transmission in the optical transmission media. To

verify simulation model, we have prepared

a comparison of two optical transmission paths

measured in cooperation with the company Orange

Slovakia. The optical path_1 consists of the 59.2 km

standard SM fiber (ITU-T G.652) with the 10 Gb/s

Figure 7: The CD influence on a transmitted signal.

Figure 8: The PMD influence on a transmitted signal.

SimulationandAnalysisoftheSignalTransmissionintheOpticalTransmissionMedium

223

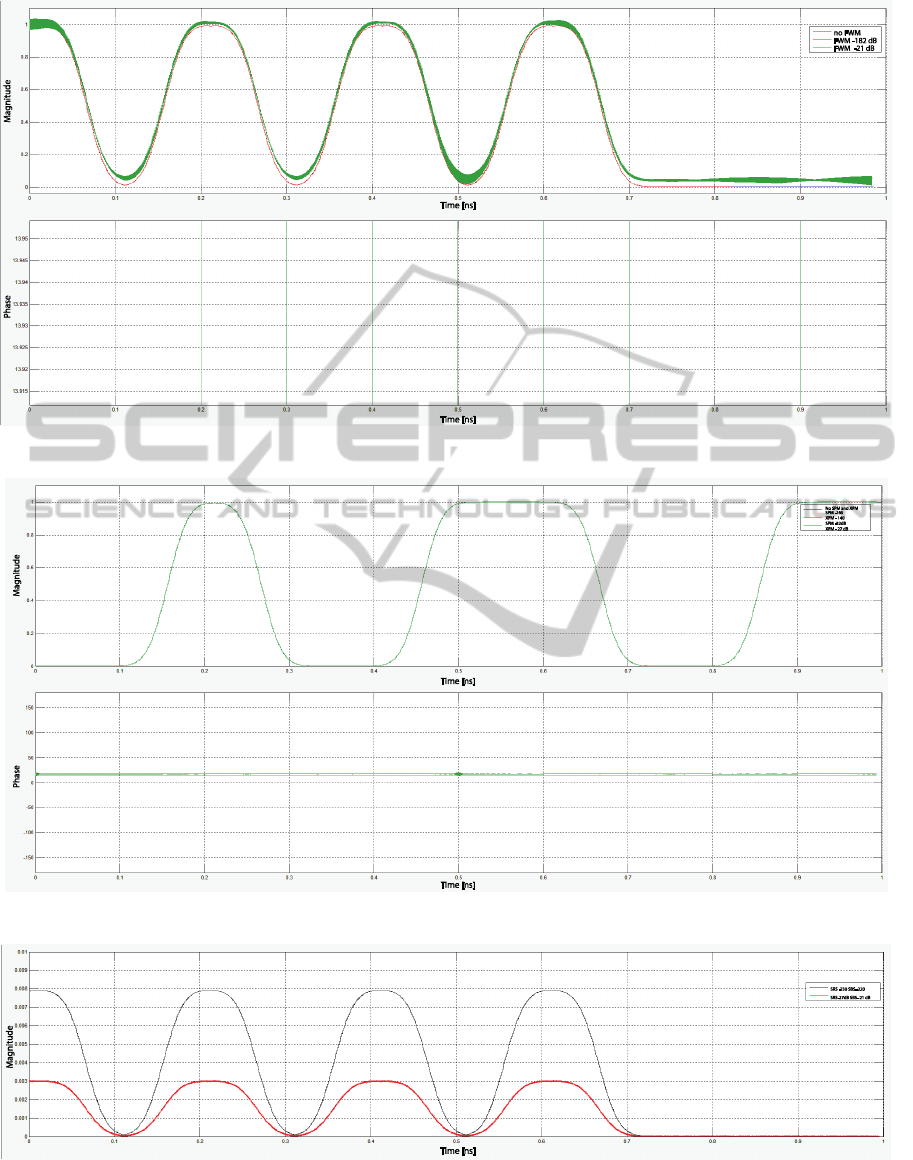
Figure 9: The FWM influence on a transmitted signal.

Figure 10: The SPM and XPM influences on a transmitted signal with the phase shift.

Figure 11: The SRS and SBS influences on a transmitted signal with the generated noise.

noncoherent OOK modulated signal using 80

channels. The optical path_2 consists of 170,7 km

standard SM (ITU-T G.652) fiber with 10 Gb/s

noncoherent OOK modulated signal using 80

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

224

channels. We examine the transmitted signal with

the frequency 193,4 THz. The path_1 is using only

one the erbium doped fiber amplifier EDFA at the

fiber end, while the path_2 is using additional 3

EDFA amplifiers every 40 km. The simulation

model for the path_1 is shown in fig.12 and the

simulation model for the path_2 is shown in fig 13.

For describing the signal transmission in the

optical transmission medium, we can calculate a bit

error rate parameter BER. The BER calculation for

each simulation model is done by comparing input

and output bits. The simulation results for the optical

path_1 and optical path_2 shows the BER parameter

higher than 10

-12

satisfying the transmission

condition. Both simulation models use the Reed-

Solomon Coding RS (255.239) that can enhance the

system BER parameter.

Figure 12: The optical path_1 simulation model.

Table 1: The comparison of the optical path_1 parameters.

Parameters Measured Simulated

Rx power

(dBm)

-13,2 -13,4

OSNR 25,9 24,3

PMD (ps) 1,06 1,25

SPM (dB) 0,87 1,22

XPM (dB) -57,59 -60,5

FWM (dB) N/A -124,3

Q 7,99 8,1

BER >10

-15

>10

-12

Figure 13: The optical path_2 simulation model.

Table 2: The comparison of the optical path_2 parameters.

Parameters Measured Simulated

Rx power

(dBm)

-13,69 -12,3

OSNR 21,07 20,9

PMD (ps) 1,74 1,83

SPM (dB) 1,03 1,1

XPM (dB) -42,02 -40,5

FWM (dB) N/A -112

Q 6,27 6,2

BER >10

-15

>10

-12

4 CONCLUSIONS

This contribution analyses linear and nonlinear

effects in the optical transmission medium. Using

created specific blocks in the Matlab Simulink, we

can simulate the influence of each optical fiber

effects on transmitted signals utilizing WDM optical

systems. We present results of the simulation for

the noncoherent OOK modulation signal

transmission in two different optical paths. Finally,

we compare analyzed results acquired from created

simulation models with measured parameters from

the real optical transmission paths.

5 FUTURE WORK

In future analysis, we can design a new combination

of high-bit rate coherent modulation formats, such as

QPSK, 8PSK, 16QAM and FSK, with different

encoding techniques, such as BCH, LDPC, for

analyzing and implementing in any optical

transmission systems.

ACKNOWLEDGEMENTS

This work is a part of research activities conducted

at Slovak University of Technology Bratislava,

Faculty of Electrical Engineering and Information

Technology, Institute of Telecommunications,

within the scope of the projects KEGA No. 039STU-

4/2013 “Utilization of Web-based Training and

Learning Systems at the Development of New

Educational Programs in the Area of Optical

Transmission Media”.

SimulationandAnalysisoftheSignalTransmissionintheOpticalTransmissionMedium

225

REFERENCES

Ahmed, G. H., Ali, O., 2007. Design and conception of

optical links simulator for telecommunication

applications under Simulink environment,

In: ELECTROSCIENCE 2007, pp.52-57, ISSN 1790-

5117.

Batagejl, B., 2002. Need of knowing non-linear coefficient

in optical networks, In: WSEAS 2002.

Binh L. N., 2010. Optical Fiber Communication Systems,

CRC Press.

Cotter D. 1993. Nonlinearity in optical fiber

communications, Springer Netherlands, Vol.49,

pp.322-362.

Del Río Bellisco, J., Alpuente Hermosilla, J., Sánchez

Montero, R., López Espí, P.L., 2004. Education tool

for optical communication engineering teaching,

In: WSEAS 2004.

Iannone E., Matera F., Mecozzi A., Settembre M., 1998.

Nonlinear Optical Communication Networks, John

Wiley and sons, pp.20-50, TK5103.59.N66.

Jamaludin Z., Abas A. F., Noor A. S. M., Abfullah M. K.,

2005. Issues in polarization mode dispersion (PMD)

for high speed fiber optics transmission. In: Suranaree

J. Sci. Technol., Vol. 12 No. 2.

Keiser G., 2003. Optical fiber communications, John

Wiley & Sons, Inc.

Róka R., 2012. Fixed Transmission Media. In: Technology

and Engineering Applications of Simulink, InTech,

Rijeka (Croatia).

Róka R., Čertík F., 2014. Simulation Tools for Broadband

Passive Optical Networks. In: Simulation

Technologies in Networking and Communications:

Selecting the Best Tool for the Test, CRC Press in

Taylor&Francis Group, Boca Raton (USA),

ISBN 978-1-4822-2549-5.

Saleh B. E. A., Teich M. C., 1991. Fundamentals of

photonics, Wiley-Interscience.

Singh S.P., Singh N., 2007. Nonlinear Effects in Optical

Fibers: Origin, Management and Applications. PIER

73, Progress In Electromagnetics Research, 249-275.

Yasser H. A., 2012. Polarization Losses in Optical Fibers.

In: Recent Progress in Optical Fiber Research,

InTech.

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

226