Application of Sliding Mode Control to the Ball and Plate Problem
David Debono and Marvin Bugeja
Department of Systems and Control Engineering, University of Malta, Msida MSD 2080, Malta
Keywords:
Ball and Plate System, Sliding Mode Control, Robust Control, Multivariable Control, Nonlinear Control.
Abstract:
This paper proposes and investigates the application of sliding mode control to the ball and plate problem.
The nonlinear properties of the ball and plate control system are first presented. Then the experimental setup
designed and built specifically for the purpose of this research is discussed. The paper then focuses on the im-
plementation and thorough evaluation of the experimental results obtained with two different control schemes:
the linear full-state feedback controller and the sliding mode controller. The latter control strategy was se-
lected for its robust and order reduction properties. Finally the control performance of the two controllers
is analysed. The sliding controller manages to obtain a faster and more accurate operation for continuously
changing reference inputs. The robustness of the proposed control scheme is also verified, since the system’s
performance is shown to be insensitive to parameter variations.
1 INTRODUCTION
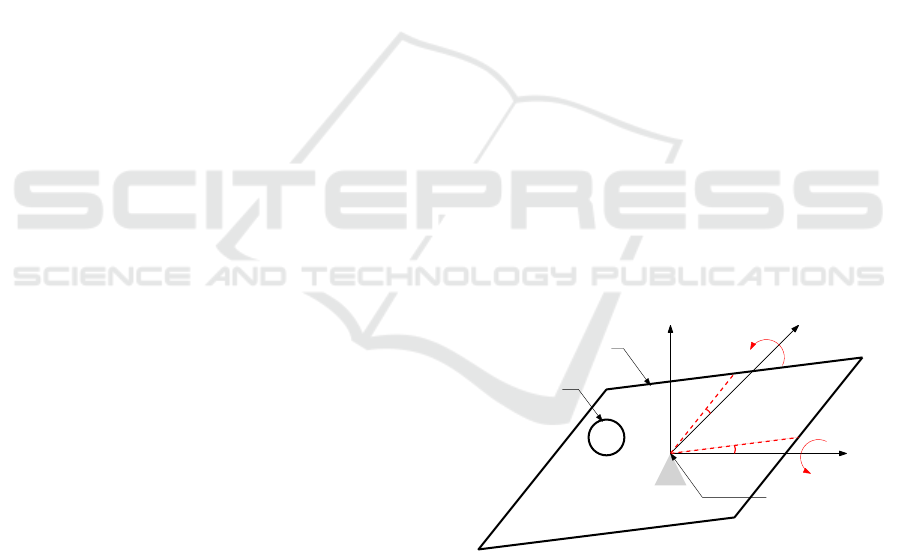
The ball and plate system, depicted in Figure 1, is one
of the most popular educational models developed
by control engineers to teach and validate various
control strategies. The control objective of the ball
and plate problem is to balance a ball, or to make
it track a desired trajectory, on a flat plate, solely
by tilting the plate relative to the horizontal plane.
This system is of particular interest to the control
community because it allows the user to study and
validate a wide class of both linear and nonlinear
control schemes, before applying them to real-life
applications that exhibit similar dynamics.
This control challenge, which reportedly originated
in the mid 1990s from Rockwell laboratory of
Czechoslovakia University, is an extension of the
traditional ball and beam system (Moarref et al.,
2008), (Wang et al., 2007), (Liu and Liang, 2010).
The ball and beam problem is a two degrees of
freedom (DOF) system whose objective is to stabilize
a rolling ball on a rigid beam. In contrast the ball
and plate system exhibits four DOF, namely the two
independent motions of the free rolling ball about the
plate’s plane and the two independent and orthogonal
inclinations of the plate which indirectly control the
ball’s motion. Since the system exhibits less actuators
than DOF, then it is clearly underactuated. Another
property of this setup is that it is a multiple-input
z
x
y
T
x
T
y
Q
x
Q
y
ball
Plate
Pivot
Figure 1: The ball and plate system.
multiple-output (MIMO) system, creating an interest-
ing situation where engineers can study and observe
the effects of cross-coupling between different inputs
and outputs. In addition the ball and plate setup is
also nonlinear and open-loop unstable. All these
properties lead to several control challenges that are
still being addressed by current research.
Throughout the years a variety of control topologies
have been applied to the ball and plate problem.
Awtar and Craig, in (Awtar et al., 2002), applied a
two-loop cascaded control strategy where the inner
loop controlled the plate’s actuation mechanism
and the outer loop controlled the ball dynamics of
the system. The response of the inner loop, for
such topologies, needs to appear instantaneous with
respect to the outer loop. The inner loop controller
consisted of a Proportional-Integral-Derivative (PID)
412
Debono D. and Bugeja M..
Application of Sliding Mode Control to the Ball and Plate Problem.
DOI: 10.5220/0005569804120419
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 412-419
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

servo controller while the ball dynamics were con-
trolled through a lead compensator. Similar linear
cascaded topologies like the linear full-state feedback
controller can also be used where the inner loop
usually consists of a digital torque controller while
standard LQR and pole-placement design procedures
are applied to the outer loop. Such linear topologies
manage to achieve a limited performance. This is due
to the unaccounted nonlinear dynamics that become
more dominant the further the states are from the
system’s equilibrium point. On the other hand in
(Moarref et al., 2008), (Wang et al., 2007) and (Yuan
and De-hu, 2009) the authors used a fuzzy estimator
in the outer loop to include some ”intelligence” in the
control action action used to regulate the ball position.
In (Ho et al., 2013) a standard linear full-state
feedback controller is used with the feedback lineari-
sation topology to control the ball and plate system.
Feedback linearisation techniques are subject to lim-
itations such as the undefined relative degree of the
linearised ball and plate system at certain locations.
The authors managed to apply an approximative
input-output feedback linearisation technique, where
higher terms of the output could be ignored. A
similar control topology that tries to force a nonlinear
system to behave like a linear system, is the recursive
backstepping method (Khalil, 2002). This method
has been successfully applied to regulate the ball’s
position of two different ball and plate setups in (Ker
et al., 2007) and (Hongrui et al., 2008). On the other
hand papers (Liu and Liang, 2010) and (Liu et al.,
2009) manage to successfully simulate different
sliding mode topologies on the ball and plate model.
Sliding mode control is a robust control strategy
that guarantees a suitable response even in the face
of model imprecisions and external disturbances.
Robustness is achieved by employing a discontinuous
control action. This paper focuses on the study,
comparison and experimental evaluation of this
robust control technique. In addition it presents the
design and construction of the physical ball and plate
experimental test-bed, designed and build specifically
for the purpose of such research.
Despite its interesting nonlinear properties, literature
indicates that the ball and plate system has not at-
tracted as much attention as other setups like the ball
and beam and the inverted pendulum experiments.
Recent works, like (Liu and Liang, 2010) and (Liu
et al., 2009), present the ball and plate results within
a simulation environment. According to Moarref
(Moarref et al., 2008), this is due to the structural
complexities involved in the ball and plate setup.
Papers (Moarref et al., 2008), (Awtar et al., 2002),
(Ker et al., 2007) present different mechanisms that
can be used to implement the actual ball and plate
system. The L-shaped mechanism presented in
(Awtar et al., 2002), is the most popular mechanical
structure, to transmit the necessary torques. In fact
this is the standard actuation mechanism used in
educational setups and research papers (Jadlovska
et al., 2009), (Wang et al., 2012). Variations of
the same mechanisms are presented in (Yuan and
De-hu, 2009),(Ker et al., 2007) and (Yuan and
Zhang, 2010) where different types of actuators
(pneumatic cylinders and magnetic levitation) are
used. The main limitation of such structures is the
resulting small angle plate deflections allowed by
the actuating mechanism. Moarref (Moarref et al.,
2008) presented a different actuation mechanism
where two stepper motors are located at the sides
of the plate. One of the motors is directly coupled
to a metal frame supporting the rotating plate. The
other motor is actuating the plate’s motion through
a mechanical linkage. This structure allows a larger
range of motion, but it is subject to limitations when
the two motors are operating simultaneously. Like
the previous mechanical structures, the encoders do
not provide direct feedback of the plate’s angular
movements. Inaccurate feedback will deteriorate the
overall performance of the closed-loop system. Such
limitations are not desirable for a setup intended to
test nonlinear topologies. Section 3 discusses the ball
and plate hardware that we designed and constructed
to overcome the limitations imposed by the already
available structures.
The rest of the paper is organised as follows. Section
2 introduces the mathematical properties of the ball
and plate system. This is followed by a detailed expla-
nation of the constructed experimental setup, which
is one of the contributions of this paper. Section 4
focuses on the design of the standard linear topol-
ogy that was implemented on the ball and plate sys-
tem. The following section describes the sliding mode
scheme and how this was adapted to tackle a multi-
variable control problem like the ball and plate sys-
tem. Section 6 evaluates the resulting robust response
that was obtained when the sliding controller was im-
plemented on the experimental setup. The proposed
robust control scheme and its experimental compari-
son and evaluation constitute the other two contribu-
tions of this work.
ApplicationofSlidingModeControltotheBallandPlateProblem
413

2 MATHEMATICAL MODEL
The full nonlinear model of the ball and plate system
was derived by using the Euler-Lagrange method and
K
¨
onig’s theorem . Table 1 lists the parameters used in
the mathematical derivation of the model.
¨x =
m
b
m
b
+
J
b
r
2
b
−gsinθ
x
+ (x
˙
θ
x
+ y
˙
θ
y
)
˙
θ
x
(1)
¨y =
m
b
m
b
+
J
b
r
2
b
−gsinθ
y
+ (y
˙
θ
y
2
+ x
˙
θ
y
˙
θ
y
(2)
T
x
= (J
px
+ J
b
+ m
b
x
2
)
¨
θ
x
+ 2m
b
x ˙x
˙
θ
x
+ m
b
xy
¨
θ
y
+m
b
˙xy
˙
θ
y
+ m
b
x ˙y
˙
θ
y
+ m
b
gx cos(θ
x
) (3)
T
y
= (J
py
+ J
b
+ m
b
y
2
)
¨
θ
y
+ 2m
b
y ˙y
˙
θ
y
+ m
b
yx
¨
θ
x
+m
b
˙xy
˙
θ
x
+ m
b
x ˙y
˙
θ
x
+ m
b
gycos(θ
y
) (4)
Equations (1) and (2) represent the ball dynamics,
while (3) and (4) represent the plate dynamics. These
mathematical expressions show how the state vari-
ables of the ball and plate setup are interrelated to-
gether in a complicated manner making the system
much harder to control. The effects of these nonlin-
ear terms become more dominant for faster ball and
plate movements, larger plate angles displacements
and the displacement of ball from plate’s centre. A
linear model of the system was derived as shown in
(Awtar et al., 2002) and (Ker et al., 2007). Nat-
urally this linear model approximates the nonlinear
model only for a limited range of operation around
an equilibrium point. If the operating conditions vary
widely, such a linear model becomes inadequate to
represent of the actual system behaviour. Section 4
explores how these approximations limit the perfor-
mance that can be reached by standard linear regula-
tors since their design procedures are based on such
linear models. The implementation of more complex
control topologies, like sliding mode control, should
lead to a faster and more accurate performance as well
as a larger range of operation, since they are not based
on linear models.
3 THE EXPERIMENTAL SETUP
From the mathematical analysis presented in Section
2, it can be concluded that the physical ball and
plate setup should ideally allow large angular dis-
placements. Recall that the nonlinear terms are more
dominant when the system is operated with faster
and larger plate angles. The mechanical linkage
Table 1: Parameters of ball and plate mathematical model.
Symbol Units Description
m
b
kg Mass of the ball
r
b
m Radius of the ball
J
b
kgm
2
Moment of inertia of the Ball
x m Ball’s position along the x-axis
y m Ball’s position along the y-axis
θ
x
rad Plate tilt angle in the x-axis
θ
y
rad Plate tilt angle in the y-axis
L
x
m Plate’s length along the x-axis
L
y
m Plate’s length along the y-axis
J
px
kgm
2
Plate’s inertia in the x-axis
J
py
kgm
2
Plate’s inertia in the y-axis
T
x
Nm Torque applied in the x-axis
T
y
Nm Torque applied in the y-axis
structures discussed in Section 1, (Moarref et al.,
2008; Awtar et al., 2002), suffer from a very limited
range of inclination angles.
Ideally both actuators should be directly coupled
to the plate’s axis of rotation. One possible way to
achieve this is through a gimbal structure, where
the plate is mounted on a metal frame. We have
designed and constructed such a setup which is
depicted in Figures 2 and 3. The stationary motor
is responsible to turn the whole gimbal structure.
Hence its rotation is directly coupled to the plate’s
and frame’s axis of rotation, similar to the structure
presented in (Moarref et al., 2008). The second actu-
ator provides the second degree of motion by rotating
the plate within the frame structure. This creates a
non-symmetric setup because the stationary motor
needs to move the entire gimbal structure, which
includes the second motor. To balance the greater
load experienced by the stationary motor a smaller
secondary actuator is chosen and a counter-weight is
added to balance the whole structure, when stationary.
Another challenge of the ball and plate problem is
the sensing method used to accurately track the ball’s
position on the plate. Awtar in (Awtar et al., 2002),
presented a number of different sensors that could be
used to track the ball’s position. In this work the vi-
sual tracking method was chosen since the plate pro-
vides a plain black background that contrasts with the
coloured ball. Hence simpler colour tracking algo-
rithms could be used. Still a personal computer is
not the best machine to handle the computational de-
mands required by real-time image processing algo-
rithms. Hence an intelligent visual sensor was used,
namely the CMUcam4. This visual module does all
the required image processing algorithms on board,
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
414

Camera
Metal Frame
Plate
Motor Hubs
Counterweight
Base
Stationary
Motor
Motor
Encoder
Encoder
Figure 2: The mechanical design of the proposed ball and
plate system.
Figure 3: The constructed ball and plate system.
by dividing the computations between eight proces-
sors working simultaneously. Hence it is able to track
and provide the ball’s location, to the main process-
ing unit, at a 30Hz rate. This tracking update rate
was verified that is high enough to capture the desired
closed-loop dynamics.
4 LINEAR CONTROL
TOPOLOGIES
Classical control is a mature field of study offering a
set of powerful tools for the analysis and design of
linear time-invariant systems. Section 1 showed how
standard classical topologies, like the state-feedback
controller, have successfully been applied to the ball
and plate problem. These methods are based on the
linearised state-space models of the nonlinear ball
and plate dynamics shown in (1) - (4). The pole-
placement design procedure entails the selection of
appropriate state-feedback gains, that enforce the de-
sired closed-loop eigenvalues. The full-state control
feedback law, u, is given by:
u = −K
T
x + gr (5)
where:
r is the desired reference input.
K is a gain matrix that ensures that the system
achieves the desired closed-loop eigenvalues.
x is the state vector of the system.
g is the feedforward gain that ensures zero steady-
state error between the system’s output and its ref-
erence input.
Figure 4 shows how this topology is applied to
the ball and plate problem. Note that the block
diagram does not show the inner-most loop which
controls the armature currents requested by the outer
state-feedback regulators. In this case the current
response is assumed to be instantaneous with respect
to the state-feedback regulator. Another observation,
from Figure 4, is that two state-feedback regulators
are required to control the two axes of the system.
This is due to the linearisation process presented in
Section 2 which decouples the two axes of the ball
and plate system from each other. Hence, when using
classical control design procedures, like the state-
feedback linear regulators, the effects introduced by
cross-coupling terms are ignored. Recall from the
nonlinear model, shown in (1) - (4), that these terms
become more dominant for larger non-equilibrium
conditions and thus limit the type and range of
achievable performance. This is further discussed in
Section 6.
The state-feedback regulator, shown in Figure 4, is
unsuitable for continuously changing inputs or in
cases where the system is subjected to external dis-
turbances. Hence an extra integral action is added to
the feed forward path of each regulator. This modifi-
cation adds another state variable to both axes while
leaving the actual design process, for the calculation
ApplicationofSlidingModeControltotheBallandPlateProblem
415

of value K, unchanged. The results shown in Sec-
tion 6 were obtained with this modified state-feedback
topology, which is usually referred to as the state-
feedback tracker.
Ball &
Plate
Model
T
x
T
y
x=[x ˙x θ
x
˙
θ
x
]
T
y=[y ˙y θ
y
˙
θ
y
]
T
K
x
T
K
y
T
x
y
g
x
g
y
x
ref
y
ref
+
+
Figure 4: Linear regulator topology.
5 SLIDING MODE CONTROL
Sliding mode control aims to enforce the system tra-
jectories into a desired manifold in order to obtain the
desired closed-loop dynamics. This is achieved by
using a discontinuous control action (Slotine and Li,
1991). This topology can guarantee a suitable system
response even in the face of model uncertainties and
external disturbances. Moarref (Moarref et al., 2008)
shows only one set of results from the experimental
implementation of the sliding mode controller, where
the ball had to balance at the centre of the plate. The
plot indicates that the ball took approximately nine
seconds to stabilise at the origin. In (Liu and Liang,
2010) and (Liu et al., 2009) the authors manage to
simulate this nonlinear control topology on the ball
and plate model. Liu and Liang, specify that they
used a double feedback structure to control the full
ball and plate dynamics (Liu and Liang, 2010). On
the other hand (Liu et al., 2009) assumes that the
plate dynamics do not affect the ball’s position. In
both cases, only the ball dynamic equations are used,
and an ideal servo response is assumed for the plate
dynamics. This assumption was made due to the
limitations of standard sliding mode control design
topologies, which are based on nonlinear models
that have a scalar output and are affine in the control
input. Hence the simulations, in both papers ignore
the effects introduced by the plate dynamics.
Figure 5 shows the full sliding mode control topology
that we are proposing and that we have implemented
on the constructed ball and plate experimental testbed,
presented in Section 3. To control the plate dynamics
a PID controller was designed, leading to a total of
three cascaded loops. Figure 5, like Figure 4, does not
show the inner-most current loop since it is assumed
that this exhibits an instantaneous response with re-
spect to the control actions requested by the PID reg-
ulators. Ideally the PID controllers should also ap-
pear instantaneous with respect to the switching con-
trol action that is requested by the outer sliding mode
controllers. The high control activity requested by the
sliding controller is very difficult to achieve with any
mechanical servo mechanism, resulting in a degrada-
tion of the system’s output response. Recall that the
simulation results shown in (Liu and Liang, 2010) and
(Liu et al., 2009) did not take into consideration the
plate dynamics and their effects. But such matters
cannot be ignored when the proposed scheme is to
be implemented and validated on the the constructed
ball and plate hardware. This is further discussed in
Section 6.
Ball &
Plate
Model
T
x
T
y
P ID
x
P ID
y
θ
x
θ
y
θ
x
ref
θ
y
ref
SM C
x
SM C
y
+
+
x
ref
y
ref
+
+
x
y
+
+
Figure 5: The sliding mode control topology.
The works in (Liu and Liang, 2010) and (Liu et al.,
2009) differ in the way they tackle the nonlinearities
present in the ball dynamic equations. Liu and Lang
remove the cross-coupling terms leading to a decou-
pling of the two axes In (Liu et al., 2009) the au-
thors assume a plate deflection of ±5
o
, leading to the
removal of trigonometric terms from the mentioned
equations. Unlike (Liu and Liang, 2010), the authors
of (Liu et al., 2009) retain the cross-coupling terms
which are estimated through an uncertain item ob-
server. More accurate system dynamics would reduce
the need for large switching functions to ensure sys-
tem robustness. For the scope of this research the ef-
fects introduced by the cross-coupling terms were not
considered during the design procedure. Equation (1)
describes the ball dynamics, in the x-direction, of the
ball and plate system. Removing the cross-coupling
terms from (1) results in the standard affine nonlinear
second order model:
¨x =
1
m
b
+
J
b
r
2
b
(−m
b
gsinθ
x
) = bu(θ
x
) (6)
where:
u(θ
x
) = sinθ
x
and b =
−m
b
g
m
b
+
J
b
r
2
b
The primary aim of the discontinuous switching con-
troller is to impose the desired dynamics on the sys-
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
416

tem being controlled. For a second order system, the
resulting surface s would have the following form:
s =
˙
˜x + λ ˜x (7)
where:
˜x = x − x
d
is the tracking error between the sys-
tem’s output and the desired reference input, x
d
.
λ is a strictly positive constant that sets the desired
dynamics of the sliding surface.
The switching action ensures that the state trajectory
of the system reaches and remains on the sliding sur-
face. Once the state trajectorby reaches the sliding
surface, the dynamics defined by λ will be imposed on
the system’s output response. Another action that can
be added in conjunction with the switching function is
the equivalent control term, u
eq
. To obtain the u
eq
ex-
pression, ˙s is assumed to be equal to zero and ¨x terms
are substituted with (6). Theoretically the derived ex-
pression would result in a continuous control law that
can maintain the trajectory on the desired sliding sur-
face provided that the exact model of the system is
known. In this case equivalent control could theo-
retically replace the discontinuous control function.
Practically this is never the case due to model uncer-
tainties and external disturbances present in the actual
system. Hence the following control action is used:
u = arcsin
1
ˆ
b
¨x
d
− λ
˙
˜x − βsgn(s)
(8)
where:
ˆ
b is an estimate of the nonlinear model coefficient
b, shown in (6).
βsgn(s(t)) is the bang-bang action, multiplied by
a gain β, which ensures the system’s robustness.
One of the greatest advantages of this topology is
the intuitive tuning of control parameters λ and β,
due to the sliding mode’s order reduction property.
Control parameter λ has a direct influence on the
control bandwidth of the whole system. Two factors
that limit the selection of λ, hence limiting the
performance that can be achieved by the system, are
neglected time delays and the control loop’s available
sampling rate. Switching gain β determines how
fast the trajectory is moving towards the surface
and the resulting switching that slides the trajectory
along the selected sliding surface. When selecting
parameter β a compromise between a faster response
and smaller chattering effects must be found. Proper
selection of these control variables should lead to an
asymptotically stable system as discussed in (Liu and
Liang, 2010).
Each paper contributed different terms to the standard
sliding mode control equation, shown in (8), to im-
prove the overall performance of the system. In (Liu
and Liang, 2010), the authors add the proportional
term αs(t) which reduces the time the trajectory takes
to reach the sliding surface. On the other hand, in
(Moarref et al., 2008) the authors tried to eliminate
the chattering effects by replacing the discontinuous
signum function with a continuous saturating func-
tion. Another modification is to add an integral term
to the sliding surface which will improve the con-
troller’s performance to continuously changing refer-
ence inputs. When adding the integrator to the sliding
mode controller, (8) changes to:
u = arcsin
1
ˆ
b
¨x
d
− 2λ
˙
˜x − λ
2
˜x − βsgn(s)
(9)
6 RESULTS AND EVALUATION
This section will focus on the results obtained when
the presented control topologies where applied to the
constructed hardware. Figure 6 shows the results ob-
tain when the linear full-state tracker and the sliding
mode tracker were implemented on the constructed
ball and plate system. Recall from Section 4 that
linear control topologies do not take into considera-
tion nonlinear and cross-coupling terms. These terms
become more dominant with faster responses and
larger ranges of operation. Faster specifications al-
ways result in smaller ranges of operation and stabil-
ity. Hence the performance requirements had to be
limited to ensure that the ball reached the desired tra-
jectory even if its initial conditions are not on the de-
sired trajectory. For successful operation the tracker
specifications had to be decreased to a 0.6s rise time
and a 15% peak overshoot. Faster requirements are
possible, but would not guarantee stability if the ini-
tial position of the ball is not on the desired trajectory.
For the set specifications the following tracker param-
eters were derived:
K
x
T
=
−18.43 −7.023 10.41 1.049
K
y
T
=
−5.412 −1.783 2.643 0.2689
g
x
= −23.86 g
y
= −6.059
The linear tracker results, in Figure 6, show how
the system behaves when subjected to a sinusoidal
reference input with a ±0.12m magnitude and
frequency of 0.1Hz. The tracker’s response resulted
in an attenuated output that lagged behind the desired
reference input. The resulting root mean square
(RMS) tracking errors, for the x and y axes, were
equal to 0.0545m and 0.0497m respectively. The
ApplicationofSlidingModeControltotheBallandPlateProblem
417

0 10 20 30
-0.1
-0.05
0
0.05
0.1
x-axis position (m)
Time (s)
x-axis position (m) vs Time (s)
0 10 20 30 40
-0.15
-0.1
-0.05
0
0.05
0.1
y-axis position (m)
Time (s)
y-axis position (m) vs Time (s)
0 2 4 6 8 10
-0.1
-0.05
0
0.05
0.1
x-axis position (m)
Time (s)
x-axis position (m) vs Time (s)
0 2 4 6 8 10
-0.1
-0.05
0
0.05
0.1
y-axis position (m)
Time (s)
y-axis position vs Time (s)
Linear Tracker Results
Sliding Mode Tracker Results
Figure 6: Results obtained when Linear and Sliding Mode
trackers were applied to the ball and plate setup.
observed output delay and attenuation continued to
increase when faster reference inputs were requested.
The resulting tracking error, when the reference input
was increased to 0.3Hz, increased to 0.1217m and
0.113m for the x and y axes respectively. These large
delays and errors are due to the system’s closed-loop
bandwidth which is unable to handle such high-speed
dynamics. On the other hand faster closed-loop
bandwidths are not possible due to the limitations
introduced by the unaccounted nonlinear terms.
The sliding mode control topology presented in Sec-
tion 5 does not take into consideration the plate dy-
namics of the ball and plate system. Hence a PID con-
trol loop was added between the outer sliding mode
controller and the inner torque controller to control
the plate dynamics. Recall that the high control ac-
tivity requested by the sliding controller is very diffi-
cult to achieve with any mechanical servo mechanism.
The best performance that was achieved by the PID
controller was insufficient to keep up with the discon-
tinuous switching control action that was being up-
dated every 0.033s. This would result in an imperfect
and delayed sliding control action which would re-
sult in a degradation of the system’s output response
and an increase in the chattering problem. The ef-
fects introduced by the plate dynamics are not shown
in (Liu and Liang, 2010) and (Liu et al., 2009) since
both papers assumed an ideal servo response in their
simulations. Despite these limitations, when apply-
ing the switching control action shown in (9), we still
managed to obtain a very accurate tracking response.
The sliding mode control parameters β and λ were
heuristically tuned according to the selection criteria
discussed at the end of Section 5:
β = 0.35 λ = 2.5
The sliding mode tracker results, in Figure 6, show
the system’s output response when it was subjected to
a sinusoidal signal with a magnitude of ±0.11m and a
frequency equal to 0.3Hz. The resulting RMS track-
ing errors for the x and y axes were equal to 0.0055m
and 0.0096m respectively. Unlike the linear tracker
scenario, the trajectory response of the sliding con-
troller was not limited to ±0.11m but during opera-
tion the magnitude of the sinusoidal reference input
was successfully increased to ±0.14m without deteri-
orating the overall response of the system. Hence the
sliding mode controller managed to get a faster and
more precise response for bigger ranges of operation.
This is due to the controller’s robust nature which
makes the output response more insensitive to the in-
creasing effects introduced by the nonlinear dynamics
present in the system. Moreover, in contrast to the lin-
ear controller, the sliding-mode scheme managed to
cope very well even in cases when the plant dynamics
were modified deliberately, by changing the ball with
one that is forty times heavier (a metal ball bearing
instead of a tennis ball). In the case of the sliding-
mode controller there was no degradation in perfor-
mance, while the linear controller simply went unsta-
ble. This verifies experimentally that proposed con-
troller is very robust to high variations in the model
parameters.
It is interesting to note that the sliding mode controller
does not perform well when subjected to constant ref-
erence inputs, even when the plate dynamics were
not being considered in the simulation environment.
In this case the sliding mode response of the system
was never able to reach the speed and range that was
achieved with the linear state-space regulator. This is
due to the equivalent control action which is working
against the switching function during the initial phase
when the system’s trajectory is reaching the sliding
surface. This scenario is made worse by the imperfect
switching introduced by the slow plate dynamics and
the large β values due to the motors’ dead-zones. The
latter effects were reduced by switching the signum
function with a saturation function, at the expense of
reducing the controller’s robustness.
7 CONCLUSION
In this paper a mechatronic design of the ball and
plate system was presented. Two different control
schemes were presented and their respective perfor-
mance, was experimentally validated on a physical
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
418

testbed that was designed and constructed for the
purpose of this research. Linear state-feedback
controller was discussed in detail. This was fol-
lowed by an analysis of the results obtained by the
sliding mode controller. When compared to the lin-
ear tracker results, the sliding controller managed to
obtain a more precise response at much higher speeds.
The imperfect switching, introduced by the servo-
loop which could not handle the high control activ-
ity requested by the sliding mode controller, was one
of the main factors which limited the performance of
this robust control strategy. Future research should fo-
cus on designing a switching function that takes into
consideration all the states of the system. Hence ef-
fectively designing a multidimensional sliding mode
controller that would consider both the ball and plate
dynamics.
ACKNOWLEDGEMENTS
This research was partially funded by the Strate-
gic Educational Pathways Scholarship (Malt). This
Scholarship is part-financed by the European Union
- European Social Fund (ESF) under Opera-
tional Programme II - Cohesion Policy 2007-
2013,“Empowering People for More Jobs and a Better
Quality of Life”.
REFERENCES
Awtar, S., Bernard, C., Boklund, N., Master, A., Ueda, D.,
and Craig, K. (2002). Mechatronic design of a ball-
on-plate balancing system. Mechatronics, 12(2):217–
228.
Ho, M.-T., Rizal, Y., and Chu, L.-M. (2013). Visual ser-
voing tracking control of a ball and plate system: De-
sign, implementation and experimental validation. In-
ternational Journal of Advanced Robotic Systems, 10.
Hongrui, W., Yantao, T., Siyan, F., and Zhen, S. (2008).
Nonlinear control for output regulation of ball and
plate system. In Control Conference, 2008. CCC
2008. 27th Chinese, pages 382–387. IEEE.
Jadlovska, A., Jajcisi, S., and Lonscak, R. (2009). Mod-
elling and pid control design of nonlinear educational
model ball and plate. In Proceedings of the 17th
International Conference on Process Control 2009,
pages 475–483. Slovak University of Technology in
Bratislava.
Ker, C. C., Lin, C. E., and Wang, R. T. (2007). Tracking
and balance control of ball and plate system. Journal
of the Chinese Institute of Engineers, 30(3):459–470.
Khalil, H. K. (2002). Nonlinear systems, volume 3. Prentice
Hall Upper Saddle River.
Liu, D., Tian, Y., and Duan, H. (2009). Ball and plate con-
trol system based on sliding mode control with uncer-
tain items observe compensation. In Intelligent Com-
puting and Intelligent Systems, 2009. ICIS 2009. IEEE
International Conference on, volume 2, pages 216–
221. IEEE.
Liu, H. and Liang, Y. (2010). Trajectory tracking sliding
mode control of ball and plate system. In Informatics
in Control, Automation and Robotics (CAR), 2010 2nd
International Asia Conference on, volume 3, pages
142–145. IEEE.
Moarref, M., Saadat, M., and Vossoughi, G. (2008). Mecha-
tronic design and position control of a novel ball
and plate system. In Control and Automation, 2008
16th Mediterranean Conference on, pages 1071–
1076. IEEE.
Slotine, J.-J. E. and Li (1991). Applied nonlinear control,
volume 199. Prentice hall New Jersey.
Wang, H., Tian, Y., Sui, Z., Zhang, X., and Ding, C. (2007).
Tracking control of ball and plate system with a dou-
ble feedback loop structure. In Mechatronics and
Automation, 2007. ICMA 2007. International Confer-
ence on, pages 1114–1119. IEEE.
Wang, Y., Li, X., Li, Y., and Zhao, B. (2012). Identifi-
cation of ball and plate system using multiple neural
network models. In System Science and Engineer-
ing (ICSSE), 2012 International Conference on, pages
229–233. IEEE.
Yuan and De-hu (2009). Pneumatic servo ball and plate sys-
tem based on touch screen and oscillating cylinder. In
Intelligent Systems and Applications, 2009. ISA 2009.
International Workshop on, pages 1–4. IEEE.
Yuan, D. and Zhang, Z. (2010). Modelling and con-
trol scheme of the ball–plate trajectory-tracking pneu-
matic system with a touch screen and a rotary cylinder.
IET Control Theory & Applications, 4(4):573–589.
ApplicationofSlidingModeControltotheBallandPlateProblem
419
