
Integrating Particle Swarm Optimization with Analytical Nonlinear
Model Predictive Control for Nonlinear Hybrid Systems
Jean Thomas
FIE, Beni-Suef University, Ben-Suef, Egypt
Keywords: Hybrid Systems, Nonlinear Model Predictive Control, Particle Swarm Optimization.
Abstract: The computation load remains the main challenge facing the control techniques of hybrid systems with
discrete and continuous control signals. In this paper, a new hybrid controller based on Analytical Nonlinear
Model Predictive Control (ANMPC) and Particle Swarm Optimization (PSO) for nonlinear hybrid systems
is presented. The proposed controller offer sub-optimal solution in reasonable time while respecting the
given constraints. The new developed technique is not considered as a computation burden, thus real-time
implementation is possible for many hybrid systems. Besides, it can be applied directly to the nonlinear
models, avoiding linearization which may lead to inaccurate model and unexpected behaviour. An
application of the proposed controller to a three tanks example is presented.
1 INTRODUCTION
Many real systems can be modelled as hybrid
systems with discrete and continuous input signals.
Several control techniques have been proposed in
literature to control hybrid systems, among them
Model Predictive Control (MPC) has been
considered as one of the most effective techniques
that can control linear hybrid systems. However the
computation burden associated with the mixed
integer linear/quadratic optimization problems
remains the main challenge facing real-time
application. Several techniques and algorithms have
been proposed in literature to reduce the
computation load; for example (Thomas et al., 2003,
2004) proposed using multi-MLD models rather
than using one global Mixed Logical Dynamical
(MLD) (Bemporad and Morari, 1999) model with
bigger number of variables, in (Thomas et al., 2006)
a MPC for state partition based MLD model is
proposed to use simpler models. A techniques based
on genetic algorithm is proposed in (Olaru et al,
2004) and in (Thomas et al., 2005). Explicit-MPC is
proposed in (Bemporad et al., 2000a and 2000b)
where the optimization problem is treated as a multi-
parametric problem solved off-line; and hence on-
line computation reduces to a function evaluation.
However, all these techniques have been developed
for linear hybrid systems.
An Analytical Nonlinear Model Predictive
Control (ANMPC) technique for linear induction
motor is proposed in (Thomas and Hansson, 2010
and 2013), and ANMPC for nonlinear hybrid
systems with discrete inputs only is presented in
(Thomas, 2012). The proposed ANMPC controller
based on enumerating all possible inputs
combination and calculating analytically the cost
function and then selects the input combination
which minimizes the cost function. The author of
(Thomas, 2012) shows that ANMPC lead to MPC
with lower computation load compared to other
techniques proposed in literature i.e. standard B&B,
explicit MPC for the considered classes of hybrid
systems with discrete inputs only, and that ANMPC
an take into account state and output constraints.
This paper propose extending the ANMPC
controller by integrating it with Particle Swarm
Optimization (PSO) (Kennedy and Eberhart, 1995)
and show that the new proposed controller can be
applied effectively to nonlinear hybrid systems with
discrete and continuous inputs. This algorithm
reduces efficiently the computation load while
respecting the given input, states and output
constraints. Besides, the new proposed technique
can control directly nonlinear hybrid systems
avoiding linearization which may lead to inaccurate
model and unexpected behaviour.
The rest of the paper is organized as following;
section 2 briefly presents the concepts of MPC and
294
Thomas J..
Integrating Particle Swarm Optimization with Analytical Nonlinear Model Predictive Control for Nonlinear Hybrid Systems.
DOI: 10.5220/0005570702940301
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 294-301
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

PSO. The proposed ANMPC integrated with PSO
controller is developed in section 3. Application of
the proposed controller to a three-tanks example is
considered in section 4. Finally conclusion and some
remarks are given in section 5.
2 CONCEPTS OF MPC AND PSO
CONTROLLERS
2.1 Model Predictive Control
Predictive control was first developed at the end of
1970s, and was published by Richalet et al., (1978).
In the 1980s, many methods based on the same
concepts are developed. Those types of controls are
now grouped under the name Model Predictive
Control (MPC) (Camacho and Bordons, 1999). MPC
has proved to efficiently control a wide range of
applications in various industries.
The main idea of predictive control is to use a
model of the plant to predict future outputs of the
system. Based on this prediction, at each sampling
period, a sequence of future control values is
developed through an on-line optimization process,
which maximizes the tracking performance while
satisfying constraints. Only the first value of this
optimal sequence is applied to the plant. The whole
procedure is repeated again at the next sampling
period according to the ‘receding’ horizon strategy
(Maciejowski, 2002). The objective is to lessen the
future output error to zero with minimum input
effort. The cost function to be minimized is
generally a weighted sum of square predicted errors
and square future control values, e.g., in Generalized
Predictive Control (Clarke et al., 1987):
[]
[]
=
=
−++
++−+=
u
N
j
N
j
u
jku
jkwkjkyNNJ
1
2
1
2
)1(
)()(
ˆ
),(
λ
β
(1)
where
uy,
ˆ
are the predicted output and the control
signal respectively.
u
NN,
are the prediction
horizons and the control horizon, respectively.
λ
β
,
are weighting factors. The control horizon permits a
decrease in the number of the calculated future
control assuming
0)( =+Δ jku
for
u
Nj ≥
.
)( jkw +
is the reference trajectory.
Constraints over the control signal, the outputs
and the control signal changing, can be added to the
cost function:
maxmin
maxmin
maxmin
)(
)(
)(
ykyy
ukuu
ukuu
≤≤
Δ≤Δ≤Δ
≤≤
(2)
The solution of (1) gives the optimal sequence of
the control signal over the horizon
u
N
while
respecting the given constraints of (2).
A fundmental difficulty of the MPC approach is
the requirement to solve constrained nonlinear,
nonconvex optimization problems. A linearized
model of nonlinear systems is commonly used for
MPC controller. However, this lineariza-tion
introduce model mismatches which affect the
control performance, as the MPC performance
depends largely on the accuracy of the process’
model.
2.2 Particle Swarm Optimization
The particle swarm optimization (PSO) algorithm is
a population-based search algorithm inspired by the
social behavior of birds within a flock (Kennedy and
Eberhart, 1995). Particle Swarm has two primary
operators: Position and Velocity. Each particle
representing a potential solution is maintained
within a swarm. The position of each particle is
adjusted according to the experience of itself and its
neighbours. During each generation, each particle is
accelerated toward the particle’s previous best
position
p
, and the global best position
g
. At each
iteration, a new velocity value for each particle is
calculated based on its current velocity, the distance
from its previous best position, and the distance
from the global best position. The new velocity
value is then used to calculate the next position of
the particle in the search space. This process is then
reiterated a set number of times, or until a minimum
error is achieved. The PSO with Constriction
Coefficient is considered where velocity and
position are updated according to the following
equations (Clerc and Kennedy, 2002):
))]1((
))1(()1([)(
22
11
−−+
+−−+−=
txgrc
txprctvtv
ijj
iijijij
χ
(3)
)()1()( tvtxtx
ijijij
+−=
(4)
where
)(tx
ij
,
)(tv
ij
and
ij
p
are the position,
velocity and best personal position of particle
i
, in
dimension
x
nj ,,2,1 =
at iteration
t
, where
x
n
is
the dimension of the system inputs.
j
g
is the global
best position in dimension
j
.
1
c
and
2
c
are
IntegratingParticleSwarmOptimizationwithAnalyticalNonlinearModelPredictiveControlforNonlinearHybrid
Systems
295

constants, and
1
r
,
2
r
are random values in the
range [0;1].
χ
is the constriction coefficient.
PSO has been found to be robust in solving
continuous nonlinear optimization problems as well
as capable of generating high quality solutions with
more stable and faster convergence characteristics,
and shorter calculation times than other stochastic
methods. It has been shown in the literature that
PSO can efficiently control wide range of systems
especially those with continuous control signals, see
for example (Sedighizadeh and Masehian, 2009),
(Poli, 2008) and references therein.
3 INTEGRATING PSO WITH
ANMPC FOR NONLINEAR
HYBRID SYSTEMS
The main ideas of the proposed controller;
integrating Particle Swarm Optimization with the
Analytical Nonlinear Model Predictive Control
(PSO-ANMPC), for nonlinear hybrid systems are:
• Using the PSO algorithm, find iteratively the
optimal/sub-optimal solution for the continuous
control signals that minimize the fitness function.
• For each solution (particle) of the continuous
control signals, find the best combination of the
discrete control signals using the ANMPC.
• The fitness function of the PSO is the
optimization cost function of the MPC controller.
Each particle’s position in the swarm integrated
with its best combination of discrete inputs, together,
represents a solution to the NMPC optimization
problem. i.e., the inclusion of the control sequence
over the control horizon. Thus, each particle
dimension is
uc
Nn ×
, and the dimension of the
optimization vector of the ANMPC is
ud
Nn ×
,
where
dc
nn , are the number of continuous input
variables and discrete input variables respectively.
The effectiveness of each solution is calculated
through the fitness function, which in this case is the
considered cost function of the NMPC controller.
However, it is important to mention here that PSO is
a gradient-free technique, thus any cost function that
represents the desired behavior can be chosen. The
proposed technique avoids any linearization
technique for minimization, albeit at an increased
computational complexity.
The global best PSO is considered where each
particle is connected to and able to obtain
information from every other particle in the swarm.
(Bratton and Kennedy, 2007). Global best PSO
exhibits very fast convergence rates which are much
needed for predictive control application.
Considering the discrete input variables, there
are limited or finite numbers of possible input
combinations for the discrete input variables i.e.
d
u
d
k χu ∈)(
, where
d
u
χ
is the set of possible
discrete input combinations. Thus the optimal
control signal for these variables will be one
combination of the possible input combinations.
The PSO-ANMPC can be implemented through
the following Algorithm:
Algorithm 1
1- Let
k
p
is a particle in the swarm for
d
Nk ,,2,1 =
, where
d
N
is number of
particles in the population.
[
]
)1(,),1(),(: −++== Nkkkp
cccckk
uuuu
and let:
[
]
d
u
ddddi
Nkkk χuuuu ∈−++= )1(,),1(),(
is the i-
th
possible discrete control sequence
over horizon N
2-
Initializing the particles position and velocity
of the PSO, and let
∞=
opt
J
3-
For
t
Nj :1=
(
t
N
max. number of iterations)
4-
For each
k
p
5-
while
d
u
χ
is non empty, where
d
u
χ
is
the set of possible input combinations
over horizon N
6-
Select
d
u
i
χu ∈
, and remove it from
the set
d
u
χ
7-
Compute
i
J the cost function
according to the control combination
ܝ
, where:
[]
T
dci
uuu = .
8-
If
opt
i
JJ <
i
opt
JJ =
, and
i
uu =
*
,
End
end
End
9- update the particles position and velocity
End
10-
i
opt
uu =
*
the optimal control signal
This technique which we call it PSO-ANMPC has
many advantages. It reduces the computation time
significantly; because from one hand: computing
analytically the cost function is faster than building
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
296

or reformulating the problem as MIQP or MILP
problem and then solving it, and from the other hand
the proposed analytical NMPC has often less
number of possible input combination than
formulating it classically in a hybrid system
framework, e.g. MLD systems (Bemborad and
Morari, 1999); to explain that in a simple way,
consider a system with one discrete input variable
which may have a value among
m
possible discrete
values, this will be modeled in the MLD form by
m
binary variables which leads to a number of possible
input combinations over control horizon
N
equal
Nm×
2
, while the number of possible input
combinations with the proposed PSO-ANMPC
controller for the same system will equal
N
m only.
One of the main advantages of the proposed
controller is its ability to deal directly with nonlinear
hybrid systems, where modeling and controlling of
nonlinear hybrid systems is normally a hard task and
it is very common to linearize the model, but this
linearization could lead to a complex system with
many different linear models around different
operating points and/or could introduces uncertainty
which may lead to inaccurate model affecting the
efficiency of designed or used controller. The
advantage of the technique presented here is that we
do not need to linearize the system, and non-linear
dynamics can be directly used to calculate the new
states and outputs. Moreover, The proposed
controller is easy to construct, to tune and to
implement.
3.1 Reduction Algorithm
To avoid examining all possible discrete input
combinations over the control horizon
N
the
flowing Algorithm is proposed.
Algorithm 2
1- Initializing with
0)(, =∞= kJJ
i
opt
2-
For
{}
si
i
,,2,1, ∈u
where ݏ is the total
number of possible input combinations over
horizon ܰ
3-
For
Nj :1=
4-
Compute
)( jkJ
i
+
the cost function
according to the control combination
i
u
for horizon j as follows:
()( )
()
1,
)1()(
−+++
+−+=+
jkjkf
jkJjkJ
i
ii
ux
where
()( )
(
)
1, −++ jkjkf
i
ux
is the cost
at instant
()
jk +
due to the control signal
()
1−+ jk
i
u
.
5-
If
opt
i
JjkJ >+ )(
Break and go to step 2
end
end
6-
At
Nj =
If
)()( NkJJJNkJ
i
optopt
i
+=→<+
end
End
7-
opt
opt
JJ =
*
the optimal solution
Algorithm 2 stops the cost function calculations
at prediction step
()
jk + where
Nj <<1
for the
control sequence
i
u
over the horizon
N
if the cost
function at this prediction step is higher than the
current upper boundary
opt
J
.
Algorithm 2 could also be used as suboptimal
solution if the computation time is higher than the
sampling time, the Algorithm could stop at any
instant and send the control signals according to the
current
opt
J
as a suboptimal solution.
3.2 Constraints
In this section, we describe how system constraints
can be included in the optimization problem so that
PSO-ANMPC can offer a suboptimal solution while
respecting the given constraints.
3.2.1 Input Constraints
Constraints over the control signal
c
j
c
j
c
j
ukuu
maxmin
)( ≤≤
can be implemented by
limiting the search space in the PSO algorithm:
[
]
maxmin
,)(
jjij
xxtx ∈
, where
maxmin
,
jj
xx
are the
control signal constraints
c
j
c
j
uu
maxmin
,
,
respectively, given that the discrete control signals
are limited by their discrete values.
Constraints over the control signal variation
max
)(
jj
uku Δ≤Δ
can be represented through the
particles velocity limits, as follows:
>
≤
=
maxmax
max
)(
)()(
)(
jijj
jijij
ij
VtvifV
Vtviftv
tv
(5)
IntegratingParticleSwarmOptimizationwithAnalyticalNonlinearModelPredictiveControlforNonlinearHybrid
Systems
297

where
maxj
V
is the maximum allowable control
variation for the control element
j
.
3.2.2 Output and System States Constraints
Output signals and system states can be subject to
hard and/or soft constraints. Hard constraints could,
for example, relate to safety or physical constraints,
while soft constraints may be related to economic
constraints or better working conditions.
Both of hard and soft constraints can be included
in the proposed controller. Hard constraints on
output and state variables can be simply considered
by adding the following line to Algorithm 2:
∞=+→> )()()(
maxmax
jkJyxyxif
i
(6)
Thus any control combination which will lead to
violation of the output or state hard constraints will
be avoided.
Soft constraints which allow, at a prise,
temporary the violation of some constraints, can also
be included as following:
ε
+≤ )()(
maxmax
xyxy (7)
Adding the following term to the cost function:
()()
jkQjkjkJ
T
i
+++=+ εε)(
(8)
where
Q
are positive definite weighting matrix.
This additional term in Equation (8) penalize the
violation of soft constraints, pushing the system to
have zeros=
ε . Effectively, we are saying that the
constraints are allowed to be violated to a degree,
but doing so costs, and should thus be avoided if
possible.
4 APPLICATION
The proposed control strategy is applied on the three
tanks example. The simplified physical description
of the three tanks system is presented in Figure 1
(see Dolanc et al., 1997, for more details).
The system consists of three tanks, filled with
water by two independent pumps acting on tanks 1
and 2. These two pumps are continuously
manipulated from 0 up to a maximum flow
1
Q
and
2
Q respectively. Four switching valves
1
V ,
2
V ,
13
V
and
23
V control the flow between the tanks, those
valves are assumed to be either completely opened
or closed (
lyrespective 0or 1=
i
V
). The
3N
V
manual valve controls the nominal outflow of the
middle tank. It will be assumed in further
simulations that the
1L
V
and
2L
V
valves are always
closed and
3N
V
is open. The liquid levels to be
controlled are denoted
1
h
,
2
h
and
3
h
for each tank
respectively.
Figure 1: COSY three tank benchmark system.
The conservation of mass in the tanks provides
the following differential equations:
)
2323
2231313113
(
1
3
)
23232232
(
1
2
)
13131131
(
1
1
N
Q
V
Q
V
Q
V
Q
V
Q
A
h
V
Q
V
QQ
A
h
V
Q
V
QQ
A
h
−+
+++=
−−=
−−=
(9)
where the
sQ'
denote the flows and A is the
cross-sectional area of each of the tanks. The
Toricelli’s law provides the expressions of the flows
through the valves, which are given by the relations:
max
2
33
max
2
2,1,
max
2
33
:where
3333
)
3
,max(),(max(
3
)
3
(
3
3
33
h
g
N
S
z
a
N
k
v
hh
g
i
S
z
a
i
k
i
h
g
i
S
z
a
i
k
h
N
V
N
k
N
Q
h
v
h
i
h
v
h
i
V
i
k
Vii
Q
h
i
h
i
V
i
k
Vii
Q
=
−
=
==
≈
−≈
−≈
(10)
From these expressions, a model is derived with
the following variables:
']
23132121
[
']
321
[
V V V V QQ
h hh
=
=
u
x
(11)
The following specifications are considered:
starting from zero levels (the three tanks being
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
298
empty), the objective of the control strategy is to
reach the liquid levels
m 5.0
1
=h
,
m 5.0
2
=h
and
m 1.0
3
=h
.
As presented in (Thomas et al., 2006), studying
the dynamic behavior of the three tanks, starting
from zero levels to the desired ones, enables to
divide the state space into three main regions, each
one with its adequate simple MLD model; for
example in the sub-region where the liquid level in
the three tanks are less than the valves level, it
clearly appears that the two valves
1
V
and
2
V
of the
input vector are not in progress, thus
']
231321
[ V V QQ=u
.
Obviously the particles of PSO will consider the
continuous signals (the two pumps), while ANMPC
will investigate the best position combination of the
four valves. The proposed PSO-ANMPC has been
implemented in simulation to reach the level
specification with the following parameters: The
parameters of the PSOMPC controller that give a
good response are:
05.2
21
== cc
,
73.0=
χ
, with
10 particles per swarm and a maximum number of
iterations 10. A control horizon
2==
u
NN
is
chosen. Weights in the objective function (1) have
been chosen as
)100000,1000,10000.(diag=
β
and
1=
λ
. Search space and velocity limits are chose
according to the pumps limits as follows:
[]
0001.0,
,,,
0
0
max
max
max
max
max
max
min
max
max
=
−
−
∈
=
=
Qwhere
Q
Q
v
Q
Q
v
Q
Q
x
i
ii
The global best PSO is used for the PSO with a
constriction coefficient. The solution at instant
1−k
is memorized and introduced as a particle in the
initial population at instant
k
. The results are
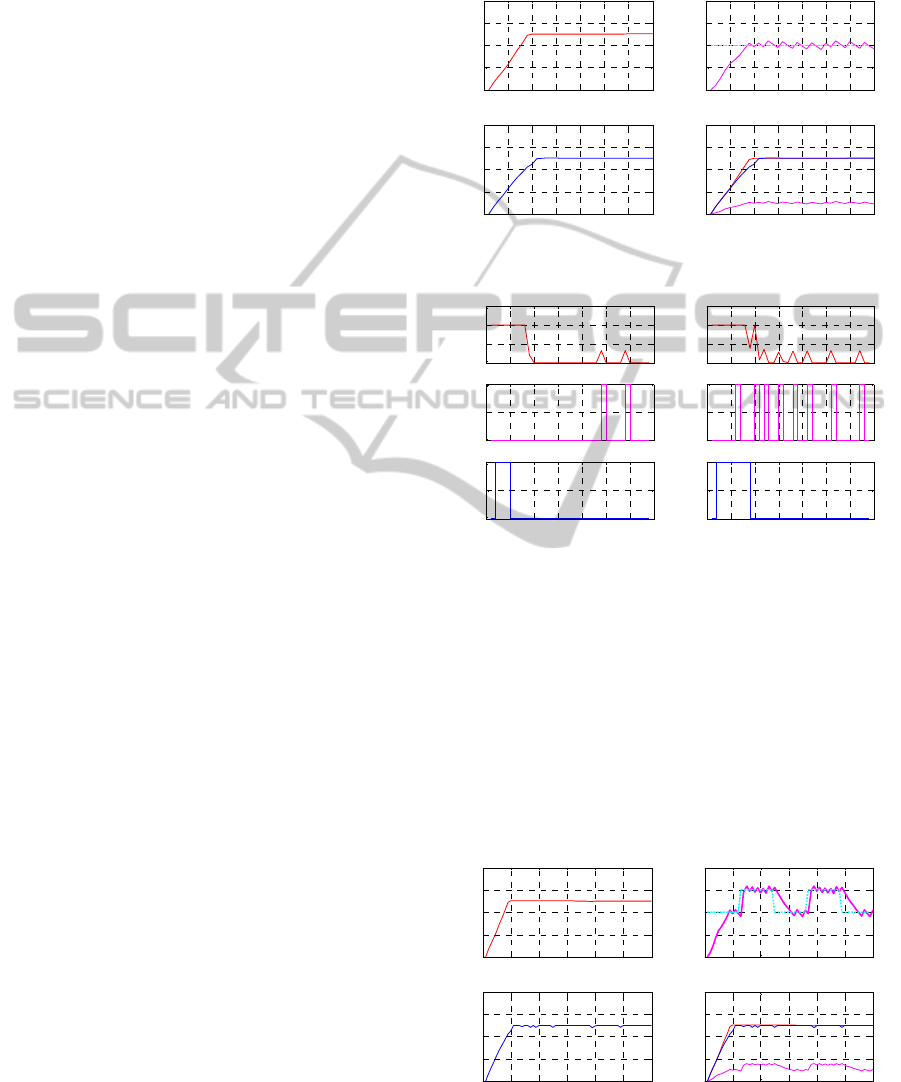
presented on Figure 2 for the tanks levels and on
Figure 3 for the control signals. The level of the
third tank oscillates around 0.1 as
1.0
3
=h
does not
correspond to an equilibrium point. Consequently,
the system opens and closes the two valves
1
V and
2
V
to maintain the level in the third tank around the
desired level of 0.1m. The system has been
simulated in Matlab envirement.
The computation times per step is in order of ms.
i.e. is much smaller than the sampling time (the
sampling time of the three tanks benchmark is 10 s.).
Thus real-time application is possible even for
longer horizon. The PSO-ANMPC technique
reduces the computation time and provides
opportunities for real-time implementation; avoiding
exponential explosion of the algorithm.
Figure 2: Water levels in the three tanks.
Figure 3: Controlled variables.
Figures 4 and 5 respectively present the three
tanks levels and the control signals with PSO-
ANMPC technique, where the desired level in the
third tank is changing. It can be seen that the
proposed controller can successfully tracking the
desired levels. It must be noticed that the variation
of the third tank level from 0.15 to 0.1 takes more
time than the variation from 0.1 to 0.15, due to the
benchmark physical features.
Increasing the number of particles per swarm
and the maximum number of iteration will improve
Figure 4: Water levels in the three tanks –
3
h
changes.
0 5 10 15 20 25 30 35
0
0.2
0.4
0.6
0.8
Level h1
0 5 10 15 20 25 30 35
0
0.2
0.4
0.6
0.8
Sampling Instants
Levels h1, h2 and h3
0 5 10 15 20 25 30 35
0
0.05
0.1
0.15
0.2
Level h3
0 5 10 15 20 25 30 35
0
0.2
0.4
0.6
0.8
Sampling Instants
Level 2
0 5 10 15 20 25 30 35
0
0.5
1
1.5
x 10
-4
Input Q1
0 5 10 15 20 25 30 35
0
0.5
1
1.5
x 10
-4
Input Q2
0 5 10 15 20 25 30 35
0
0.5
1
V1
0 5 10 15 20 25 30 35
0
0.5
1
V2
0 5 10 15 20 25 30 35
0
0.5
1
Sampling Instants
V13
0 5 10 15 20 25 30 35
0
0.5
1
Sampling Instants
V23
0 10 20 30 40 50 60
0
0.2
0.4
0.6
0.8
Level h1
0 10 20 30 40 50 60
0
0.2
0.4
0.6
0.8
Sampling Instants
Levels h1 , h2 and h3
0 10 20 30 40 50 60
0
0.05
0.1
0.15
0.2
Level h3
0 10 20 30 40 50 60
0
0.2
0.4
0.6
0.8
Sampling Instants
Level h2
IntegratingParticleSwarmOptimizationwithAnalyticalNonlinearModelPredictiveControlforNonlinearHybrid
Systems
299
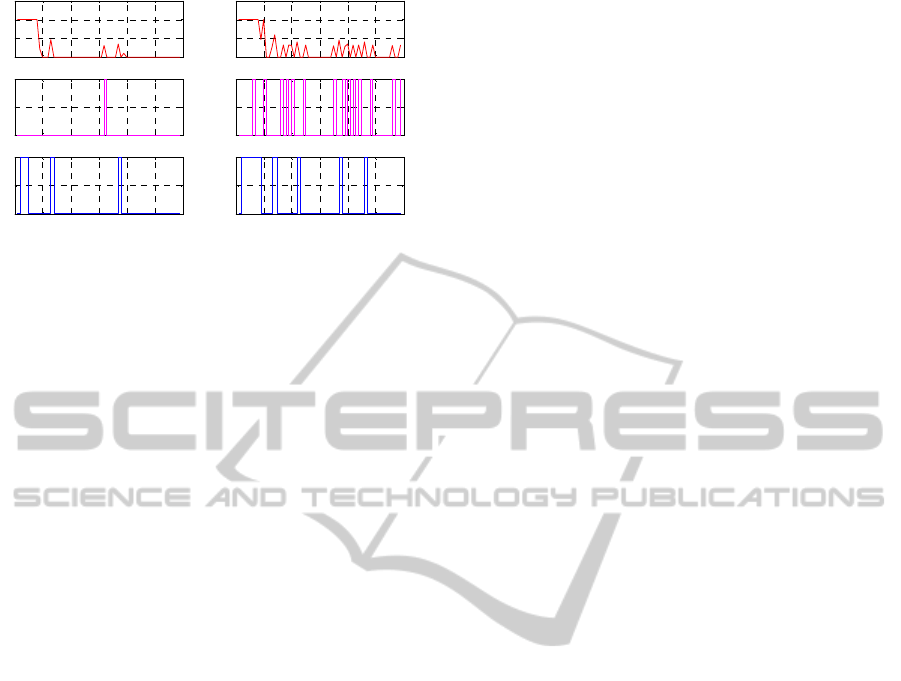
Figure 5: Controlled variables –
3
h
changes.
the suboptimal solution, and increases the
opportunities to find the optimal solution; however
this will increase the computation time. The
selection of the number of particles and the
maximum number of iteration is a trade-off, and is
based on the dynamics of the process to be
controlled.
5 CONCLUSIONS
This paper presented integrating Particle Swarm
Optimization with Analytical Nonlinear Model
Predictive Control (PSO-ANMPC) for constrained
nonlinear hybrid systems with discrete and
continuous control signals. The proposed PSO-
ANMPC controller offers a suboptimal solution in
reasonable time, thus increases the opportunities of
real-time application for many nonlinear hybrid
systems. It can be applied directly to nonlinear
hybrid systems, thus no need to linearize the
nonlinear dynamics as usually done with other
techniques. PSO-ANMPC can be applied to some
classes of hybrid systems including constrained
nonlinear systems, constrained non-convex
optimization problems and fast dynamic hybrid
systems. The proposed controller has the ability to
consider hard and soft constraints. However, there is
no guarantee to find the optimal solution.
An application of the PSO-ANMPC controller to
a three-tanks example showed that it reduces
significantly the computational time, which is an
inherent drawback of classical MPC controllers.
Therefore, real-time implementation of the proposed
PSO-ANMPC controller is possible.
Future work will include experimental works to
validate this technique in practice, as well as,
improving the algorithm and applying it to other
classes of hybrid systems.
REFERENCES
Bemporad A. and M. Morari, 1999. Control of systems
integrating logical, dynamics, and constraints.
Automatica, 35(3):407-427, March.
Bemporad A., F. Borrelli, and M. Morari, 2000a. Optimal
controllers for hybrid systems: Stability and piecewise
linear explicit form. In Proc. 39th IEEE Conf. on
Decision and Control, Sydney, Australia, December
2000.
Bemporad A., F. Borrelli, and M. Morari, 200b. Piecewise
linear optimal controllers for hybrid systems. In Proc.
American Contr. Conf., pages 1190-1194, Chicago,
IL, June 2000.
Bratton D., and J. Kennedy, 2007. Defining a Standard for
Particle Swarm Optimization. Proceedings of the 2007
IEEE Swarm Intelligence Symposium.
Camacho, E. F. et C. Bordons, 1999. Model predictive
control. Springer-Verlag, London.
Clarke, D.W., C. Mohtadi et P. S. Tuffs, 1987.
Generalized predictive control – Part I. and II.
Automatica, Vol.23 (2), pp. 137-160.
Clerc M., and J. Kennedy, 2002. The particle swarm -
explosion, stability, and convergence in a
multidimensional complex space. IEEE Transactions
on Evolutionary Computation, Vol. 6(1): pp. 58-73.
Kennedy, J., Eberhart, R., 1995. Particle Swarm
Optimization. Proceedings of IEEE International
Conference on Neural Network, IV: 1942-1948.
Maciejowski J.M., 2002. Predictive Control. Prentice
Hall.
Olaru Sorin, Jean Thomas, Didier Dumur and Jean
Buisson, 2004. “Genetic Algorithm based Model
Predictive Control for Hybrid Systems under a
Modified MLD Form”, International journal of
Hybrid Systems, Vol. 4 : 1-2, mars-juin 2004.
Poli R., 2008. Analysis of the Publications on the
Applications of Particle Swarm Optimisation. Journal
of Artificial Evolution and Applications, Volume
2008, Article ID 685175, 10 pages.
Richalet J., A. Rault, J. L. Testud et J. Japon. 1978. Model
predictive heuristic control: application to industrial
processes”, Automatica, 14(5), pp. 413-428.
Sedighizadeh D and E. Masehian, 2009. Particle Swarm
Optimization Methods, Taxonomy and Applications.
International Journal of Computer Theory and
Engineering, Vol. 1, No. 5, December 2009. 1793-
8201.
Thomas J., and A. Hansson, 2010. Speed Tracking of
Linear Induction Motor: An Analytical Nonlinear
Model Predictive Controller. In proceeding of
Conference of Control Application CCA’10, Tokyo,
Japan, Sep.
Thomas J., and A. Hansson. Speed Tracking of a Linear
Induction Motor: Enumerative Nonlinear Model
Predictive Control. IEEE Transactions on Control
Systems Technology, Vol.21 (5), pp. 1956-1962, Sept.
2013.
Thomas J., J. BUISSON, D. DUMUR, H. GUÉGUEN,
2003. “Predictive Control of Hybrid Systems under a
0 10 20 30 40 50 60
0
0.5
1
1.5
x 10
-4
Input Q1
0 10 20 30 40 50 60
0
0.5
1
1.5
x 10
-4
Input Q2
0 10 20 30 40 50 60
0
0.5
1
V1
0 10 20 30 40 50 60
0
0.5
1
V2
0 10 20 30 40 50 60
0
0.5
1
Sampling Instants
V13
0 10 20 30 40 50 60
0
0.5
1
Sampling Instants
V23
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
300

Multi-MLD Formalism”, IFAC Conference on
Analysis and Design of Hybrid Systems ADHS 03, pp.
64-69, Saint-Malo, France, Jun. 2003.
Thomas Jean, Didier. DUMUR and Jean BUISSON, 2004.
“Predictive Control of Hybrid Systems under a Multi-
MLD Formalism with State Space Polyhedral
Partition”, American Control Conference ACC’2004,
Boston.
Thomas J., Sorin Olaru, Jean Buisson and Didier Dumur,
2005. “Genetic Algorithm – Quadratic Programming
based Predictive Control for MLD systems”, 15th
International Conference on Control Systems and
Computer Science CSCS15, 25-27 Mai 2005.
Thomas J., D. Dumur, J. Buisson, H. Guéguen, 2006.
"Model predictive control for hybrid systems under a
state partition based MLD approach (SPMLD)",
Informatics in Control, Automation and Robotics I J.
Braz, H. Araujo, A. Vieira et B. Encarnaçao Editeurs,
Springer, pp. 217-224, mai 2006.
Thomas Jean, 2012. Analytical non-linear model
predictive control for hybrid systems with discrete
inputs only. Control Theory & Applications, IET, vol.
6(8), pp. 1080 – 1088, May 2012.
IntegratingParticleSwarmOptimizationwithAnalyticalNonlinearModelPredictiveControlforNonlinearHybrid
Systems
301
