
Periodic Takagi-Sugeno Observers for Individual Cylinder Spark
Imbalance in Idle Speed Control Context
Thomas Laurain
1
, Jimmy Lauber
1
and Reinaldo Palhares
2
1
Laboratory of Automatic Control and Human-Machine Systems (LAMIH), UMR CNRS 8201,
University of Valenciennes, Valenciennes, France
2
Department of Electronics Engineering, Federal University of Minas Gerais, Belo Horizonte, Brazil
Keywords: Discrete Periodic Takagi-Sugeno Observer, Individual Cylinder Observation, Spark Advance, Unbalanced
Cylinders, Idle Speed Control.
Abstract: This paper aims to present a systematic methodology for designing periodic observers for cyclic nonlinear
systems represented by Takagi-Sugeno models. An application to idle speed control of a spark-ignition
engine will be proposed. Thanks to the estimated individual cylinder values, we can detect an imbalance of
each cylinder (unbalanced cylinder). Based on a dynamic hybrid model, some simulation results will prove
the efficiency of our method.
1 INTRODUCTION
In natural as in artificial systems, cyclic behaviors
can be observed (walk action, flying wings, spark-
ignition (SI) engine). The precursor study of
(Bolzern et al., 1986) presents a periodic
representation of such a system and the work of
(Bittanti and Colaneri, 2000) defines the concept of
periodic transfer function.
Regarding the engine application, (Chauvin et
al., 2007) consider the system as continuous-time
linear periodic and build an input estimation for
torque combustion of an engine, which is a critical
value in control problem. Moreover, the system can
be written using a particular discrete-time domain,
the crank-angle domain whose efficiency for this
kind of study has been demonstrated in (Yurkovich
and Simpson, 1997). This work also introduces what
they call “fuzzy control” for automotive
applications, which is close to the Takagi-Sugeno
(TS) (Takagi and Sugeno, 1985) representation used
in the present paper. Discrete-time nonlinear
periodic systems represented by TS models have
been analyzed by plenty of papers, such as (Lendek
et al., 2012) and (Lendek et al., 2013a) for new
Lyapunov functions construction or (Kerkeni et al.,
2009) and (Lendek et al., 2013b) for stabilization.
An application to an automotive problem is
presented in (Kerkeni et al., 2010) to estimate the air
flow inside each cylinder.
The context for this study is idle speed control
(ISC). The regulated value is the engine speed,
which has to be as low as possible to reduce fuel
consumption and pollution during idle phases, but
not too low to avoid stalling. Moreover, disturbances
may occur in this idle phase because of the starter
asking for torque when an electronic device is turned
on (lights, radio, GPS, air conditioner and so on…).
Because it deals with fuel and pollution, this control
problem becomes an environmental one.
The control inputs used for such a control are the
throttle angle that pilots the air entering into the
engine and the spark advance angle. This angle
represents the difference between the moment the
spark appears and the Top Dead Center (TDC).
Concerning our application, it is well known
from (Grizzle et al., 1991) that all the cylinders of an
engine are not working exactly the same way. This
leads to a need of individual spark advance control.
Using spark advance for idle speed control has
been done in many studies from the literature, with
different ways: A mathematical approach taking into
account delay and uncertainties (Bengea et al.,
2004), an electricity one with current ion that
circulates in the spark plug circuit (Shamekhi and
Ghaffari, 2005), a torque-based model and control
with values for simulation (Bohn et al., 2006), a
mathematical set analysis for the problem of safety
in digital control of a linear model (De Santis et al.,
2006), an electronic-based work with knock sensors
302
Laurain T., Lauber J. and Palhares R..
Periodic Takagi-Sugeno Observers for Individual Cylinder Spark Imbalance in Idle Speed Control Context.
DOI: 10.5220/0005570803020309
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 302-309
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

to tune spark advance (Di et al., 2010) or three
control papers that use Adaptive Posicast Control
(APC) and Model Predictive Control (MPC) on
nonlinear models that are linearized by the authors
(Yildiz et al., 2007), (Di Cairano et al., 2008) and
(Di Cairano et al., 2011).
The originality of this paper is to distinguish the
behavior of the different cylinders using individual
cylinder observers in the engine considered as a
discrete-time (crank-angle domain) nonlinear
periodic system. Comparing to the presented studies,
this paper takes into account the nonlinearities
instead of linearizing them.
The paper is organized as follows: first, the
engine model used to develop the observers is
presented, then the observer design methodology is
described and finally some simulations results, based
on different scenarios, are provided.
2 ENGINE MODEL
2.1 Temporal Domain Model
The model used for developing the observers and the
controllers in this paper is mainly based on the work
of (Balluchi et al., 2010) that proposes an hybrid
model (i.e., a continuous-time model triggered with
discrete-time events). The physical phenomena
occurring in the SI engine are modelled with
polynomial equations whose coefficient values are
given for a Magneti Marelli engine. The model is
structured as in Figure 1.
Figure 1: Structure of the engine model.
As detailed in the introduction, the two
controlled inputs of the engine are the throttle angle
in degrees (°) and the spark advance per each
cylinder in degrees before TDC (°). The hybrid
model from (Balluchi et al., 2010) can be translated
into a continuous-time state-space representation:
() () () ()
()
,,
p
load
xt f xt ut T t=
(1)
with 10 states and 2 control inputs:
1
xn=
(speed of the crankshaft in rpm),
2 air
xT=
(torque
produced by the air path in Nm),
3
xp=
(pressure in
the intake manifold in mbar),
4
x
α
=
(throttle angle
in degrees),
5
x
η
=
(efficiency due to spark
advance),
6
x
ϕ
=
(spark advance angle before top-
dead center, in degrees),
7
ii
air
xm=
(mass air flow in
the i-th cylinder) for
{}
1, , 4i ∈…
,
1 thr
ucmd=
(command of the throttle angle in degrees) and
2 spk
ucmd=
(command of the spark advance angle,
same for all spark plug).
Where
()
,,
p
load
fxuT
is a nonlinear function
which depends on continuous event "
()
,,
load
xuT
"
and discrete one "
p
" which corresponds to different
functioning phases of the engine, see table I.
Table 1: Engine phases (in function of crankshaft
degrees).
Phase / Cylinders C1 C2 C3 C4
P1 (0° to 180°) I C H E
P2 (180° to 360°) C E I H
P3 (360° to 540°) E H C I
P4 (540° to 720°) H I E C
Where “I” stands for “Intake”, “C” for
“Compression”, “E” for “Expansion” and “H” for
“Exhaust”. Such a dynamic temporal system can be
written in another base, the crank-angle domain as it
has been presented in the past (Yurkovich and
Simpson, 1997). Moreover, this domain, based on
crankshaft angle, is very close to reality, where the
Eelectronic Controller Unit (ECU) of an engine is
triggered with a sample time related to crankshaft
degrees (for our application, this time is considered
as a signal every six crankshaft degrees to fit our
engine test bench). This signal (i.e., every six
degrees) is doubled with another one when a dead
centre is reached, i.e. every 180 crankshaft degrees.
2.2 Crank-angle Domain Model
The crank-angle domain can be considered as a
special discrete-time domain that can take into
account the “discrete events” described in the hybrid
model from (Balluchi et al., 2010). These events
allow the model simulating the multiple phases of an
engine. As presented in the introduction, such a
change can be represented via a periodic discrete-
time nonlinear system. For a 4-strokes engine, the
phase cycle is completed in 2 rounds, i.e. 720
crankshaft degrees (change of phase every 180
PeriodicTakagi-SugenoObserversforIndividualCylinderSparkImbalanceinIdleSpeedControlContext
303

crankshaft degrees). The conversion starts with
moving from time to crank-angle domain:
dy dy d dy
dt d dt d
θ
ω
θθ
==
(2)
with
ω
speed in degrees per second;
60 1
6
360 6
dy dy n dy dy dy
n
dt d d d n dt
θθθ
== =
(3)
In order to convert nonlinear continuous model
into a discrete one, the Euler transformation is used:
(1) ()
s
dy yk yk
dt T
+−
≈ (4)
Using (4), the following recursive law can be
defined:
()
(1) ()
6
S
T
dy
yk yk
nk d
θ
+= + (5)
where
(1)yk+ denotes the signal taken at the (k+1)
instant and
S
T the sampling time, chosen
appropriately not to lose information.
3 OBSERVER DESIGN
Acting as “virtual sensors”, observers are a good
alternative for automotive problems where adding a
sensor is neither an economic valuable solution nor a
production commodity one. These observers are able
to provide unmeasured information to the controller
in order to ensure the optimization of the engine
functioning.
3.1 Periodic Takagi-Sugeno Observers
In this section, the theory of these particular
observers (i.e., periodic nonlinear ones) will be
presented. Let us consider a reduction of the
previously-detailed model (1) translated into crank-
angle domain with the transformation presented in
(5). For commodity of writing and reading, the term
k will be omitted and the term 1k + will be
represented using a “
+ ” in index:
() ()
p
p
rd rdrd
dr
x
Axx Bxu E
yCx
+
=++
=
(6)
With
p denoting the period, i.e.
{
}
1, , 4p ∈
,
() ()()
6
pp
dSr
A
xITnAx=+
where
()
p
r
A
x
stands for
the matrix of the reduced periodic temporal model
and
()
p
d
A
x
stands for the discrete one, by the same
way,
()
6
S
dr
T
Bx B
n
=
,
dr
CC= and
6
p
p
S
dr
T
EE
n
=
.
Contrary to what can be read into the literature, this
paper presents an alternative of the classical
linearization: Dealing directly with the nonlinearities
of the system using a particular representation of
these nonlinear systems, the so-called Takagi-
Sugeno (TS) models (Takagi and Sugeno, 1985).
These TS models have the advantage of being an
exact representation of the nonlinear model they
represent. Let us consider a model with
m
nonlinearities and their bounds,
max
m
and
min
m
. A TS
model can be written with
2
m
subsystems.
The membership functions must be constructed
with measurable values in order to verify a premise
vector fully measured (i.e.,
() ()
ˆ
zk zk=
). The scalar
nonlinear functions
()
i
hz
must verify the property
of convex sum
()
1
1
m
i
i
hz
=
=
. As presented in plenty
of papers on Takagi-Sugeno models such as (Takagi
and Sugeno, 1985) (Tanaka and Wang, 2001)
(Lendek et al., 2010), the scalar functions are related
to the nonlinearities bounds: The
()
i
hz
can be
obtained using, for instance,
()
max max
max min max min
11
1
11
...
mm
mm
nl nl nl nl
hz
nl nl nl nl
−−
=××
−−
(7)
So, a periodic discrete TS model is obtained from
(6):
()
()
___
1
m
pp
ridirdidi
i
xhzAxBuE
+
=
=++
(8)
From (8), a periodic Takagi-Sugeno (i.e., nonlinear)
observer can be written based on (Guerra et al.,
2012):
()
()
() () ( )
___
1
1
11
ˆˆ
ˆ
m
pp
ridirdidi
i
mm
pp
ii i i
ii
xhzAxBuE
hzS hzK y y
+
=
−
==
=++
+−
(9)
For commodity, the sum of
()
i
hz
is omitted in the
following sections of this paper, and the term
()
_
1
m
p
idi
i
hzA
=
is replaced by
_
p
dz
A
. The product
() ()
1
11
mm
pp
ii i i
ii
hzS hzK
−
==
is written as
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
304

()( )
1
pp
z
z
SK
−
keeping in mind that the z does not
represent the same
()
i
hz
.
In order to study the convergence of such an
observer, the estimation error
ˆ
rrr
x
xx=−
and its
dynamic has to be considered:
()( )
(
)
1
_
ppp
rdzz zdr
x
ASKCx
−
+
=−
……(10)
Let us define the quantities:
1
_
(*)
T
p
p
ij
pp p p p p
jdi jd j j
P
SA KC S S P
+
−
Γ=
−−−+
(11)
Theorem 1: According to what has been
demonstrated in the work of (Kerkeni et al., 2009),
the prediction error is globally asymptotically 4-
periodically stable if there exists symmetric matrices
0
p
P >
, matrices
p
i
S ,
p
i
K
such that the following
LMI conditions from Tuan (Tuan et al., 2001) hold
for all engine phases and
p
ij
Γ
defined in (11):
0
p
ii
Γ< ,
{
}
,1,,4ip∈
(12)
2
0
3
ppp
ii ij ji
Γ+Γ+Γ <
,
{
}
,, 1, ,4,ijp i j∈≠
(13)
3.2 Application to Torque Observers
Three cascade periodic TS observers can be
designed to rebuild the torque produced by spark
advance (see Figure 2).
Figure 2: Cascaded observers.
The first observer will provide the air mass
inside each cylinder using the measures of pressure,
speed, throttle angle and command, thanks to the
following reduced model:
()
1234
3477 77
T
T
r
x
xxxxxx=
(14)
()
131 124
34
1
131
32 34
()()
01
0
VV
thr
r
RT c c x RT s s x
Ax
ccx
τ
×
××
−+ +
−Ο
=
+
ΟΟ
,
41
0
1
rthr
B
τ
×
=
Ο
,
2
42
T
r
I
C
×
=
Ο
()
()
0021
1
1
021
31
0
V
r
RT s c c x
Ex
ccx
×
−−
=
+
Ο
(15)
With
V
RT RT V= ,
nm×
Ο a n-by-m zero matrix,
n
I
the identity n-by-n matrix. The data is given in the
following table using the convention
10
yy
x
xe×=:
Table 2: Engine parameters.
V
R
T
0
c
1
c
2
c
thr
τ
5
2.152e
4
8.279e
−
6
3.041e
−
8
8.5e
−
2
8.35e
−
3
c
0
s
1
s
2
s
0
a
9
2.245e
−
4
7e
−
4
3.9e
−
5
5.78e
−
0.625−
0
b
0
e
0
h
1
h
2
h
59.68 1074− 0
5
1.265e
9
2.145e
The matrix
()
1
r
A
x
denotes the A matrix in
temporal domain during the first phase (i.e.,
crankshaft between 0° and 180°). The third row
expresses, thanks to the coefficient
131
ccx+ , the
phase of intake for the first cylinder. Using the same
logic, it is possible to build three matrices
respectively called
()
2
r
A
t
,
()
3
r
A
t
and
()
4
r
A
t
to
complete the cycle, see Table 1.
As detailed in the previous section, the next step is
to convert this temporal domain into crank-angle
domain (6). Two nonlinearities appear in the system,
1
6
s
nl T n= and
212
(4)
V
nl RT s s x=+. A TS model
based on four rules can be written thanks to the
classical nonlinear sector approach. The two
nonlinearities lead to
2
2 subsystems and are
bounded:
min 1min max
max 1max min
min 2min 1 2 min
max 2 max 1 2 max
600 6
1000 6
0.05 ( )
10 ( )
S
S
V
V
nrpm nlTn
nrpmnlTn
nl RT s s
nl RT s s
αα
αα
==
==
→
=° = +
=° = +
(16)
PeriodicTakagi-SugenoObserversforIndividualCylinderSparkImbalanceinIdleSpeedControlContext
305
As explained before, the premise vector is fully
measured because composed of speed and throttle
angle values. The sample time for the observer can
be considered as
180
s
T =°. Applying Theorem 1 and
using the LMI Toolbox of MATLAB, the observer
gains are obtained from the previous conditions.
This observer can estimate the air mass inside each
cylinder without adding any new sensor.
Two other observers can be built by the same
way: One for the contribution of each cylinder in the
global produced torque, using the following reduced
model:
()
1234
T
T
r prod prod prod prod
xnTTTT=
(17)
()
00
1
45
000
r
ab
Ax
×
=
Ο
,
0
41
r
b
B
×
−
=
Ο
0
41 41
1
,
T
rr
e
CE
××
==
ΟΟ
(18)
The last nonlinear periodic observer can be
used to get the spark advance efficiency. Based on
the two previous presented one, this observer is
constructed with the exactly same methodology as
the other ones. The output of the observer (i.e.,
ˆ
y
) is
the total torque produced by the entire engine (i.e.,
p
rod
T ). The reference torque comes from the second
observer while the first one is used in the C matrix.
The reduced model used to reconstruct the state
vector is the following:
()
1234
T
T
r spk spk spk spk
x TTTT=
(19)
44 41 41
,,ABE
×××
=Ο =Ο =Ο (20)
The C matrix is periodic and based on the equation
from (Balluchi et al., 2010):
p
rod air spk
TTT=⋅
:
()
1
000
air
CT=
(21)
4 SIMULATION RESULTS
This subsection proves the interest of the developed
methodology and the presented periodic nonlinear
observers for detecting imbalance.
Let us start with a nominal scenario (i.e., a
classic stabilization around the speed reference
value, 800 rpm, with neither any disturbance nor any
imbalance, and the spark command set to its optimal
value). The following figures details the speed
(figure 3), the air command (figure 4), the observers
results and their estimation errors (figures 5 to 9)
that converge to 0%.
Figure 3: Stabilized speed around speed reference.
Figure 4: Throttle command in degrees.
Figure 5: Individual cylinder air mass observer results.
To get the observation error, it is necessary to build to
global air mass inside the cylinders, i.e. the air mass used
for the torque calculus. Thanks to the engine speed, we
can select the air mass inside the cylinder which produces
the torque (i.e., the “Expansion” phase in the Table 1).
Figure 6: Air mass observer error in percentage.
0 2 4 6 8 10 12
700
750
800
850
900
time (s)
speed (rpm)
speed
0 2 4 6 8 10 12
2.6
2.8
3
3.2
3.4
3.6
time (s)
throttle command (°)
cmd
thr
0 0.5 1 1.5 2
8.4
8.6
8.8
9
9.2
x 10
-5
time (s)
air mass (kg)
cylinder1
cylinder2
cylinder3
cylinder4
0 2 4 6 8 10 12
-0.1
-0.05
0
0.05
0.1
0.15
time (s)
observer error (%)
obs
air
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
306

Figure 7: Individual cylinder torque observer results.
To get the torque observer error, we have to realize
the same operation as presented before, i.e. using the
engine speed to select only the torque produced by
the cylinder in the “Expansion” phase according to
the Table 1.
Figure 8: Torque observer error in percentage.
By the same way, we can get the spark advance efficiency
thanks to the third observer and build the observation error
using the same idea of selecting only the cylinder in the
“Expansion” phase. Even if a little static error appears, it
stays acceptable (less than 1%)
Figure 9: Individual spark efficiency observer error.
This scenario showed the validity of the designed
periodic nonlinear observers. Let us introduce the
second scenario: An imbalance changes the
behaviour of one or several cylinders. A first
simulation can be realized applying such a
imbalance on the first cylinder. In the engine model,
before the spark efficiency calculus, the spark
advance (i.e., the spark advance command) is
decreased by 20 degrees (i.e., the spark advance
used for the efficiency calculus is
20
spk
cmd −
). For
this scenario, the spark command is set to the
optimal value (i.e.,
26.5
spk
cmd =°
and consequently
20 6.5
spk
cmd −=°
).
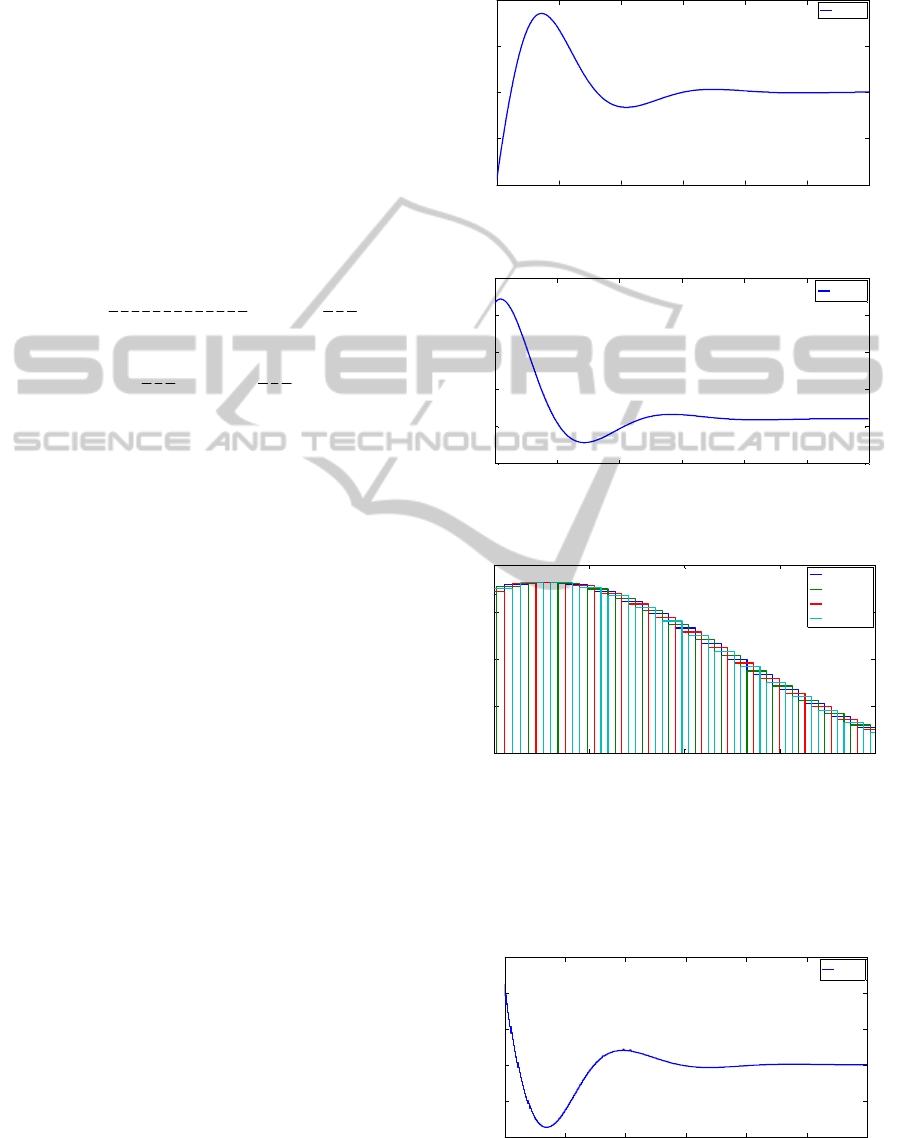
As presented in Figure 13, the spark advance
efficiency observer converges for the first cylinder
to the value of 0.81. Then, using the formula for the
spark efficiency calculus (22) from (Balluchi et al.,
2010), we can return to the spark advance angle.
23
01 2 3
spk
Tvvv v
ϕϕ ϕ
=+ + +
(22)
Applying the inverse of (22), the spark advance
angle
ϕ
corresponding to a
s
pk
T
equal to 0.81 is
6.5°. Comparing to the spark advance command
(26.5°), we can, thanks to the periodic nonlinear
observer, detect an imbalance on the first cylinder
equal to a difference of 20 degrees for the spark
advance.
Figure 10: Individual spark advance efficiency observer
results with an imbalance on Cylinder 1.
Because all the cylinders can suffer from
unbalancing, the next simulation presents the results
for two different imbalances applied on the first and
third cylinders: Their spark advance will be
decreased respectively by 20 and 10 degrees. Figure
14 presents the individual spark advance efficiency
observer results in such a scenario.
Figure 11: Individual spark advance efficiency observer
results with two imbalances.
0 0.2 0.4 0.6 0.8 1
28.6
28.8
29
29.2
29.4
time (s)
Global torque (Nm)
cylinder1
cylinder2
cylinder3
cylinder4
0 2 4 6 8 10 12
-2
-1
0
1
2
time (s)
observer error (%)
obs
T
prod
0 2 4 6 8 10 12
-4
-3
-2
-1
0
1
time (s)
spark efficiency observer error (%)
obs
spk
0 5 10 15 20 25
0.6
0.7
0.8
0.9
1
time
(
s
)
spark efficiency per cylinder (-)
cylinder1
cylinder2
cylinder3
cylinder4
0 1 2 3 4 5 6 7
0.8
0.85
0.9
0.95
1
time
(
s
)
spark efficiency per cylinder (-)
cylinder1
cylinder2
cylinder3
cylinder4
PeriodicTakagi-SugenoObserversforIndividualCylinderSparkImbalanceinIdleSpeedControlContext
307

The spark advance efficiency observer converges to
the optimal value, 1, for Cylinders 2 and 4. Cylinder
1 converges to the same value as Figure 12, 0.81,
and Cylinder 3 converges to 0.94. Using the inverse
of (22), the following spark advance degrees and
imbalances can be identified:
1
2
3
4
6.5
Imbalance : 20
26.5
0
16.5
10
26.5
0
ϕ
ϕ
ϕ
ϕ
=°
−°
=°
−°
→
=°
−°
=°
−°
(23)
5 CONCLUSIONS
This paper has presented a methodology to
manipulate hybrid dynamic systems as periodic
models and adapt them to crank-angle domain. Such
an adaptation can lead to the construction of a
periodic nonlinear Takagi-Sugeno representation,
allowing using efficient tools such as LMI. Thanks
to this methodology, this paper presents how to build
periodic TS observers and demonstrates with
examples such as individual cylinder air mass,
global produced torque or individual cylinder spark
advance efficiency, allowing the detection of an
imbalance between the cylinders. This can lead to a
tuned spark advance control, including auto-
balancing of the cylinders.
ACKNOWLEDGEMENTS
This research is sponsored by the International
Campus on Safety and Intermodality in
Transportation the Nord-Pas-de-Calais Region, the
European Community, the Regional Delegation for
Research and Technology, the Ministry of Higher
Education and Research, and the French National
Center for Scientific Research (CNRS).
REFERENCES
Balluchi, A., D’Apice, C., Gaeta, M., Piccoli, B.,
Sangiovanni Vincentelli, A. L., and Zadarnowska, K.
(2010). A hybrid feedback for a benchmark problem
of idle speed control.
International Journal of Robust
and Nonlinear Control
20, 515–530.
Bengea, S. C., Li, X., and DeCarlo, R. A. (2004).
Combined Controller-Observer Design for Uncertain
Time Delay Systems With Application to Engine Idle
Speed Control. Journal of Dynamic Systems,
Measurement, and Control
126, 772–780.
Bittanti, S., and Colaneri, P. (2000). Invariant
representations of discrete-time periodic systems.
Automatica 36, 1777–1793.
Bohn, C., Bohme, T., Staate, A., and Manemann, P.
(2006). A nonlinear model for design and simulation
of automotive idle speed control strategies. in
American Control Conference (IEEE), 3272–3277.
Bolzern, P., Colaneri, P., and Scattolini, R. (1986). Zeros
of discrete-time linear periodic systems. IEEE
Transactions on Automatic Control
31, 1057–1058.
Di Cairano, S., Yanakiev, D., Bemporad, A.,
Kolmanovsky, I. V., and Hrovat, D. (2008). An MPC
design flow for automotive control and applications to
idle speed regulation. in
Conference on Decision and
Control
(IEEE), 5686–5691.
Di Cairano, S., Yanakiev, D., Bemporad, A.,
Kolmanovsky, I. V., and Hrovat, D. (2011). Model
Predictive Idle Speed Control: Design, Analysis, and
Experimental Evaluation. IEEE Transactions on
Control Systems Technology
20, 84–97.
Chauvin, J., Corde, G., Petit, N., and Rouchon, P. (2007).
Periodic input estimation for linear periodic systems:
Automotive engine applications.
Automatica 43, 971–
980.
Di, N., Kai, S., Junhui, H., and Jiajun, S. (2010).
Individual Spark Advance Adjusting in a Multi-
Cylinder Spark Ignition Engine. in International
Conference on Electrical and Control Engineering
(IEEE), 1192–1195.
Grizzle, J. W., Dobbins, K. L., and Cook, J. A. (1991).
Individual cylinder air-fuel ratio control with a single
EGO sensor. IEEE Transactions on Vehicular
Technology
40, 280–286.
Guerra, T.-M., Kerkeni, H., Lauber, J., and Vermeiren, L.
(2012). An efficient Lyapunov function for discrete T–
S models: observer design.
IEEE Transactions on
Fuzzy Systems
20, 187–192.
Kerkeni, H., Lauber, J., and Guerra, T. M. (2010).
Estimation of Individual In-cynlinder air mass flow
via Periodic Observer in Takagi-Sugeno form. in
IEEE
Vehicle Power and Propulsion Conference
(IEEE), 1–
6.
Kerkeni, H., Lauber, J., and Guerra, T.-M. (2009). Some
results about stabilization of periodic takagi-sugeno
models. in
IEEE International Conference on Fuzzy
Systems
(IEEE), 814–819.
Lendek, Z., Guerra, T.-M., Babuška, R., and De Schutter,
B. (2010). Stability analysis and nonlinear observer
design using Takagi-Sugeno fuzzy models
. Berlin:
Springer.
Lendek, Z., Lauber, J., and Guerra, T.-M. (2013a).
Periodic Lyapunov functions for periodic TS systems.
Systems & Control Letters 62, 303–310.
Lendek, Z., Lauber, J., and Guerra, T. M. (2012).
Switching Lyapunov functions for periodic TS
systems. in
Embedded Systems, Computational
Intelligence and Telematics in Control
, 102–107.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
308

Lendek, Z., Lauber, J., Guerra, T.-M., and Raica, P.
(2013b). On stabilization of discrete-time periodic TS
systems. in IEEE International Conference on Fuzzy
Systems
(IEEE).
De Santis, E., Di Benedetto, M. D., and Pola, G. (2006).
Digital idle speed control of automotive engines: A
safety problem for hybrid systems.
Nonlinear
Analysis: Theory, Methods & Applications
65, 1705–
1724.
Shamekhi, A. H., and Ghaffari, A. (2005). Fuzzy control
of spark advance by ion current sensing. SAE
Technical Paper.
Takagi, T., and Sugeno, M. (1985). Fuzzy identification of
systems and its applications to modeling and control.
IEEE Transactions on Systems, Man, and Cybernetics,
116–132.
Tanaka, K., and Wang, H. O. (2001). Fuzzy control
systems design and analysis a linear matrix inequality
approach
. New York: Wiley.
Tuan, H. D., Apkarian, P., Narikiyo, T., and Yamamoto,
Y. (2001). Parameterized linear matrix inequality
techniques in fuzzy control system design.
IEEE
Transactions on Fuzzy Systems
9, 324–332.
Yildiz, Y., Annaswamy, A., Yanakiev, D., and
Kolmanovsky, I. (2007). Adaptive idle speed control
for internal combustion engines. in
American Control
Conference
(IEEE), 3700–3705.
Yurkovich, S., and Simpson, M. (1997). Comparative
analysis for idle speed control: a crank-angle domain
viewpoint. in
American Control Conference (IEEE),
278–283.
PeriodicTakagi-SugenoObserversforIndividualCylinderSparkImbalanceinIdleSpeedControlContext
309
