New Results for Partial Key Exposure on RSA with Exponent Blinding

Stelvio Cimato

, Silvia Mella

and Ruggero Susella

Universit`a degli Studi di Milano, Milano, Italy

STMicroelectronics, Agrate Brianza, Italy

Keywords:

RSA, Partial Key Exposure, Coppersmith’s Method, Exponent Blinding, Horizontal Attack.

Abstract:

In 1998, Boneh, Durfee and Frankel introduced partial key exposure attacks, a novel application of Copper-

smith’s method, to retrieve an RSA private key given only a fraction of its bits. This type of attacks is of

particular interest in the context of side-channel attacks. By applying the exponent blinding technique as a

countermeasure for side-channel attacks, the private exponent becomes randomized at each execution. Thus

the attacker has to rely only on a single trace, signiﬁcantly incrementing the noise, making the exponent bits

recovery less effective. This countermeasure has also the side-effect of modifying the RSA equation used

by partial key exposure attacks, in a way studied by Joye and Lepoint in 2012. We improve their results by

providing a simpler technique in the case of known least signiﬁcant bits and a better bound for the known most

signiﬁcant bits case. Additionally, we apply partial key exposure attacks to CRT-RSA when exponent blinding

is used, a case not yet analyzed in literature. Our ﬁndings, for which we provide theoretical and experimental

results, aim to reduce the number of bits to be recovered through side-channel attacks in order to factor an

RSA modulus when the implementation is protected by exponent blinding.

1 INTRODUCTION

At Eurocrypt 1996 Don Coppersmith presented a

novel method to ﬁnd small solutions of univariate

modular polynomials, with some applications to the

RSA cryptosystem (Coppersmith, 1996b). He ex-

tended the method to bivariate equations, which al-

lowed to factor an RSA modulus given half of the bits

of one of its prime factors (Coppersmith, 1996a).

In 1998, Boneh, Durfee and Frankel introduced

partial key exposure, a family of attacks on RSA re-

quiring the knowledge of some consecutive most sig-

niﬁcant bits (MSB) or least signiﬁcant bits (LSB)

of the private exponent (Boneh et al., 1998). The

main idea behind their methods, for the common

cases where the factorization of the public exponent

is known, is to use the given partial information on

the private exponent to obtain partial information on

a prime factor of the modulus, and then apply Cop-

persmith’s method to factor.

This application is of high interest in the context

of side-channel attacks. Side-Channel attacks, intro-

duced in 1996 by Paul Kocher (Kocher, 1996), are

attacks on physical implementations of cryptographic

algorithms. In these attacks a side-channel informa-

tion of the computation (such as power consumption,

electromagnetic emission, acoustic emission, etc.) is

used to recover the secret used during the computa-

tion.

Most side channel attacks leverage on combining

the side-channel leakages, i.e. traces, of several exe-

cutions of the cryptographic algorithm with same se-

cret but different input. The ﬁrst attack of this family

is Differential Power Analysis (DPA) (Kocher et al.,

1999). Its main feature is the ability to signiﬁcantly

reduce the random noise, by averaging a large amount

of traces, compared to Simple Power Analysis (SPA),

where only one trace is used.

The reader may now wonder why an attacker

might be able to obtain information on a part of the

secret exponent and not on the entire exponent. The

reason is that some countermeasures can be adopted

by implementers to thwart side channel attacks.

A common countermeasure used for RSA is expo-

nent blinding, originally introduced in (Kocher, 1996)

but often attributed to (Coron, 1999). It consists of

adding a random multiple of φ(N) to the RSA pri-

vate exponent at each execution. This countermea-

sure has the feature to change the private exponent at

each computation, thus not permitting the use of mul-

tiple traces, as required for DPA. This results in the

need of using a single trace to discover the secret key.

136

Cimato S., Mella S. and Susella R..

New Results for Partial Key Exposure on RSA with Exponent Blinding.

DOI: 10.5220/0005571701360147

In Proceedings of the 12th International Conference on Security and Cryptography (SECRYPT-2015), pages 136-147

ISBN: 978-989-758-117-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

A method for this was originally proposed in (Walter,

2001), for a particular exponentiation algorithm, and

generalized for regular exponentiation algorithms in

(Clavier et al., 2010) and named horizontal attack.

The practical issue that the adversary faces in the

horizontal setting is the high noise. Therefore, the ad-

versary is able to correctly guess only a partial num-

ber of the bits of the exponent and not the entire ex-

ponent.

The application of partial key exposure, when ex-

ponent blinding is used as side-channel countermea-

sure, would allow the imperfect attacker to still re-

cover the correct private exponent. However, the

equation exploited by Boneh, Durfee and Frankel is

modiﬁed by the introduction of exponent blinding and

their attacks don’t apply anymore.

The question as to whether partial key exposure

could be applied in this setting was answered in (Joye

and Lepoint, 2012). The authors presented two tech-

niques to recover the full exponent, knowing enough

MSB or LSB portions of it, leaving the open question

as up to which extent it is possible to apply partial

key exposure when exponent blinding is applied to

the CRT variant of RSA (Quisquater and Couvreur,

1982).

Our contribution consists of new methods for par-

tial key exposure when exponent blinding is used, im-

proving the results of (Joye and Lepoint, 2012) for

common RSA settings and providingnovelattacks for

the CRT variant. Speciﬁcally, in this work, we:

• reduce the number of required bits for the MSB at-

tack and make it to not rely on a common heuristic

assumption;

• provide a more efﬁcient technique for the LSB at-

tack, requiring to reduce a lattice basis of lower

dimension;

• present novel attacks against CRT-RSA imple-

mentations that make use of exponent blinding.

This particular case has never been analyzed be-

fore.

This work is organized as follows. In Section 2 we

recall some basic information about RSA. In Sec-

tion 3 we give a brief introduction about lattices and

Coppersmith’s method. In Section 4 we present two

partial key exposure attacks on RSA with exponent

blinding and in Section 5 on CRT-RSA with exponent

blinding. Experimental results are then provided in

Section 6.

2 RSA APPLICATIONS

In literature, Coppersmith’s method has been applied

with very different, and unusual, RSA parameters.

For example the case where e is of the same bitsize

of N has been analyzed in (Ernst et al., 2005). In this

work we preferred to focus our analysis on more com-

mon RSA settings.

Let (N,e) be a RSA public key. The modulus N =

pq has prime factors p and q of equal bit-size. We

assume wlog that p > q, that implies

q <

√

N < p < 2q < 2

√

and

√

N < p+ q < 3

√

It is common practice to choose 1024 or 2048-bit

modulus N.

The most common value for the public exponent e

is 2

+ 1. This is also the default value for the pub-

lic exponent in the OpenSSL library. Other common

values are 3 and 17. NIST mandates that e satisﬁes

< e < 2

256

(Kerry et al., 2013). Therefore, to be as

generic as possible but still adhering to realistic sce-

narios, we will consider in our analysis 3 ≤ e < 2

256

but we will provide experiments only for the most

common case e = 2

+ 1.

The private exponent d satisﬁes ed −1 = kφ(N)

for some integer k, where φ(N) denotes the Euler to-

tient function. The exponent d is commonly chosen

to be full size, namely as large as φ(N). In order to

speed-up the decryption process, someone suggests

to use smaller d. However, this choice may lead to

security problems as Wiener’s attack (Wiener, 1990).

Therefore, it is usually avoided.

The side-channel countermeasure considered in

this work is the exponent blinding introduced by

Kocher (Kocher, 1996). It consists of adding a ran-

dom multiple of φ(N) to d, thus RSA exponentia-

tion is computed by using the new exponent d

∗

d + ℓφ(N), for some ℓ > 0. The dimension of ℓ is a

tradeoff between security and efﬁciency. If ℓ is 32-bit

long or smaller, it allows some combination of brute-

forcing and side-channel as in (Fouque et al., 2006),

where a brute-force on ℓ is required. Thus, it is a safer

choice to use ℓ with bit-size 64. A larger dimension

would make the decryption process less efﬁcient.

In our analysis, to maintain generality, we will

consider 0 ≤ ℓ < 2

128

and in our experiments we will

test bit-sizes of 0, 10, 32, 64 and 100. Our methods

never require the capability of brute-forcing the val-

ues of k or ℓ, sometimes needed in other works.

In order to speed up the exponentiation compu-

tation, some RSA implementations make use of a

technique based on the Chinese Remainder Theorem

(CRT). In particular, one can use exponents

= d mod (p−1) and d

= d mod (q−1)

to compute

mod p and x

mod q.

NewResultsforPartialKeyExposureonRSAwithExponentBlinding

137

Then, the two results can be combined using the CRT

to obtain x

mod N (Quisquater and Couvreur, 1982).

Also CRT-RSA can be protected with exponent

blinding. Thus, exponentiation is computed by using

∗

= d

+ℓ

(p−1) and d

∗

= d

+ℓ

(q−1), for some

ℓ

,ℓ

> 0.

In this work we will consider both RSA and CRT-

RSA implementations that make use of the exponent

blinding countermeasure. Our RSA settings will con-

sider moduli of 1024 and 2048 bits, public exponent

such that 3 ≤ e < 2

256

, private exponent of full size

and a randomization factor up to 128 bits.

To derive theoretical bounds in next sections, we

prefer to express the restrictions on e and ℓ with re-

spect to the modulus N. In general, we translate

them to the less restrictive conditions: ℓ < 2N

and

e < 2N

. When necessary, we will consider more re-

strictive bounds.

We will run experiments by considering the

widely used public exponent e = 2

+ 1 and random

values ℓ of different bit-size from 0 to 100. The mod-

ulus N will be 2048-bit long, but note that our attacks

are effective also for other sizes.

3 GENERAL STRATEGY

Partial key exposure attacks relies on Coppersmith’s

method for ﬁnding roots of modular polynomials and

multivariate polynomials. This method makes signif-

icant use of lattices and lattice reduction algorithms.

We give here a brief introduction to lattices and

to the general strategy used in partial key exposure

attacks and thus also in our attacks.

3.1 Lattices

Given a set of real linearly independent vectors

B = {b

,..., b

} with b

∈ R

, a (full-rank) lattice

spanned by B is the set of all integer linear com-

binations of vectors of B. Namely, the set L(B) =

{

∑

: x

∈ Z}.

B is called the basis of the lattice and the (n ×

n)-matrix consisting of the row vectors b

,..., b

called basis matrix.

Every lattice has an inﬁnite number of lattice

bases. A basis is obtained from another through a uni-

modular transformation (i.e., by multiplying the basis

matrix by a matrix with determinant ±1). The deter-

minant of the lattice is deﬁned as det(L) = |det(B

and is an invariant, namely it is independent of the

choice of the basis. The dimension of the lattice is

dim(L) = n.

The goal of lattice reduction is to ﬁnd a basis with

short and nearly orthogonal vectors. The LLL algo-

rithm (Lenstra et al., 1982) produces in polynomial

time a set of reduced basis vectors. The following

theorem bounds the norm of these vectors.

Theorem 1 (Lenstra-Lenstra-Lov´asz). Let L be a lat-

tice of dimension n. The LLL-algorithm outputs in

polynomial time reduced basis vectors v

, 1 ≤ i ≤ n,

satisfying

k ≤ kv

k ≤ ... ≤ kv

k ≤ 2

n(n−1)

4(n+1−i)

detL

n+1−i

3.2 General Strategy

In (Coppersmith, 1996b), Don Coppersmith presents

a rigorous method to ﬁnd small roots of univariate

modular polynomials. The method is based on LLL

and can be extended to polynomialsin more variables,

but only heuristically.

In this work we use the following reformulation

of Coppersmith’s theorem due to Howgrave-Graham

(Howgrave-Graham, 1997).

Theorem2 (Howgrave-Graham). Let f(x

,...,x

) be

a polynomial in k variables with n monomials. Let m

be a positive integer. Suppose that

1. f(r

,...,r

) = 0 mod b

where |r

| < X

∀i

2. kf(x

,..., x

)k <

√

Then f(r

,..., r

) = 0 holds over the integers.

The general strategy is the following. Starting

from an RSA equation we construct a multivariate

polynomial f

,..., x

) modulo an integer b, such

that its root (r

,..., r

) contains secret values. Our

goal is to ﬁnd this root, even if no classic root ﬁnd-

ing method is known for modular polynomials. So,

we construct k polynomials f

,..., f

satisfying the

two conditions of Theorem 2 so that such polynomi-

als will have the same root (r

,..., r

) over Z. Finally,

we compute the common roots of these polynomials

and recover the secret values.

To generate such polynomials we apply the fol-

lowing strategy. Starting from f

we construct auxil-

iary polynomials g

,..., x

) that all satisfy condi-

tion 1 of Howgrave-Graham’s Theorem. Since every

integer linear combination of these polynomials also

satisﬁes condition 1, we look for linear combinations

that also satisfy condition 2. Such combinations are

the polynomials f

,..., f

In order to construct f

,..., f

, we build a lattice

L(B) where the basis B is composed by the coefﬁcient

vectors of the polynomials g

,..., x

) (with

,..., X

bounds on the root as in Theorem 2).

SECRYPT2015-InternationalConferenceonSecurityandCryptography

138

By using the LLL-lattice reduction algorithm, we

obtain a reduced basis for the lattice L as in Theorem

1. The ﬁrst k vectors of the reduced basis have norm

smaller than

√

, if:

n(n−1)

4(n+1−k)

detL

n+1−k

√

We may let terms that do not depend on N contribute

to an error term ε and consider the simpliﬁed condi-

tion

detL ≤ b

m(n+1−k)

. (1)

If this condition holds, then we can use the ﬁrst k

reduced-basis vectors to construct the polynomials

,..., f

satisfying the second condition of Theorem

2. Then, in order to compute (r

,..., r

), we do the

following.

If k = 1, then we consider the polynomial F =

) and apply a classic roots ﬁnding algorithm for

univariate polynomials over the integers.

If k > 1, we use the resultant computation to con-

struct k univariate polynomials F

) from f

,..., f

and apply a classic roots ﬁnding algorithm for each of

them. The effectiveness of this last method relies on

the following heuristic assumption.

Assumption 1. The resultant computation for the

polynomials f

described above yields a non-zero

polynomial.

This assumption is fundamental and widely used

for many attacks in literature (Joye and Lepoint, 2012;

Lu et al., 2014; Bl¨omer and May, 2003; Boneh et al.,

1998; Ernst et al., 2005). None of our experiments has

ever failed to yield a non-zero polynomial and hence

to mount the attack.

In this work we will make use of a seminal result

due to Coppersmith, based on the strategy described

above. We present here a more general variant of it,

due to May (May, 2003), together with a sketch of its

proof to illustrate how we will construct lattices for

our experiments.

Theorem 3. Let N = pq with p > q. Let k be an

unknown integer that is not a multiple of q. Suppose

we know an approximation

kp of kp with |kp−

kp| ≤

. Then we can factor N in time polynomial in

logN.

Sketch of proof. Deﬁne the univariate polynomial

(x) = x+

with root x

= kp−

kp modulo p.

Divide the interval [−2N

,2N

] into 8 subintervals

of size

centered at some x

For each subinterval consider the polynomial f

(x −

) and ﬁnd its roots r such that |r| ≤

. Among all

these roots of all these polynomials there is also x

So, for each f

(x − x

) set X =

. Fix m =

⌈logN/4⌉ and set t = m.

Deﬁne the auxiliary polynomials

i, j

(x) = x

m−i

for i = 0, . . .,m−1; j = 0

(x) = x

(x) for i = 0,. . . ,t −1

and construct the lattice spanned by the vectors

i, j

(xX) and h

(xX).

By applying the LLL-algorithm to L, a reduced ba-

sis is obtained. From the shortest vector construct the

polynomial f

(x). Among its roots over the integers,

there are also the roots of f

(x −x

). Compute the

roots of f

(x) by using a classic roots-ﬁnding algo-

rithm.

Construct the set R of all integer roots of the polyno-

mials f

(x). The set R will contain also the root x

Thus, f(x

) = kp can be computed and, since k is not

a multiple of q, the computation of gcd(N,kp) gives

Recall that the LLL-algorithmis polynomial in the

dimension of the matrix basis and in the bit-size of its

entries. Since the dimension of the lattice is m + t =

⌈logN/2⌉ and the bit-size of its entries is bounded by

a polynomial in (mlogN), every step of the proof can

be done in polynomial time.

4 ATTACKS ON RSA

In this section we present two attacks on RSA imple-

mentations, one given the most signiﬁcant bits of the

private exponent and the other one given its last sig-

niﬁcant bits. We assume that the private exponent d is

full-size and that it is masked by a random multiple ℓ

of φ(N). Thus, exponentiation is performed by using

the exponent d

∗

= d + ℓφ(N) for some ℓ ≥ 0. When

ℓ = 0 clearly d

∗

= d, that means that no countermea-

sure is applied.

Joye and Lepoint presented partial key exposure

attacks on RSA with exponent blinding (Joye and Le-

point, 2012). Here we present two alternative ap-

proaches that allow us to get better bounds on the

number of leaked bits necessary to the attacker to

break the system.

4.1 Partial Information on LSB of d

∗

In this section, we assume that the attacker is able to

recover the least signiﬁcant bits of the secret d

∗

. We

write d

∗

= d

·M + d

, where d

represents the frac-

tion of d

∗

known to the attacker while d

represents

NewResultsforPartialKeyExposureonRSAwithExponentBlinding

139

the unknown part. For instance, if the attacker knows

the m LSB of d

∗

, then M = 2

We prove that if the attacker knows a sufﬁciently

large number of least signiﬁcant bits, then she can fac-

tor N.

To prove our result, we generalize the method

used in (Bl¨omer and May, 2003), by introducing the

new factor ℓ.

Theorem 4. Let (N,e) be an RSA public key with e =

≤ 2N

and d

∗

= d + ℓφ(N), for some ℓ = N

≤

. Suppose we are given d

and M satisfying d

∗

mod M with

M ≥ N

√

1+6(α+σ)+

(1+6σ)+ε

for some ε > 0. Then, under Assumption 1, we can

ﬁnd the factorization of N in time polynomial in logN.

Proof. We start from the RSA equation

ed −1 = kφ(N).

Since d

∗

= d + ℓφ(N), we obtain the equation

∗

−1 = (k + eℓ)φ(N).

Let k

∗

= k+ eℓ, so that ed

∗

−1 = k

∗

φ(N).

By writing d

∗

= d

M + d

and considering that

φ(N) = N −(p+ q −1), we get

∗

N −k

∗

(p+ q −1) −ed

+ 1 = eMd

It follows that the bivariate polynomial

(x,y) = xN −xy −ed

+ 1

has root (x

) = (k

∗

, p + q−1) modulo eM.

In order to bound x

, notice that

∗

−1

φ(N)

< e



d + ℓφ(N)

φ(N)



< e(1+ ℓ) ≤2N

α+σ

In addition, recall that p + q ≤ 3N

We can set the bounds X = 2N

α+σ

and Y = 3N

that x

≤ X and y

≤Y.

To construct the lattice, we consider the following

auxiliary polynomials

i, j

(x,y) = x

(eM)

m−i

for i = 0, . . . ,m; j = 0,...,i

i, j

(x,y) = y

(eM)

m−i

for i = 0, . . . , m; j = 1, . . . ,t

for some integers m and t, where t = τm has to be op-

timized.

All integer linear combinations of these polynomials

have the root (x

) modulo (eM)

, since they all

have a term (eM)

m−i

. So the ﬁrst condition of The-

orem 2 is satisﬁed. In order to satisfy the second con-

dition, we have to ﬁnd a short vector in the lattice

spanned by g

i, j

(xX,yY) and h

i, j

(xX,yY). In particu-

lar, this vector shall have a norm smaller than

(eM)

√

dimL

The second condition of Theorem 2 is satisﬁed when

inequality (1) holds, i.e. if

detL ≤ (eM)

m(n−1)

. (2)

An easy computation shows that n =



τ+



and

that

detL(M) =



(eMY)

3τ+2

3τ

+3τ+1



(1+o(1))

Considering the bounds X = 2N

α+σ

andY = 3N

, we

obtain the condition



(eM2N

α+σ

)

3τ+2

(3N

)

3τ

+3τ+1



(1+o(1))

≤(eM)

m(n−1)

that reduces to

(

(α+σ)(3τ+2)+

(3τ

+3τ+1)

)

(1+o(1))

≤ (eM)

m(n−1)−

(3τ+2)(1+o(1))

We know that eM ≥N

√

1+6(α+σ)+

(1+6σ)+ε

, so the

above condition is satisﬁed if

9τ

+6(α+σ+τ)−2

1+ 6(α+ σ)(1+3τ)+2≤0.

The left-hand side is minimized, for

τ =



1+ 6(α+ σ)−1



Thus, for this choice of τ condition 2 is satisﬁed so

we can successfully apply the LLL-algorithm.

From the LLL-reduced basis, we construct two

polynomials f

(x,y), f

(x,y) with the common root

) over the integers. By the heuristic assump-

tion, the resultant res

( f

, f

) is not zero and we can

ﬁnd y

= p + q −1 using standard root ﬁnding algo-

rithms. This gives us the factorization of N.

To conclude the proof, we need to show that every

step of the method can be done in time polynomial in

log(N). The LLL-algorithm runs in polynomial time,

since the basis matrix B has constant dimension (ﬁxed

by m) and its entries are bounded by a polynomial

in N. Additionally, res

( f

, f

) has constant degree

and coefﬁcients bounded by a polynomial in N. Thus,

every step can be done in polynomial time.

We would like to make two considerations. The

ﬁrst is that when σ = 0, we get the same result of

(Bl¨omer and May, 2003). Indeed, our method is a

generalization of it. The second is that we obtain the

same bound of (Joye and Lepoint, 2012), but our ap-

proach is more effective in practice. As we will show

in Section 6.1, we are able to get closer to the theoret-

ical bound by using smaller lattices.

SECRYPT2015-InternationalConferenceonSecurityandCryptography

140

4.2 Partial Information on MSB of d

∗

In this section, we prove that if the attacker knows a

sufﬁciently large number of most signiﬁcant bits of

the protected exponent, then she can factor N.

To prove this result, we show how the partial

knowledge on d

∗

can be used to construct an approx-

imation of p that allows to apply Theorem 3.

The advantage of this approach compared to (Joye

and Lepoint, 2012) is that it does not rely on the

heuristic assumption 1 and yields to a better bound.

Theorem 5. Let (N,e) be an RSA public key with

e = N

and d

∗

= d + ℓφ(N) for some ℓ = N

with

σ > 0 and N

α+σ

< 2N

. Suppose that |p−q|≥ cN

for some c ≤

, and suppose we are given an approx-

imation

∗

of d

∗

such that

∗

−

∗

| ≤ cN

+σ

Then we can ﬁnd the factorization of N in time poly-

nomial in logN.

Notice that, like in Theorem 4, we have ed

∗

−1 =

∗

φ(N) with k

∗

= k+ eℓ.

In order to prove Theorem 5 we need ﬁrst to prove

the following lemma.

Lemma 1. With N

α+σ

< 2N

, given

∗

such that

∗

−

∗

| ≤

1−α

then the approximation

∗

−1

N+1

of k

∗

is exact.

Proof. This proof follows the same strategy used in

the proof of Theorem 6 of (Bl¨omer and May, 2003).

Note that

∗

−

∗

| <



∗

−1

φ(N)

−

∗

−1

N + 1



(ed

∗

−1)(N + 1) −(e

∗

−1)(N + 1−(p + q))

φ(N)(N + 1)



Then, given that φ(N) > N/2, p+ q ≤3N

, N

+N >

and d

∗

< 2N

1+σ

, we obtain

∗

−

∗

| <



e(d

∗

−

∗

)

φ(N)



(p+ q)(e

∗

−1)

φ(N)(N + 1)



1−α



+α+1+σ

(N + 1)



+ 12N

−

With RSA parameters, we have 12 ≪ N

1/8

, so we can

safely assume |k

∗

−

∗

| < 1. But the difference be-

tween two integers is an integer, thus we can conclude

that it is zero, therefore

∗

= k

∗

It is worth to observe two facts: ﬁrst, the bound

∗

−

∗

| ≤

1−α

requires the attacker to get the

(log

σ+α

) + 2) most signiﬁcant bits of d

∗

, a result

which holds even for σ = 0 (i.e. d

∗

= d); second, the

assumption N

α+σ

< 2N

of Lemma 1 always holds

for our choice of RSA parameters.

We can now prove Theorem 5.

Proof of theorem 5. We begin by applying Lemma 1

to obtain the value of k

∗

. The condition |d

∗

−

∗

| ≤

1−α

of the lemma is always satisﬁed by our choices

of RSA parameters because

+σ

≪

1−α

, since

< 2N

and N

< 2N

We can deﬁne an approximation ˜s of s = p + q as

˜s := 1+ N −

∗

−1

∗

Reminding that k

∗

, with the assumption of σ > 0, is

lower bounded by N

α+σ

, we obtain

|s− ˜s|=



∗



∗

−

∗





≤

α+σ

+σ

≤ cN

We use ˜s to deﬁne

˜p :=



˜s+

˜s

−4N



as an approximation of p.

Without loss of generality, following Appendix B of

(Boneh et al., 1998), we now assume that ˜s ≥ s, so

that ˜p ≥ p.

Observe that

˜p− p =

( ˜s−s) +



˜s

−4N −

−4N



( ˜s−s) +

( ˜s+ s)( ˜s−s)



√

˜s

−4N +

√

−4N



Since ˜s ≥ s, we have ˜s

−4N ≥ s

−4N = (p −q)

and |p −q|≥ cN

with c ≤

Noting that ˜s ≤ s+ cN

, we have

˜s+s ≤2s+cN

≤2(p+q)+N

≤6N

≤7N

It follows that

˜p− p ≤

( ˜s−s) +

( ˜s+ s)( ˜s−s)

4(p −q)

≤

(7N

)(cN

)

4cN

≤

≤ 2N

Since the approximation ˜p satisﬁes the hypothesis

of Theorem 3 with k = 1, we can ﬁnd the factorization

of N in time polynomial in logN.

NewResultsforPartialKeyExposureonRSAwithExponentBlinding

141

From Theorem 5 we can recover the minimum

number of known MSB bits required. In accordance

to previous sections we deﬁne this quantity as log

where M is deﬁned as

M =

∗

−

∗

1+σ

+σ

= 4N

. (3)

It is important to underline that this bound is not af-

fected by the size of α and σ as long as the con-

dition of Lemma 1 holds. In fact, while it might

seem counter-intuitive, the presence of the counter-

measure (i.e. σ > 0) improves the theoretical bound

|d −

d| ≤ cN

−α

of Theorem 3.3 of (Boneh et al.,

1998). However, this difference was not shown in the

experimental results, probably due to low value of α

when e = 2

+ 1.

Also note that Theorem 5 provides a signiﬁcant

improvement over the bound of (Joye and Lepoint,

2012). In fact, for α+ σ ≤

(which is always true in

our setting), their bound is |d

∗

−

∗

| ≤ N

α+σ

, which

would require knowledge of log

1−α

) bits.

Attack using both MSB and LSB of d

∗

We want to

brieﬂy analyze also the case where the attacker might

be able to detect bits in different positions of d

∗

. In

this scenario, the attacker could obtain enough most

signiﬁcant bits to satisfy Lemma 1 and obtain

log

least signiﬁcant bits to recover half of the bits of p and

factor N, as shown in (Boneh et al., 1998). Thus, the

knowledge of only (log

+σ+α

) + 2 + ε) bits and

the resolution of an univariate equation are required.

We don’t describe the attack in details because, once

∗

is recovered applying Lemma 1, it reduces to the

method of (Boneh et al., 1998). Thus, we remind the

reader to it. In Section 6, we will provide experimen-

tal results.

5 ATTACKS ON CRT-RSA

In this section we present two attacks on CRT-RSA

implementations, where we target exponentiation by

∗

. One is based on the knowledge of the most sig-

niﬁcant bits of the CRT private exponent and one is

based on the knowledge of its least signiﬁcant bits.

We assume that the private exponent d

is full-size

(with respect to p) and that it is masked by a random

multiple ℓ of (p −1), for some ℓ ≥ 0. When ℓ = 0

clearly d

∗

= d

, that means that no countermeasure is

applied.

5.1 Partial Information on LSB of d

∗

In this section, we assume that the attacker is able to

recover the least signiﬁcant bits of the secret d

∗

. We

can write d

∗

= d

·M+d

where d

is known to the at-

tacker while d

is unknown. The integer M is a power

of two and represents the bound on the known part.

We prove that if the attacker knows a sufﬁciently

large number of least signiﬁcant bits, then she can fac-

tor N.

To prove our result we use a method presented by

Herrmann and May to ﬁnd the solutions of a bivariate

linear equation modulo p (Herrmann and May, 2008).

Theorem 6. Let (N,e) be an RSA public key with e =

. Let d

= d mod p−1 and let d

∗

= d + ℓ(p −1)

for some ℓ = N

with σ ≥ 0. Suppose that N

α+σ

≤

√

−

and that we are given d

and M satisfying

= d

∗

mod M with

M ≥ N

1−

√

+α+2σ+ε

for some ε > 0. Then, under Assumption 1, we can

ﬁnd the factorization of N (in time polynomial in

logN).

Proof. We start from the equation

−1 = k

(p−1).

Since d

∗

= d

+ ℓ(p−1), we obtain

∗

−1 = (k

+ eℓ)(p−1).

Let k

∗

denote k

+ eℓ. By writing d

∗

= d

M + d

, we

obtain the following equation

eMd

+ k

∗

+ ed

−1 = k

∗

It follows that the bivariate polynomial

(x,y) = eMx+ y+ ed

−1

has root (x

) = (d

∗

) modulo p.

In order to bound y

, notice that

∗

−1

(p−1)

< e



+ ℓ(p−1)

(p−1)



< e(1+ ℓ) ≤ 2N

α+σ

Additionally, recall that d

∗

−d

We can set bounds X = N

√

−

−α−σ

and Y = 2N

α+σ

so that x

≤ X and y

≤Y.

To construct the lattice, we consider the following

auxiliary polynomials:

f = x+ Ry+ R(ed

−1) where R = (eM)

−1

mod N

k,i

= y

max{t−k,0}

, k = 0,...,m;i = 0,... , m−k

for some integers m and t, where t = τm has to be

optimized.

SECRYPT2015-InternationalConferenceonSecurityandCryptography

142

All integer linear combinations of these polyno-

mials share the root (x

) modulo p

. Thus, the ﬁrst

condition of Theorem 2 is satisﬁed. In order to satisfy

the second condition we have to ﬁnd a short vector in

the lattice L, spanned by g

k,i

(xX,yY). In particular,

this vector shall have a norm smaller than

√

dimL

The second condition of Theorem 2 is satisﬁed

when equation (1) holds, i.e. when

detL ≤ N

τm(n−1)

. (4)

A straightforward computation shows that n =

+ 3m + 2) and that

detL(M) = (XY)

+3m

+2m)

mτ(mτ+1)(4+3m−mτ)

Thus, condition (4) becomes

(XY)

+3m

+2m)

≤ N

τm(m

+3m)−

mτ(mτ+1)(4+3m−mτ)

that reduces to

XY ≤ N

(3τ+2τ

−6τ

)

Since XY = 2N

√

−

, the above condition is satisﬁed

√

−

(3τ+ 2τ

−6τ

) ≤ 0.

The left-hand side is minimized for τ = 1−

√

. For

this choice of τ condition (4) is satisﬁed, so we can

successfully apply LLL-algorithm and then ﬁnd the

root (d

∗

). From this values, we can obtain p −1

and then the factorization of N.

To conclude the proof, we need to show that ev-

ery step of the method can be done in time polyno-

mial in log(N). The LLL-algorithm is polynomial in

the dimension of the matrix, that is O(m

), and in the

bit-size of its entries, that are O(mlogN). Addition-

ally, res

( f

, f

) has constant degree and coefﬁcients

bounded by a polynomial in N. Thus, every step can

be done in polynomial time.

5.2 Partial Information on MSB of d

∗

In this section, we prove that if the attacker knows a

sufﬁciently large number of most signiﬁcant bits of

the protected exponent d

∗

, then she can factor N.

To prove this result, we show how the partial

knowledge on d

∗

can be used to construct an approx-

imation of a multiple of p that allows to apply Theo-

rem 3.

Theorem 7. Let (N,e) be an RSA public key with e =

. Let d

= d mod p−1 and let d

∗

= d

+ ℓ(p−1),

for some ℓ = N

with σ ≥ 0. Suppose that N

α+σ

≤

and that we are given an approximation

∗

of d

∗

such that

∗

−

∗

| ≤ N

−α

Then, we can ﬁnd the factorization of N in time poly-

nomial in logN.

Proof. We start from equation

∗

−1 = k

∗

(p−1)

with k

∗

= k

+ ℓe.

Note that k

∗

≤ 2N

α+σ

implies that q can’t di-

vide k

∗

We compute an approximation

∗

p := e

∗

−1

of k

∗

p, up to an additive error of at most

∗

p−

∗

p| = |ed

∗

−1 + k

∗

−e

∗

+ 1|

= |e(d

∗

−

∗

) + k| ≤ N

+ 2N

α+σ

≤ 2N

Since the approximation

∗

p satisﬁes the hypothesis

of Theorem 3, we can ﬁnd the factorization of N in

time polynomial in logN.

The bound of Theorem 7 implies that an attacker

has to know at least log

M bits, where

M =

∗

−

∗

1+σ

−α

= 2N

+α+σ

(5)

This bound holds when the condition N

α+σ

≤

holds, which is not always the case in our settings. For

example an RSA modulus of 1024 bit with log

e =

256 and log

ℓ = 128 will have N

α+σ

≤ 2N

. For

these cases we are unaware of successful applications

of Coppersmith’s method.

In (Lu et al., 2014) Section 4 it is presented a novel

technique for the CRT case with better bound but with

the requirement to have d

not full size. This require-

ment also implies that no countermeasure is applied.

6 EXPERIMENTAL RESULTS

Here we present experimental results for the attacks

described in previous sections.

We consider RSA applications with 2048-bit mod-

ulus N and public exponent e = 2

+ 1, since this is

the most common choice made for real implementa-

tions.

In addition we assume that a random multiple ℓ

of φ(N) (or of (p−1) for CRT-RSA applications) is

added to the private exponent d (respectively d

For each dimension of ℓ, we ﬁrst report the theo-

retical bound on the minimum number of bits of the

secret key that the attacker needs to know to recover

NewResultsforPartialKeyExposureonRSAwithExponentBlinding

143

it entirely. This values are derived from theorems we

have proved in previous sections.

Then, we report the average minimum number of

bits that we really needed in our tests. In fact, theo-

retical bounds are reached when the lattice dimension

goes to inﬁnity. In general, the smaller is the number

of known bits, the bigger the lattice shall be. To con-

cretely mount an attack, one needs to construct a lat-

tice whose dimension is such that the LLL-algorithm

runs in practical time. Recall that the running time of

LLL-algorithm depends on the lattice dimension and

on the dimension of the entries of its matrix-basis.

Since the dimension of the entries depends on the

bounds X

and on the modular polynomial used, the

LLL-algorithm may have different running times for

the same lattice dimension.

We decided to ﬁx an upper bound on the dimen-

sion of the lattices we constructed. We chose the

threshold 80 as a tradeoff between efﬁciency and ef-

fectiveness of our attacks. Indeed, this choice allows

us to get closer to the theoretical bounds as opposed

to smaller dimensions. On the other hand, 80 is small

enough to make the LLL-algorithm running in practi-

cal time.

We ﬁxed the same threshold for all attacks in order

to compare their effectiveness when using the same

lattice dimension.

We implemented our methods with the SAGE

computer-algebra system (Stein et al., 2014) and run

it on a 3GHz Intel Core i5.

With the exception of the CRT-MSB case, where

we used only 10 experiments, for all other attacks

we ran 100 experiments generating different key pairs

and different values of ℓ. We report the average values

obtained from these experiments.

6.1 Results with known LSB of d

∗

In Section 4.1 we proved that if the attacker knows

a sufﬁciently large number of least signiﬁcant bits of

∗

, then she can factor N.

For generating the lattices, we used m = 11 and

t = τm, where τ is deﬁned in the proof of Theorem 4.

Notice that τ is always very small resulting in t = 0 for

each experiment. Thus, the dimension of the lattice is

ﬁxed and equal to 78.

In Table 1 we present our results. For different di-

mensions of ℓ we report theoretical and experimental

bounds on the minimum number of leaked bits neces-

sary to mount the attack. Then we report the lattice

dimension that allowed us to get the corresponding

experimental bound and ﬁnally the running time of

LLL-algorithm for these lattices.

The difference between theoretical and experi-

Table 1: Experimental results for partial key exposure attack

given least signiﬁcant bits of the secret exponent d

∗

= d +

ℓφ(N). The modulus N is 2048-bit long and e = 2

+ 1.

log

ℓ

theo.

bound

exp.

bound

dim(L) LLL

0 1040 1043 78 18 s

10 1060 1063 78 19 s

32 1103 1106 78 22 s

64 1164 1171 78 50 s

100 1232 1243 78 70 s

mental bounds is of very few bits and the LLL-

algorithm’s running time is really small.

It is worth to say that for ℓ = 0 and small e, the at-

tack in (Boneh et al., 1998) is more effective than our

attack. Indeed the n/4 least signiﬁcant bits of d are

sufﬁcient to factor N. However their attack requires

a brute-force search on k, that is allowed only when

e+ eℓ is small. Thus, for e = 2

+ 1 and ℓ = 0 their

method is more effective than ours. But, with the in-

troduction of exponent blinding, or for larger dimen-

sion of e, their method can’t be applied, because the

brute force-search becomes impractical.

Now, we compare our approach and the approach

of (Joye and Lepoint, 2012) for the same scenario.

We use a bivariate polynomial instead of a trivari-

ate polynomial, thus we perform a single resultant

computation, instead of three.

In order to compare the two approaches, we re-

port experimental results obtained using the same pa-

rameter choices made by the authors in (Joye and

Lepoint, 2012). Speciﬁcally, we consider 1000-bit

modulus N, public exponent e = 2

+ 1 and ℓ ∈

{10,100, 200, 300}.

As shown in Table 2, the theoretical bound is the

same, but our approach allows us to get closer to it.

Moreover, we do it by using smaller lattices.

6.2 Results with known MSB of d

∗

In this section we report experimental results on fac-

toring with knowledge of the most signiﬁcant bits of

the protected private exponent.

Since this method uses an univariate polynomial,

it is possible, in theory, to match the theoretical

limit, although the lattice dimension would make LLL

highly impractical. By imposing the threshold for

the maximum dimension of the lattice equal to 80,

the LLL-algorithm’s running time is about 2 hours.

For constructing such a lattice, we used m = 40 and

t = 40.

In Table 3 we present our results. We report the-

oretical and experimental bounds on the number of

SECRYPT2015-InternationalConferenceonSecurityandCryptography

144

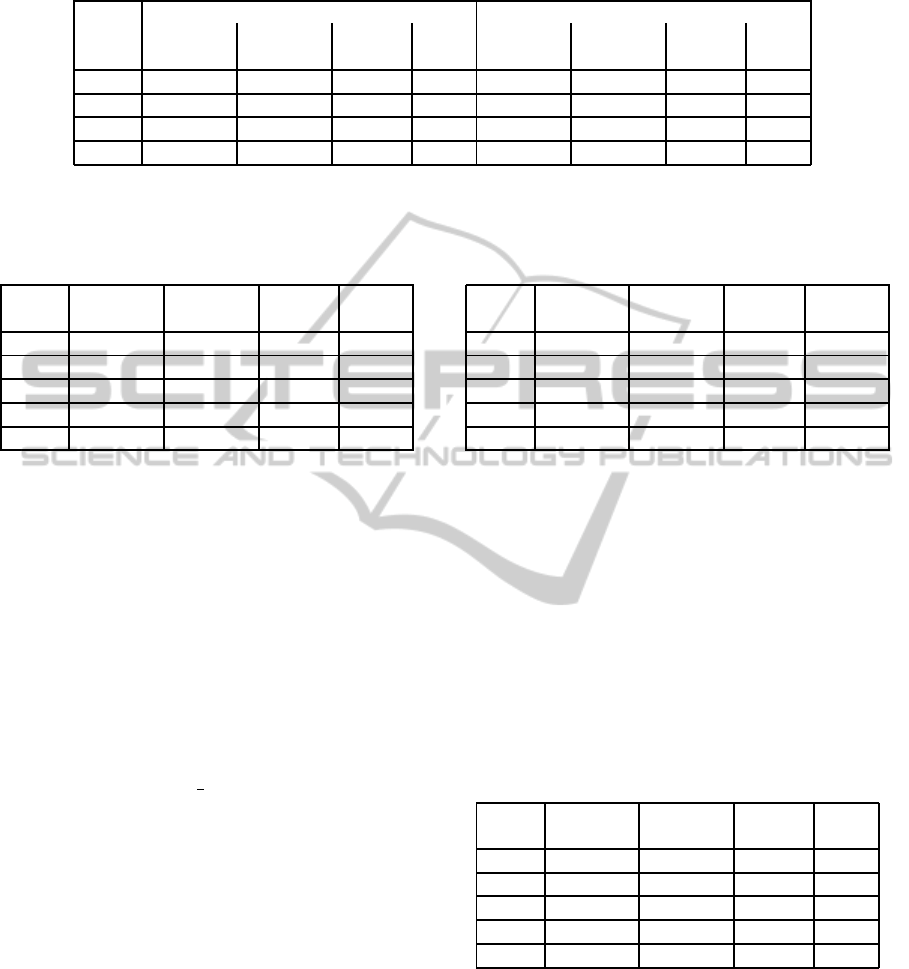
Table 2: Comparison between the approach of (Joye and Lepoint, 2012) and our approach for partial key exposure attack

given least signiﬁcant bits of the secret exponent d

∗

= d + ℓφ(N). The modulus N is 1000-bit long and e = 2

+ 1.

log

ℓ

Approach of (Joye and Lepoint, 2012) Our approach

theo.

bound

exp.

bound

dim(L) LLL

theo.

bound

exp.

bound

dim(L) LLL

10 535 580 16 1 sec 535 540 10 1 sec

100 700 760 16 1 sec 700 720 10 1 sec

200 871 960 16 1 sec 871 920 10 1 sec

300 1033 1160 16 1 sec 1033 1120 10 1 sec

Table 3: Experimental results for partial key exposure attack

given most signiﬁcant bits of the secret exponent d

∗

= d +

ℓφ(N). The modulus N is 2048-bit long and e = 2

+ 1.

log

ℓ

theo.

bound

exp.

bound

dim(L) LLL

0 1555 1555 80 112 m

10 1538 1555 80 112 m

32 1538 1555 80 112 m

64 1538 1555 80 112 m

100 1538 1555 80 112 m

leaked bits, the dimension of the lattice and the run-

ning time of the LLL-algorithm.

The experiments conﬁrmed the independence of

the boundwith respect to the dimension of the random

integer ℓ.

Unfortunately, in this case we cannot compare our

approach with the approach of (Joye and Lepoint,

2012), because they didn’t provide any experimen-

tal result respecting our assumptions. In fact, they

use very large values of ℓ, namely 500, 600 or 700-

bit long for a modulus N of size 1000 bits. These

unrealistic settings do not satisfy our requirement of

Lemma 1 for N

α+σ

≤2N

. In any case, our approach

improves their bound, as said in section 4.2.

Results using both MSB and LSB. As said in sec-

tion 4.2, it is possible to mount an attack knowing

both MSB and LSB of d

∗

. An univariate polynomial

is constructed and its root is found by constructing a

lattice as in the proof of Theorem 3. In Table 4 we

provide some experimental results for this method.

6.3 Results with known LSB of d

∗

In this section we report experimental results for CRT-

RSA applications when the attacker knows the least

signiﬁcant bits of the blinded private exponent d

∗

+ ℓ(p−1).

To get close to the theoretical bound, the lattice

dimension has to be signiﬁcantly increased. But this

Table 4: Experimental results for partial key exposure attack

given most and least signiﬁcant bits of the secret d

∗

= d +

ℓφ(N). The modulus N is 2048-bit long and e = 2

+ 1.

log

ℓ

theo.

bound

exp.

bound

dim(L) LLL

0 17+514 17+526 80 2h 27m

10 27+514 27+526 80 2h 27m

32 49+514 49+526 80 2h 27m

64 81+514 81+526 80 2h 27m

100 117+514 117+526 80 2h 27m

makes the LLL-algorithm’s running time highly im-

practical. By setting the threshold 80 for the lattice

dimension, the LLL-algorithm’s running time is about

13 minutes.

In Table 5 we present our results. We report the-

oretical and experimental bounds on the number of

leaked bits, the dimension of the lattice and the run-

ning time of the LLL-algorithm.

Table 5: Experimental results for partial key exposure attack

against CRT-RSA, given least signiﬁcant bits of the secret

exponent d

∗

= d

+ ℓ(p−1). The modulus N is 2048-bit

long and e = 2

+ 1.

log

ℓ

theo.

bound

exp.

bound

dim(L) LLL

0 617 691 78 8 m

10 637 712 78 10 m

32 681 758 78 13 m

64 745 822 78 17 m

100 817 894 78 18 m

In this case, the difference between theoretical and

experimental bounds is about 80 bits. Given a smaller

number of leaked bits one can still mount the attack by

constructing bigger lattices, but the computation will

need more time to end. For example, by setting t = 5

and m = 18 it is sufﬁcient to obtain 50 bits more than

the theoretical bound to solve. But the correspond-

ing lattice dimension is 190, which makes the LLL-

algorithm end in about one day. By setting t = 7 and

NewResultsforPartialKeyExposureonRSAwithExponentBlinding

145

m = 24 it is sufﬁcient to obtain 40 bits more than the

theoretical bound to solve. But the lattice dimension

is around 500 and we think that the LLL-algorithm

would be highly impractical in this case.

Notice that for ℓ = 0 and small e, Bl¨omer and May

show that a quarter of d

is sufﬁcient to the attacker

to factor N (Bl¨omer and May, 2003). To prove their

result, they use a brute-force search on k

, that is al-

lowed only when e+eℓ is small. Thus, for e = 2

and ℓ = 0 their method is better than our method, since

a smaller number of leaked bits are sufﬁcient to fac-

tor N. But, for larger dimension of e and when ℓ > 0

their method is no more effective because the brute

force-search becomes unfeasible.

6.4 Results with known MSB of d

∗

Here we report experimental results for CRT-RSA ap-

plications when the attacker knows the most signiﬁ-

cant bits of the protected private exponent.

Also in this case we imposed the threshold 80 for

the lattice dimension, which allowed us to run the

LLL-algorithm in practical time. We constructed lat-

tices by using m = 40 and t = 40.

In Table 6 we report the theoretical and experi-

mental number of leaked bits, the lattice dimension

and the running time of LLL-algorithm.

Table 6: Experimental results for partial key exposure attack

given most signiﬁcant bits of the CRT secret exponent d

∗

d + ℓ(p−1).

log

ℓ

theo.

bound

exp.

bound

dim(L) LLL

0 528 540 80 3h 03m

10 537 550 80 3h 59m

32 560 573 80 4h 23m

64 591 604 80 4h 52m

100 628 640 80 6h 13m

As opposite to the case based on LSB, this method

is the most effective also for ℓ = 0. Indeed, our

method is a generalization of (Bl¨omer and May,

2003), thus for ℓ = 0 we obtain their original result

which is the most effective method in literature for

this scenario.

7 CONCLUSIONS

We presented some methods to mount partial key ex-

posure attacks on RSA with exponent blinding. We

investigated both RSA and CRT-RSA, focusing on

practical settings for the exponents and the blinding

factor ℓ. In particular, we focused on public exponent

e such that 3 ≤ e < 2

256

, combining the upper bound

provided by NIST with the frequent value of 3. Addi-

tionally, we focused on full size private exponents and

ℓ < 2

128

, as commonly used in real implementations.

We derived sufﬁcient conditions to successfully

mount partial key exposure attacks in different sce-

narios and validated them providing numerical exper-

iments, using N of size 2048 and e = 2

+ 1, which

is the most commonly used setting in real implemen-

tations.

As for RSA, we improved the results of (Joye and

Lepoint, 2012) with the aim of reducing the number

of bits to be recovered by the adversary through side-

channel. In particular, when least signiﬁcant bits are

exposed, our approach allows to get closer to the the-

oretical bound by using smaller lattices, as shown in

Table 2. Whereas, when most signiﬁcant bits are ex-

posed, we presented a method that does not rely on the

heuristic assumption and that provides better bounds,

as shown in Section 4.2.

Additionally, we provided novel results for the

particular case where the adversary is able to recover

non-consecutive portions of the private information.

As for CRT-RSA with exponent blinding, we pro-

vided novel results for both scenarios when either

least or most signiﬁcant bits are exposed.

In Table 7, we recap the numerical results we ob-

tained from our experiments. For each dimension of

ℓ we provide the minimum number of bits of the pro-

tected exponent that is sufﬁcient to the attacker to suc-

cessfully break the system.

With the only exception of the RSA attack based

on most signiﬁcant bits, the number of known bits de-

pends on the bit-size of the blinding factor ℓ.

ACKNOWLEDGEMENTS

This work was partly supported by the Italian MIUR

project SecurityHorizons (c.n. 2010XSEMLC).

REFERENCES

Bl¨omer, J. and May, A. (2003). Newpartial key exposure at-

tacks on RSA. In Boneh, D., editor, Advances in Cryp-

tology - CRYPTO 2003, Proceedings, volume 2729 of

LNCS, pages 27–43. Springer.

Boneh, D., Durfee, G., and Frankel, Y. (1998). An attack

on RSA given a small fraction of the private key bits.

In Ohta, K. and Pei, D., editors, Advances in Cryptol-

ogy - ASIACRYPT 1998, Proceedings, volume 1514 of

LNCS, pages 25–34. Springer.

SECRYPT2015-InternationalConferenceonSecurityandCryptography

146

Table 7: The number of bits that the attacker needs to know to successfully mount partial key exposure attacks. The modulus

N is 2048-bit long and the public exponent is e = 2

+ 1. The private exponent is blinded using the random factor ℓ.

log

ℓ LSB MSB MSB+LSB CRT-LSB CRT-MSB

0 1043 1555 17+526 691 540

10 1063 1555 27+526 712 550

32 1106 1555 49+526 758 573

64 1171 1555 81+526 822 604

100 1243 1555 117+526 894 640

Clavier, C., Feix, B., Gagnerot, G., Roussellet, M., and

Verneuil, V. (2010). Horizontal correlation analysis on

exponentiation. In Soriano, M., Qing, S., and L´opez,

J., editors, Information and Communications Security

- ICICS 2010, Proceedings, volume 6476 of LNCS,

pages 46–61. Springer.

Coppersmith, D. (1996a). Finding a small root of a bivariate

integer equation; factoring with high bits known. In

(Maurer, 1996), pages 178–189.

Coppersmith, D. (1996b). Finding a small root of a uni-

variate modular equation. In (Maurer, 1996), pages

155–165.

Coron, J. (1999). Resistance against differential power anal-

ysis for elliptic curve cryptosystems. In Koc¸, C¸. K. and

Paar, C., editors, Cryptographic Hardware and Em-

bedded Systems - CHES 1999, Proceedings, volume

1717 of LNCS, pages 292–302. Springer.

Ernst, M., Jochemsz, E., May, A., and de Weger, B. (2005).

Partial key exposure attacks on RSA up to full size ex-

ponents. In Cramer, R., editor, Advances in Cryptol-

ogy - EUROCRYPT 2005, Proceedings, volume 3494

of LNCS, pages 371–386. Springer.

Fouque, P., Kunz-Jacques, S., Martinet, G., Muller, F., and

Valette, F. (2006). Power attack on small RSA pub-

lic exponent. In Goubin, L. and Matsui, M., editors,

Cryptographic Hardware and Embedded Systems -

CHES 2006, Proceedings, volume 4249 of LNCS,

pages 339–353. Springer.

Herrmann, M. and May, A. (2008). Solving linear equa-

tions modulo divisors: On factoring given any bits.

In Pieprzyk, J., editor, Advances in Cryptology - ASI-

ACRYPT 2008, Proceedings, volume 5350 of LNCS,

pages 406–424. Springer.

Howgrave-Graham, N. (1997). Finding small roots of uni-

variate modular equations revisited. In Darnell, M.,

editor, Cryptography and Coding, 6th IMA Interna-

tional Conference 1997, Proceedings, volume 1355 of

LNCS, pages 131–142. Springer.

Joye, M. and Lepoint, T. (2012). Partial key exposure on

RSA with private exponents larger than N. In Ryan,

M. D., Smyth, B., and Wang, G., editors, Informa-

tion Security Practice and Experience - ISPEC 2012,

Proceedings, volume 7232 of LNCS, pages 369–380.

Springer.

Kerry, C. F., Secretary, A., and Director, C. R. (2013). FIPS

PUB 186-4 FEDERAL INFORMATION PROCESS-

ING STANDARDS PUBLICATION Digital Signa-

ture Standard (DSS).

Kocher, P. C. (1996). Timing attacks on implementations of

difﬁe-hellman, rsa, dss, and other systems. In Koblitz,

N., editor, Advances in Cryptology - CRYPTO 1996,

Proceedings, volume 1109 of LNCS, pages 104–113.

Springer.

Kocher, P. C., Jaffe, J., and Jun, B. (1999). Differential

power analysis. In Wiener, M. J., editor, Advances

in Cryptology - CRYPTO 1999, Proceedings, volume

1666 of LNCS, pages 388–397. Springer.

Lenstra, A., Lenstra, H., and Lov´asz, L. (1982). Factoring

polynomials with rational coefﬁcients. Math. Ann.,

261:515–534.

Lu, Y., Zhang, R., and Lin, D. (2014). New partial key

exposure attacks on CRT-RSA with large public ex-

ponents. In Boureanu, I., Owesarski, P., and Vaude-

nay, S., editors, Applied Cryptography and Network

Security - ACNS 2014, Proceedings, volume 8479 of

LNCS, pages 151–162. Springer.

Maurer, U. M., editor (1996). Advances in Cryptology - EU-

ROCRYPT 1996, Proceeding, volume 1070 of LNCS.

Springer.

May, A. (2003). New RSA vulnerabilities using lattice re-

duction methods. PhD thesis, University of Paderborn.

Quisquater, J.-J. and Couvreur, C. (1982). Fast decipher-

ment algorithm for rsa public-key cryptosystem. Elec-

tronic Letters, 18:905–907.

Stein, W. et al. (2014). Sage Mathematics Soft-

ware (Version 6.2). The Sage Development Team.

http://www.sagemath.org

Walter, C. D. (2001). Sliding windows succumbs to big

mac attack. In Koc¸, C¸ . K., Naccache, D., and Paar,

C., editors, Cryptographic Hardware and Embedded

Systems - CHES 2001, Proceedings, volume 2162 of

LNCS, pages 286–299. Springer.

Wiener, M. J. (1990). Cryptanalysis of short rsa secret ex-

ponents. IEEE Transactions on Information Theory,

36:553–558.

NewResultsforPartialKeyExposureonRSAwithExponentBlinding

147