Temporal-Difference Learning
An Online Support Vector Regression Approach
Hugo Tanzarella Teixeira and Celso Pascoli Bottura
State University of Campinas - UNICAMP, School of Electrical and Computer Engineering - FEEC, DSIF-LCSI,
Av. Albert Einstein, N. 400 - LE31 - CEP 13081-970, Campinas, SP, Brazil
Keywords:
Machine Learning, Reinforcement Learning, Temporal Difference Learning, Value Function Approximation,
Online Support Vector Machine.
Abstract:
This paper proposes a new algorithm for Temporal-Difference (TD) learning using online support vector re-
gression. It benefits from the good generalization properties support vector regression (SVR) has, and also
can do incremental learning and automatically track variation of environment with time-varying characteris-
tics. Using the online SVR we can obtain good estimation of value function in TD learning in linear and
nonlinear prediction problems. Experimental results demonstrate the effectiveness of the proposed method by
comparison with others methods.
1 INTRODUCTION
Reinforcement learning (RL) problems are closely re-
lated to optimal control problems, particularly formu-
lated as a Markov decision process (MDP) (Sutton
and Barto, 1998). RL methods are based on a math-
ematical technique known as dynamic programming
(DP), first introduced by Bellman (Bellman, 1957).
In recent years, RL has been widely studied not only
in the machine learning and neural network com-
munities but also in control theory (Lewis and Vra-
bie, 2009; Wang et al., 2009; Bus¸oniu et al., 2010;
Szepesv´ari, 2010; Powell, 2011).
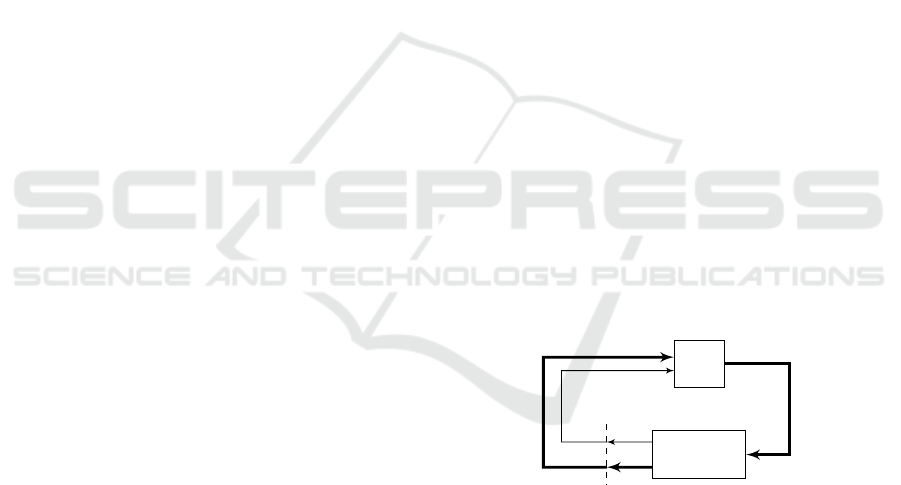
In RL paradigm, an agent (controler) must learn
from interaction with its environment (plant), see Fig-
ure 1. The goal of the RL agent is to estimate the
optmal policy or optimal value function for MDP.
Temporal-difference (TD) learning is a popular
family of algorithms for approximate policy evalu-
ation for MDPs. Introduced in (Sutton, 1988), is a
method for approximating long-term future cost as a
function of current state. The algorithm is recursive,
efficient, and simple to implement (Tsitsiklis and Roy,
1997). For small Markov chains, computing estimates
of value function is a trivial task easily realized with
traditional tabular TD. However,in many practical ap-
plications a RL agent has to deal with MDPs with
large or continuous state spaces. In such case the tab-
ular TD algorithm suffer from the curse of dimension-
ality (Powell, 2011).
Agent
Environment
action
u
t
r
t+1
reward
r
t
x
t+1
state
x
t
Figure 1: Agent-environment interaction (Sutton and Barto,
1998).
A possible approach to deal with this curse is to
approximate the value function (Bertsekas and Tsit-
siklis, 1996). There are several value function approx-
imation (VFA) techniques, such as linear function ap-
proximation (Boyan, 2002), neural networks (Liu and
Zhang, 2005), and kernel methods (Xu, 2006).
The generalization property is an important factor
to determine the prediction performance of function
approximation. The support vector machine (SVM)
is known to have good properties over the general-
ization (Sch¨olkopf and Smola, 2001).Support vector
regression (SVR), originally introduced in (Drucker
et al., 1997), is an extension of the SVM algorithm for
classification to the problem of regression. However,
SVR does not lend itself readily to recursive updat-
ing, so it has not been suitable for problems where the
target values of existing observations change quickly,
e.g. RL (Powell, 2011; Martin, 2002). To deal with
this limitation, (Martin, 2002) and (Ma et al., 2003)
developed, apparently independently, an online sup-
318
Tanzarella Teixeira H. and Pascoli Bottura C..
Temporal-Difference Learning - An Online Support Vector Regression Approach.
DOI: 10.5220/0005572103180323
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 318-323
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
port vector regression (OSVR) algorithm.
In this paper, OSVR is used to directly approx-
imate state value function in TD methods. Our ap-
proach applies, at each step, the TD error to improve
the OSVR value function approximation.
Introductions to TD learning and OSVR are sum-
marized in Section 2 and Section 3, respectively. Sec-
tion 4 presents the OSVR TD algorithm, and in Sec-
tion 5, some experimental results on typical value-
function learning predictions of a Markov chain are
shown to evaluate the performance of the proposed
method. Section 6 draws conclusions.
2 TEMPORAL-DIFFERENCE
LEARNING
TD learning is a combination of Monte Carlo and DP
ideas. TD methods can learn directly from raw experi-
ence without a model of the environment’s dynamics
and update estimates based in part on other learned
estimates, without waiting for a final outcome (Sutton
and Barto, 1998).
We address the problem of estimating the value
function V
π
of a state x under a given police π in MDP
(policy evaluation or prediction problem), which is
defined as
V
π
(x) = E
π
"
∞
∑
k=0
γ
k
r
t+k+1
x
t
= x
#
(1)
where x is an initial state, r is a reward, and E
π
[·] de-
notes the expected value given that the agent follows
policy π. This is an important sub-problem of several
algorithms for the control problem (finding an opti-
mal policy) (Sutton and Barto, 1998), such as fitted-Q
iteration, approximate policy iteration, and adaptive
critic design (ACD) (Xu et al., 2014).
The TD method uses experience to solve the pre-
diction problem; given some experience following a
policy π they estimate an approximate value function
V of V
π
. If a nonterminal state x
t
is visited at time t,
TD methods need to wait until the next time step to
update their estimate V(x
t
). At time t + 1 they imme-
diately form a target and make an useful update using
the observed reward r
t+1
and the estimate V(x
t+1
). The
simplest TD method, known as TD(0), is
V(x
t
) ← V(x
t
) + α[r
t+1
+ γV(x
t+1
) −V(x
t
)] (2)
where α is a constant step-size parameter and 0 ≤ γ ≤ 1
is a discount rate, and the TD error is defined as
δ
t
= r
t+1
+ γV(x
t+1
) −V(x
t
) (3)
3 ONLINE SUPPORT VECTOR
REGRESSION
The key idea of the OSVR algorithm consists of up-
dating a SVR model to meet the Karush-Kuhn-Tucker
(KKT) conditions that the SVR model must fulfill
when training data are added or deleted.
The following subsection provides a basic
overview of SVR; for more details, see (Smola and
Sch¨olkopf, 2004).
3.1 Support Vector Regression Basics
The objective of the SVR problem is to learn a func-
tion
f(x) = w
T
ϕ(x) + b (4)
that gives a good approximationof a given set of train-
ing data {x
i
,y
i
}
n
i=1
where x
i
∈ R
m
is the input and y
i
∈ R
is the observed output, {ϕ
j
(x)}
m
b
j=1
is a set of nonlinear
basis functions that maps an input space into a feature
space, the parameter vector w ∈ R
m
b
and the bias b are
unknown. The problem is to compute estimates of w
which minimizes the norm ||w||
2
= w
T
w. We can write
this problem as a convex optimization problem:
minimize:
1
2
w
T
w
subject to: y
i
− w
T
ϕ(x
i
) − b ≤ ε
w
T
ϕ(x
i
) + b− y
i
≤ ε
i = 1,2,. . . ,n
(5)
The support vector (SV) method was first de-
veloped for pattern recognition (Cortes and Vapnik,
1995). To generalize the SV algorithm to the regres-
sion case, an analog of the soft margin is constructed
in the space of the observed output y by using Vap-
nik’s ε-insensitive loss function (Vapnik, 1995) de-
scribed by
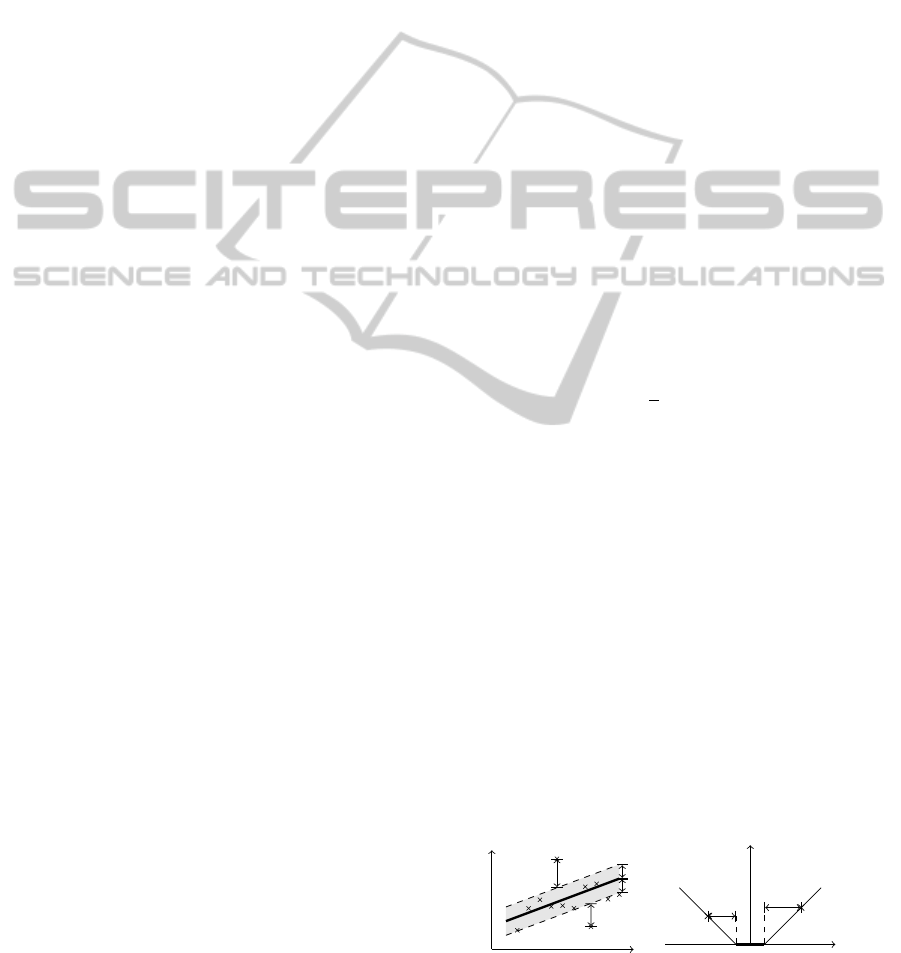
c(x,y, f(x)) := max{0,|y− f(x)| − ε} (6)
Figure 2 depicts this situation graphically for a uni-
dimensional case. Only the points outside the shaded
region contribute to the cost insofar, as the deviations
are penalized in a linear fashion.
x
y
×
×
×
×
×
×
×
×
×
×
×
ξ
×
ξ
′
+ε
0
−ε
(a) A ε-tube fitted to
data.
y−g(x, w)
0
c
ε
(y, f (x,w))
−ε
+ε
×
ξ
×
ξ
′
(b) Linear ε-insensitive
loss function.
Figure 2: The soft margin loss setting for a linear SVR.
Temporal-DifferenceLearning-AnOnlineSupportVectorRegressionApproach
319

Now, we can transform the optimization problem
(5) by introducing slack variables, denoted by ξ
i
, ξ
′
i
:
minimize:
1
2
w
T
w+C
n
∑
i=1
(ξ
i
+ ξ
′
i
)
subject to: y
i
− w
T
ϕ(x
i
) − b ≤ ε + ξ
i
w
T
ϕ(x
i
) + b− y
i
≤ ε+ ξ
′
i
ξ
i
,ξ
′
i
≥ 0
i = 1,2,. ..,n
(7)
where, the regularization term
1
2
w
T
w penalizes model
complexity, and C is a non-negative weight which de-
termines how much prediction errors which exceed
the threshold value ε are penalized.
The minimization problem (7) is difficult to solve
when the number n is large. To address these issue,
one can solve the primal problem through its dual,
which can be formulated finding a saddle point of the
associated Lagrange function (Vapnik, 1995)
L(w,ξ,ξ
′
,α,α
′
,β,β
′
)
=
1
2
||w||
2
+C
n
∑
i=0
(ξ
i
+ ξ
′
i
) −
n
∑
i=1
(β
i
ξ
i
+ β
′
ξ
′
i
)
+
n
∑
i=1
α
i
(y
i
− w
T
ϕ(x
i
) − ε − ξ
i
)
+
n
∑
i=1
α
′
i
(w
T
ϕ(x
i
) − y
i
− ε− ξ
i
) (8)
which is minimized with respect to w, ξ
i
and ξ
′
i
and
maximized with respect to Lagrange multipliers α
i
,
α
′
i
,β
i
,β
′
i
≥ 0. It fallows from the saddle point condi-
tion that the partial derivatives of L with respect to the
primal variables (w
i
,w
0
,ξ
i
,ξ
′
i
) have to vanish for opti-
mality.
∂
w
L = w−
n
∑
i=1
(α
i
− α
′
i
)x
i
= 0, (9)
∂
b
L =
n
∑
i=1
(α
i
− α
′
i
) = 0 (10)
∂
ξ
i
L = C − α
i
− β
i
= 0, (11)
∂
ξ
′
i
L = C − α
′
i
− β
′
i
= 0, (12)
i = 1,2,. . . ,n
Substituting (9)–(12) into (8) yields the dual opti-
mization problem.
maximize: −
1
2
n
∑
i, j=1
(α
i
− α
′
i
)(α
j
− α
′
j
)ϕ(x
i
)
T
ϕ(x
j
)
+
n
∑
i=1
(α
i
− α
′
i
)y
i
− ε
n
∑
i=1
(α
i
+ α
′
i
)
subject to:
n
∑
i=1
(α
i
− α
′
i
) = 0
0 ≤ α
i
,α
′
i
≤ C
i = 1,2,. .. ,n
(13)
In deriving (13) we already eliminated the dual vari-
ables β
i
, β
′
i
through conditions (11) and (12). Equa-
tion (9) can be rewritten as follows
w =
n
∑
i=1
(α
i
− α
′
i
)ϕ(x
i
) (14)
The corresponding KKT complementarity conditions
are
α
i
(y
i
− w
T
ϕ(x
i
) − b− ε− ξ
i
) = 0 (15)
α
′
i
(w
T
ϕ(x
i
) + b− y
i
− ε− ξ
i
) = 0 (16)
ξ
i
ξ
′
i
= 0,α
i
α
′
i
= 0 (17)
(α
i
−C)ξ
i
= 0,(α
′
i
−C)ξ
′
i
= 0 (18)
i = 1,2,. . . ,n
From (15) and (16) it follows that the Lagrange mul-
tipliers may be nonzero only for |y
i
− g(x
i
)| ≥ ε; i.e.,
for all samples inside the ε-tube (the shaded region in
Figure 2(a)) the α
i
,α
′
i
vanish. This is because when
|y
i
− g(x
i
)| < ε the second factor in (15) and (16) is
nonzero, hence α
i
,α
′
i
must be zero for the KKT con-
ditions to be satisfied. Therefore we have a sparse
expansion of w in terms of x
i
(we do not need all x
i
to describe w). The samples that come with nonva-
nishing coefficients are called support vectors. Thus
substituting (14) into (4) yields the so-called support
vector expansion
f(x) =
n
sv
∑
i=1
(α
i
− α
′
i
)ϕ(x
i
)
T
ϕ(x) + b (19)
where n
sv
is the number of support vectors. Now, a
final note must be made regarding the basis function
vector ϕ(x). In (13) and (19) it appears only as inner
products. This is important, because in many cases a
kernel function K(x
i
,x
j
) = ϕ(x
i
)
T
ϕ(x
j
) can be defined
whose evaluation avoids the need to explicitly calcu-
late the vector ϕ(x). This is possible only if the kernel
function satisfies the Mercer’s condition, for more de-
tails (Sch¨olkopf and Smola, 2001).
3.2 Online Support Vector Regression
Algorithm
The Lagrange formulation of (13) can be represented
as
L
D
(α,α
′
,δ,δ
′
,u,u
′
,ζ)
=
1
2
N
∑
i, j=1
(α
i
− α
′
i
)(α
j
− α
′
j
)k(x
i
,x
j
) −
N
∑
i=1
(α
i
− α
′
i
)y
i
+ ε
N
∑
i=1
(α
i
+ α
′
i
) −
N
∑
i=1
(δ
i
α
i
+ δ
′
i
α
′
i
)
+
N
∑
i=1
[η
i
(α
i
−C) + η
′
i
(α
′
i
−C)] + ζ
N
∑
i=1
(α
i
− α
′
i
) (20)
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
320

where δ
i
, δ
′
i
, η
i
,η
′
i
≥ 0 and ζ are the new Lagrange mul-
tipliers. Once again, the partial derivatives of L
D
with
respect to the primal variables (α
i
,α
′
i
) must vanish:
∂
α
i
L
D
= 0
N
∑
j=1
(α
j
− α
′
j
)k(x
i
,x
j
) − y
i
+ ε− δ
i
+ η
i
+ ζ = 0 (21)
∂
α
′
i
L
D
= 0
−
N
∑
j=1
(α
j
− α
′
j
)k(x
i
,x
j
) + y
i
+ ε− δ
′
i
+ η
′
i
− ζ = 0, (22)
i = 1,2,. ..,N
Note that ζ in (21) and (22) is equal to b in (4) and (19)
at optimality (Martin, 2002; Ma et al., 2003). The
corresponding KKT complementarity conditions are
δ
i
α
i
= 0, δ
′
i
α
′
i
= 0, (23)
η
i
(α
i
−C) = 0, η
′
i
(α
′
i
−C) = 0, (24)
i = 1,2,. ..,N
Since α
i
α
′
i
= 0 (Cristianini and Shawe-Taylor, 2000;
Sch¨olkopf and Smola, 2001), and α
i
,α
′
i
≥ 0, we can
define a coefficient difference θ
i
= α
i
− α
′
i
, and define
a margin function h(x
i
) as:
h(x
i
) := f (x
i
) − y
i
=
N
∑
j=1
θ
j
k(x
i
,x
j
) + b− y
i
(25)
Combining equations (21) to (25), the KKT condi-
tions can be rewritten as:
h(x
i
) > ε, θ
i
= −C
h(x
i
) = ε, −C < θ
i
< 0
−ε < h(x
i
) < ε, θ
i
= 0
h(x
i
) = −ε, 0 < θ
i
< C
h(x
i
) < −ε, θ
i
= C
(26)
Based in relations (26), each sample in training set
T can be classified in three different subsets:
Margin support vectors: S = {i| |θ
i
| = C}
Error support vectors: E = {i| 0 < |θ
i
| < C}
Remaining samples: R = {i| θ
i
= 0}
The geometric representation, in a unidimensional
case, of training set samples distribution into subsets
S, E and R can be viewed in Figure 3.
When a new data pair (x
c
,y
c
) is added to the train-
ing set T , the OSVR algorithm update the trained
SVR function. Each new training datum must sat-
isfy one of the conditions in (26). If (x
c
,y
c
) belongs
to R , there is no need to update the SVR model. On
the other hand, if (x
c
,y
c
) belongs to E or S , the initial
value of θ
c
is gradually changed to meet KKT condi-
tions (Ma et al., 2003). When one datum is deleted
from training data, the same iterative calculation is
performed until all remaining data in T satisfies the
KKT conditions. The complete description of OSVR
algorithm can be found in (Martin, 2002) and (Ma
et al., 2003).
0
x
h(x)
ε
−ε
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
× × ×
× ×
R , θ
i
= 0
E, θ
i
= −C
E, θ
i
= C
S, −C < θ
i
< 0
S, 0 < θ
i
< C
Figure 3: Decomposition of T into S, E e R following KKT
conditions.
4 OSVR TD ALGORITHM
In the OSVR TD algorithm the value functions in (2)
are approximated using a SV expansion (19):
ˆ
V(x) =
n
SV
∑
i=1
(α
i
− α
′
i
)k(x
x
i
,x
x
) (27)
and the parameters α
i
and α
′
i
are obtained using
the OSVR algorithm described in earlier an section.
Thus, the TD error is now given by
δ
t
= r
t+1
+ γ
ˆ
V(x
t+1
) −
ˆ
V(x
t
)
Therefore, the OSVR TD algorithm runs the fol-
lowing iteration steps:
1. The OSVR model
ˆ
V (27), for a policy π to be eval-
uated, is initialized with no data in T set.
2. Repeat for each episode:
(a) The state x is initialized as the initial state of the
episode
(b) Repeat for each episode step, until x is a termi-
nal state
i. For an action u given by π for x, observe re-
ward r, and next state x
′
ii. Compute the TD error:
δ
t
= r+ γ
ˆ
V(x
′
) −
ˆ
V(x
′
)
iii. Update the approximated value function for
state x:
¯
V(x) =
ˆ
V(x) + αδ
iv. If is the first time which state x was visited,
the pair (x,
¯
V) is added in training set T , and
the OSVR model
ˆ
V is updated.
v. If the state x has been visited earlier. The
datum x has been removed from the OSVR
model
ˆ
V and the pair (x,
¯
V) is added in training
set T , then OSVR model
ˆ
V is updated.
In the next section, illustrative examples of value
function predictions for Markov chains are given to
show the effectiveness of the proposed OSVR-TD al-
gorithm.
Temporal-DifferenceLearning-AnOnlineSupportVectorRegressionApproach
321

5 EXPERIMENTAL RESULTS
The Hop-World problem, studied in (Boyan, 2002)
is a 13-state Markov chain with an absorbing state,
pictured in Figure 4. Each non-absorbing state has
two possible state transitions with transition probabil-
ity 0.5. In the linear case, the true value function for
state i is V
π
(i) = −2i, and in the nonlinear variation of
the Hop-World problem, the true value function for
state i is given by V
π
(i) = −i
2
.
In our simulation, the OSVR-TD algorithm is
compared to conventional linear TD(λ) (Boyan,
2002), LSTD(λ) and RLST(λ) (Xu et al., 2002). In
the experiments, an episode is defined as the period
from the random initial state to the terminal state 0.
The performances of the algorithms are evaluated by
the averaged root mean squared (RMS) error of value
function predictions over all the 13 states. The pa-
rameters set of each algorithm were chosen to achieve
the lowest possible RMS error, and are summarized in
Table 1. Further, the step-size parameter of TD(λ) has
the form α
n
= α
0
(n
0
+ 1)/(n
0
+ n), the RLSTD(λ) has
initial variance matrix P
0
= 500I, and forgetting factor
µ = 0.095. A radial basis function (RBF), with stan-
dard deviation σ = 0.67, was chosen as kernel func-
tion. The complexity term C is set to be 20 for the
linear Hop-World problem and it is set to be 100 for
the nonlinear case. For TD(λ), LSTD(λ) and RLST(λ)
algorithms, each state is represented by four features,
as follows: the representation for states 12, 8, 4 and
0 are, respectively, [1,0,0,0], [0,1,0,0], [0,0,1,0], and
[0,0,0,1]; and the representations for the other states
are obtained by linearly interpolating between these
(Boyan, 2002). For OSVR-TD algorithm no featur-
ization in state space is needed.
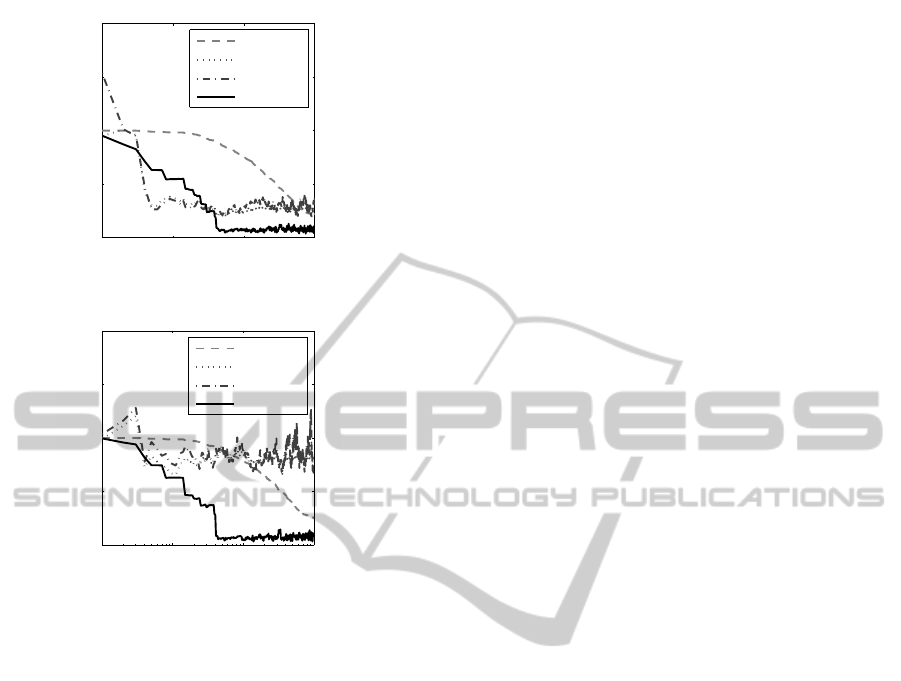
Table 2(a) show the RMS prediction of tested al-
gorithms at the end of 10,100 and 1000 episodes for
linear experiments, while Table 2(b) show the results
for the nonlinear case. In Figure 5 we can see the
learning curves of conventional linear TD(λ) (dashed
line), LSTD(λ) (dotted line), RLST(λ) (dotted dashed
line) and OSVR-TD (solid line). The RMS error
in these graphics are normalized with a RMS error
for initial VFA V = 0 for all states. In linear case,
Figure 5(a), although LSTD(λ) and RLST(λ) algo-
rithms convergeearlier than OSVR-TD algorithm, the
OSVR-TD algorithm had lower RMS error after con-
vergence. In nonlinear case, Figure 5(b), LSTD(λ)
and RLST(λ) algorithms could not have achieved sig-
nificant results predicting the value function.
0
12
...
10
1112
rrrrr
r
r
r
r
r
r
Figure 4: A 13-state Markov chain (Boyan, 2002).
Table 1: Algorithms parameters.
Algorithm γ λ α
(0)
n
0
TD(λ) 1.0 0.4 0.01 1000
LSTD(λ) 0.9 0.9 - -
RLSTD(λ) 0.9 0.3 - -
OSVR-TD 1.0 - 0.8 -
Table 2: Performance comparison between TD(λ),
LSTD(λ), RLSTD(λ) and OSVR-TD.
(a) Linear Hop-World
Algorithm
Episodes
10 100 100
TD(λ) 13.89 10.69 3.10
LSTD(λ) 5.40 3.36 3.87
RLSTD(λ) 5.11 3.87 5.16
OSVR-TD 7.73 0.99 1.06
(b) Nonlinear Hop-World
Algorithm
Episodes
10 100 100
TD(λ) 67.45 53.77 17.21
LSTD(λ) 46.12 57.47 55.33
RLSTD(λ) 52.64 60.22 47.67
OSVR-TD 43.04 3.80 4.61
6 CONCLUSION
This paper proposes a new method of VFA for TD
learning based on OSVR models. Compared to tra-
ditional algorithms TD(λ), LSTD(λ) and RLSTD(λ),
it has significant values for nonlinear approximation
abilities. The OSVR-TD has been applied success-
fully both to linear and nonlinear Hop-World prob-
lems. In addition to having achieved better results
than other algorithms, no featurization is necessary
in the state space, in spite of the necessary tuning of
the OSVR model parameters. More theoretical and
experimental analysis on the OSVR-TD algorithm as
well an extension to learning control problems is our
ongoing work.
ACKNOWLEDGEMENTS
The authors acknowledge CAPES for the support.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
322
10
0
10
1
10
2
10
3
0
0.5
1
1.5
2
Episodes
RMS error
Linear HopWorld
TD(λ)
LSTD(λ)
RLSTD(λ)
OSVR−TD
(a) Linear Hop-World
10
0
10
1
10
2
10
3
0
0.5
1
1.5
2
Episodes
RMS error
Nonlinear HopWorld
TD(λ)
LSTD(λ)
RLSTD(λ)
OSVR−TD
(b) Nonlinear Hop-World
Figure 5: Performance comparison between TD(λ),
LSTD(λ), RLSTD(λ) and OSVR-TD.
REFERENCES
Bellman, R. E. (1957). Dynamic programing. Princeton
University Press, Princeton, NJ.
Bertsekas, D. P. and Tsitsiklis, J. N. (1996). Neuro-Dynamic
Programming. Athena Scientific, Nashua, NH, 1st
edition.
Boyan, J. A. (2002). Technical update: Least-squares tem-
poral difference learning. Machine Learning, 49:233–
246.
Bus¸oniu, L., Babuˇska, R., Schutter, B. D., and Ernst,
D. (2010). Reinforcement Learning and Dynamic
Programming Using Function Approximators. CRC
Press, Inc., Boca Raton, FL, USA.
Cortes, C. and Vapnik, V. (1995). Support vector networks.
Machine Learning, 20:273–297.
Cristianini, N. and Shawe-Taylor, J. (2000). An Introduction
to Support Vector Machines: And Other Kernel-based
Learning Methods. Cambridge University Press, New
York, NY, USA.
Drucker, H., Burges, C. J. C., Kaufman, L., Smola, A.,
and Vapnik, V. (1997). Support vector regression ma-
chines. Advances in neural information processing
systems, (9):155–161.
Lewis, F. L. and Vrabie, D. (2009). Reinforcement learn-
ing and approximate dynamic programming for feed-
back control. IEEE Circuits and Systems Magazine,
9(3):32–50.
Liu, D. and Zhang, H. (2005). A neural dynamic program-
ming approach for learning control of failure avoid-
ance problems. Intelligent Control and Systems, In-
ternational Journal of, 10(1):21–32.
Ma, J., Theiler, J., and Perkins, S. (2003). Accurate on-
line support vector regression. Neural Computation,
15(11):2683–2704.
Martin, M. (2002). On-line suport vector machines for func-
tion approximation. Software Department, Universi-
tat Polit`ecnica de Catalunya, Technical Report(LSI-
02-11-R):1–11.
Powell, W. B. (2011). Approximate Dynamic Program-
ming: Solving the Curses of Dimensionality. Wiley,
Hoboken, 2nd edition.
Sch¨olkopf, B. and Smola, A. J. (2001). Learning with Ker-
nels: Support Vector Machines, Regularization, Opti-
mization, and Beyond. MIT Press, Cambridge, MA,
USA.
Smola, A. J. and Sch¨olkopf, B. (2004). A tutorial on
support vector regression. Statistics and Computing,
14(3):199–222.
Sutton, R. S. (1988). Learning to predict by the method of
temporal differences. Machine Learning, 3:9–44.
Sutton, R. S. and Barto, A. G. (1998). Reinforcement Learn-
ing, An Introduction. MIT Press, Cambridge, MA,
USA, 1st edition.
Szepesv´ari, C. (2010). Algorithms for Reinforcement
Learning. Morgan & Claypool Publishers, Alberta,
Canada.
Tsitsiklis, J. N. and Roy, B. V. (1997). An analysis of
temporal-difference learning with function approxi-
mation. IEEE Transactions on Automatic Control,
42(5):674–690.
Vapnik, V. N. (1995). The nature of statistical learning the-
ory. Springer-Verlag, New York.
Wang, F. Y., Zhang, H., and Liu, D. (2009). Adaptive dy-
namic programming: An introduction. IEEE Compu-
tational Intelligence Magazine, 4(2):39–47.
Xu, X. (2006). A sparse kernel-based least-squares tem-
poral difference algorithm for reinforcement learning.
Proceedings of the Second International Conference
on Advances in Natural Computation, Part I:47–56.
Xu, X., gen He, H., and Hu, D. (2002). Efficient reinforce-
ment learning using recursive least-squares methods.
Artificial Intelligence Research, Journal of, 16:259–
292.
Xu, X., Zuo, L., and Huang, Z. (2014). Reinforcement
learning algorithms with function approximation: Re-
cent advances and applications. Information Sciences,
261:1–31.
Temporal-DifferenceLearning-AnOnlineSupportVectorRegressionApproach
323
