
A Diagnosis Scheme for Dynamical Systems: Approach by Guaranteed
Parameter Estimation
Qiaochu Li
1
, Carine Jauberthie
2
, Lilianne Denis-Vidal
1
and Zohra Cherfi
1
1
Sorbonne University, Universit
´
e de Technologie de Compi
`
egne, 60 203 Compi
`
egne cedex, France
2
LAAS, CNRS, 7 avenue du Colonel Roche, France Universit
´
e de Toulouse, UPS, F-31400 Toulouse, France
Keywords:
Diagnosis, Parameter Estimation, Nonlinear Systems, Interval Analysis.
Abstract:
Through parameter estimation schemes, one could be able to detect, localize and identify the occurring fault
via simple computation. Yet, certain faults may not be discovered even be mistaken in a normal condition
with unknown noises by trend checking or state monitoring. A more informative way when a correct model
is present to analyses the data via parameter estimation. In this paper, we propose by using interval analysis
a diagnosis scheme, from which we can extract the guaranteed diagnostic results to inform the supervisor so
that appropriate actions could be taken. Sending them the results in a guaranteed way to tell the diagnostician
which kind of fault exist is firstly taken care in diagnosis context. Our original fault detection and localiza-
tion procedure has been firstly proposed in an interval analysis context for the constant fault in parameters.
Moreover, another new technique in parameter estimation is the distance check, which speed up the estimation
procedure. Some drawbacks have been discussed in the end.
1 INTRODUCTION
The fault detection, isolation and identification is a
key aspect in the reinforcement of the manipulability
of operation systems. Generally, the fault is consid-
ered as a nonpermitted deviation from an expectora-
tion process, a value from sensors, outputs. These
monitoring measurable variables in some supervisor
mechanism can be very difficult to implement (Bailey,
1984). Moreover these surveillance technique does
not allow a profound investigation to fault diagnosis
(Isermann, 1993). Even if one or more deviations
are found, no further information on which actuator
or which sensor is needed to be taken care of. Such
situation requires more sophisticated methods to ex-
tract information based on measurements. To do this,
methods such as state estimation diagnosis, parameter
estimation diagnosis and fault model diagnosis have
been developed (Isermann, 2005).
In stochastic case, the diagnosis could be arrived
by using the confidence interval to prove the correct-
ness and the failure mode in case of some extreme
situation occurs. This intervals are some times very
large that one could no further rely on. In the mean
time, the so called estimated value has intrinsic value
error due to the model inaccuracy and data uncer-
tainty, which shadow the estimated results for further
usage.
When dealing with fault detection and identifi-
cation (FDI) problem, particularly for process mod-
els, parameter estimation method is the first to con-
sider. The computational simplicity and direct under-
standable parameter information make it very popular
among the diagnostician. Whereas, the main draw-
backs of parameter estimation techniques are their
weak robustness to external disturbances as one have
to set a nominal value to start searching (Jauberthie
et al., 2013) and also, the identifiability of a studied
system must be done at first. With interval analysis
approach, no more identifiability information is re-
quired for parameter estimation (Jaulin and Walter,
2001) in general. The simplicity of implementation
and applicable for a large range of system make this
approach popular in automatic control field (Jaulin,
2001). Whereas, a great consumption of computation
time of such method is inevitable (Jaulin and Walter,
1993) due to the inner brand and bound solution find-
ing scheme which limits the diagnostic capabilities
(fault size, appearance time, etc.) (Isermann, 1984)
(Cimpoesu et al., 2012). Once the parameter is ob-
tained, the diagnostic procedure is completed by two
steps: the comparison between the quantities obtained
from actual model and the normal system. The fault
will be detected by using some range decision or in-
330
Li Q., Jauberthie C., Denis-Vidal L. and Cherfi Z..
A Diagnosis Scheme for Dynamical Systems: Approach by Guaranteed Parameter Estimation.
DOI: 10.5220/0005572703300335
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 330-335
ISBN: 978-989-758-122-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

tersection computation. Next step is the fault identi-
fication. The faults may be classed according to its
form, the corresponding reactions will be taken ac-
cording to the fault tree. If the fault is tolerable, the
system may continue functioning with a fault model
or if a full stop is needed and a sound diagnosis is
required to eliminate the fault.
In this paper, parameter estimation based fault di-
agnosis procedure is described. Only single fault dur-
ing each experiment is considered. To address the
fault condition as soon as possible, a distance based
method has been proposed. This new elimination
method originally proposed in interval analysis con-
text allowing us to find the unfeasible parameter as
soon as the output abnormality observed.
This paper is organized as follows: Section 2 will
give a brief explication on the treating problem in set
membership context, the general idea of parameter es-
timation approach in interval analysis. In section 3,
the guaranteed diagnosis procedure via parameter es-
timation is firstly proposed. In section 4, a case study
is conducted, the so called method has been compared
with results obtained with normal condition. At last,
the section 5 will give a brief summary on active di-
agnosis and further research direction. Some notices
of use has delivered.
2 MODEL-BASED DIAGNOSIS
This article follows the standard notation of interval
analysis (Kearfott et al., 2005) where x in bold refer-
ring to an interval box. Let us consider a nonlinear
dynamic system of the following form:
˙x(t, p) = f (x(t), p, u(t)),
y(t, p) = h(x(t, p)).
(1)
where x(t) ∈ IR
n
and y(t) ∈ IR
m
denote respec-
tively the state variables and the measured outputs.
u(t) is the system input. The initial conditions x(0)
is supposed to belong to an initial bounded ”box”
x
0
= [x
0
, x
0
]. The parameter vector p is constant and is
assumed to belong to a bounded ”box” p
0
= [p
0
, p
0
].
Time t is assumed to belong to [0, t
max
]. The functions
f and h are nonlinear functions. f is real and analytic
on M for every p ∈ P
0
, where M is an open set of R
n
such that x(t) ∈ M for every p ∈ P
0
and t ∈ [0, t
max
]).
Moreover the function f is assumed to be sufficiently
differentiable in the domain M.
In diagnosis context via parameter estimation ap-
proach, the system parameters have always some con-
nections with state deviation or physical meanings.
A fully rigorous and easy implementable procedure
to estimate the abnormality of parameters or states
should be taken into account.
The parameter estimation procedure is based on
set membership computation which is concerning to
find p such that y
m
(p) fits best in an inclusion test to
be specified. The parameters are considered consis-
tent if the error v(t
i
) is assumed to satisfy:
y(t
i
, ˆp) − y
m
(t
i
, p) ∈ v(t
i
) = [v(t
i
), v(t
i
)], i = 1, ..., N.
(2)
where y(t
i
) represents the output of system with exact
parameter ˆp and y
m
(t
i
) represents the measured out-
put, this inclusion is to be taken component-wisely.
We assume that v(t
i
) and v(t
i
) are known as lower and
upper bounds for the acceptable output errors. Such
bounds may, for instance, correspond to a bounded
measurement noise. The integer N is the total number
of sample times.
Interval analysis provides tools for comput-
ing with sets which are described using outer-
approximations formed by union of non-overlapping
boxes. Some basic tools on interval analysis are pro-
posed in (Li et al., 2014).
3 GUARANTEED FAULT
DIAGNOSIS
The word ”guaranteed” is referring to a parameter es-
timation (detection) phase in diagnosis. Generally,
the model based diagnosis could be achieved by com-
paring the behaviors from the real output of a pro-
cess and the model output, where is later is obtained
from state estimator (Gertler, 1998) (Isermann, 1993).
To ensure a fault is actually arrived, one has to check
with an occurrence counter or a redundant acceptance
scheme to make sure that indeed a fault is arrived.
Thus, a rigorous and robust method could be used,
which detects and confirms the fault in one shot. In-
terval analysis computes with guaranteed bounds to-
gether with a rigorous solver is a good tool to realize
the job.
A general process for FDI in interval analysis may
be conducted by three essential steps:
1. Detect the faults from the measurements via pa-
rameter estimation
2. Locate the faults
3. Identification of faults, its frequency or magni-
tude.
The first step should make the data in bounded
form. This could be done by adding the bound er-
ror to the measured data. Then, guaranteed parameter
ADiagnosisSchemeforDynamicalSystems:ApproachbyGuaranteedParameterEstimation
331

estimation procedure is conducted on observed quan-
tities. At last, the obtained sets intersect with admis-
sible parameter range to check if an error appears.
In practice, suppose that the acceptable range of
parameters is represented by p and the estimated ac-
ceptable range of parameters in each diagnosis is rep-
resented by ˆp. So, the residual part of two sets can be
represented by:
r = ˆp ∩ p. (3)
If the intersection part r =
/
0, a fault is detected.
In the diagnosis context, the deviation of the
model output and the real output of the studied sys-
tem can be described by the distance (Equ 4). This
indicator could be served as a tool in the second place
(step 2) to evaluate if one solution sets if enough close
to one another. One possible tool is the middle points
distance, which could be described by the following
formula:
D(y(t
i
) − y
m
(t
i
, p)) = |m(t
i
, y) − m(y
m
(t
i
, p))|, (4)
A direct use of this criterion to eliminate certain
points is inappropriate. The width information will
lost due to the midpoint measurement. Another pos-
sible tool is Hausdorff distance H(·), which is given
by:
H(y(t
i
), y
m
(t
i
, p)) = |m(y(t
i
)) − m(y
m
(t
i
, p))|+
|rad(y(t
i
)) − rad(y
m
(t
i
, p))|
(5)
Suppose we have the two sets of value, this dis-
tance could be useful to drag out the unfeasible points.
Proposition. There are two sets of parameters p
1
and
p
2
, if the distance difference between them are satis-
fying:
Dist(y − y
m
(p
1
)) − Dist(y − y
m
(p
2
)) > C, (6)
where C is a constant, Dist(·) =
∑
N
i=1
D(·) or
Dist(·) =
∑
N
i=1
H(·), N represents the number of avail-
able points. We can say that the p
1
is an unfeasible
set, because it is sufficiently away from the measure-
ments.
As we can see, sometimes the solution from mid-
dle points happens to be in the solution sets, so its
distance with measurements may be very small. Any
other sets of parameters have larger value than it. So
the value of C is always be settled large to avoid such
situation.
The following procedure may be integrated in
parameter estimation algorithm (Li et al., 2014),
as there is no initial computation to calculate this
midpoint distance:
Algorithm 1 : Distance criterion elimination (y,
h([x
e
(1 : j)])), Dist
pre
).
Input: x
e
;
Output: P
re jected
;
1: if Dist(y, h([x
e
(1 : j)])) − Dist
pre
> C then
2: P
re jected
:= P
re jected
∪ p;
3: else
4: Dist
pre
:= Dist(y, h([x
e
(1 : j)]))
5: end if
where x
e
= [x, p], j represents the value of x(t
j
) .
When first use of this algorithm, Dist
pre
is initial-
ized by 0. This algorithm requires no extra writing of
system sensitivity equation. All information needed
is available and must calculated for the set inversion
procedure after.
In interval analysis context, the parameter estima-
tion requires an inclusion test to separate the feasible
and unfeasible sets. All the feasible p ∈ P must sat-
isfy:
y
m
(t, p) ∈ y = [y(t), y(t)] (7)
where y
m
(t, p) presents the model output, y repre-
sents the actual measurement. This test is time con-
suming. A contractor could be applicable to reduce
the computation time. When there is an analytical
output model exists, one could use a contractor like:
Newton, Krawczyk to eliminate the unfeasible boxes.
Or, if no such model is available, we can use a mean
value form to represent the inclusion test (Kieffer and
Walter, 2011) with more computation effort on sen-
sitivities parts, so that a new parameter set could be
achieved by displacing the p
j
to one side.
In the following section, we will use the distance
check to replace the contractor in parameter estima-
tion algorithm, and a comparison of execution time
between the method set inversion with contractor, the
method set inversion with distance elimination, the
method uses only set inversion will be compared and
commented.
4 APPLICATION
The results are obtained using a Core i7 at 3.6GHz
with 8G RAM on a Linux system. The state estima-
tion is using VNODE-LP. Single permanent fault in
constant parameters is considered, but multiple faults
are also admissible for such solution scheme.
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
332
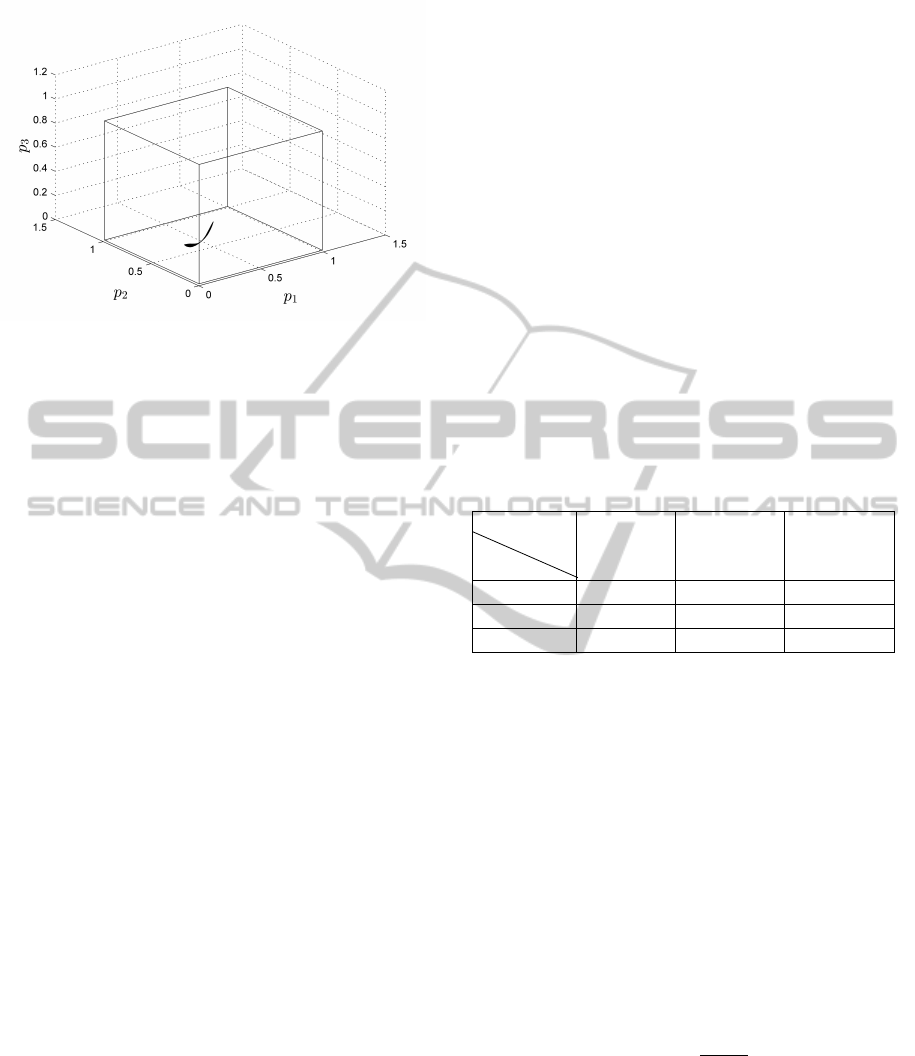
Figure 1: Outer approximation of admissible sets for p
1
, p
2
and p
3
4.1 Two Compartments Model
The case study that we consider is a linear compart-
ment system, which has been studied in (Kieffer and
Walter, 2011).
˙x
1
= −(p
1
+ p
3
)x
1
+ p
2
x
2
+ u
˙x
2
= p
1
x
1
− p
2
x
2
(8)
the fault parameter is appeared on p
1
at the begin-
ning of time, which is considered to be equal with
0.2 as a fault in system, the other parameters are
p
2
= 0.15 and p
3
= 0.35. Besides, the initial state is
x
1
= 1 and x
2
= 0, assume there is no input. We gener-
ate the faulty measurements with these configuration
over every second in t = 15 s and add a constant in-
terval noise v = [−0.005, 0.005]. In normal situation,
we know ˆp
1
∈ [0.5891, 0.6115] considering the mea-
surement error. The parameter estimation step should
give us a necessarily good estimation for p
1
so that
this fault may be detected and isolated with other po-
tential faults in diagnosis procedure. In this paper, we
will also be interested in time efficiency.
The parameter space is supposed to be included in
p ∈
0.01 1.0
0.01 1.0
0.01 1.0
. (9)
The stop criterion is supposed to ε = 0.0005. We
set C = 0.85 for the midpoint distance method. The
three parameters are projected to the 3-D dimension
plan. Only the admissible and rejected sets are pic-
tured of interest. The blue parts represent the unfeasi-
ble sets (Fig. 1). As we are seeing a 3D figure from a
2D view point, the more the parts superposed, darker
color they will get.
To be clear, the obtained admissible parameters
are equal with:
p
admis
∈
0.1889, 0.2121
0.1241, 0.4267
0.1241, 0.4267
(10)
As we can see, the parameter has no intersection
between the admissible parameter p
1
and ˆp
1
. The
constant fault appeared on parameter p
1
has been de-
tected. To identify the fault, the Hausdorff distance
can be useful to make a decision map so that cer-
tain actions could be taken. In this case, we have
H(p
1
, ˆp
1
) = 0.4002. Based on the distance informa-
tion, we need to check the conveyance tunnel as a
lower transfer rate is observed.
As the identification step is not time consuming,
it is clear that if the parameter estimation process
could be faster, better diagnosis performance could be
achieved. Here, we use the proposed approach with
other methods to show their different time consump-
tions :
Table 1: Time consumption for each configuration of pa-
rameter estimation.
ε
Time (s)
SIVIA
Distance
check
SIVIA
with Con-
tractor
0.005 29 27 147
0.001 144 124 3781
0.0005 548 496 16089
The column SIVIA represents the parameter esti-
mation is achieved by algorithm proposed in (Li et al.,
2014). We can conclude that with the distance check,
the time for parameter estimation can be relatively re-
duced. The contractor may delay the whole process
when precise bounding is required. A moderate us-
age of contractor is needed, one could use the distance
criterion as the start condition for contractor or some
other volume criterion could be also helpful.
4.2 Pharmaceutical Model
Let us consider a nonlinear model about glucose-
oxydase pharmacokinetics studied by (Verdiere et al.,
2005). The system is given by:
˙x
1
= k
12
(x
2
− x
1
) − k
v
x
1
1 + x
1
, x
1
(0) = x
10
,
˙x
2
= k
21
(x
1
− x
2
), x
2
(0) = 0,
y = x
1
.
(11)
Where x
1
is the enzyme concentration in plasma
(compartment 1), x
2
is concentration in compartment
2 and k
12
is the rate constant of the transfer from com-
partment 1, practically plasma, to compartment 2, is
the sum of all the transcapillary transfers in all the
ADiagnosisSchemeforDynamicalSystems:ApproachbyGuaranteedParameterEstimation
333

organs. Furthermore, k
21
is the rate constant of the
transfer from compartment 2 to compartment 1, k
v
is the maximum rate of an uptake by macrophages
through the mannose receptor. The receptor-mediated
uptake is a cellular process taking place at the level of
the macrophage membrane. The parameters to be es-
timated are p = [k
12
, k
21
, k
v
] which are assumed to be
uncertain.
The initial condition is supposed to x
1
= 1 and
the measurement is only available on x
1
. The fault is
supposed single and no time variant, already existed
before the diagnosis, which indicating k
v
= 0.092 at
t = 0. The interchange parameters are supposed to
k
12
= 0.011 and k
21
= 0.02 which are in right value.
Knowing that the right parameters are equal to p =
[0.011, 0.02, 0.1]. Under the measurements error as-
sumption v = [−0.005, 0.005] over all time, we know
that
ˆ
k
v
∈ [0.0974, 0.1026]. For a global consideration
of any other fault, we set the a priori parameter inter-
val as following :
p =
0.0099, 0.0121
0.018, 0.022
0.08, 0.11
. (12)
The sampling time is t = 117s and we measure the
x
1
at every second. The following figures have been
obtained by the same parameter estimation algorithm
with ε = 0.0001. Smaller values have been tested by
no more obvious improvement in quantity of accept-
able sets are obtained. The results for admissible sets
are presented in figure 2. The admissible sets for each
parameter are supposed to be included in:
p
admis
∈
0.0099, 0.0121
0.0180, 0.0220
0.0891, 0.0948
(13)
The fault parameter has been well localized as
the intersection of admissible sets for k
v
between
the estimated parameter and the a priori known pa-
rameter is empty which refers to a fault. Besides,
as the k
v
= [0.0891, 0.0948] is resided completely in
unacceptable parts, this resolution of fault distinc-
tion could be described by the Hausdorff distance
H(p
3
, ˆp
3
) = 0.0083. Next, a fault tree which indicates
the level of fault and gives corresponding actions.
In the figure 2, the searching domain of k
12
and
k
21
are full filled with acceptable boxes, which im-
plies that the measurement has too big error or the
sampling time is not sufficient, that set inversion al-
gorithm is not able to generate the solution with such
data. Such situation will be problematic during mul-
tiple occurrence of fault. Besides, it may happen that
the intersection of estimated parameter and the admis-
sible right parameter is not empty. To ameliorate this
Figure 2: Outer approximation of admissible sets of k
12
, k
21
and k
v
.
phenomena, one could use an optimal input design or
an optimal initial state design to get better estimated
results from presumed bounding errors on system out-
put or use more accurate sensors. As we are seeing
a 3D figure from a 2D view point, the parts are su-
perposed, the ones in the middle are darker than the
outsides.
We have tried different configurations for parame-
ter estimation, the distance check technique combines
the parameter estimation procedure is the optimal one
in term of time efficiency, see Table 2.
Table 2: Time consuming for each configuration of param-
eter estimation.
ε
Time (s)
SIVIA
Distance
check
SIVIA
with
Contractor
0.0005 10 9 13
0.0001 321 310 4897
0.00005 1267 1242 18972
5 CONCLUSION
The original proposed diagnosis procedure using set
inversion of interval analysis may be an effective tool
to detect, localize and identification of fault. The pro-
posed distance check is the first talked about in such
context. The only question is the choice of C which is
experimental. In practice, as the diagnosis is off line,
one could start with a value compared to the sum of
width on error bounds of measurement, decreasing it
when no more pessimistic solutions are mistaken.
In diagnosis, a guaranteed solution is always use-
ful to localize surely the faulty parameters. With
enough precision and multi fault occurrences on es-
timated results, this information could be evaluated
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
334

through a fault tree analysis. According to the pre-
sumption made on the error bound, the results are
fully rigorous.
In this paper, we proposed an original diagno-
sis procedure, the distance check technique is at the
first time talked about, which helps to eliminate the
unfeasible sets more efficiently in parameter estima-
tion context using interval analysis. Comparing other
available methods, one could use our approach to get
a more rapid parameter estimation. Similar to the con-
tractor with set inversion algorithm, this technique is
useful when the unacceptable parts are large of the
initial search domain. If it is not the case, one have to
use other optimization methods to obtain the results
more quickly.
REFERENCES
Bailey, S. (1984). From desktop to plant floor, a crt is the
control operators window on the process. Control En-
ginerring, 31(6):86–90.
Cimpoesu, E., Ciubotaru, B., and Stefanoiu, D. (2012).
Short investigation on system diagnosis regarding pa-
rameter estimation. In Systems and Computer Science
(ICSCS), 2012 1st International Conference on, pages
1–6. IEEE.
Gertler, J. (1998). Fault detection and diagnosis in engi-
neering systems. CRC press.
Isermann, R. (1984). Process fault detection based on mod-
eling and estimation methods - a survey. Automatica,
20(4):387–404.
Isermann, R. (1993). Fault diagnosis of machines via pa-
rameter estimation and knowledge processing?tutorial
paper. Automatica, 29(4):815–835.
Isermann, R. (2005). Model-based fault-detection and
diagnosis–status and applications. Annual Reviews in
control, 29(1):71–85.
Jauberthie, C., Verdi
`
ere, N., and Trav
´
e-Massuy
`
es, L.
(2013). Fault detection and identification relying on
set-membership identifiability. Annual Reviews in
Control, 37:129–136.
Jaulin, L. (2001). Applied interval analysis: with examples
in parameter and state estimation, robust control and
robotics, volume 1. Springer.
Jaulin, L. and Walter, E. (1993). Set inversion via interval
analysis for nonlinear bounded-error estimation. Au-
tomatica, 29(4):1053–1064.
Jaulin, L. and Walter, E. (2001). Nonlinear bounded-error
parameter estimation using interval computation. In
Granular computing, pages 58–71. Springer.
Kearfott, R., Nakao, M., Neumaier, A., Rump, S., Shary, S.,
and Van Hentenryck, P. (2005). Standardized notation
in interval analysis.
Kieffer, M. and Walter, E. (2011). Guaranteed estimation
of the parameters of nonlinear continuous-time mod-
els: Contributions of interval analysis. International
Journal of Adaptive Control and Signal Processing,
25(3):191–207.
Li, Q., Jauberthie, C., Denis-vidal, L., and Cherfi, Z. (2014).
Guaranteed state and parameter estimation for nonlin-
ear dynamical aerospace models. In Informatics in
Control, Automation and Robotics (ICINCO), 2014
11th International Conference on, volume 01, pages
519–527.
Verdiere, N., Denis-vidal, L., Joly-blanchard, G., and Do-
murado, D. (2005). Identifiability and estimation
of pharmacokinetic parameters for the ligands of the
macrophage mannose receptor. International Jour-
nal of Applied Mathematics and Computer Science,
15:517–526.
ADiagnosisSchemeforDynamicalSystems:ApproachbyGuaranteedParameterEstimation
335
