State-parameter Dependency Estimation of Stochastic Time Series using
Data Transformation and Parameterization by Support Vector
Regression
Elvis Omar Jara Alegria, Hugo Tanzarella Teixeira and Celso Pascoli Bottura
Semiconductors, Instruments, and Photonics Department, School of Electrical and Computer Engineering,
State University of Campinas - UNICAMP, Av. Albert Einstein, N. 400 - LE31 - CEP 13081-970, Sao Paulo, Brazil
Keywords:
Time Series Identification, State-dependent Parameter, Support Vector Regression.
Abstract:
This position paper is about the identification of the dependency among parameters and states in regression
models of stochastic time series. Conventional recursive algorithms for parameter estimation do not provide
good results in models with state-dependent parameters (SDP) because these may have highly non-linear
behavior. To detect this dependence using conventional algorithms, we are studying some data transformations
that we implement in this paper. Non-parametric relationships among parameters and states are obtained and
parameterized using support vector regression. This way we look for a final non-linear structure to solve the
SDP identification problem.
1 INTRODUCTION
The regression models with SDP, called SD-ARX
(Priestley, 1988) or quasi-ARX (Hu et al., 2001),
are always non-linear due to the product between
the regressor function and the SDP. Young proposed
a limited and approximated but useful solution to
SDP estimation (Young, 2006). It is based in a as-
cendant temporal data reordering to simplify the es-
timation process. This is based on the fact that
if this state-parameter dependence exists, then both
should react the same manner to this data reordering.
Young has shown that when the estimated parameters
are returned to the normal temporal order, then the
state-parameter dependence shape turned evident. Of
course, the nature of the reordering will affect the es-
timation and the ascending order is not always appro-
priate. A criterion to determine a good sorting could
be a function of the minimum variance estimates. But
then is it possible to find other data transformations
as well as data sorting that could simplify the model
response and satisfy the criteria of minimum variance
estimates?
The present paper proposes data transformations
for SDP estimation. Such as Young’s data sorting can
simplify the rapid variation, the data transformations
is currently studied by us and find to simplify even
more the estimation process by bringing the data to a
constant value in the new data transformed space.
After to data transformation step, a non-
parametric relationship between model parameters
and model states is obtained. Various functions ap-
proximators are used to parametrize those relation-
ships technics. Widely used function approximators
are multilayer perceptrons, radial basis functions and
fuzzy models (Nørgaard et al., 2000). Usually the
identification of non-linear models is computationally
expensive due the fact that the optimization problem
is usually non-linear and non-convex. In addition, the
designer must trade off the expressiveness of the ar-
chitecture with the need to maintain computational
tractability.
To address these issues, we propose a approxima-
tion architecture based on the idea of support vec-
tor regression (SVR) (Smola and Sch
¨
olkopf, 2004).
The SVR solution is calculated via a convex pro-
gram which has a unique optimal solution, and be-
ing a kernel-based method, SVR can handle very
large numbers of basis functions in a computationally
tractable way.
2 SDP IDENTIFICATION
In this paper, the regression linear model with SDP
parameter is expressed by equation (1).
342
Omar Jara Alegria E., Tanzarella Teixeira H. and Pascoli Bottura C..
State-parameter Dependency Estimation of Stochastic Time Series using Data Transformation and Parameterization by Support Vector Regression.
DOI: 10.5220/0005574103420347
In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2015), pages 342-347
ISBN: 978-989-758-122-9
Copyright
c
 2015 SCITEPRESS (Science and Technology Publications, Lda.)

y(k) = z
T
(k)ρ(k) + e(k); e(k) = N(0, σ
2
) (1)
where,
z
T
(k) =
h
−y(k −1) −y(k − 2) ··· −y(k −n)
u(k −δ) · · · u(k − δ − m)
i
ρ(k) =
h
a
1
{
X (k)
}
a
2
{
X (k)
}
··· a
n
{
X (k)
}
b
0
{
X (k)
}
··· b
m
{
X (k)
}
i
T
ρ(k) =
h
ρ
1
{
X (k)
}
ρ
2
{
X (k)
}
··· ρ
n+m+1
{
X (k)
}
i
T
The regression vector z(k) ∈ R
n+m+1
is composed
of the measurement y(k) ∈ R and of the exogenous
input u(k) ∈ R. The SDP ρ
i
∈ R, i = 1, 2, ...n + m + 1,
related to the parameters a
i
or b
i
, are assumed to be
functions of some variable in a non-minimal state vec-
tor X
T
(k) =

z
T
(k) U
T
(k)

. Here U(k) is a vector
of other variables that may affect the relationship be-
tween these two primary variables, ρ
i
and X (k), e.g. a
regressors combination. Also, δ is a pure time delay
on the input variable and e(k) is a zero mean, white
noise. To simplify, let’s suppose that each SDP is a
function of only one state variable.
The Simple Fixed Interval Smoothing (SFIS) is
a simple but useful estimation algorithm to solve 1.
This can be obtained by a combination of the recur-
sive estimate with forward data and backward data,
i.e. with data from sample k to N and from N to k
respectively. To allow the TVP in each one of these
cases, an exponential windows past (EWP) with a for-
getting factor α is used (Alegria, 2015). An optimal
value of α can be obtained by the hyper-parameters
optimization (Young, 2011). This is the difference be-
tween the SFIS and the optimal FIS algorithms.
2.1 Young’s Reordering of Data
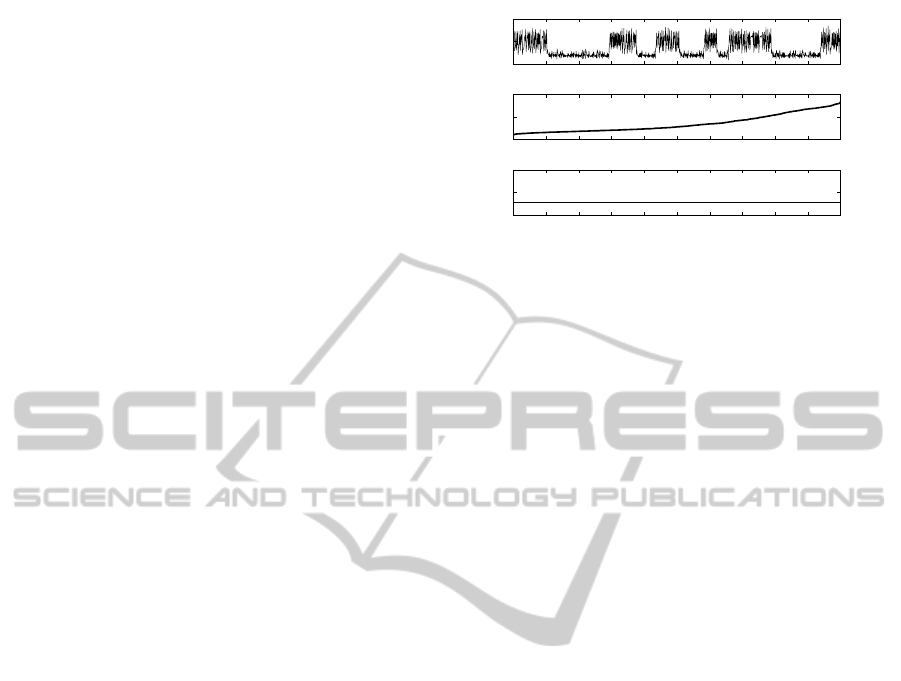
In this paper the temporal data reordering (TDR) is
considered as a temporal data transformation, where
only the time ordering is affected. It is yield to sim-
plify the estimation process decreasing the rapid vari-
ations on the state values x(k). In this case there
are two data observational spaces; the untransformed
space and the transformed space. Fig. 1 shows both
kinds of observation spaces. In the transformation
process, it’s important to save an original index vec-
tor, because this will be necessary to come back to the
original temporal order space or untransformed space.
2.2 Two Proposals of Data
Transformations
Data transformation refers to the application of a
known deterministic mathematical function to each
0 100 200 300 400 500 600 700 800 900 1000
−2
0
2
time
x(k)
0 100 200 300 400 500 600 700 800 900 1000
−2
0
2
reordered index of time
x*(k)
0 100 200 300 400 500 600 700 800 900 1000
−2
0
2
time
x*(k)
Figure 1: Time series in untransformed space (up), in tem-
poral data reordering TDR (middle) and using data transfor-
mation to the mean DTM (below).
point in the data set, i.e. each data point of X
j
=

x
j
1
x
j
2
. . . x
j
N

is replaced with the transformed
value x
∗
i
= f (x
i
), where f (.) is an appropriate math-
ematical function and (∗) represents the transformed
space (Dolby, 1963). To return to the untransformed
or original data, the inverse function x
i
= f
−1
(x
∗
i
) is
used. The particularity of our proposed transforma-
tions is that each point in the data has a different trans-
formation in order to obtain a smoothed transformed
value. Differently to the Young’s data reordering, our
transformed data is ideally smoothed. Where, by def-
inition, ideal smoothing is when x
∗
i
= ψ, i = 1, 2, ..., N,
where ψ is a constant value. Due to this ideal smooth-
ing, the transformed SDP will also be constant, be-
cause of the dependence between the SDP and the
state X
j
.
A simple linear function f (x
i
) = β
i
x
i
+ θ
i
; β ∈ R,
θ ∈ R, i = 1, 2, ..., N, and its respective inverse func-
tion f
−1
(x
∗
i
) = (x
∗
i
− θ
i
)β
−1
i
are used for the data trans-
formations. The function parameters vectors β =

β
1
β
2
. . . β
N

and θ =

θ
1
θ
2
. . . θ
N

are cal-
culated in order to obtain a constant value for x
∗
i
= ψ,
e.g. fixing β
i
= 1 then θ
i
= x
∗
i
− x
i
. Two different op-
tions, equals to the mean value ψ = E
{
X
j
(k)
}
and to
zero ψ = 0, are proposed. Fig. 1 (down) shows the
data transformation for the model (19), shown in the
numerical example, when ψ = E
{
X
j
(k)
}
is tested.
3 SUPPORT VECTOR
REGRESSION
This section provides a basic overview of support
vector regression; for more details, see (Smola and
Sch
¨
olkopf, 2004). The objective of the SVR problem
is to learn a function.
f (x) = w
T
ϕ(x) (2)
State-parameterDependencyEstimationofStochasticTimeSeriesusingDataTransformationandParameterizationby
SupportVectorRegression
343

x
y
××
××
××
××
××
××
××
××
××
××
××
ξ
××
ξ
0
+ε
0
−ε
(a) A tube with radius ε is
fitted to the data for a one
dimensional linear regres-
sion problem.
y − f (x,w)
0
c
ε
(y, f (x, w))
−ε
+ε
××
ξ
××
ξ
0
(b) The linear ε-insensitive loss
function.
Figure 2: The soft margin loss setting for a linear SVR.
that gives a good approximation of a given set of
training data {x
i
, y
i
}
n
i=1
where x
i
∈ R
m
and y
i
∈ R is
the observed output, {ϕ
j
(x)}
m
b
j=1
is a set of nonlinear
basis functions that maps an input space into a fea-
ture space, the parameter vector w ∈ R
m
b
is unknown.
The problem is to compute estimates of w which min-
imizes the norm ||w||
2
= w
T
w. We can write this prob-
lem as a convex optimization problem:
minimize:
1
2
w
T
w
subject to: y
i
− w
T
ϕ(x
i
) ≤ ε
w
T
ϕ(x
i
) − y
i
≤ ε
i = 0, 1,. .. , n
(3)
The support vector (SV) method was first devel-
oped for pattern recognition. To generalize the SV
algorithm to the regression case, an analog of the soft
margin is constructed in the space of the observed
output y by using Vapnik’s ε-insensitive loss function
(Vapnik, 1995) described by
c(x, y, f (x)) := |y− f (x)|
ε
:= max{0,|y − f (x)| − ε} (4)
Fig. 2 depicts the situation graphically. Only the
points outside the shaded region contribute to the cost
insofar, as the deviations are penalized in a linear
fashion.
Now, we can transform the optimization problem
(3) by introducing slack variables, denoted by ξ
i
, ξ
0
i
.
Hence we arrive at the formulation
minimize:
1
2
w
T
w +C
n
∑
i=0
(ξ
i
+ ξ
0
i
)
subject to: y
i
− w
T
ϕ(x
i
) ≤ ε + ξ
i
w
T
ϕ(x
i
) − y
i
≤ ε+ξ
0
i
ξ
i
, ξ
0
i
≥ 0
i = 0, 1,. .. , n
(5)
where, the regularization term
1
2
w
T
w penalizes model
complexity, and C is a non-negative weight which de-
termines how much prediction errors which exceed
the threshold value ε are penalized.
The minimization problem (5) is difficult to solve
when the number n is large. To address these issue,
one can solve the primal problem through its dual,
which can be formulated finding a saddle point of the
associated Lagrange function (Vapnik, 1995)
L(w,ξ, ξ
0
, α, α
0
, β, β
0
)
=
1
2
||w||
2
+C
n
∑
i=0
(ξ
i
+ ξ
0
i
) −
n
∑
i=0
(β
i
ξ
i
+ β
0
i
ξ
0
i
)
+
n
∑
i=0
α
i
(y
i
− w
T
ϕ(x
i
) − ε − ξ
i
)
+
n
∑
i=0
α
0
i
(w
T
ϕ(x
i
) − y
i
− ε − ξ
0
i
) (6)
which is minimized with respect to w, ξ
i
and ξ
0
i
and maximized with respect to Lagrange multipliers
α
i
, α
0
i
, β
i
, β
0
i
≥ 0. It fallows from the saddle point con-
dition that the partial derivatives of L with respect to
the primal variables (w
i
, w
0
, ξ
i
, ξ
0
i
) have to vanish for
optimality.
∂
w
L = w −
n
∑
i=1
(α
i
− α
0
i
)x
i
= 0, (7)
∂
ξ
i
L = C −α
i
− β
i
= 0, (8)
∂
ξ
0
i
L = C −α
0
i
− β
0
i
= 0, (9)
i = 1, .. ., n
∂
w
0
L =
n
∑
i=0
(α
i
− α
0
i
) = 0 (10)
Substituting (7)–(10) into (6) yields the dual opti-
mization problem.
maximize: −
1
2
n
∑
i, j=0
(α
i
− α
0
i
)(α
j
− α
0
j
)ϕ(x
i
)
T
ϕ(x
j
)
+
n
∑
i=0
(α
i
− α
0
i
)y
i
− ε
n
∑
i=0
(α
i
+ α
0
i
)
subject to:
n
∑
i=0
(α
i
− α
0
i
) = 0
0 ≤ α
i
, α
0
i
≤ C
i = 0, 1,. .. , n
(11)
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
344

In deriving (11) we already eliminated the dual vari-
ables β
i
, β
0
i
through conditions (8) and (9). Eq. (7) can
be rewritten as follows
w =
n
∑
i=1
(α
i
− α
0
i
)ϕ(x
i
) (12)
The corresponding Karush-Kuhn-Tucker (KKT)
complementarity conditions are
α
i
(y
i
− w
T
ϕ(x
i
) − ε − ξ
i
) = 0 (13)
α
0
i
(w
T
ϕ(x
i
) − y
i
− ε − ξ
0
i
) = 0 (14)
ξ
i
ξ
0
i
= 0,α
i
α
0
i
= 0 (15)
(α
i
−C)ξ
i
= 0,(α
0
i
−C)ξ
0
i
= 0 (16)
i = 0, 1,. .. , n
From (13) and (14) it follows that the Lagrange mul-
tipliers may be nonzero only for |y
i
− f (x
i
)| ≥ ε; i.e.,
for all samples inside the ε-tube (the shaded region
in Fig. 2(a)) the α
i
, α
0
i
vanish. This is because when
|y
i
− f (x
i
)| < ε the second factor in (13) and (14) is
nonzero, hence α
i
, α
0
i
must be zero for the KKT con-
ditions to be satisfied. Therefore we have a sparse
expansion of w in terms of x
i
(we do not need all x
i
to describe w). The samples that come with nonva-
nishing coefficients are called support vectors. Thus
substituting (12) into (2) yields the so-called support
vector expansion
f (x) =
n
sv
∑
i=0
(α
i
− α
0
i
)ϕ(x
i
)
T
ϕ(x) (17)
where n
sv
is the number of support vectors. Now, a
final note must be made regarding the basis function
vector ϕ(x). In (11) and (17) it appear only as inner
products. This is important, because in many cases a
kernel function K(x
i
, x
j
) = ϕ(x
i
)
T
ϕ(x
j
) can be defined
whose evaluation avoids the need to explicitly calcu-
late the vector ϕ(x). This is possible only if the kernel
function satisfy the Mercer’s condition, for more de-
tails see (Sch
¨
olkopf and Smola, 2001).
3.1 Deriving the State-dependent
Parameter Model
Suppose that after the SDP estimation algorithm we
have obtained a relationship between a parameter ρ
j
and a state X
j
(k). Now, we can obtain a parametric
model of this relationship using the SV method. Thus,
we can rewrite (17) as
ˆ
ρ
j
(k) =
n
sv
∑
l=0
(α
l
− α
0
l
)K(z
j,l
, z
j
) (18)
where the Lagrange multipliers α, α
0
and the number
of support vectors n
sv
are obtained solving the opti-
mization problem (11). Note that the inner product
already was replaced by a kernel function.
4 NUMERIC EXAMPLE
Let the SDP model for pure stochastic time series be:
y(k) = z
T
(k)ρ(k) + e(k) (19)
where
z
T
(k) =
h
−y(k −1) −y(k − 2) ··· −y(k −n)
i
ρ(k) =
h
a
1
{
X (k)
}
a
2
{
X (k)
}
··· a
n
{
X (k)
}
i
T
The model (19) is a special case of (1). For this spe-
cific example, let’s study the cosine map model:
y(k) = cos (2.8y(k − 1)) + 0.3y (k − 2) + e(k),(20)
y(k) = a
1
(k) + a
2
(k)y(k −2)+e(k)
where e(k) is a zero mean, white noise; the parameter
a
1
(k) = cos(2.8y (k − 1)) is a SDP that depends on the
state X
1
= y(k − 1) and the parameter a
2
(k) = 0.3 is a
constant.
This example initially focuses on the non-
parametric estimation step of the SDP algorithm
shown above. First, using temporal data reorder-
ing and an optimal FIS estimation (TDR-FIS) of the
CAPTAIN toolbox (Taylor et al., 2007), the Young’s
algorithm is tested. Next, we only change the opti-
mal FIS by SFIS estimation (TDR-SFIS). Finally our
two proposed transformations are tested using SFIS
estimation, to the mean (DTM-SFIS) and zero value
(DTZ-SFIS), and the results are discussed.
4.1 SDP Estimation using TDR with
FIS and SFIS
The data was generated based on the equation (20).
Later, the data was sorted to allow the application of
the optimal FIS algorithm. The estimation based on
TDR-FIS was obtained the CAPTAIN toolbox (Tay-
lor et al., 2007). This is based on temporal data re-
ordering and on the optimal FIS estimation algorithm.
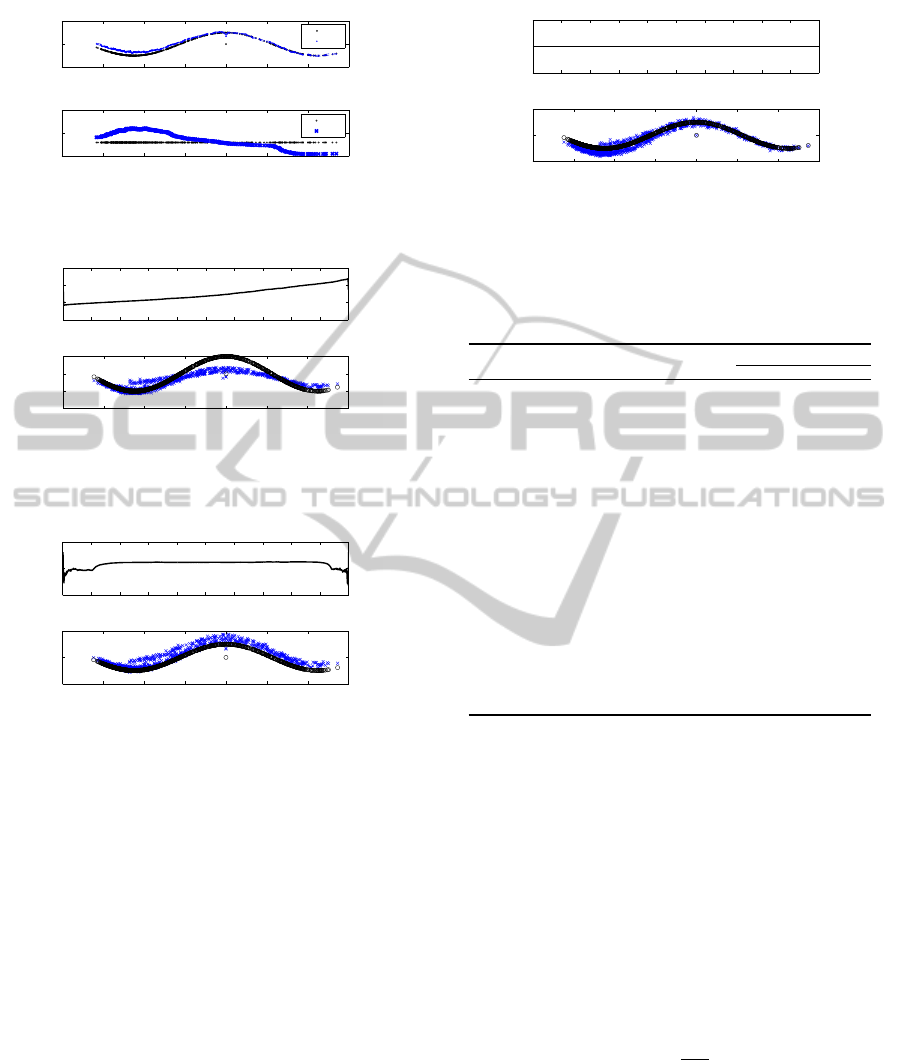
The Fig. 3 shows both parameter dependency estima-
tions; the first dependency is well detected. For the
second we can conclude that it does not exist, at least
for the analyzed state X
1
= y(k − 1).
In the case of estimation based on TDR-SFIS, the
result shown in Fig. 4 is obtained in a faster way, but
the result is not as good as the previous one.
4.2 SDP Estimation using DTM and
DTZ with SFIS
First, the estimation is based on DTM-SFIS, i.e do-
ing ψ = E
{
X
j
(k)
}
. Fig. 5 shows the SDP estimation
State-parameterDependencyEstimationofStochasticTimeSeriesusingDataTransformationandParameterizationby
SupportVectorRegression
345

−2 −1.5 −1 −0.5 0 0.5 1 1.5
−2
0
2
a
1
(k)
x
1
(k)
First state dependent parameter
par
sdp
−2 −1.5 −1 −0.5 0 0.5 1 1.5
0
0.5
1
a
2
(k)
x
2
(k)
Second state dependent parameter
par
sdp
Figure 3: SDP-FIS estimation using the CAPTAIN (blue)
and reference (black).
0 100 200 300 400 500 600 700 800 900 1000
−2
−1
0
1
Simple estimation smoothing
k
â
1
*(k)
−2 −1.5 −1 −0.5 0 0.5 1 1.5
−2
−1
0
1
Actual (red) and SFIS estimated (blue)
y(k−1)
â
1
y(k−1)
Figure 4: SDP-SFIS estimation of ˆa
∗
1
(k) using temporal
data reordering (up). Actual a
1
(down-black) and estimated
ˆa
1
(down-blue).
0 100 200 300 400 500 600 700 800 900 1000
−1
−0.5
0
SFIS estimation − DTM of the state y(k−1)
k
â
1 *
(k)
−2 −1.5 −1 −0.5 0 0.5 1 1.5
−2
0
2
SDP estimation − non transformed space
y(k−1)
â
1
y(k−1)
Figure 5: SFIS estimation of ˆa
∗
1
(k) using DTM (up-black).
Actual (down-black) and SDP estimated (down-blue).
results in the transformed space (up) and the depen-
dence among the transformed parameter ˆa
∗
1
and his re-
spective state-dependent y(k − 1) (down). Comparing
these results with the previous two, we can conclude,
for this specific example, that the DTM-SFIS case is
better than the TDR-SFIS shown in Fig. 4. But it’s
still not as good as the first one TDR-FIS estimation
shown in Fig. 3.
Fig. 6 shows the results for the DTZ-SFIS case
when the state values y(k −1) are transformed to zero:
ψ = 0. It’s easy to appreciate that the obtained result is
better than the previous one shown in Fig. 5, for ψ =
E
{
X
i
(k)
}
. Note that using ψ = 0 the SDP estimation in
the transformed space (up) ˆa
∗
1
is equal to zero such as
the initial state reordering y(k − 1) in the transformed
space. It is an obvious similarity because when both
parameters a
1
{
y(k − 1)
}
and b
0
{
u(k)
}
are zero, in the
equation model (19), then the measure y(k) also will
be zero in terms of least squares. Then the parameter
ˆa
1
is equals to y(k) and discovering the dependence
0 100 200 300 400 500 600 700 800 900 1000
−1
0
1
SFIS − Transformation to zero of y(k−1)
k
â
1
*(k)
−2 −1.5 −1 −0.5 0 0.5 1 1.5
−2
0
2
SDP in untransformed space
y(k−1)
â
1
y(k−1)
Figure 6: Estimation based on DTZ-SFIS of ˆa
∗
1
(k) using
ψ = 0 (up-green). Actual (down-black) and SFIS estimated
(down-blue).
Table 1: Identification results for numeric example using
standard SVR models and SVR models for state-dependent
parameters after data transformation.
Method ε NSV MSE (y − ˆy) MSE (a
1
− ˆa
1
)
Test set Real value
Standard SVR 0.1 613 0.1729 - -
0.2 443 0.1778 - -
0.3 386 0.1781 - -
0.4 257 0.1845 - -
TDR 0.1 343 0.1560 0.0212 0.1662
0.2 87 0.1914 0.0219 0.2238
0.3 63 0.2253 0.0655 0.2796
0.4 15 0.3341 0.0483 0.3970
DTM 0.1 345 0.2621 0.0336 0.2379
0.2 193 0.3471 0.0369 0.3090
0.3 123 0.3595 0.0655 0.3190
0.4 47 0.3581 0.0515 0.3290
DTM-unbiased 0.1 345 0.0431 - 0.0761
0.2 193 0.0230 - 0.0743
0.3 123 0.0099 - 0.0955
0.4 47 0.0272 - 0.1347
DTZ 0.1 407 0.0344 0.0380 0.0718
0.2 152 0.0281 0.0376 0.0842
0.3 92 0.0201 0.0444 0.1011
0.4 51 0.0297 0.0547 0.1413
between the SDP ˆa
1
and the state y(k − 1) consists in
discovering the phase plane between y(k) and the state
y(k − 1).
The results obtained after SVR application are
summarized in Table 1. The model complexity was
chosen as C = 400 by cross-validation tests for all
cases. For comparison, the standard SVR was also
applied to problem, where (20) was directly approxi-
mate using (17). The accuracy ε, the number of sup-
port vectors (NSV) and the mean-square errors (MSE)
of the prediction error and the model parameters are
shown. In all examples, kernel functions were taken
as gaussian kernels, i.e.:
K(z
j,l
, z
j
) = exp

−
1
2σ
2
||z
j,l
− z
j
||
2

(21)
where σ = 0.5. In all cases, the data set were divided
in a training data set consisting of 700 data points and
a test data set consisting of 300 data points.
We can see in Fig. 7, although the SVR method
provides a good fit for covalidation test set, they do
not correspond with the actual behavior of the rela-
tionship between the parameter and the state, com-
ICINCO2015-12thInternationalConferenceonInformaticsinControl,AutomationandRobotics
346

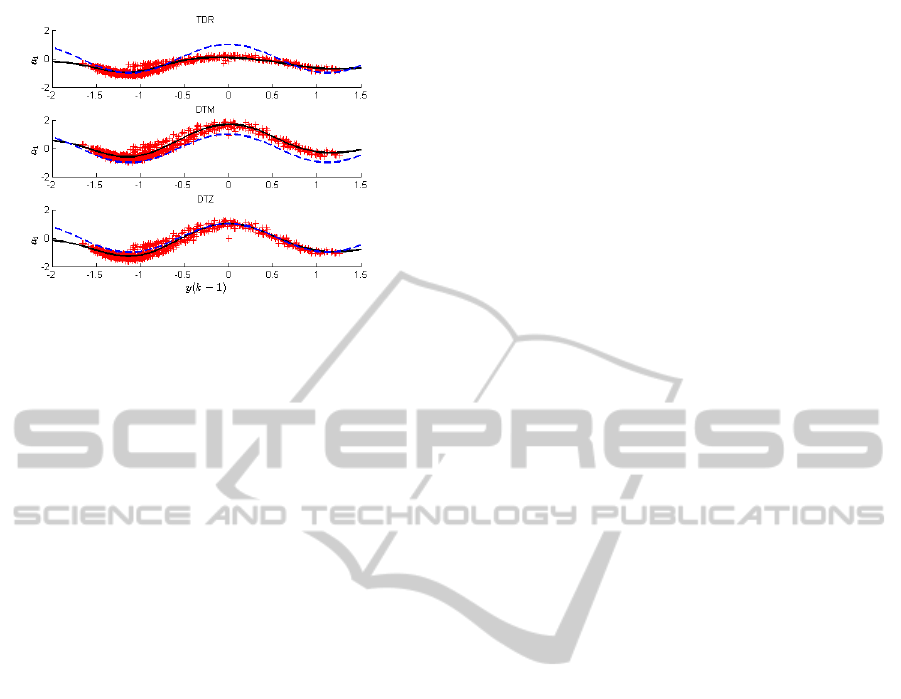
Figure 7: SVR parameterization for C = 400 and ε = 0.2
(black solid lines). The real state-parameter relationship
(blue dotted lines).
promising the good performance in the estimation of
the output.
In DTM case the state values y(k − 1) are trans-
formed to its mean, for ψ = E{X
i
(k)}. When the data
are reordered some bias appears, as we can see in
second plot in Fig. 7. The bias can be subtracted
by adding the difference between the mean of the
reordered data and the original data. Now DTM-
unbiased and DTZ methods results in similar perfor-
mances to estimate the output, see Table 1.
5 CONCLUSIONS
Parameter estimation methods based on recursive
least square are inefficient when the model presents
SDP. It is because the parameter and his respective
state vary very fast. Young shows an approximated
solution based on temporal data reordering and fixed
interval smoothing TDR-FIS. This TDR smooths the
state and the associated parameter. Both signals, state
and parameter, are assumed smoothed since the de-
pendence exists. Numerical example shows that TDR
is efficient only with an optimal FIS algorithm instead
of an SFIS, see Fig. 3 and Fig. 4. Unlike the TDR,
our two proposed transformation brings the data to a
constant value. The first brings the state to the mean
and the other to zero. These methods are called DTM
and DTZ respectively. The supposed constant param-
eter in the transformed space allow the use of SFIS
algorithm instead of an optimal FIS.
Numerical example shows that DTM and DTZ
both with SFIS estimation algorithm are equally effi-
cient to detect dependence on the SDP. SVR methods
was employed to parametrize and to obtain an error
measure for each transformation case. Based on the
result of Table 1, we can conclude that DTM-SFIS
and DTZ-SFIS are equally efficient to detect depen-
dence among state and parameter and both are better
than the estimation using TDR-SFIS. Based on nu-
merical complexity or computational cost, we also
can conclude that the DTZ is better than DTM be-
cause a state is converted to zero and it simplifies a
lot the algorithm. A final and more accurate model
structure was obtained using parametrization based
on SVR on the equation 18. Although our results
are goods, other examples to demonstrate our prac-
tical proposal are necessary, e.g. implement our algo-
rithm in models with exogenous inputs or multi-state
parameter dependency.
ACKNOWLEDGEMENTS
We thank Brazilian agency CAPES for the financial
support.
REFERENCES
Alegria, E. J. (2015). Off-line state-dependent parame-
ter models identification using simple fixed interval
smoothing. In 12th International Conference on Infor-
matics in Control, Automation and Robotics ICINCO.
Dolby, J. L. (1963). A quick method for choosing a trans-
formation. Technometrics, 5:317–325.
Hu, J., Kumamura, K., and Hirasawa, K. (2001). A quasi-
ARMAX approach to modeling of nonlinear systems.
International Journal of Control, 74:1754–1766.
Nørgaard, M., Ravn, O., Poulsen, N. K., and Hansen, L. K.
(2000). Neural Networks for Modelling and Control
of Dynamic Systems. Springer Verlag, London.
Priestley, M. (1988). Non-linear and non-stationary time
series analysis. Academic Press, London.
Sch
¨
olkopf, B. and Smola, A. J. (2001). Learning with Ker-
nels: Support Vector Machines, Regularization, Opti-
mization, and Beyond. MIT Press, Cambridge, MA,
USA.
Smola, A. J. and Sch
¨
olkopf, B. (2004). A tutorial on support
vector regression. Statistics and Computing, 14:199–
222.
Taylor, C., Pedregal, D., Young, P., and Tych, W. (2007).
Environmental time series analysis and forecasting
with the captain toolbox. Environmental Modelling
& Software, 22(6):797–814.
Vapnik, V. N. (1995). The nature of statistical learning the-
ory. Springer-Verlag, New York.
Young, P. (2006). Nonlinear system modeling based on non-
parametric identification and linear wavelet stimation
of sdp models. 45th IEEE Conference on Decision &
Control, pages 2523–2528.
Young, P. C. (2011). Recursive Estimation and Time-Series
Analysis. Springer-Verlag, 2 edition.
State-parameterDependencyEstimationofStochasticTimeSeriesusingDataTransformationandParameterizationby
SupportVectorRegression
347