
Design and Implementation of an Espionage Network for
Cache-based Side Channel Attacks on AES
Bholanath Roy
1
, Ravi Prakash Giri
2
, Ashokkumar C.
1
and Bernard Menezes
1
1
Department of Computer Science, Indian Institute of Technology - Bombay, Mumbai, India
2
Department of Computer Science, Shri Mata Vaishno Devi University, Jammu, India
Keywords: Side Channel Attacks, AES, Caches, Lookup Tables, Spy Process, Victim Process.
Abstract: We design and implement the espionage infrastructure to launch a cache-based side channel attack on AES.
This includes a spy controller and a ring of spy threads with associated analytic capabilities – all hosted on a
single server. By causing the victim process (which repeatedly performs AES encryptions) to be interrupted,
the spy threads capture the victim’s footprints in the cache memory where the lookup tables reside.
Preliminary results indicate that our setup can deduce the encryption key in fewer than 30 encryptions and
with far fewer victim interruptions compared to previous work. Moreover, this approach can be easily
adapted to work on diverse hardware/OS platforms and on different versions of OpenSSL.
1 INTRODUCTION
Through much of the history of cryptography,
attacks on cryptographic algorithms have focused on
cracking hard mathematical problems such as the
factorization of very large integers (which are the
product of two very large primes) and the discrete
logarithm problem (Menezes et al., 1996). More
recently, however, side channel attacks have gained
prominence. These attacks leak sensitive
information through physical channels such as
power, timing, etc. and, typically, are specific to the
actual implementation of the algorithm (Brumley
and Boneh, 2005). An important class of timing
attacks are those based on obtaining measurements
from cache memory systems.
The Advanced Encryption Standard (AES)
(Daemen and Rijmen, 2002) a relatively new
algorithm for secret key cryptography, is now
ubiquitously supported on servers, browsers, etc.
Almost all software implementations of AES
including the widely used cryptographic library,
OpenSSL, make extensive use of table lookups in
lieu of time-consuming mathematical field
operations. Cache-based side channel attacks aim to
retrieve the key of a victim performing AES by
exploiting the fact that access times to different
levels of the memory hierarchy are different.
One possible attack scenario involves a victim
process running on behalf of a data storage service
provider who securely stores documents from
multiple clients and furnishes them on request after
due authentication. The same key or set of keys is
used to encrypt documents from different clients
prior to storage. The attacker or spy shares the same
core as the victim. The spy process flushes out all
the cache lines containing the AES tables – these are
used by the victim in encrypting documents prior to
storage. When CPU control returns to the victim, it
brings in some of the evicted line(s). When control
returns back to the spy, it determines which of the
evicted lines were fetched by the victim by
measuring the time to access them. Information on
which lines of cache were accessed by the victim is
critical in deducing the encryption key.
Cache-based side channel attacks belong to one
of three categories. Timing-driven attacks measure
the time to complete an encryption. Trace-driven
attacks make use of when and in what order specific
lines of cache are accessed in the course of an
encryption. Finally, access-driven attacks need
information only about which lines of cache have
been accessed, not the precise order. Two of the
most successful access-driven attacks (Tromer et al.,
2010), (Gullasch et al., 2011) assume that the victim
and spy are co-located on the same core.
Tromer et al., (2010) assume that the spy is able
to monitor the state of the cache containing the AES
tables after each encryption performed by the victim.
However, this may not always be practically
441
Roy B., Prakash Giri R., C. A. and Menezes B..
Design and Implementation of an Espionage Network for Cache-based Side Channel Attacks on AES.
DOI: 10.5220/0005576804410447
In Proceedings of the 12th International Conference on Security and Cryptography (SECRYPT-2015), pages 441-447
ISBN: 978-989-758-117-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

feasible. Moreover, several hundred encryptions are
required to compute the complete AES key.
Gullasch et al., (2011) use hundreds of spy threads
to monitor the cache. The completely fair (process)
scheduler (CFS) in Linux guarantees that each spy
thread and the victim process get the same aggregate
CPU time in steady state. Also, the sleep-wakeup
routines of the spy threads are carefully controlled
resulting in preemption of the victim when a
sleeping thread wakes up. This, together with the
scheduler’s “fairness guarantees”, ensures that the
victim is preempted after it makes only a single table
access. Their fine-grained approach requires a neural
network to handle the large number of false
positives. Moreover, the slowdown caused by
frequent interruptions of the victim may arouse
suspicion.
The goal of our work is the design and
implementation of an espionage network with
associated analytic capabilities that retrieve the AES
key using fewer encryptions and also fewer
interruptions to the victim process. We aim for both
simplicity and versatility. Earlier attacks may work
on only specific OS versions or with specific
versions of OpenSSL. Further, hardware prefetching
(Hennessy and Patterson, 2012) (implemented on
many modern processors) may render those attacks
unsuccessful. To the extent possible, we seek to
demonstrate successful attacks on diverse computing
platforms and with different OpenSSL versions.
This paper is organized as follows: Section 2
summarizes related work. Section 3 contains a brief
introduction to AES implementation using lookup
tables and the cryptanalytic aspects of the attack. In
Section 4 we present the design and implementation
of our espionage network. A preliminary analysis of
the success of our approach is presented in Section 5
while Section 6 concludes the paper.
2 RELATED WORK
Software implementations of AES based on lookup
tables were first exploited by Bernstein (2005). They
report the extraction of a complete AES key by
exploiting the timing dependencies of encryptions
caused by cache on a Pentium-III machine.
Although their attack is generic and portable, it
needs 2
.
encryptions and sample timing
measurements with known key in an identical
configuration of target server.
Tsunoo et al., (2003) demonstrated a timing-
driven cache attack on DES. They focused on
overall hit ratio during encryption and performed the
attack by exploiting the correlation between cache
hits and encryption time. A similar approach was
used by Bonneau and Mironov (2006) where they
emphasized individual cache collisions during
encryption instead of overall hit ratio. Although the
attack by Bonneau et al. was a considerable
improvement over previous work by Tsunoo et al.
(2003), it still requires 2
timing samples.
Osvik et al., (2006) proposed an access-driven
cache attack where they introduced the Prime and
Probe technique. In the Prime phase, the attacker
fills cache with its own data before encryption
begins. During encryption, the victim evicts some of
the attacker's data from cache in order to load
lookup table entries. In the Probe phase, the attacker
calculates reloading time of its data and finds cache
misses corresponding to those lines where the victim
loaded lookup table entries. In the synchronous
version of their attack, 300 encryptions were
required to recover the 128 bit AES key on
Athlon64 system and in the asynchronous attack,
45.7 bits of information about the key were
effectively retrieved.
The ability to detect whether a cache line has
been evicted or not was further exploited by Neve
and Seifert (2007). They designed an improved
access-driven cache attack on the last round of AES
on single-threaded processors. However the
practicality of their attack was not clear due to
insufficient system and OS kernel version details.
Gullasch et al., (2011) proposed an efficient
access driven cache attack when attacker and victim
use a shared crypto library. The spy process first
flushes the AES lookup tables from all levels of
cache and interrupts the victim process after
allowing it a single lookup table access. After every
interrupt, it calculates the reload time to find which
memory line is accessed by the victim. This
information is further processed using a neural
network to remove noise in order to retrieve the
AES key.
Weiß et al., (2012) used Bernstein's timing attack
on AES running inside an ARM Cortex-A8 single
core system in a virtualized environment to extract
the AES encryption key. Irazoqui, Inci, Eisenbarth
and Sunar (2014a) performed Bernstein's cache
based timing attack in a virtualized environment to
recover the AES secret key from co-resident VM
with 2
encryptions. Later Irazoqui et al., (2014b)
used a Flush + Reload technique and recovered the
AES secret key with 2
encryptions.
SECRYPT2015-InternationalConferenceonSecurityandCryptography
442

3 PRELIMINARIES
We first summarize the software implementation of
AES and then outline the Two Round Attack used in
this paper.
A. AES Summary
AES is a symmetric key algorithm standardized by
the U.S. National Institute of Standards and
Technology (NIST) in 2001. Its popularity is due to
simplicity in its implementation yet it is resistant to
various attacks including linear and differential
cryptanalysis. The full description of AES cipher is
provided in (Daemen and Rijmen 2002). Here, we
briefly summarize only the relevant aspects of its
software implementation.
AES is a substitution-permutation network. It
supports a key size of 128, 192 or 256 bits and block
size = 128 bits. A round function is repeated a fixed
number of times (10 for key size of 128 bits) to
convert 128 bits of plaintext to 128 bits of
ciphertext. The 16 byte input is expressed as a 4×4
array of bytes. Each round involves four steps –
Byte Substitution, Row Shift, Column Mixing and a
round key operation. The round operations are
defined using algebraic operations over the field
2
. The original 16-byte secret key
,..,
is used to derive 10 different round keys to be used
in the round key operation of each round.
In a software implementation, field operations
are replaced by relatively inexpensive table lookups
thereby speeding encryption and decryption. In the
versions of OpenSSL targeted in this paper, five
tables are employed (each of size 1KB). Only four
table lookups and four XORs are involved in
computing each of the four columns per round. Each
table,
,0 4, is accessed using an 8 bit
index resulting in a 32-bit output.
Given a 16-byte plaintext
,...,
,
encryption proceeds by computing a 16-byte
intermediate state
,...,
at each
round . The initial state
is computed using
Equation 5. The first 9 rounds are computed by
updating the intermediate state using the following
set of equations, for 0,...,8.
,
,
,
←
⨁
⨁
⨁
⨁
(1)
,
,
,
←
⨁
⨁
⨁
⨁
(2)
,
,
,
←
⨁
⨁
⨁
⨁
(3)
,
,
,
←
⨁
⨁
⨁
⨁
(4)
Here
refers to the
column vector of the
1
round key expressed as a 4x4 array.
Finally to compute the last round, equations similar
to the above are used except that table
is used
instead of
,...,
. The output of the last round is
the ciphertext. The change of lookup tables in the
last round (for = 10) is due to the absence of the
Column Mixing step.
B. Attack Overview
The granularity of cache access is a block or line
which is 64 bytes in most of our target machines.
Each entry in a table is 4 bytes, so there are 16
entries in each block. Each table contains 256
entries, so it occupies 16 blocks. The first four bits
of an 8-bit table index identify a line within the table
while the last four bits specify the position of the
entry within the line. Thus the first four bits of a
table index are leaked if the attacker can determine
which line of the cache was accessed.
The access-driven cache timing attack described
by Osvik et al., (2006) assumes that the attacker
provides several blocks of plaintext to be encrypted
by the victim during the course of the attack. It
involves two steps. The First Round Attack exploits
the table indices accessed in the first round which
are simply
⨁
,015
(5)
Thus the first four bits of each of the 16 bytes of the
AES key may be derived from the high-order nibble
of the corresponding plaintext and the corresponding
line number of the AES table.
The Second Round Attack seeks to obtain the
low-order nibble of each byte of the key. These can
be deduced from the set of equations in Table 1
which involve only four accesses – one each from
,
,
and
respectively. These equations are
further used in Section 5.
DesignandImplementationofanEspionageNetworkforCache-basedSideChannelAttacksonAES
443
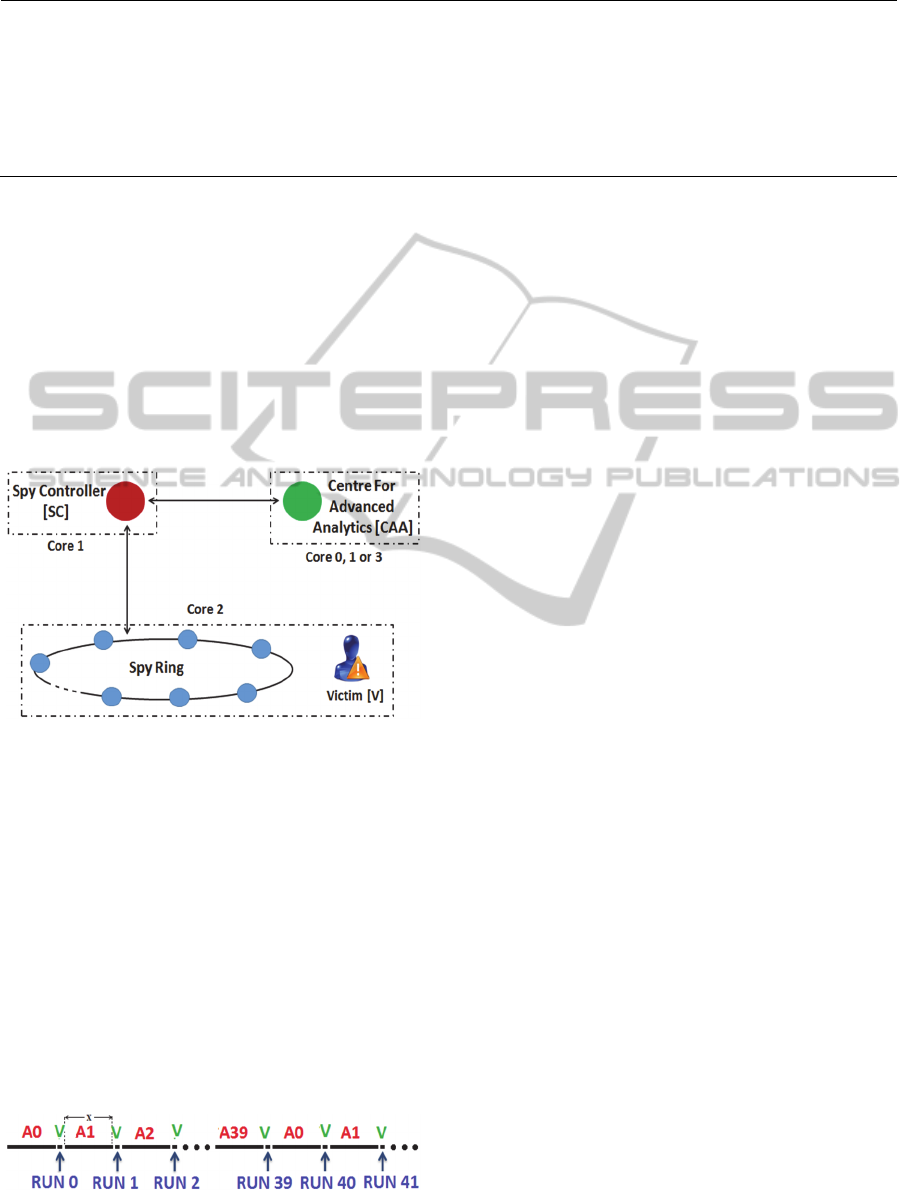
Table 1: Equations used in the Second Round Attack.
⨁
⨁
⨁
⨁ 2 ⦁
⨁
⨁3⦁
⨁
⨁
⨁
(6)
⨁
⨁2⦁
⨁
⨁3⦁
⨁
⨁
⨁
⨁
⨁
⨁
(7)
2⦁
⨁
⨁3⦁
⨁
⨁
⨁
⨁
⨁
⨁
⨁
⨁
⨁
⨁1
(8)
3⦁
⨁
⨁
⨁
⨁
⨁
⨁2⦁
⨁
⨁
⨁
⨁
⨁
⨁
(9)
4 THE ESPIONAGE
INFRASTRUCTURE
Our espionage infrastructure (Figure 1) comprises an
Espionage Network and the Centre for Advanced
Analytics (CAA). The former includes a Spy
Controller (SC) and a Spy Ring. The SC runs on one
CPU core while the ring of spy threads runs on
another core together with the victim.
Figure 1: The Espionage Infrastructure.
Our goal is to cause the execution of spy threads
and the victim (V) to be interleaved as shown in
Figure 2 (in steady state). We refer to an execution
instance of V as a run. During each run, V accesses
the AES tables and the next spy thread that is
scheduled attempts to determine which lines of the
table were accessed in the preceding run of V. The
default time slice (or quantum) assigned by the OS
to a process is large enough to accommodate tens of
thousands of cache accesses. But if V is given this
full time slice it would perform hundreds of
encryptions (each encryption involves 160 table
accesses) thus making it impossible to obtain any
meaningful information about the encryption key.
Figure 2: Execution timeline of spy threads and victim.
The CFS scheduler employed in many Linux
versions uses a calculation based on virtual runtimes
to ensure that the aggregate CPU times allocated to
all processes and threads are nearly equal. In Figure
2, the sum of the CPU times allocated to V is equal
to that of the times given to each of the spy threads.
If the number of threads is and they execute in
round robin fashion, then each run of V is roughly of
duration / where is the uninterrupted time
allocated to any running thread.
The task of a spy thread is to measure the access
times of each of the cache lines containing the AES
tables and then flush the tables from all levels of
cache. It then signals the SC through a shared
boolean variable, finished, that its task is complete.
Finally it waits for an amount of time δ
before
blocking on cond. At this point, all spy threads are in
the blocked state and the OS resumes execution of
V.
Spy Thread (i):
while(true)
wait (cond)
for each cacheLine containing AES
tables
if(accessTime[cacheLine]<THRESHOLD)
isAccessed[cacheLine] = true
clflush(cacheLine)
finished = true
delay loop // time=δ
The SC continuously polls the finished flag. When it
finds that finished has been set, it waits for time δ
and then wakes up the spy thread that has waited the
longest.
Spy Controller :
while (true)
while(finished ≠ true)
delay loop // time=δ
signal(nextThread)
finished = false
Our experiments were performed on Intel(R) Core-
i5 2540M, 2.60GHz processor running Debian Kali
Linux 1.1.0, 64bit, kernel versions 3.14.5 and 3.18
SECRYPT2015-InternationalConferenceonSecurityandCryptography
444
using the C implementation of AES in OpenSSL
0.9.8a. This version of OpenSSL uses a separate
table for the last round of encryption. The core-i5
has 3-level cache architecture. The L1 cache is
32KB (8-way associative), L2 cache is 256KB (8-
way associative) and L3 cache is 3MB (12-way
associative). Each CPU core has private L1 and L2
caches whereas L3 is shared among different CPU
cores.
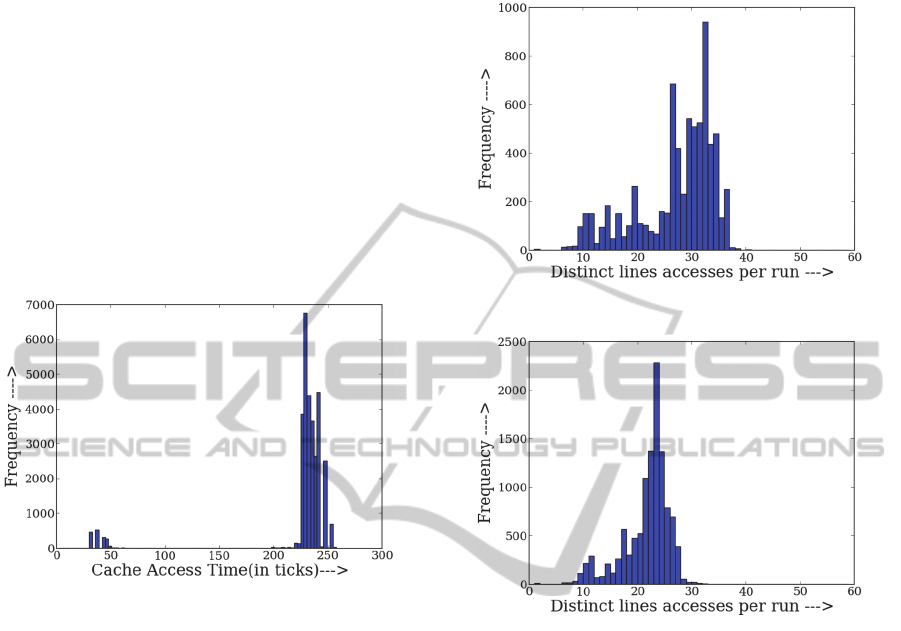
The distribution of cache hit and miss times as
measured by us were clearly separated as shown in
Figure 3 (32 - 68 ticks for a cache hit and 200 – 260
ticks for a cache miss). Based on these
measurements we set the threshold for hit/miss
determination = 100 ticks.
Figure 3: Distribution of cache Hit and Miss Times.
Three design parameters can be tweaked at the
discretion of the SC. These are the number of
threads and the two delay parameters, δ
and δ
. As
the number of threads increases, the execution time
of V during each run decreases and V would make
fewer table accesses. This is indeed the case as
shown in Figures 4 and 5. The number of distinct
accesses per run is concentrated between 28 and 37
with 10 spy threads but the range decreases to 18-27
for the case of 40 spy threads.
The delay at the SC, δ
, was designed to defer
waking a spy thread. This was necessitated by the
fact that occasionally multiple threads would get
executed in sequence without any intervening run of
V. Then, when V got scheduled, it computed several
encryptions and synchronization between the
espionage network and V was lost. Finally, the delay
in the spy thread, δ
, was intended to delay the start
of a run by V and so decrease the number of table
accesses made by V if indeed that was necessary.
The set of accessed lines in each table is
communicated to the CAA. The latter analyzes the
results and derives the AES key. Depending on the
“quality” of input it receives, the CAA may
recommend a change of design parameters to the
SC.
Figure 4: # Accesses per run (# Spy Threads =10).
Figure 5: # Accesses per run (# Spy Threads =40).
In the next section, we perform some back of the
envelope calculations to demonstrate that the AES
key on our set-up can be deduced with results from
fewer than 30 encryptions.
5 ANALYSIS
To retrieve a given AES key, we performed
successive encryptions on random plaintexts with
that key. Experimental results on the setup described
in Section 4 indicate that there are almost always
two consecutive runs containing accesses to
(see
Table 2). Let these be denoted R1 and R2 and let the
run following R2 be R3. The former are useful
synchronization points signaling that an encryption
is complete and a new one has begun (or is about to
begin). If R2 also has accesses to Tables
–
,
then those would certainly include accesses made in
round 1 of the new encryption. Our experimental
results with 40 threads in the Spy Ring show that,
collectively, R2 and R3 access around 7-10 distinct
DesignandImplementationofanEspionageNetworkforCache-basedSideChannelAttacksonAES
445
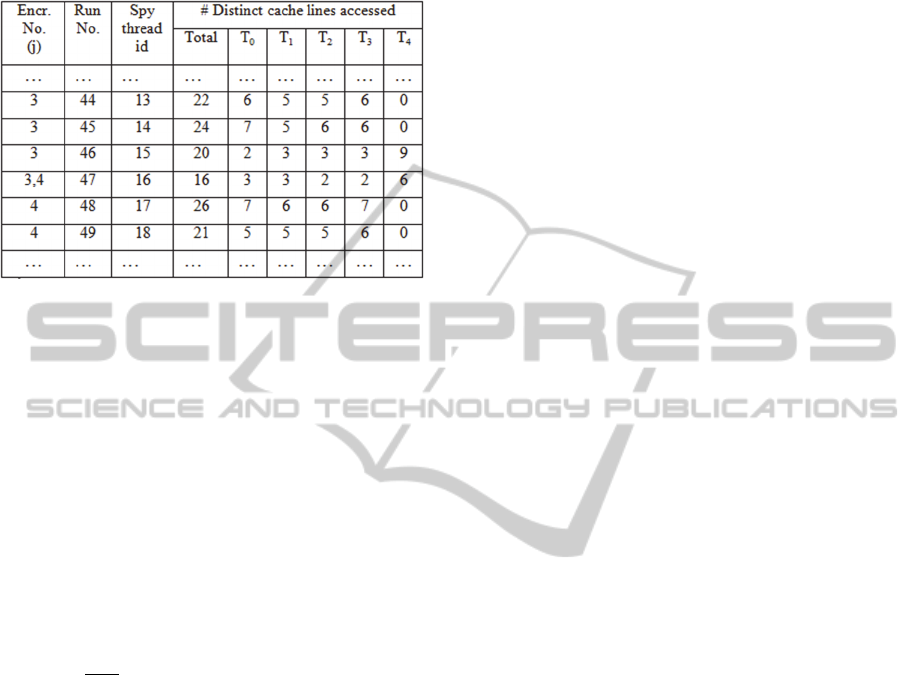
lines in each of
,
,
and
.
Table 2: Sample number of distinct accesses per table in
consecutive runs.
Let
,
denote the subset of distinct line numbers
in Table
accessed in the first two runs of
Encryption . Also, let ̂ denote the high order
nibble of. We next show how to obtain
as part
of the First Round Attack.
We associate a variable,, (initialized to 0)
with each of the 16 possible values of
. For each
encryption,1,2,...,, we compute the possible
values of ⊕
where ∈
,
and increment
by 1 the score of . The with the highest score is
the true value of
. Indeed, given highly accurate
measurements by the spies, the true value of
will
end up with a perfect score of after the
encryptions. On the other hand, the probability that
any other value of gets this score is
only
∏
,
. For
,
~8and 9, this works
out to 2
-9
. In a similar manner, we can obtain the
first nibble of each of the 16 bytes of the AES key.
To obtain the second nibble of each byte of the
AES key, we use the Second Round Attack
(Equations 6-9 in Section 3). Consider the 16-bit
integer, , obtained by concatenating candidate
values for the low-order nibbles of
,
,
and
. Again, we associate a variable, , with
each of the 2
16
possible values of and initialize
these to 0. For an encryption and corresponding
plaintext we do the following. For each possible
value of , we obtain the value of
from Equation
6. We then check to see whether
∈
,
. If so,
we increment by 1 the score associated with . We
repeat this for 20-30 encryptions. The with the
perfect score would reveal the true values of the
low-order nibbles of each of
,
,
and
.
Performing an analysis similar to that for the First
Round Attack leads us to conclude that it is highly
improbable that any other candidate comes close to
the winner. Finally, the rest of the key bits may be
obtained using Equations 7, 8 and 9.
6 CONCLUSIONS
There are two parts of this work. The first part
which is heavily experimental can be summarized
by the following modified lyrics of an evergreen
song (Synchronicity, 1983).
. . .
Every move you make
. . .
Every step you take
. . .
Every single tick
Every line you pick
I’ll be watching you.
We have been able to accurately monitor cache hits
and misses of the AES lookup tables with our
espionage network. We have completed a
preliminary analysis of the results and feel that the
heuristics to be implemented by the CAA (the
second part of this work) will obtain the keys with
around 12 to 30 encryptions. Though we have
completed our experiments on a specific platform,
we will next investigate the success of our attack on
other platforms and other versions of OpenSSL.
REFERENCES
Bernstein, D. J. (2005). Cache-timing attacks on aes.
Bonneau, J. and Mironov, I. (2006). Cache-collision
timing attacks against aes. In Cryptographic
Hardware and Embedded Systems-CHES 2006, pages
201–215. Springer.
Brumley, D. and Boneh, D. (2005). Remote timing attacks
are practical. Computer Networks, 48(5):701–716.
Daemen, J. and Rijmen, V. (2002). The design of
Rijndael: AES-the advanced encryption standard.
Springer Science & Business Media.
Gullasch, D., Bangerter, E., and Krenn, S. (2011). Cache
games–bringing access-based cache attacks on aes to
practice. In Security and Privacy (SP), 2011 IEEE
Symposium on, pages 490–505. IEEE.
Hennessy, J. L. and Patterson, D. A. (2012). Computer
architecture: a quantitative approach. Elsevier.
Irazoqui, G., Inci, M. S., Eisenbarth, T., and Sunar, B.
(2014a). Fine grain cross-vm attacks on xen and
vmware. In Big Data and Cloud Computing
(BdCloud), 2014 IEEE Fourth International
Conference on, pages 737–744. IEEE.
Irazoqui, G., Inci, M. S., Eisenbarth, T., and Sunar, B.
SECRYPT2015-InternationalConferenceonSecurityandCryptography
446

(2014b). Wait a minute! a fast, cross-vm attack on aes.
In Research in Attacks, Intrusions and Defenses, pages
299–319. Springer.
Menezes, A. J., Van Oorschot, P. C., and Vanstone, S. A.
(1996). Handbook of applied cryptography. CRC
press
Neve, M. and Seifert, J.-P. (2007). Advances on
accessdriven cache attacks on aes. In Selected Areas in
Cryptography, pages 147–162. Springer.
Osvik, D. A., Shamir, A., and Tromer, E. (2006). Cache
attacks and countermeasures: the case of aes. In Topics
in Cryptology–CT-RSA 2006, pages 1–20. Springer.
Synchronicity, (1983)
http://www.songfacts.com/detail.php?id=548.
Tromer, E., Osvik, D. A., and Shamir, A. (2010). Efficient
cache attacks on aes, and countermeasures. Journal of
Cryptology, 23(1):37–71.
Tsunoo, Y., Saito, T., Suzaki, T., Shigeri, M., and
Miyauchi, H. (2003). Cryptanalysis of des
implemented on computers with cache. In
Cryptographic Hardware and Embedded Systems-
CHES 2003, pages 62–76. Springer.
Weiss, M., Heinz, B., and Stumpf, F. (2012). A cache
timing attack on aes in virtualization environments. In
Financial Cryptography and Data Security, pages
314–328. Springer.
DesignandImplementationofanEspionageNetworkforCache-basedSideChannelAttacksonAES
447
