
Practical and Secure Integrated PKE+PEKS with Keyword Privacy
Francesco Buccafurri
1
, Gianluca Lax
1
, Rajeev Anand Sahu
2
and Vishal Saraswat
2
1
DIIES Department, University of Reggio Calabria, Reggio Calabria, Italy
2
C.R.Rao Advanced Institute of Mathematics Statistics and Computer Science, Hyderabad, India
Keywords:
PKE+PEKS, Searchable Encryption, Perfect Keyword Privacy, Asymmetric Pairings (Type 3), Provable
Security, Standard Model, SXDH, E-governance, Privacy in the Cloud.
Abstract:
Public-key encryption with keyword search (PEKS) schemes are useful to delegate searching capabilities on
encrypted data to a third party, who does not hold the entire secret key, but only an appropriate token which
allows searching operations but preserves data privacy. We propose an efficient and practical integrated public-
key encryption (PKE) and public-key encryption with keyword search (PEKS) scheme (PKE+PEKS) which
we prove to be secure in the strongest security notion for PKE+PEKS schemes. In particular, we provide
a unified security proof of its joint CCA-security in standard model. The security of our scheme relies on
Symmetric eXternal Diffie-Hellman (SXDH) assumption which is a much simpler and more standard hardness
assumption than the ones used in most of the comparable schemes. Ours is the first construction to use
asymmetric pairings which enable an extremely fast implementation useful for practical applications. Finally
we compare our scheme with other proposed integrated PKE+PEKS schemes and provide a relative analysis
of its efficiency.
1 INTRODUCTION
(Boneh et al., 2004) gave the first formal construction
of “searchable encryption” in public key setting and
called it public key encryption with keyword search
(PEKS), popularly known as BDOP scheme. The ba-
sic advantage of this primitive is that it allows one
to delegate to a third party the capability of “search-
ing on public key encrypted data” without impact-
ing privacy. PEKS basically enables a search func-
tion to a public key encryption (PKE) scheme and
hence a PEKS is directly related to an underlying
PKE scheme and both are used together. We call
such a combination integrated PKE and PEKS and
denote it as PKE+PEKS. For a PKE+PEKS scheme
the privacy must be simultaneously achieved for both
the message (that is, data) and the keyword, that is,
IND-PKE-CCA and IND-PEKS-CCA. But achieving
the security based on two independent CCA-secure
schemes is not trivial. So a unified security model for
the joint CCA-security of PKE+PEKS is desired.
1.1 Related Work
(Abdalla et al., 2005) defined computational, sta-
tistical and perfect variations of consistency for a
PEKS scheme and proposed a transform of an anony-
mous identity-based encryption (IBE) scheme to a
PEKS scheme. (Baek et al., 2006) formally de-
fined a combined scheme for PKE and PEKS based
on the BDOP-PEKS and a variation of ElGamal en-
cryption scheme with the randomness reuse tech-
nique (Kurosawa, 2002). (Crescenzo and Saraswat,
2007) constructed a PEKS scheme which, unlike all
other schemes, is not based on bilinear forms. Vari-
ous groups (Boyen and Waters, 2006; Fuhr and Pail-
lier, 2007; Zhang and Imai, 2007; Baek et al., 2008;
Abdalla et al., 2010) have studied the design and effi-
ciency of the PEKS schemes while (Lu et al., 2009;
Shmueli et al., 2010; Ibraimi et al., 2011) have studied
the application aspects of PEKS.
(Boneh et al., 2004) formalized the security pre-
cisely for the PEKS scheme with IND-PEKS-CPA
notion. (Baek et al., 2008) combined PKE and PEKS
with a joint security notion but their notion cov-
ered only data privacy and not the keyword privacy.
(Zhang and Imai, 2007) first extended the security no-
tion to achieveboth data privacy and keywordprivacy.
The security notion for data security is IND-PKE-
CCA, which is achieved in their scheme using a tag-
based CCA-secure PKE scheme, and for keyword
privacy the notion is IND-PEKS-CPA, which they
448
Buccafurri F., Lax G., Sahu R. and Saraswat V..
Practical and Secure Integrated PKE+PEKS with Keyword Privacy.
DOI: 10.5220/0005577104480453
In Proceedings of the 12th International Conference on Security and Cryptography (SECRYPT-2015), pages 448-453
ISBN: 978-989-758-117-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

have achieved using a CPA-secure PEKS scheme.
But their construction suffers from double key size,
which increases key-maintenance overheads unnec-
essarily during the practical implementations. But
none of the above works prove joint security of a
PKE+PEKS scheme in strongest notion, that is, ‘IND-
PKE+PEKS-CCA security’. (Abdalla et al., 2010) in-
troduced a new combined CCA-security notion on the
standard model with a privilege to the adversary to ac-
cess both decryption oracle and test oracle. Following
the idea of (Dodis and Katz, 2005), they constructed
a PKE+PEKS scheme by combining two schemes, a
tag-based CCA-secure PKE scheme and a tag-based
CCA-secure PEKS scheme. But their construction
suffers from double key size and an increase in the
computational overhead of the resulting PKE+PEKS.
Recently, (Chen et al., 2014) gave a generic construc-
tion of a PKE+PEKS scheme from an anonymous
IBE and one-time signatures using a single key for
both PKE and PEKS operations.
1.2 Our Contribution
As discussed above that a PEKS scheme joins PKE
to provide it a searchable functionality, hence com-
bining both the schemes in a secure manner is of
great interest. Attempts for the security of PEKS
were started with the IND-PEKS-CPA notion of secu-
rity on random oracle (Boneh et al., 2004), where the
‘keyword’ is considered as a plaintext. Though there
have been lot of research on searchable encryption,
the only fully secure schemes (Abdalla et al., 2010;
Chen et al., 2014) are too inefficient to be practical
enough to be used in implementation. We propose a
state of art efficient, computationally and bandwidth-
wise, fully secure practical scheme which, we believe,
can be used in real applications.
At the heart of our scheme are asymmetric pair-
ings (Type 3) which enables our scheme to have
very short ciphertexts and extremely fast implemen-
tation. Typically, compared with symmetric pairings,
for Type 3 pairings, the estimated bit sizes of group el-
ements, over which most of the computation is done
and are communicated, are four times smaller for 256-
bit (AES) security (Chen et al., 2012).
We also give a relatively unified model for the
joint security of PKE+PEKS scheme. We note that
a scheme with a security proof in the random oracle
model implies no security in the real world (Canetti
et al., 2004), security of our scheme is proved in
the standard model and hence our scheme achieves
practical security. We will provide a full security anal-
ysis and will envisage a few suitable applications in
the full version of this paper.
2 PRELIMINARIES
We denote by y ← A(x) the operation of running a ran-
domized or deterministic algorithm A(x) and storing
the output to the variable y. If X is a set, then v
$
← X
denotes the operation of choosing an element v of X
according to the uniform random distribution on X.
We say that a given function f : N → [0, 1] is negli-
gible in n if f(n) < 1/p(n) for any polynomial p for
sufficiently large n. For a group G and g ∈ G, we write
G = hgi if g is a generator of G. We let G
1
, G
2
and
G
T
be multiplicative cyclic groups of the same prime
order q and e : G
1
× G
2
→ G
T
be a pairing defined as
follows.
Definition 1. A map e : G
1
× G
2
→ G
T
is called a
cryptographic bilinear map or a pairing if it satisfies
the following properties:
1. Bilinearity: For all (g
1
,g
2
) ∈ G
1
× G
2
and for all
a,b ∈ Z
q
, e(g
a
1
,g
b
2
) = e(g
1
,g
2
)
ab
,
2. Non-Degeneracy: There exists (g
1
,g
2
) ∈ G
1
× G
2
such that e(g
1
,g
2
) 6= 1, the identity of G
T
.
3. Computability: There exists an efficient algorithm
to compute e(g
1
,g
2
) ∈ G
T
, for all (g
1
,g
2
) ∈ G
1
×
G
2
.
A pairing e : G
1
× G
2
→ G
T
is called a symmetric
or a Type-1 pairing if G
1
= G
2
otherwise it is called
asymmetric. Asymmetric pairings are further catego-
rized into Type 2 and Type 3 pairings. If there exists
an efficiently computable isomorphism between G
1
and G
2
, the pairing is referred to as Type 2, whereas
if there is no efficiently computable isomorphism be-
tween G
1
and G
2
, the pairing is referred to as Type-3.
2.1 Dual Pairing Vector Space
Let g ∈ G and (g
1
,g
2
) ∈ G
1
× G
2
. For a vector
v = (v
1
,... ,v
n
) ∈ Z
n
q
we define a vector of group
elements as g
v
:= (g
v
1
,... ,g
v
n
). For vectors v =
(v
1
,... ,v
n
),w = (w
1
,... ,w
n
) ∈ Z
n
q
and for any a ∈ Z
q
,
we further define the following properties on such a
vector space,
(g
a
)
v
:= g
av
= (g
av
1
,... ,g
av
n
);
g
v
g
w
:= g
v+w
= (g
v
1
+w
1
,... ,g
v
n
+w
n
)
e(g
v
1
,g
w
2
) :=
n
∏
i=1
e(g
v
i
1
,g
w
i
2
) = e(g
1
,g
2
)
v·w
.
Definition 2. Two bases D := {d
1
,d
2
,d
3
,d
4
} and
D
∗
= {d
∗
1
,d
∗
2
,d
∗
3
,d
∗
4
} of Z
4
q
are dual orthonormal if
for all 1 ≤ j 6= k ≤ 4,
d
j
· d
∗
k
= 0 (mod q) and d
j
· d
∗
j
= ψ (mod q)
where ψ
$
← Z
q
.
PracticalandSecureIntegratedPKE+PEKSwithKeywordPrivacy
449

For such dual bases, for all (g
1
,g
2
) ∈ G
1
× G
2
,
e(g
d
j
1
,g
d
∗
k
2
) = 1 whenever j 6= k.
Theorem 1 ((Okamoto and Takashima, 2010)). We
can efficiently select two random dual orthonormal
bases D := {d
1
,d
2
,d
3
,d
4
} and D
∗
= {d
∗
1
,d
∗
2
,d
∗
3
,d
∗
4
}
of Z
4
q
.
2.2 Symmetric eXternal Diffie-Hellman
(SXDH) Assumption
Let G
1
and G
2
be multiplicative cyclic groups as
stated above, with g
1
∈ G
1
and g
2
∈ G
2
.
Definition 3. Let G be a multiplicative cyclic group
and g a generator. Let a,b,c ∈ Z
∗
q
be randomly chosen
and kept secret. Given g, g
a
,g
b
,g
c
∈ G, the decisional
Diffie-Hellman problem (DDHP) in the group G is to
decide if g
ab
= g
c
.
Definition 4. The DDH assumption holds in a group
G if there is no efficient algorithm which can solve
DDHP in G.
Definition 5. Given two cyclic groups G
1
and G
2
, we
say the Symmetric eXternal Diffie-Hellman (SXDH)
assumption holds if DDH assumption is true in both
the groups G
1
and G
2
.
3 INTEGRATED PKE AND PEKS
SCHEME (PKE+PEKS)
Here we give a formal definition of an integrated
public-key encryption (PKE) and public-key en-
cryption with keyword search (PEKS) scheme
(PKE+PEKS) based on the works of (Boneh et al.,
2004; Baek et al., 2008; Chen et al., 2014).
In PEKS, three parties called sender, receiver and
server are involved. The sender is a party that creates
and sends encrypted keywords, which we call PEKS
ciphertexts. The server is a party that receives PEKS
ciphertexts and performs search upon receiving trap-
doors from the receiver. The receiver is a party that
creates trapdoors and sends them to the server to find
the data that it wants.
3.1 Formal Definition of PKE+PEKS
A PKE+PEKS scheme comprises of six algorithms:
Setup, KeyGen, Encrypt, Decrypt, TokenGen and Test.
G ← Setup(1
k
): This is the system initialization al-
gorithm run by the receiver which takes as input a
security parameter 1
k
and outputs public parameters
Params G := (q, G
1
,G
2
,G
T
,g
1
,g
2
,e) where G
1
=
hg
1
i, G
2
= hg
2
i and G
T
are cyclic groups of prime
order q, and e : G
1
× G
2
→ G
T
is a Type 3 pairing.
(pk
X
,sk
X
) ← KeyGen(G): This is the key genera-
tion algorithm run by a user X which takes as in-
put the public parameters G and outputs a key pair
(pk
X
,sk
X
). For the receiver X = R, the key pair is
its (public key, private key) pair (pk
R
,sk
R
) and for
a sender X = S, the key pair is its (verification key,
signing key) pair (vk
S
,sk
S
).
U ← Encrypt(G, pk
R
,sk
S
,m,w): This is a random-
ized algorithm run by the sender and takes input
Params G, the receiver’s public key pk
R
, the sender’s
signing key sk
S
, a message m and keyword w and
outputs the joint PKE+PEKS ciphertext U.
m ← Decrypt(G, pk
R
,sk
R
,U) This is a determinis-
tic algorithm run by the receiver and takes input
Params G, the receiver’s public key pk
R
and the se-
cret key sk
R
and a ciphertext U and outputs a mes-
sage m or ⊥.
t
w
← TokenGen(G, pk
R
,sk
R
,w) This is a random-
ized algorithm run by the receiver and takes input
Params G, the receiver’s public key pk
R
and the se-
cret key sk
R
and a keyword w and outputs a token t
w
which it gives to the server.
b ← Test(G, pk
R
,t
w
,U) This is a deterministic algo-
rithm run by the server and takes input Params G, the
receiver’s public key pk
R
, a token t
w
and a ciphertext
U and outputs a bit b ∈ {0,1} or ⊥.
Where the context is clear, the inputs Params and
the keys will be assumed to be implicit and we will
not write them explicitly in the algorithms.
3.2 Security Model for PKE+PEKS
Joint Data and Keyword Privacy for PKE+PEKS
schemes is defined via the following experiment.
Setup: On input a security parameter 1
k
, the chal-
lenger C runs KeyGen(1
k
) to generate the public pa-
rameter Params G and the system key pair (pk,sk)
and gives the adversary A the public key pk.
Phase 1: A can adaptively make three types of
queries:
• Decryption query hui: C responds with m ←
Decrypt(sk,u).
• Token query hwi: C responds with t
w
←
TokenGen(sk,w).
• Test query hu, wi: C responds with Test(u,t
w
)
where t
w
← TokenGen(sk, w).
Challenge: A outputs two messages m
∗
0
and m
∗
1
and
two keywords w
∗
0
and w
∗
1
. C picks two random bits
a,b and sends u
∗
← Encrypt(pk,m
∗
a
,w
∗
b
) to A as the
challenge ciphertext.
Phase 2: A can adaptively make more queries as in
Phase 1 subject to the restrictions that it is not al-
SECRYPT2015-InternationalConferenceonSecurityandCryptography
450

lowed to make
• Decryption query hu
∗
i,
• Token queries hw
∗
0
i and hw
∗
1
i, and
• Test queries hu
∗
,w
∗
0
i and hu
∗
,w
∗
1
i.
C responds the same way as in Phase 1.
Guess: A outputs its guess (a
0
,b
0
) for (a,b).
Definition 6 (Data Privacy). The adversary succeeds
in breaking the data privacy if a
0
= a and we say that
a PKE+PEKS scheme has data privacy if there is no
PPT adversary with a non-negligible advantage in 1
k
in the above experiment.
Definition 7 (Keyword Privacy). The adversary suc-
ceeds in breaking the keyword privacy if b
0
= b
and we say that a PKE+PEKS scheme has keyword
privacy if there is no PPT adversary with a non-
negligible advantage in 1
k
in the above experiment.
Definition 8. We say a PKE+PEKS scheme is jointly
CCA-secure if it has keyword privacy and data
privacy simultaneously.
Remark 1. The joint CCA-security notion defined
by us embodies both IND-PKE-CCA security and
IND-PEKS-CCA security for PKE+PEKS in the joint
sense and is stronger than previous ones considered
in (Baek et al., 2006; Zhang and Imai, 2007), both of
which are insecure in our joint CCA-security notion
as analyzed in Section 1.
4 PROPOSED SCHEME
We present here our efficient and CCA secure
integrated PKE+PEKS scheme motivated by the short
IBE and IBS schemes of (Chen et al., 2012). As de-
scribed in Section 3, our scheme consists of the fol-
lowing algorithms: Setup, KeyGen, Encrypt, Decrypt,
TokenGen, and Test.
Setup: A receiver R wishing to receive
joint PKE+PEKS messages generates G :=
(q,G
1
,G
2
,G
T
,g
1
,g
2
,e) where G
1
= hg
1
i, G
2
= hg
2
i
and G
T
are cyclic groups of prime order q and
e : G
1
× G
2
→ G
T
is a Type 3 pairing. The receiver
then chooses two cryptographic hash functions
H : {0,1}
∗
→ Z
q
and J : {0, 1}
∗
→ G
T
. Finally, R
publishes G, H and J as the public parameters of the
system. (These may be considered as part R’s public
key, but for sake of clarity we keep these separate.)
KeyGen: To generate keys for the system, the re-
ceiver does the following:
• samples random dual orthonormal bases D
and D
∗
where D = {d
1
,d
2
,d
3
,d
4
} and D
∗
=
{d
∗
1
,d
∗
2
,d
∗
3
,d
∗
4
} so that for all 1 ≤ j ≤ 4, d
j
·d
∗
j
= ψ;
• picks α
$
← Z
q
;
• computes g
α
T
:= e(g
1
,g
2
)
αd
1
·d
∗
1
;
• sets the public key pk
R
= {g
α
T
,g
d
1
1
,g
d
2
1
}; and
• sets the master secret sk
R
= {α,g
d
∗
1
2
,g
d
∗
2
2
}.
Encrypt: To encrypt a message m ∈ G
T
with a
keyword w ∈ {0,1}
∗
for the receiver R, a sender S
does the following:
• samples random dual orthonormal bases E and E
∗
where E = {e
1
,e
2
,e
3
,e
4
} and E
∗
= {e
∗
1
,e
∗
2
,e
∗
3
,e
∗
4
}
so that for all 1 ≤ j ≤ 4, e
j
· e
∗
j
= φ;
• picks β
$
← Z
q
;
• computes g
β
T
:= e(g
1
,g
2
)
βe
1
·e
∗
1
;
• sets the signing key sk
S
= (β,g
e
∗
1
2
,g
e
∗
2
2
); and
• sets the verification key vk
S
= (g
β
T
,g
e
1
1
,g
e
2
1
).
• sets vk = J(vk
S
), picks x,y
$
← Z
q
and computes
• ID
vk
= H(0kvk) and ID
w
= H(1kw)
• C
m
= (C
m
1
:= m· (g
α
T
)
x
,C
m
2
:= g
x(d
1
+ID
vk
d
2
)
1
)
• C
w
= (C
w
1
:= vk· (g
α
T
)
x
,C
w
2
:= g
x(d
1
+ID
w
d
2
)
1
)
• t = H(C
m
kC
w
)
• σ = g
(β+yt)e
∗
1
−ye
∗
2
1
and finally declares the ciphertext U =
(vk
S
,C
m
,C
w
,σ).
Decrypt: To decrypt the ciphertext U =
(u
1
,u
2
,u
3
,u
4
), the receiver does the following:
• obtains h
1
, h
2
and h
T
from u
1
;
• computes t = H(u
2
ku
3
); and
• checks whether e(u
4
,g
e
1
+te
2
2
) = g
β
T
.
• If the above equality does not hold then outputs ⊥.
Otherwise it obtains C
1
,C
2
from u
2
and
• computes vk = J(u
1
) and sets ID
vk
= H(0kvk);
• computes the corresponding decryption key
SK
ID
vk
= g
αd
∗
1
+(ID
vk
·d
∗
1
−d
∗
2
)
2
;
• Finally it outputs m ←
C
1
e(C
2
,SK
ID
vk
)
.
TokenGen: To generate a token t
w
for the keyword
w, the receiver
• computes ID
w
= H(1kw);
• picks r
$
← Z
q
and computes t
w
= g
αd
∗
1
+r(ID
w
·d
∗
1
−d
∗
2
)
2
and gives to the server t
w
.
Test: To test whether the ciphertext U =
(u
1
,u
2
,u
3
,u
4
) includes the keyword w or not
using the token t
w
, the server does the following:
• obtains h
1
, h
2
and h
T
from u
1
;
• computes t = H(u
2
ku
3
); and
• checks whether e(u
4
,g
e
1
+te
2
2
) = g
β
T
.
PracticalandSecureIntegratedPKE+PEKSwithKeywordPrivacy
451

• If the above equality does not hold then outputs 0.
• Otherwise it obtains C
3
,C
4
from u
3
and checks
whether
C
3
e(C
4
,t
w
)
= J(u
1
)
• If yes then outputs 1, else outputs 0.
4.1 Correctness of the Proposed Scheme
Theorem 2. The presented scheme is correct.
Proof. The decryption is correct since
e(C
2
,SK
ID
vk
) = e(g
x(d
1
+ID
vk
d
2
)
1
,g
αd
∗
1
+r(ID
vk
d
∗
1
−d
∗
2
)
2
)
= e(g
1
,g
2
)
αxd
1
·d
∗
1
e(g
1
,g
2
)
xrID
vk
(d
1
·d
∗
1
−d
2
·d
∗
2
)
= g
αx
T
and
C
1
e(C
2
,SK
ID
vk
)
=
m· (g
α
T
)
x
g
αx
T
= m.
The testing is correct since
e(C
4
,t
w
) = e(g
x(d
1
+ID
w
d
2
)
1
,g
αd
∗
1
+r(ID
w
·d
∗
1
−d
∗
2
)
2
)
= e(g
1
,g
2
)
x(d
1
+ID
w
d
2
)(αd
∗
1
+r(ID
w
·d
∗
1
−d
∗
2
))
= e(g
1
,g
2
)
x(α+rID
w
)(d
1
·d
∗
1
+ID
w
d
2
·d
∗
1
)−xID
w
(d
1
·d
∗
2
−d
2
·d
∗
2
)
= e(g
1
,g
2
)
x(α+rID
w
)ψ−xID
w
ψ
= e(g
1
,g
2
)
xαψ
= g
xα
T
and
C
3
e(C
4
,t
w
)
=
vk· (g
α
T
)
x
g
xα
T
= vk = J(u
1
).
5 SECURITY ANALYSIS
In this section, we analyze the security of our scheme.
We here give a proof sketch of the security of our
scheme. Note that the generic proof is quite compli-
cated and causes security degradation and in the full
version of this paper we will give a direct proof which
is conceptually simpler and provides tight bounds.
Note that the basic IBE scheme that we use in
our scheme was proved to be ANO-IBE-CCA anony-
mous (Chen et al., 2012) based on the SXDH as-
sumption. The signature scheme that we use is a
modification of the signature scheme in (Chen et al.,
2012) which was obtained using a Naor-transform
of the IBE in (Chen et al., 2012) and is proved
to be sEUF-CMA secure based on the SXDH as-
sumption. Straight-forward modifications of proof
in (Chen et al., 2012) will also show the security
of our signature scheme under the same assumption.
Thus proceeding as in (Chen et al., 2014), we can also
prove that our scheme is jointly CCA-secure, that is,
our scheme is both IND-PKE-CCA and IND-PEKS-
CCA and has keyword privacy and data privacy si-
multaneously.
6 EFFICIENCY ANALYSIS
We compare the efficiency of our Integrated
PKE+PEKS scheme with the existing PEKS
schemes (Baek et al., 2006; Zhang and Imai, 2007;
Chen et al., 2014) in Table 1, and show that our
scheme is more efficient than these schemes. In
each of the four phases: Encryption, Decryption,
Token Gen. and Test, we compare the total number
of bilinear pairings (P), exponentiations and inverse
in Z
q
denoted as E(Z
q
) and I(Z
q
), exponentiations
and multiplications in G
1
denoted as E(G
1
) and
M(G
1
), exponentiations and multiplications in G
2
denoted as E(G
2
) and M(G
2
) and exponentiations
and multiplications in G
T
denoted as E(G
T
) and
M(G
T
). Our scheme uses asymmetric pairings so we
have considered operations in all the three different
groups, G
1
, G
2
and G
T
, while for schemes using
symmetric pairings, we have counted operations in
groups G
1
and G
2
, considering |G
2
| ≈ |G
T
|.
7 CONCLUSION AND FUTURE
WORK
We have proposed an integrated public-key en-
cryption (PKE) and public-key encryption with
keyword search (PEKS) scheme (PKE+PEKS) which
is efficient, computationally and bandwidth-wise,
and secure in the strongest sense for PKE+PEKS
schemes. In the full version of this paper, we will
provide a full security analysis of our scheme in
a relatively unified model for the joint security of
PKE+PEKS scheme in standard model. Further, we
will provide a more detailed efficiency analysis and
comparison with existing similar schemes. Finally we
will envisage a few suitable applications for practical
implementation of our scheme.
ACKNOWLEDGEMENT
This work has been partially supported by the
TENACE PRIN Project (n. 20103P34XC) funded by
the Italian Ministry of Education, University and Re-
search, and by the Program “Programma Operativo
SECRYPT2015-InternationalConferenceonSecurityandCryptography
452
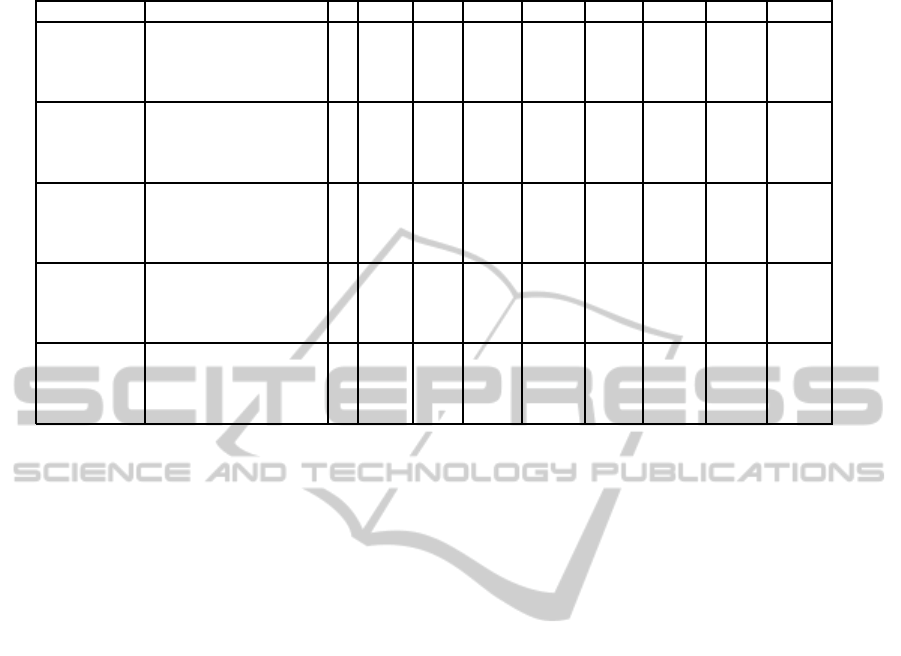
Table 1: Efficiency Comparison.
Operation Scheme P E(Z
q
) I(Z
q
) E(G
1
) M(G
1
) E(G
2
) M(G
2
) E(G
T
) M(G
T
)
Encryption
(Baek et al., 2006) 1 0 0 2 0 - - 1 0
(Zhang and Imai, 2007) 2 0 0 2 1 - - 6 1
(Chen et al., 2014) 5 0 1 7 2 - - 5 2
Our scheme 0 0 0 2 0 1 0 1 2
Decryption
(Baek et al., 2006) 0 0 0 1 0 - - 0 0
(Zhang and Imai, 2007) 0 0 0 0 0 - - 2 1
(Chen et al., 2014) 3 0 1 3 2 - - 0 1
Our scheme 2 0 0 1 0 0 0 0 1
TokenGen
(Baek et al., 2006) 0 0 0 1 0 - - 0 0
(Zhang and Imai, 2007) 0 0 0 1 1 - - 0 0
(Chen et al., 2014) 0 0 1 1 1 - - 0 0
Our scheme 0 0 0 0 0 0 0 0 0
Test
(Baek et al., 2006) 1 0 0 0 0 - - 0 0
(Zhang and Imai, 2007) 1 0 0 0 0 - - 1 1
(Chen et al., 2014) 4 1 0 2 2 0 0 2 3
Our scheme 2 0 0 1 0 0 0 1 0
Overall
comparison
(Baek et al., 2006) 2 0 0 4 1 - - 1 0
(Zhang and Imai, 2007) 3 0 0 3 2 - - 9 3
(Chen et al., 2014) 12 1 3 13 7 - - 7 6
Our scheme 4 0 0 4 0 1 0 2 3
Nazionale Ricerca e Competitivit`a” 2007-2013, Dis-
tretto Tecnologico CyberSecurity funded by the Ital-
ian Ministry of Education, University and Research.
REFERENCES
Abdalla, M., Bellare, M., Catalano, D., Kiltz, E., Kohno, T.,
Lange, T., Malone-Lee, J., Neven, G., Paillier, P., and
Shi, H. (2005). Searchable encryption revisited: Con-
sistency properties, relation to anonymous ibe, and ex-
tensions. In CRYPTO, volume 3621 of LNCS, pages
205–222.
Abdalla, M., Bellare, M., and Neven, G. (2010). Robust en-
cryption. In TCC, volume 5978 of LNCS, pages 480–
497.
Baek, J., Safavi-Naini, R., and Susilo, W. (2006). On the
integration of public key data encryption and public
key encryption with keyword search. In ISC, volume
4176 of LNCS, pages 217–232.
Baek, J., Safavi-Naini, R., and Susilo, W. (2008). Public key
encryption with keyword search revisited. In ICCSA,
volume 5072 of LNCS, pages 1249–1259.
Boneh, D., Di Crescenzo, G., Ostrovsky, R., and Per-
siano, G. (2004). Public key encryption with keyword
search. In EuroCrypt, volume 3027 of LNCS, pages
506–522.
Boyen, X. and Waters, B. (2006). Anonymous hierarchical
identity-based encryption (without random oracles).
In CRYPTO, volume 4117 of LNCS, pages 290–307.
Canetti, R., Goldreich, O., and Halevi, S. (2004). The ran-
dom oracle methodology, revisited. Journal of the
ACM (JACM), 51(4):557–594.
Chen, J., Lim, H., Ling, S., Wang, H., and Wee, H. (2012).
Shorter ibe and signatures via asymmetric pairings. In
Pairing, volume 7708 of LNCS, pages 122–140.
Chen, Y., Zhang, J., Lin, D., and Zhang, Z. (2014). Generic
constructions of integrated pke and peks. Designs,
Codes and Cryptography, pages 1–34.
Crescenzo, G. D. and Saraswat, V. (2007). Public key en-
cryption with searchable keywords based on jacobi
symbols. In IndoCrypt, volume 4859 of LNCS, pages
282–296.
Dodis, Y. and Katz, J. (2005). Chosen-ciphertext security of
multiple encryption. In TCC, volume 3378 of LNCS,
pages 188–209.
Fuhr, T. and Paillier, P. (2007). Decryptable searchable en-
cryption. In ProvSec, pages 228–236.
Ibraimi, L., Nikova, S., Hartel, P., and Jonker, W. (2011).
Public-key encryption with delegated search. In
ACNS, pages 532–549.
Kurosawa, K. (2002). Multi-recipient public-key encryp-
tion with shortened ciphertext. In PKC, pages 48–63.
Lu, W., Swaminathan, A., Varna, A. L., and Wu, M.
(2009). Enabling search over encrypted multimedia
databases. In IS&T/SPIE Electronic Imaging, pages
725418–725418. International Society for Optics and
Photonics.
Okamoto, T. and Takashima, K. (2010). Fully secure func-
tional encryption with general relations from the deci-
sional linear assumption. In CRYPTO, volume 6223
of LNCS, pages 191–208.
Shmueli, E., Vaisenberg, R., Elovici, Y., and Glezer, C.
(2010). Database encryption: an overview of con-
temporary challenges and design considerations. ACM
SIGMOD Record, 38(3):29–34.
Zhang, R. and Imai, H. (2007). Generic combination of
public key encryption with keyword search and pub-
lic key encryption. In CANS, volume 4856 of LNCS,
pages 159–174.
PracticalandSecureIntegratedPKE+PEKSwithKeywordPrivacy
453
