
Multi-objective Optimization for Control and Process Operation
Helem Sabina S
´
anchez and Ramon Vilanova
Departament de Telecomunicaci
´
o i Enginyeria de Sistemes, Universitat Aut
`
onoma de Barcelona,
08193 Bellaterra, Barcelona, Spain
1 STAGE OF THE RESEARCH
It is well known, that satisfying the requirements
and constraints required by a control engineering sys-
tem in many cases is a difficult task to fulfilling for
each of the objectives. Owing to this, this research
aims to apply the Multi-objective Optimization De-
sign (MOOD) procedure to PID controller tunning by
means Multi-Objective Optimization based on deter-
ministic algorithm. This procedure is focus on pro-
vide reasonable trade-off solution among the objec-
tives in conflictive. Currently, we are working on con-
tribution based on: an approach on the MOO pro-
cess for PI controller, applying the methodolgy to
Fractional-order PID controllers and doing a research
stay at the University of Brescia (UNIBS), Italy.
2 OUTLINE OF OBJECTIVES
The following aims are defined for the development
of this research:
• First Year:
– Review of the state of art. Existing methods
and approaches for the planning and the defini-
tion of a Multi-Objective Optimization (MOO)
process and MOOD procedure. To have an idea
of the work done and the work to be done.
– Identifying methodologies and tools needed to
solve optimization problems. Test differents al-
gorithms according to the preferences.
– Limitations on the search domain and func-
tional constraints linked to the operation of the
system.
– Select the methodology (algorithm and the de-
cision making technique).
• Second Year:
– Applications on controller tunning: PI, PID
controlllers (set-point step response).
– Consider both operation modes (set-point and
load disturbance).
– Collaborative work with others research group
dedicate to Optimization.
• Currently:
– Contribution on MOO process (new methodol-
ogy).
– Validation of the new methodology (bench-
mark, FOPID and others).
3 RESEARCH PROBLEM
This proposal seeks to develop a methodology to ad-
dress issues of control and operation of processes by
implementing a MOOD procedure. In a control sys-
tem there are different measures and indexes that are
made in order to measure their performance. Satisfy-
ing the specifications and constraints required is of-
ten a challenge. Sometimes, the improvement in per-
formance of one of them is at the expense of wors-
ening another. This kind of problems where the de-
signer have to deal with the fulfillment of multiple
objectives are known as Multi-Objective Problems
(MOPs). Such problems can be addressed using a si-
multaneous optimization of all targets. This implies
to seek for a Pareto optimal solution which the objec-
tives have been improved as possible without giving
anything in exchange. To guarantee the overall per-
formance of a MOOD procedure the following steps
are necessary: 1) definition of the MOP, 2) the MOO
process to approximate the so-called Pareto set and 3)
a Multi-criteria Decision Making (MCDM) is carried
out in order to implement the most preferable solu-
tion from the set. The MOOD procedure brings to the
designer the possibility to appreciate the trade-off of
the objectives (conflictive) this characteristic can be
useful for controller tunning.
4 STATE OF THE ART
The design of a PI-PID control system starts from a
model of the process to be controlled and a set of re-
11
Sabina Sánchez H. and Vilanova R..
Multi-objective Optimization for Control and Process Operation.
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

quirements to be satisfied. These requirements often
enter into conflict making the task of finding the ap-
propriate controller parameters not an easy task. It is
on that basis that constrained optimization can enter
into play by helping to delimit the tradeoff between
possible conflicting requirements. Such requirements
use to be the conflicting performance and robustness
specifications (in the different forms that they can be
established). Typical control system requirements in-
clude performance specifications on load disturbance
attenuation, robustness, control input usage, set-point
response and measurement noise. It is a fact that dis-
turbance rejection is of primary interest in process
control, where what really matters is steady-state reg-
ulate. On the other hand set-point changes are likely
to occur. In such cases it is possible to tackle them by
using an appropriate two-degree-of-freedom (2-DoF)
architecture. Therefore, when introducing time re-
sponse performance requirements we can confine our-
selves to disturbance attenuation. In fact, as a feed-
back property, disturbance attenuation will enter into
conflict with robustness as both are determined by
the controller parameters that appear in the feedback
loop. From a purely optimization problem point of
view, all such requirements could be used to establish
the set up of a Multiobjective Optimization Problem
(MOP). In some cases, the high performance is not
compatible with a robust controller for process vari-
ations. The controller design can be viewed as the
search for the best compromise between all the spec-
ifications and thereby the idea of multiobjective opti-
mization (MOO) can be an alternative to resolve this
problem (Mart
´
ınez et al., 2006). MOO provides the
possibility of a better selection of the final solution as
there is no part ignored in the search space. The final
solutions (Pareto set), represents the whole space of
the design variables and their projection in the space
of objectives as the Pareto front.
4.1 Multi-objective Optimization -MOO
A multi-objective optimization problem (MOP) can
be handled by performing a simultaneous optimiza-
tion of all objectives. This implies the existence of a
set of solutions, where no one is better than the oth-
ers, but differ in the degree of performance between
the objectives (Miettinen, 1998). This set of solutions
will offer a higher degree of flexibility at the decision
making stage. The role of the designer is to select the
most preferable solution according to his (her) needs
and preferences for a particular situation. A MOP,
without loss of generality (since a maximization prob-
lem can be converted to a minimization problem), can
be stated as follows:
min
θ∈ℜ
n
J (θ) = [J
1
(θ), . . . , J
m
(θ)] ∈ ℜ
m
(1)
Therefore a set of Pareto-optimal solutions is de-
fined as the Pareto set Θ
P
and its projection into
the objective space is known as the Pareto front J
P
.
Where each solution in the Pareto front is said to be a
non-dominated and Pareto-optimal solution. In gen-
eral, it does not exist a unique solution because there
is not a solution better than other in all the objectives.
MOO techniques search for a discrete approxima-
tion Θ
∗
P
of the Pareto set Θ
P
capable of generate a
good quality description of the Pareto front J
∗
P
. In
this way, the decision maker (or simply the designer)
can analyze the set and select the most preferable so-
lution.
A general framework is required to successfully
incorporate the MOO approach into any engineering
process. A multiobjective optimization engineering
design (MOOD) methodology consists (at least) of
three main steps (Reynoso-Meza et al., 2014b): the
MOOP definition (objectives, decision variables and
constraints), the MOO process (optimizer selection)
and the decision-making (DM) stage (analysis and se-
lection of the calculated solutions).
4.2 Multiobjective Problem Definition
Requirements often include specification on load dis-
turbance compensation, set-point following and ro-
bustness to process uncertainty.
Reasonably the most basic MOP statement for
PID controller tuning goals could be represented as:
θ
c
= [K
p
, T
i
, T
d
] (2)
Where θ
c
are the parameters of the optimal PID con-
troller.
minJ (θ
c
) = [J
1
(θ
c
), J
2
(θ
c
)] (3)
J
1
(θ
c
) = Per f ormance(θ
c
)
J
2
(θ
c
) = Robustness(θ
c
)
Control performance J
1
(θ
c
) can be characterized by
the integrated absolute error
IAE =
∞
Z
0
|
e(t)
|
dt, (4)
where e is the control error due to a unit step load dis-
turbance. It is a good performance measure for con-
trol system with integral action.
In order to measure the smoothness of the control ac-
tion we have the control signal total variation J
2
(θ
c
)
is defined as
TV
u
=
∞
∑
k=1
u(k + 1) − u(k) (5)
ICINCO2015-DoctoralConsortium
12

The maximum sensitivity is an indication of the sys-
tem robustness (relative stability):
M
s
= max
w
1
1 +C
y
( jw)P( jw)
(6)
where C
y
is the feedback controller transfer function,
P is the controlled process.
In some experiments we propose to use the inte-
grated square error (ISE) as a measure of performance
for the set-point and load disturbance step responses
(as in (Arrieta et al., 2010)) and the maximum sensi-
tivity (6) as a constraint of MOOP.
ISE
sp
=
∞
Z
0
e
2
(t)dt, d = 0 (7)
is the integrated square error when a set-point step
response is considered,
ISE
ld
=
∞
Z
0
e
2
(t)dt, r = 0 (8)
5 METHODOLOGY
In this section a brief description about the algorithms
used to calculated the Pareto front approximation and
the MCDM technique implemented to select a trade-
off point from the Pareto front as the final solution
to the MOP. Both of them have shown to be useful
for PI and PID controllers in (S
´
anchez and Vilanova,
2013a; S
´
anchez and Vilanova, 2013b; S
´
anchez and
Vilanova, 2014; S
´
anchez et al., 2014; Reynoso-Meza
et al., 2014a; S
´
anchez et al., 2013).
5.1 Normal Normalized Constraint for
Multi-objective Optimization
This algorithm is used to determine the Pareto front
and the set of optimal solutions. Using this algo-
rithm, the optimization problem is separated into sev-
eral constrained single optimization problems. After
series optimizations, a set of evenly distributed Pareto
solutions results. The NNC method incorporates a
critical linear mapping of the design objectives. This
mapping has the desirable property that the resulting
performance of the method is entirely independent
of the design objectives scales and in the ability to
generate a well distributed set of Pareto points even
in numerically demanding situations (Messac et al.,
2003b). The NNC method is presented here to solve
a bi-objectives problem, but it can be generalized to
n-objectives. An extract of the algorithm is presented,
for more details about the method see (Messac et al.,
2003a). The algorithm is available in Matlab Central.
1 Generate the anchor points J|
i
(x) for each
objective;
2 Calculate the Utopian Point and NADIR;
3 Normalized the objective space;
4 Generate the utopian hyperplane;
5 Definition of the normalized increments;
6 Generate the utopian lines;
7 while normalized increments do
8 Optimize;
9 end
10 Algorithm concludes. J
P
is approximated by
J
∗
P
= A|
G
;
Algorithm 1: NNC Algorithm outline.
5.2 Nash Solution-NS
All the points of the Pareto front are equally accept-
able solutions. Thus, there is the need to choose one
of such point as the final solution to the MOOP. This
is the last part of the MOOD procedure, the decision-
making stage. For this purpose we propose the Nash
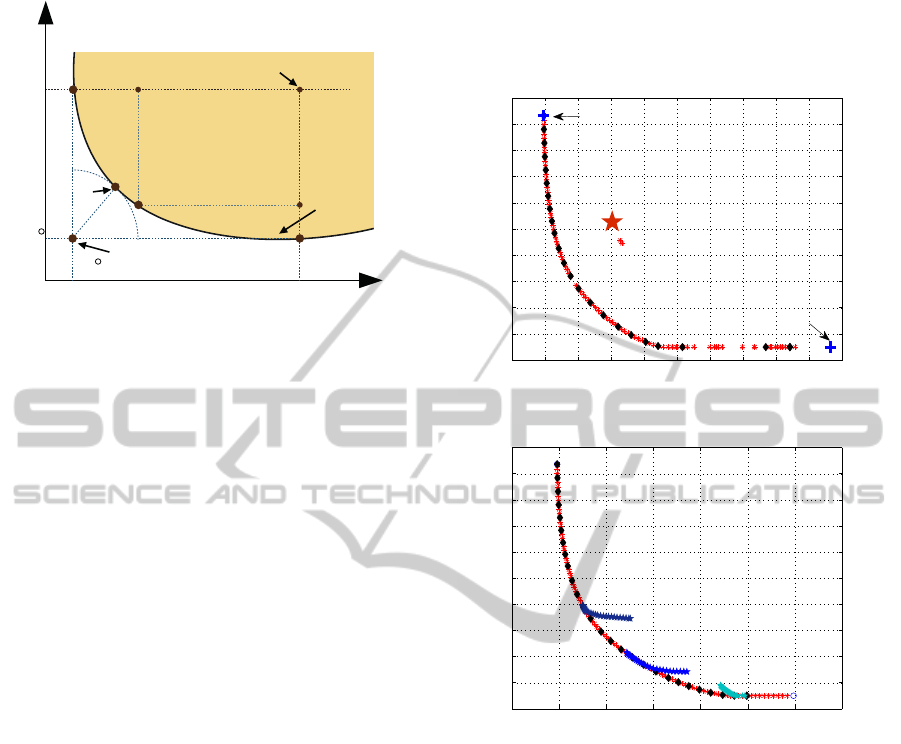
(NS) criteria, for which a graphical explanation can
be seen in Figure 1. In order to understand this op-
tion, we introduce what can be called the disagree-
ment point. If we think on both objectives indepen-
dently, none of them would agree on this point as a
common solution because it represents the worst sit-
uation. In addition, this selection can be improved
with respect of both objectives. On that basis, the
area of the rectangle defined by the points (NS, A,
B) and the disagreement point provides a measure of
the amount of solutions the NS point improves with
respect to both objectives simultaneously. The NS is
the solution that maximizes such area, this denomi-
nation comes from identifying this point as the Nash
Solution on a bargaining game among both objectives
(Aumann and Hart, 1994).
6 EXPECTED OUTCOME
This thesis contains a research line in MOO process,
focuses on controller tunning applications. For this
reason it is expecting the following contributions:
• Cover the theorical background required for this
thesis.
• Develop a methodology to apply for the controller
tunning (algorithm and MCDM technique).
Multi-objectiveOptimizationforControlandProcessOperation
13
J
J
J
J J
J
2
2
2
1 1
1
B
ANS
CS
Disagreement Point
Utopia point
Pareto
front
*
*
Figure 1: The Nash solution for a bi-objective case.
• Identify gaps that exist on the methodologies of
the MOOD procedure.
• Applying the selected tools for the controller
tunning: 1) Proportional-Integral (PI) con-
trollers, 2) Proportional-Integral-Derivative (PID)
controllers, 3) Fractional-Order Proportional-
Integral-Derivative (FOPID) controllers.
• Implement the MOOD procedure in case of stud-
ies (benchmark).
• Develop proposals on tools to improve the usua-
bility and performance of the MOOD procedure.
• Nevertheless, during the develop of this thesis:
collaborations with other research groups it will
be carried out.
• Publishing the results.
This thesis is dedicated to find the methodology
and techniques to address problems of control and op-
eration of processes through the application of multi-
objective optimization strategies. Some of the contri-
butions are listed bellow.
6.1 Correlation Between TV and M
s
(S
´
anchez and Vilanova, 2013a)
Figure (2) shows the pareto front that results for a pro-
cess model with K = 1 and τ
o
= 0.5. Anchor points
and the location of a Ziegler-Nichols tuning are also
shown. In this case, we do not have any constraint on
the robustness. Just performance is considered.
Instead, if we add as a robustness constraint, three
usual values for M
s
, for example M
s
= {1.4, 1.6, 1.8};
what we are doing is constraining the achievable sys-
tem performance. This is shown in figure (3), where
the new Pareto sets corresponding to each one of the
robustness levels are jointly shown with the uncon-
strained one. As it is seen, we get a new pareto front,
considerably smaller than the previous one, constrain-
ing ourselves to a really small set of possible solu-
tions.
0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3
0.06
0.07
0.08
0.09
0.1
0.11
0.12
0.13
0.14
0.15
0.16
IAE
TV
Pareto front
ZN
Anchor
Point
Anchor
Point
Figure 2: Pareto front for K = 1 and τ
o
= 0.5.
0.4 0.5 0.6 0.7 0.8 0.9 1
0.06
0.07
0.08
0.09
0.1
0.11
0.12
0.13
0.14
0.15
0.16
IAE
TV
Ms=1.8
Ms=1.6
Ms=1.4
Figure 3: Comparison of Pareto fronts.
Therefore, there is a correlation between the value
of M
s
and the control input usage in terms of TV . Ef-
fectively, as pointed out in (Foley et al., 2005) there
do exists a correlation. This is clearly shown in fig-
ure (4) for the example at hand. We can therefore di-
rectly associate the robustness to the TV performance
index and think on that index not just as the input us-
age but also as a measure of the closed system ro-
bustness. From figure (4) the approximate relation is
established M
s
≈ 10.5TV + 0.77. This allows to think
on the multi objective optimization problem simply as
a tradeoff between TV and J
IAE
, having in mind that
the selection of the appropriate point form the pareto
front will need to take into account the level of robust-
ness we need (lower values for TV ). Effectively this
simplifies the setup for the optimization problem and
subsequent generation of the pareto front.
ICINCO2015-DoctoralConsortium
14
0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13 0.14 0.15 0.16
1.4
1.5
1.6
1.7
1.8
1.9
2
2.1
2.2
2.3
2.4
TV
M
s
Figure 4: TV and M
s
correlation, M
s
≈ 10.5TV + 0.77.
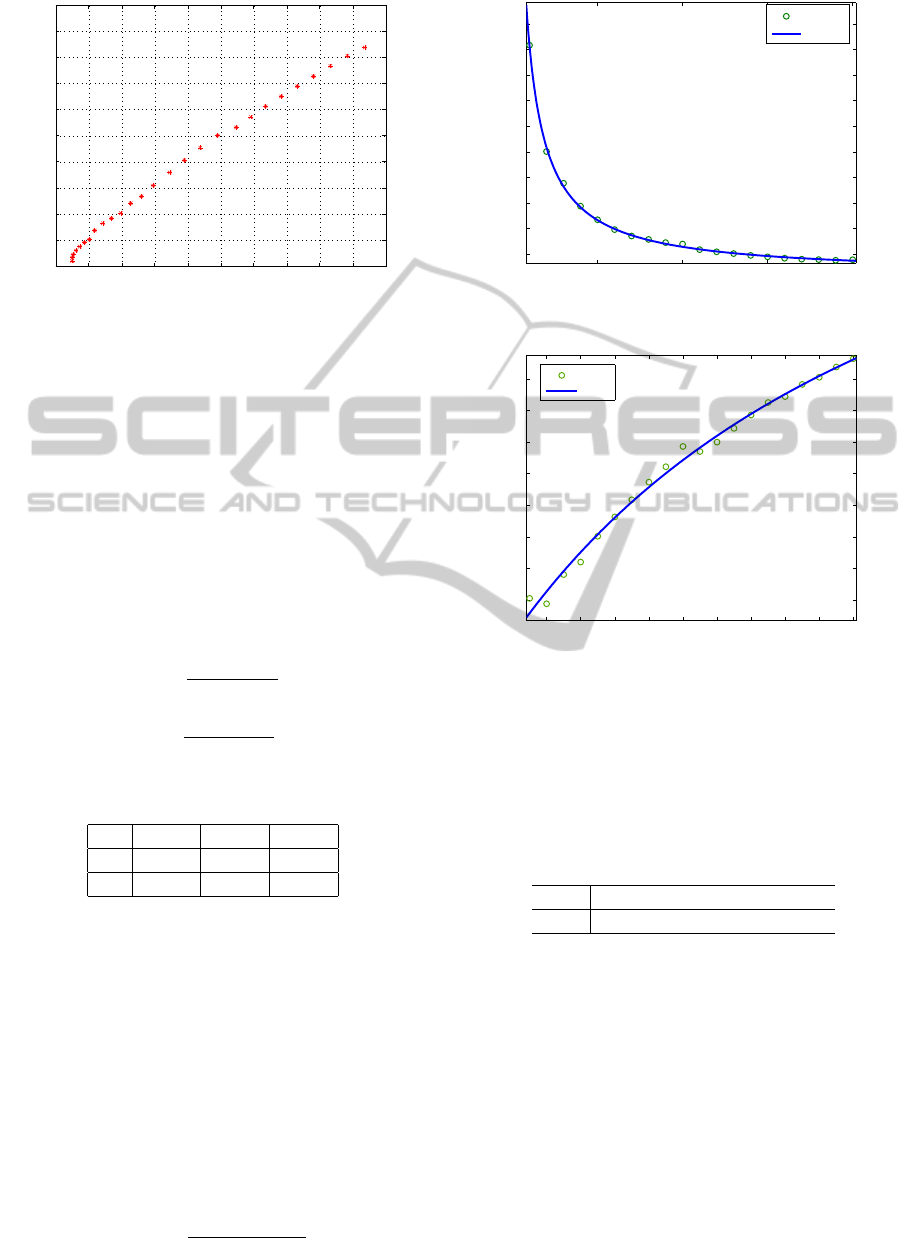
6.2 Nash-based PI Tuning (S
´
anchez and
Vilanova, 2013b)
The values of τ
o
are selected to take the FOPDT pro-
cesses with small, medium and fairly long dead time
into account, the values of the normalized dead-time
(τ
o
) are considered from 0.1 to 2. To obtain appropri-
ate values of κ
p
and τ
i
for a specified value of τ
o
, non-
dominated solutions are determined using the NNC
method. Finally, when we obtain the Pareto front one
optimal solution is choosen known as Nash solution.
The tuning formulae is as follows:
κ
p
=
a
0
∗ τ
o
+ a
1
τ
o
+ b
0
, (9)
τ
i
=
a
0
∗ τ
0
+ a
1
τ
0
+ b
0
, (10)
Table 1: Controller constants for κ
p
and τ
i
.
a
0
a
1
b
0
κ
p
0.098 0.565 0.026
τ
i
2.624 1.548 2.649
The constants in equations (9-10) are shown in Ta-
ble 1. The fitting obtained using this formulae are also
shown in figures (5-6).
6.3 Comparison Between
Multi-objective Optimization
Techniques (S
´
anchez and Vilanova,
2014)
Consider the four-order controlled benchmark pro-
cess proposed in (
˚
Astr
¨
om and H
¨
agglund, 2000) and
given by the transfer function
P
α
(s) =
1
∏
3
n=0
(α
n
s + 1)
(11)
0.5 1 1.5 2
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
τ
o
κ
p
κ
p
vs. τ
o
fit
Figure 5: Normalized controller gain.
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
τ
o
τ
i
τ
i
vs. τ
o
fit
Figure 6: Normalized controller integral time.
with α ∈
{
0.1, 0.5, 1.0
}
. Using the three-point identi-
fication procedure 123c (Alfaro, 2006) FOPDT mod-
els have been obtained whose parameters are shown
in Table 2. These models will be used for PI con-
troller design.
Table 2: Example - FOPDT Models.
α K T L τ
o
0.50 1 1.247 0.691 0.554
• Case 1: The pareto front was obtained using the
NNC and a reference point (Ziegler-Nichols as a
initial point), using the ZN tunning rule (K
p
=
1.62T
i
= 2.30), this solution is dominated by other
solutions as we can see in figure (7)
• Case 2: The pareto front was calculated with the
Multiobjective Differential Evolution Algorithm
with Spherical Pruning (sp-MODE) using perti-
nence criteria. This concept refers to the abil-
ity to give a practical solution from the point of
view of the designer. In this case, the Pareto front
is bounded, if it is known a priori which solu-
tions are looking for and are interesting for the
Multi-objectiveOptimizationforControlandProcessOperation
15

designer. It is a useful option when you know that
in some cases, improving one objective does not
justify the severe degradation in the other. The
values (IAE = 0.9217 TV = 0.1319) were used as
the pertinence criteria. They were calculated with
the parameters mentioned before. In figure (8) it
is possible to see how the algorithm focuse the
search only in the range that contains the values
of pertinence.
• Case 3: We use the sp-MODE but this time with-
out of pertinence, see figure (9).
Table 3: Example - Controller Parameters.
α = 0.5
Methods Kp Ti
Case 1: NNC 1.34 1.86
Case 2: sp-MODE (pertinence) 1.05 1.18
Case 3: sp-MODE 0.84 1.37
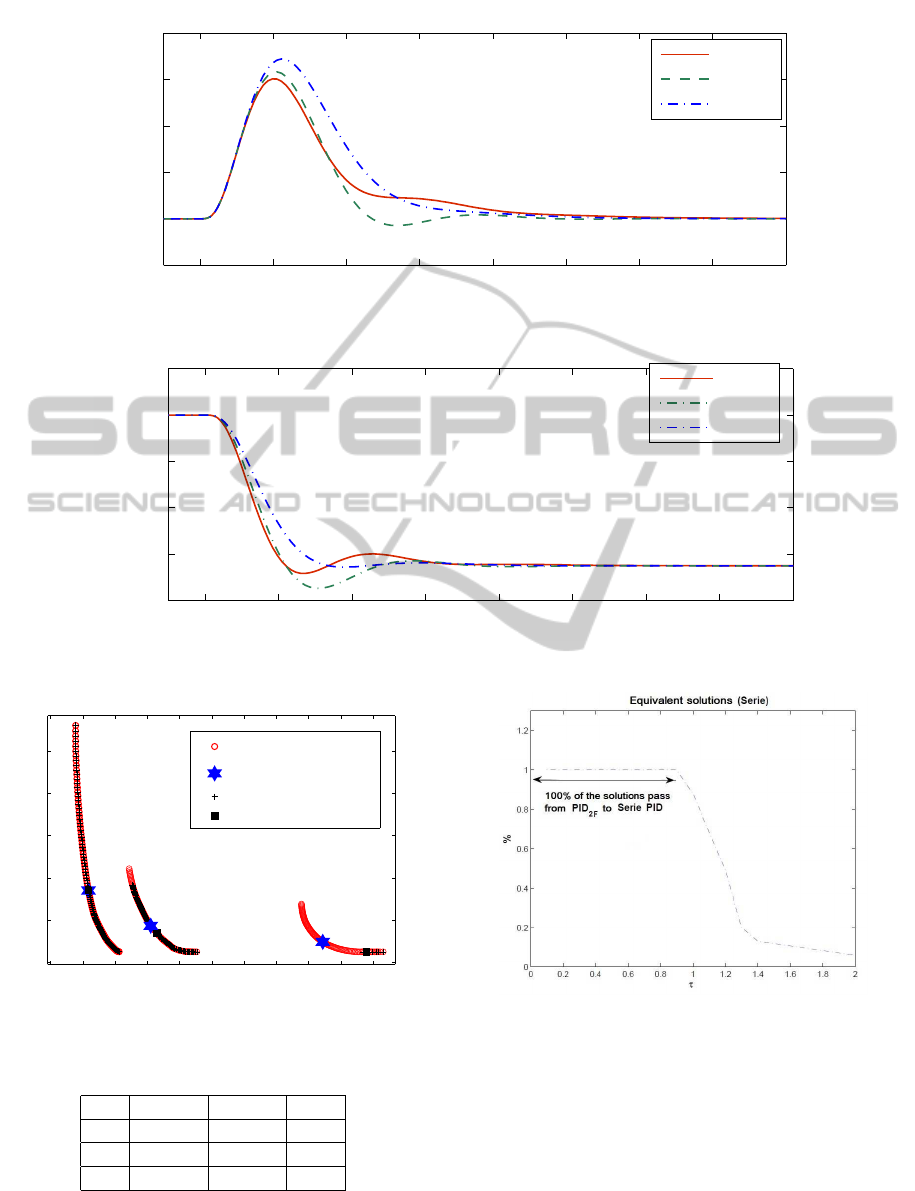
For each one of these cases the Nash solution was
calculated, therefore in Table 3 the parameters of the
controller (PI) are shown and in Table 4 the values
of performance and robustness of the system are dis-
played. Furthermore, figure (10) shows the achieved
time response when facing a step load-disturbance.
Table 4: Example - Performance and Robustness.
Case 1 Case 2 Case 3:
NNC sp-MODE (pertinence) sp-MODE
τ
0=0.5
IAE 0.9022 0.7662 1.0601
TV 0.1023 0.1118 0.0856
M
s
1.64 1.67 1.44
Y
max
0.3016 0.3167 0.3446
0.5 1 1.5 2
0.08
0.1
0.12
0.14
0.16
0.18
0.2
NASH
IAE
TV
Pareto Front (model corresponding to α=0.5)
ZN
Figure 7: Pareto front for the process model corresponding
to α = 0.5 (Case 1).
0.65 0.7 0.75 0.8 0.85 0.9 0.95 1
0.085
0.09
0.095
0.1
0.105
0.11
0.115
0.12
0.125
0.13
0.135
IAE
TV
Frente de Pareto (modelo correspondiente a =0.5)
NASH
Figure 8: Pareto front for the process model corresponding
to α = 0.5 (Case 2).
0 5 10 15 20 25 30 35 40 45 50
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
IAE
TV
Pareto Front (model corresponding to α=0.5)
NASH
Figure 9: Pareto front for the process model corresponding
to α = 0.5 (Case 3).
6.4 Equivalence and Optimality for PID
Controllers (S
´
anchez et al., 2014)
Based on the initial work of ((Alfaro and Vilanova,
2012)) where the differet formulations for PID con-
trollers are listed and conversion formulae is pro-
vided, the equivalence between them, is analyzed
here.
The optimization was applied to the most gen-
eral configuration PID
2F
from τ = [0.1 − 2.0]. Here
we only present 3 representative cases of τ =
[0.6, 1.0, 2.0], the Pareto front is shown in Figure 11.
It can be seen that when the normalized dead time in-
creases the IAE index as well.
Furthermore, the total variation (TV) is decreasing
while also the robustness of the system is higher. In
((S
´
anchez and Vilanova, 2013a)) some experiments
shows that there is correlations between both of them.
This can be see in Table (5-6), where the values of
performance and robustness are shown for each con-
figuration and its respective τ. In Figure (11) is also
ICINCO2015-DoctoralConsortium
16
10 12 14 16 18 20 22 24 26
−0.1
0
0.1
0.2
0.3
0.4
y(t)
Output to a unit load−disturbance
t(s)
Case 1
Case 2
Case 3
10 12 14 16 18 20 22 24 26
−0.8
−0.6
−0.4
−0.2
0
0.2
t(s)
Control Signal
u(t)
Case 1
Case 2
Case 3
Figure 10: Time output and control responses for α = 0.5.
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 2.2
0.06
0.08
0.1
0.12
0.14
0.16
IAE
TV
Pareto Fronts and Nash Solutions
Ideal with Filter (PID
2
F)
Nash Solution (PID
2
F)
Equivalent Serie
Nash Solution (Serie)
Figure 11: Pareto Front and Nash Solution.
Table 5: Performance and Robustness (PID
2F
y PID
2
).
τ
0
IAE TV M
s
0.6 0.4348 0.0940 1.69
1.0 0.8571 0.0740 1.51
2.0 2.1583 0.0650 1.42
shown the Series equivalent for PID
2F
y PID
2
.
It is worth mentioning, that when it passed from
Figure 12: Equivalent solutions from a PID
2F
to Serie PID.
PID
2F
configuration to the PID
2
, all the solutions had
the equivalent; owing to this both configurations have
the same Nash solution. In Figure (12) we see that
the equivalent solutions for the series configuration
are less as τ increases, in this cases the Nash solutions
will not be the same for the Series PID see Table (6).
Multi-objectiveOptimizationforControlandProcessOperation
17
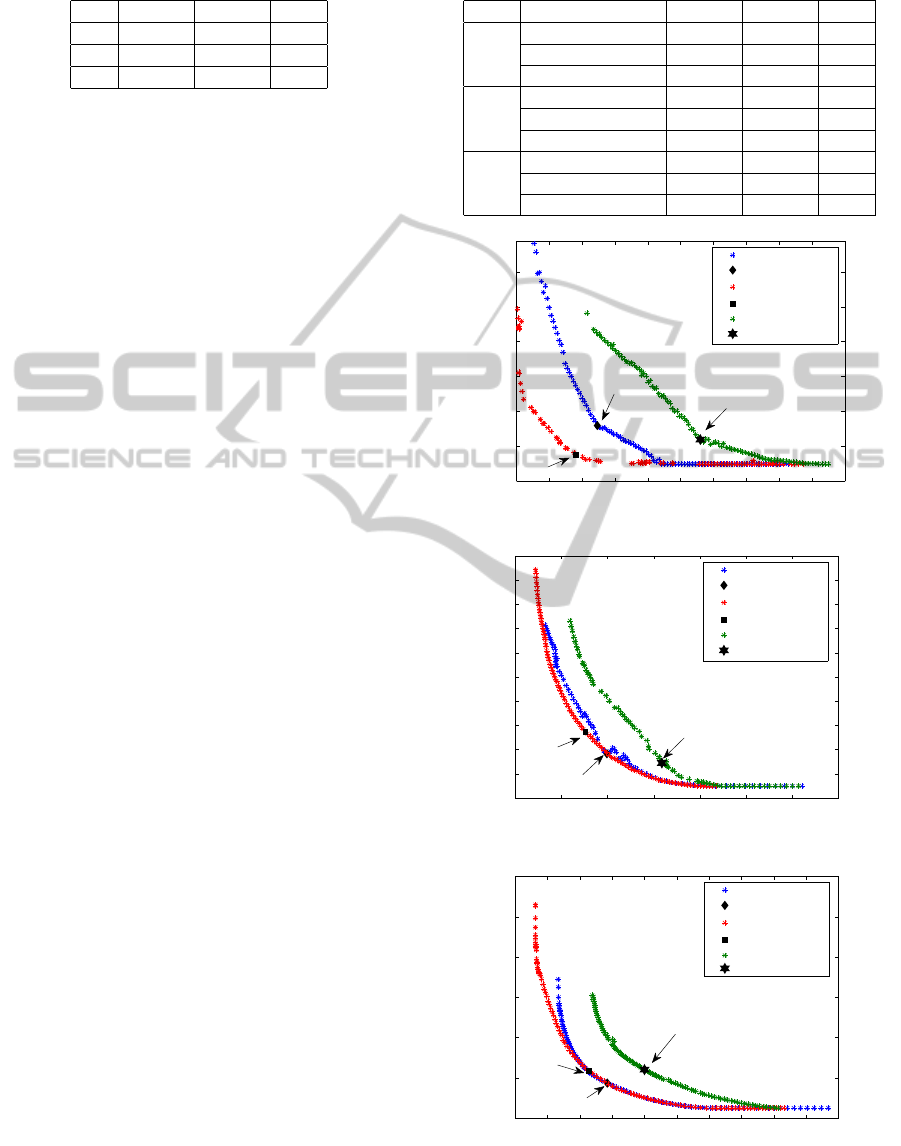
Table 6: Performance and Robustness (Serie).
τ
0
IAE TV M
s
0.6 0.4348 0.0940 1.69
1.0 0.8206 0.0773 1.53
2.0 1.8869 0.0697 1.48
6.5 Optimality Comparison of PID
Implementations (S
´
anchez and
Vilanova, 2014)
The Pareto front for each configuration was calculated
with normalized dead times from 0.1 to 2.0. But in
this paper only three representative cases (0.1, 0.75
and 1.75) are presented. The Pareto fronts are shown
in figure 13.
The displacement of the Pareto fronts of each con-
figuration shows the behavior of the PID algorithm
from a general to a more constrained PID configura-
tion. As it can be seen as the τ
0
increases, the Pareto
fronts; Figure (13); are getting closer between each
other but always dominated by the PID
2F
configura-
tion. The superiority of this configuration regarding
the Standard one increases as τ
0
decreases. However
both configurations show a clear superiority with re-
spect to the series one. As shown in Table (7) the
values of performance and robustness for each case
are different, sometimes the 2DoF PID Standard and
Ideal with filter have similar values compared to the
Series configuration.
With the experiments performed in this work we
realized that if we want a better functionality, it is
not necessary to use the conversion formulae. For ex-
ample see in Figure (13a), if we apply the equations
to the 2DoF Series configuration in order to obtain
a PID
2F
, the results of the performance and robust-
ness will be the same as the 2DoF Series (the new
Pareto front calculated would be at the same position
as the Series configuration). This means that instead
of applying the conversion formulae we could tune
the controller again in order to obtain a better perfor-
mance, robustness and also less overshoot. Overall,
this representation by the Pareto front allows us to see
how important is to see the behavior of this indexes
(IAE, TV, M
s
).
6.6 Reliability based Multiobjective
Optimization Design Procedure for
PI Controller Tunning
(Reynoso-Meza et al., 2014a)
This was a collaborative work, we presented a MOOD
procedure involving a reliability based MOOP state-
Table 7: Controller performance.
τ
0
Controller IAE TV M
s
0.1
Standard 1.3534 0.1725 1.51
Series 1.4007 0.1679 1.46
Ideal with Filter 1.3365 0.1713 1.44
0.75
Standard 2.7298 0.1994 1.53
Series 3.2146 0.1774 1.52
Ideal with Filter 2.5964 0.2197 1.62
1.75
Standard 5.3946 0.1876 1.57
Series 5.9093 0.1913 1.58
Ideal with Filter 5.2701 0.1986 1.67
0.095 0.1 0.105 0.11 0.115 0.12 0.125 0.13 0.135 0.14 0.145
0.064
0.066
0.068
0.07
0.072
0.074
0.076
IAE
TV
Standard
M
s
=1.51
Ideal with Filter (ID
wf
)
M
s
=1.44
Series
M
s
=1.46
Standard
Series
ID
wf
(a) Pareto Front τ
0
= 0.1
0.4 0.5 0.6 0.7 0.8 0.9 1 1.1
0.06
0.07
0.08
0.09
0.1
0.11
0.12
0.13
0.14
0.15
0.16
IAE
TV
Standard
M
s
=1.53
Ideal with filter (ID
wf
)
M
s
=1.62
Series
M
s
=1.52
Series
Standard
ID
wf
(b) Pareto Front τ
0
= 0.75
1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 2.1 2.2
0.06
0.08
0.1
0.12
0.14
0.16
0.18
IAE
TV
Standard
M
s
=1.57
Ideal with filter (ID
wf
)
M
s
=1.67
Series
Ms=1.58
Standard
ID
wf
Series
(c) Pareto Front τ
0
= 1.75
Figure 13: Pareto Front for differents τ
0
.
ICINCO2015-DoctoralConsortium
18
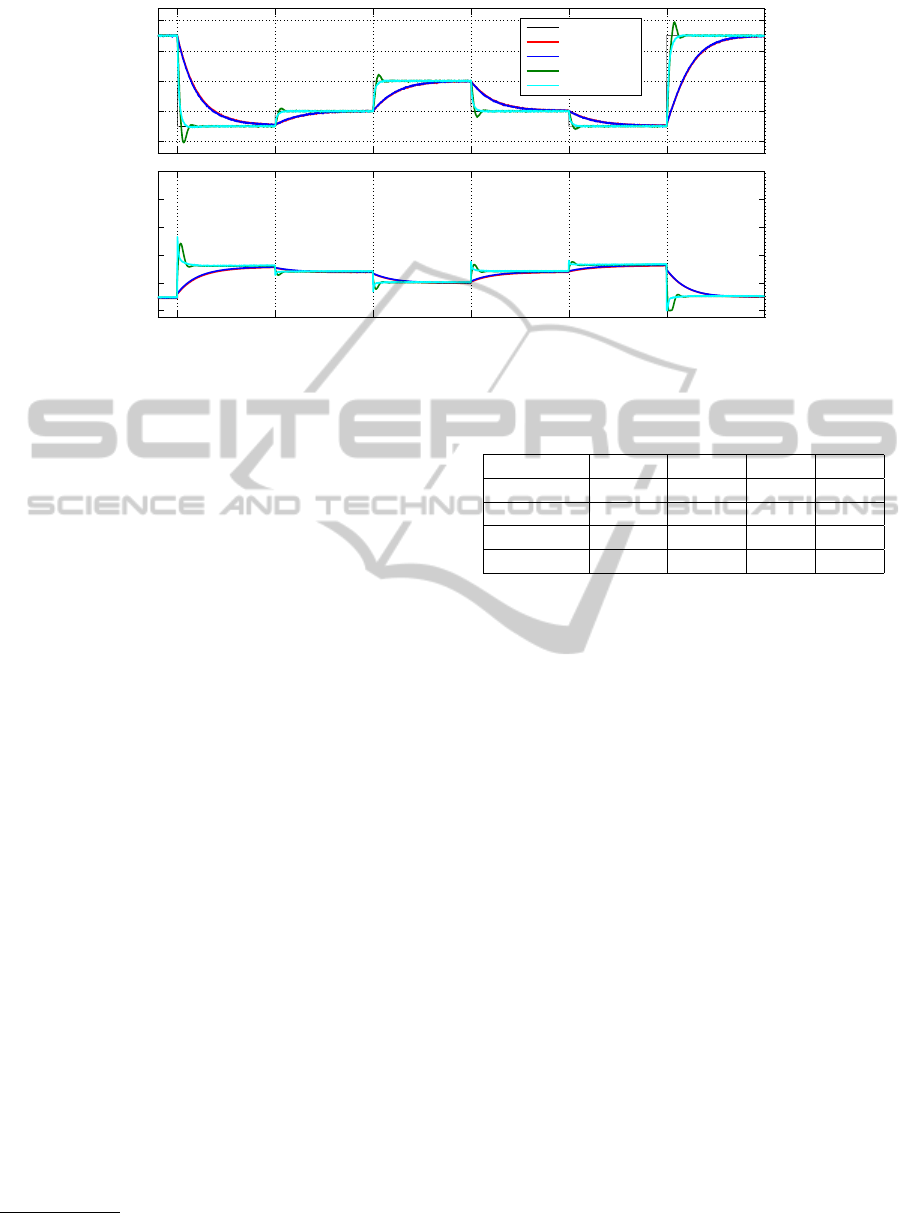
100 200 300 400 500 600 700
−10
−5
0
5
10
Temperature [ºC]
100 200 300 400 500 600 700
0
20
40
60
80
100
Time [sec]
U [%]
Reference
Controller IS
Controller NS−2D
Controller NS−3D
Controller LD−3D
Figure 14: Performance comparison on the Peltier Cell.
ment for controller tuning. To improve the results
in the MOO process an hybrid approach has been
proposed to calculate the Pareto front approximation.
Merging deterministic and evolutionary algorithms,
the Normalized Normal Constraint (NNC) and the
Multiobjective Differential Algorithm with Spherical
Pruning (sp-MODE), respectively. A Peltier cell was
chosen to evaluate the above, mentioned MOOD pro-
cedure. First we generate the preliminary bi-objective
Pareto front J
0∗
P
with the NNC algorithm. With such
Pareto front, two solutions are selected for further
evaluation: the initial solution employed in the op-
timization process and the Nash-based (IS
1
and NS-
2D
2
respectively). In the execution using the sp-
MODE and the Pareto front approximation from NNC
algorithm, pertinency is included in the algorithm to
bound the new objective using the starting solution
of the NNC algorithm. Two solutions were selected:
Nash-based and a solution selected by analyzing the
Pareto front using Level diagrams (NS-3D and LD-
3D respectively).
The performance of the selected controllers is
shown in Figure (14) and in Table (8). Whilst per-
formance of controllers IS and NS-2D are similar it is
interesting to notice differences between controllers
NS-2D and NS-3D. Both of them have been selected
using the same Decision Making (DM) rule (Nash so-
lution). Differences on the performance are due to
the additional information used in the MOP statement
minding degradation on IAE performance. Controller
LD-3D selected from the LD visualization is consis-
tent with the fact of improving IAE at expense of
more control effort (TV). The results presented val-
idate the procedure as useful for PI tuning of non-
linear systems.
1
Initial Solution
2
Nash Solution in 2D
Table 8: Controller performance on the Peltier cell case
study.
Controller K
p
T
i
IAE TV
IS 0.19 2.74 992.4 86.0
NS-2D 0.1898 2.6613 967.6 86.8
NS-3D 0.5091 0.4057 154.6 263.9
LD-3D 2.3735 3.2623 120.7 657.4
6.7 Nash Solution for Optimal Balance
of Servo/Regulation Operation in
PID Control (S
´
anchez et al., 2015)
A multi-objective optimization approach is proposed
for the tuning of one degree-of-freedom proportional-
integral-derivative controllers where both the trade-
off between the servo and regulation operation modes
and the trade-off between performance and robustness
are considered. After having quantified the loss of
performance that occurs if robustness is taken into ac-
count in the optimal design of the controller, a tuning
rule is proposed based on the Nash solution, so that
a balanced robust tuning is obtained simply starting
from a first-order-plus-dead-time model of the (self-
regulating) process.
It has been shown that, in this context, the robust-
ness of the system can be a critical issue and there-
fore it has to be included explicitly in the optimization
procedure. Tuning rules based on the Nash solutions
have also been devised so that the methodology can be
easily implemented in standard industrial controllers.
In this example we will illustrate how the imple-
mentation of the Nash tuning rules improves the ro-
bustness of the system and also maintains acceptable
values of the performance with respect to both the op-
eration modes. Consider the following process and
the corresponding FOPDT approximation ((Zhuang
Multi-objectiveOptimizationforControlandProcessOperation
19
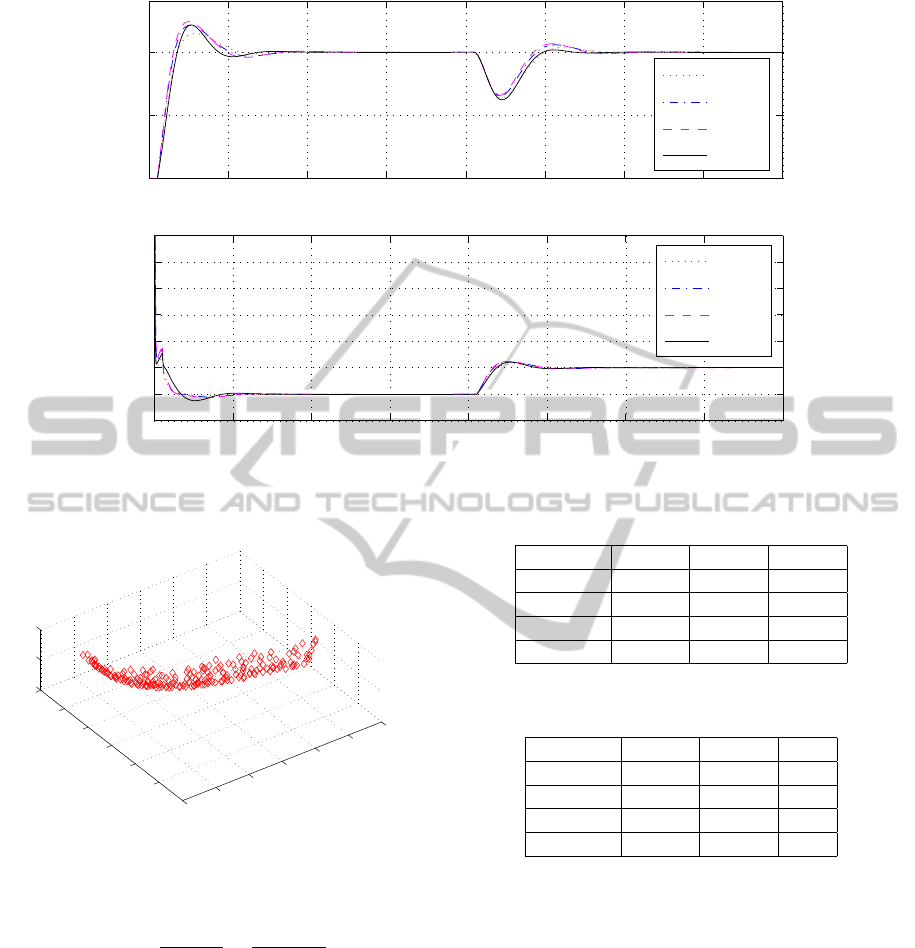
0 5 10 15 20 25 30 35 40
0
0.5
1
Time
Process Variable
0 5 10 15 20 25 30 35 40
0
1
2
3
4
5
6
7
Time
Control Variable
α=0.25
α=0.50
α=0.75
Nash
α=0.25
α=0.50
α=0.75
Nash
Figure 15: Step responses for the illustrative example.
0.09
0.1
0.11
0.12
0.13
0.14
0.15
0.35
0.4
0.45
0.5
0.55
0.6
1
1.5
2
IAE
ld
Pareto Front (τ
o
=0.1)
IAE
sp
M
s
Figure 16: Pareto front for τ = 0.1.
and Atherton, 1993)):
P(s) =
e
−0.5s
(s + 1)
2
≈
e
−0.99s
1 + 1.65s
(12)
The PID controller parameters determined by us-
ing the Nash tuning rules and the intermediate tun-
ing rules ((Arrieta et al., 2010)) are shown in Table
(9) while the corresponding performance indices and
maximum sensitivity values are shown in Table 10.
The set-point and load disturbance step responses are
plotted in Figure (15).
From the results it can be seen that the perfor-
mance obtained with the Nash tuning is similar to
that obtained with the intermediate tuning despite the
maximum sensitivity is M
s
= 1.73 for the Nash tuning
while in the other cases it ranges from 2.26 to 2.77.
Table 9: PID controller parameters.
Tuning K
p
T
i
T
d
NS 1.9652 1.6477 0.3464
α = 0.25 1.791 1.378 0.520
α = 0.5 1.949 1.234 0.527
α = 0.75 2.016 1.177 0.531
Table 10: Performance and robustness value for the system
(12).
Tuning ISE
ld
ISE
sp
M
s
NS 0.2674 1.1511 1.73
α = 0.25 0.2562 1.1133 2.26
α = 0.5 0.2265 1.1793 2.59
α = 0.75 0.2172 1.2224 2.77
6.8 Future Work
The future research efforts will be conducted:
1. FOPID Controllers: to apply the same ap-
proach we use in (S
´
anchez et al., 2015) to
Fractional-order proportional-integral-derivative
(FOPID) controllers. A MOOD procedures will
be implemented to obtain a set of tuning rules for
FOPID controllers. Using the Nash solutions as
the MCDM technique. The tuning rules will be
devised in order to minimise the integrated abso-
lute error with a constraint on the maximum sen-
sitivity. The trade-off between the perfomance in
the set-point following and in the load disturbance
rejection task it will be taking into account, a pre-
liminary result is shown in Figure (16).
ICINCO2015-DoctoralConsortium
20

2. Multistage Procedure for PI Controller Tun-
ning: a multistage approach is proposed merg-
ing a deterministic and evolutionary algorithm,
the Normalized Normal Constraint (NNC) and
Multiobjective Differential Evolution Algorithm
with Spherical Pruning (sp-MODE), respectively.
This technique is formulated through design of a
multi-objective optimization procedure, to ensure
the construction of Pareto frontier that guarantee
well distribution and exclude the non-Pareto and
local Pareto points. This procedure focuses on
reliability-based optimization instances. To val-
idate the approach, we will consider the Boiler
Control Benchmark and the Peltier cell; the re-
sults of the improvement of the performance is
demonstrated and its usefulness for controller tun-
ing.
REFERENCES
Alfaro, V. M. (2006). Low-Order Models Identification
from the Process Reaction Curve. Ciencia y Tec-
nolog
´
ıa (Costa Rica), 24(2):197–216. (in Spanish).
Alfaro, V. M. and Vilanova, R. (2012). Conversion for-
mulae and performance capabilities of two-degree-of-
freedom pid control algorithms. In Proceedings of the
17th. IEEE Conference on emerging technologies &
factory automation (ETFA).
Arrieta, O., Visioli, A., and Vilanova, R. (2010). Pid au-
totuning for weighted servo/regulation control opera-
tion. Journal of Process Control, 20(4):472–480.
˚
Astr
¨
om, K. J. and H
¨
agglund, T. (5-7 April, Terrasa, Spain,
2000). Benchmark Systems for PID Control. In IFAC
Digital Control: Past,, Present and Future of PID
Control (PID’00).
Aumann, R. and Hart, S. (1994). Handbook of Game The-
ory with Economic Applications. Elsevier.
Foley, M., Ramharack, N., and Copeland, B. (2005). Com-
parison of PI controller tuning methods. Ind. Eng.
Chem. Res., 44(17):6741–6750.
Mart
´
ınez, M. A., Sanchis, J., and Blasco, X. (2006). Mul-
tiobjective controller design handling human prefer-
ences. Engineering applications of artificial intelli-
gence, 19(8):927–938.
Messac, A., Ismail-Yahaya, A., and Mattson, C. (2003a).
The normalized normal constraint method for gener-
ating the Pareto frontier. Structural and Multidisci-
plinary Optimization, (25):86 – 98.
Messac, A., Ismail-Yahaya, A., and Mattson, C. A. (2003b).
The normalized normal constraint method for gener-
ating the pareto frontier. Structural and multidisci-
plinary optimization, 25(2):86–98.
Miettinen, K. M. (1998). Nonlinear multiobjective opti-
mization. Kluwer Academic Publishers.
Reynoso-Meza, G., S
´
anchez, H., Blasco, X., and Vilanova,
R. (2014a). Reliability based multiobjective optimiza-
tion design procedure for pi controller tuning. In 19th
World Congress The International Federation of Au-
tomatic Control, Cape Town, South Africa.
Reynoso-Meza, G., Sanchis, J., Blasco, X., and Mart
´
ınez,
M. (2014b). Controller tuning using evolutionary
multi-objective optimisation: current trends and ap-
plications. Control Engineering Practice, (DOI:
10.1016/j.conengprac.2014.03.003).
S
´
anchez, H., Reynoso-Meza, G., Vilanova, R., and Blasco,
X. (2013). Comparaci
´
on de t
´
ecnicas de optimizaci
´
on
multi-objetivo cl
´
asicas y estoc
´
asticas para el ajuste de
controladores pi (spanish). In XXXIV Jornadas de Au-
tom
´
atica, Terrassa, Barcelona, Spain.
S
´
anchez, H. and Vilanova, R. (2013a). Multiobjective tun-
ing of PI controller using the NNC method: Simpli-
fied problem definition and guidelines for decision
making. In Proceedings of the 18th IEEE Confer-
ence on Emerging Technologies & Factory Automa-
tion, Cagliary, Italy.
S
´
anchez, H. and Vilanova, R. (2013b). Nash-based criteria
for selection of pareto optimal controller. In Proceed-
ings of the 17th. International Conference on System
Theory, Control anmd Computing, Sinaia, Romania.
S
´
anchez, H. and Vilanova, R. (2014). Optimality compari-
son of 2dof PID implementations. In Proceedings of
the 18th International Conference on System Theory,
Control and Computing, Sinaia, Romania.
S
´
anchez, H., Vilanova, R., and Arrieta, O. (2014). Imple-
mentacion de controladores PID: Equivalencia y opti-
malidad (spanish). In XXXV Jornadas de Autom
´
atica,
Valencia, Spain.
S
´
anchez, H., Visioli, A., and Vilanova, R. (2015). Nash tun-
ing for optimal balance of the servo/regulation opera-
tion in robust pid control. In Mediterranean Confer-
ence on Control & Automation, Torremolinos, Spain.
Zhuang, M. and Atherton, D. P. (1993). Automatic tuning of
optimum PID controllers. IEE Proceedings - Control
Theory and Applications, 140:216–224.
Multi-objectiveOptimizationforControlandProcessOperation
21
