Applying the AHP to Smart Mobility Services: A Case Study

Roberto Boselli, Mirko Cesarini, Fabio Mercorio and Mario Mezzanzanica

Department of Statistics and Quantitative Methods - C.R.I.S.P. Research Centre, University of Milan-Bicocca, Milan, Italy

Keywords:

Decision Making, Business Intelligence, Smart City, AHP.

Abstract:

Making decision is a far from straightforward process, as it often requires to consider a number of complex

criteria whose importance relies on the experiences and the preferences of the decision makers involved.

Being able to structure and reproduce this knowledge is a challenging issue in the context of strategic decision

making, and also common BI analytics can beneﬁt from the joint use of that knowledge. As a contribution, in

this work we describe how a multi criteria decision making technique, i.e., the Analytic Hierarchy Process, has

been applied to a smart-mobility context, where the decision goal was to weight the factors that support the

innovation of a smart mobility service in the city of Milan. The AHP has been selected as it allows considering

both tangible and intangible factors that guide the decision within the model. We employed three distinct kind

of stakeholders, namely service providers, over 35, and under 35 users and we synthesised a ranking of criteria

on the basis of the preferences they provided. The results shed the light on the different judgments that each

group gives to the identiﬁed criteria in terms of both ranking and importance.

1 INTRODUCTION

Making decisions is part of everyday life, and this

process always involve a number of subtended and

implicit criteria that one draws on the past experience.

To give an example, buying a smartphone is a deci-

sion process that takes into account several criteria,

some tangible like cost, performances, battery life,

and some factors that are intangible, such as having

a comfortable grip, the style, and the past experience

with the vendor, too. All these factors affect our ﬁ-

nal decision in a way that is hard to be reproduced or

explained.

In such a scenario, the basic idea of Multi Crite-

ria Decision making (MCDM) is to provide a set of

methods that allows decision makers to structure and

to weight the criteria that guide their decision. This

activity has proved to be beneﬁcial in a large number

of real-life domains (Wu and Lee, 2007; Madas and

Zografos, 2008; Bello-Dambatta et al., 2009; Abdi

and Labib, 2003), as it enables the formalisation of

the decision process, making possible to iterate and to

validate it (e.g., to validate whether the judgments on

the criteria are sound or not) and to make evidence of

the decision process to the decision makers involved.

When prior experience is missing on formalising and

understanding complexdecision making processes in-

volving several actors, a systematic and comprehen-

sive approach as MCDM is very useful. Being able

to explain, formally motivate, and share the reasons

behind decision making is far from negligible, as it

helps obtaining a more reliable and shared decision

process.

On the other side, the smart-city context is grow-

ing in importance in both academic and industrial

communities, as it aims at improving the sustainabil-

ity and the quality of citizens’ life (see, e.g., (Nam

and Pardo, 2011)). A report of the European Com-

mission has recently listed the (most) important ele-

ments (aka dimensions) that compose the smart-city

ecosystem (Manville et al., 2014), namely: environ-

ment, people, economy, government, living, and mo-

bility. In the EU vision, the glue of all these dimen-

sions are Human, technological, and institutional fac-

tors that allow the smart-city ecosystem working.

1.1 Motivation and Contribution

In this paper we report our experience in applying

the Analytic Hierarchy Process (AHP) method (Saaty,

1988; Saaty, 1990) to a smart-mobility decision mak-

ing process. Our aim here is to extract and struc-

ture knowledge about the decision making processes

of the several mobility service stakeholders (i.e., ﬁnal

users and service provides).

In the context of strategic decision making, the use

354

Boselli R., Cesarini M., Mercorio F. and Mezzanzanica M..

Applying the AHP to Smart Mobility Services: A Case Study.

DOI: 10.5220/0005580003540361

In Proceedings of 4th International Conference on Data Management Technologies and Applications (KomIS-2015), pages 354-361

ISBN: 978-989-758-103-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

of AHP would represent an added value for classical

Business Intelligence and Analytics applications, as it

sheds the light on the dynamics that form the decision

making process (i.e., the criteria and their relative im-

portance for decisor makers). This result is quite im-

portant as in many real-life domains indicators and

analytics are not sufﬁcient to exhaustively explain the

phenomena under study. To give an example, a vari-

ant of AHP (i.e., ANP

) has been applied for select-

ing knowledge management strategies of a company

whose administrators were unable to decide how to

invest the year-proﬁts, even though a lot of indica-

tors and forecasting analyses were available, due to

the personal preferences and beliefs of each on how

to invest proﬁts. Here the ANP was helpful to guide

them in understanding and highlighting the dynam-

ics of the decisions, ﬁrst by selecting criteria, then by

evaluating each criterion and ﬁnally by summarising

a common decision (see, e.g.(Wu and Lee, 2007)).

In this paper the AHP has been applied to

three distinct groups of stakeholders, namely service

providers, over 35, and under 35 users for obtaining

the weighted criteria that would rank the enabling fac-

tors for innovating a smart-mobility service in Mi-

lan. To this end, we have built an AHP model on

the basis of the service innovation enabling factors

emerged at the CityTech meeting.

Then, we em-

ployed a number of stakeholders for weighting these

criteria. The main outcome of this work is a weighted

hierarchy of criteria that hold all the knowledge about

this group of stakeholders - in a formal, deterministic

and replicable way - regardless of the employed mo-

bility solutions. Then, a domain analyst may exploit

the weighted hierarchy of criteria to draw up a rank

of the best mobility solutions in Milan, according to

stakeholders weighted criteria.

The paper is arranged as follows. In Sec. 2 we

brieﬂy introduce some backgrounds on AHP tech-

nique and its strong/weak points with respect to our

purposes. In Sec. 3 we describe the AHP model built

in terms of criteria and sub-criteria while in Sec. 4 we

show the results obtained. Finally, the conclusions are

outlined in Sec. 5

the Analytic Network Process differs from AHP as

(1) the model is arranged as a network rather than a tree,

thus (2) it allows expressing dependences between criteria

and sub-criteria whilst independence amongst criteria is re-

quired in the AHP model

An international forum held in Milan, October 27th,

2014, see http://www.citytech.eu/

2 BACKGROUNDS ON AHP

Roughly speaking, Multi Criteria Decision Making

(MCDM) refers to a set of methods that allows con-

structing a global preference relation for a set of al-

ternatives to be evaluated by using several criteria. A

literature review on MCDM falls out the scope of this

paper, the reader can refer to (Figueira et al., 2005a)

for a survey.

The MDCM approaches are able to deal with

dependence amongst criteria (ANP, see e.g., (Saaty,

2004)), conﬂicting criteria (ELECTRE, see e.g.,

(Figueira et al., 2005b)), to synthesise compromise

solutions (TOPSIS, see e.g., (Yoon and Hwang, 1995;

Tadi´c et al., 2014)), as well as to deal with uncertainty

over the judgments (Fuzzy sets theory applied to the

previous methods, see, e.g., (Chen et al., 1992)). Even

though the AHP is one of the most widely MCDM

method used in the literature, we employed it as it

is particularly useful for evaluating complex multi-

attribute alternatives involving subjective criteria to

capture stakeholders’ knowledge of phenomena un-

der study. Basically, AHP consists of the following

main steps.

Build up the Criteria/Alternatives Tree. In this

step the analyst identiﬁes the criteria that com-

pose the decision problem and structure them in a

hierarchical fashion, so that a criterion may have

sub-criteria, and so on. The leafs of this tree are

the alternatives that the decision process aims at

selecting.

Pairwise Comparison. In this step the stakeholders

are required to perform a pairwise comparison of

each criterion at each level of the hierarchy, and

the results are collected in a matrix summarizing

the local priorities for each domain-expert. The

main intuition here is that it is easier (and more

accurate) to compare the importance of two crite-

ria at a time than simultaneously evaluating all of

them. AHP uses the Saaty’s 1 to 9 scale to per-

form the pairwise comparison, the scale ranges

from equal important (1) to extreme important (9)

and allows expressing the intensity of importance

of a criterion over another. It is worth noting two

relevant characteristics of AHP. First, the same

preference scale is used to perform the evaluation

of both (quantitative and qualitative) criteria and

alternatives. Second, the expert does not provide

any numerical absolute judgement; instead a com-

parative evaluation is used, which is more familiar

to people.

Comparisons are recorded in a positive reciprocal

matrix, in which a

represents the comparison be-

tween element i and j.

ApplyingtheAHPtoSmartMobilityServices:ACaseStudy

355

P =







1 a

1,2

··· a

1,n

= 1/a

1 ··· a

2,n

n,1

n,2

··· 1







The rationale of the relationship a

= 1/a

that if A is 4 times more important than B, then

B is 1/4 important with respect to A. Thus, if

the matrix is perfectly consistent, the transitivity

rule is satisﬁed for all the comparisons, namely

= a

· a

. Intuitively, it is expected that if A

is moderate important (3) than B, and B is weak

important (2) than C, thus a consistent judgment

would have that A is 3 · 2 = 6 strong important

than C. One should observe that the inconsisten-

cies are natural in human judgments, for this rea-

son AHP supports the computing of the consis-

tency ratio (see (Saaty, 1977; Ishizaka and Labib,

2009) for more details). It was proved that in-

consistencies in answers can be tolerated if the

consistency ratio remains within a small interval,

that is 10%, see (Saaty, 1977; Ishizaka and Labib,

2009).

Synthesise Global Priorities. The last step requires

to synthesise the global priorities (i.e. the prior-

ity vector) from the pairwise comparisons to de-

termine the ranking of alternatives, taking into

account the stakeholders judgments as a whole.

Mathematically speaking, the priority vector is the

solution of an Eigenvalue problem over the ma-

trix previously introduced. The results of the pair-

wise comparisons are arranged in a matrix. The

ﬁrst (dominant) normalised right Eigenvector of

the matrix gives the ratio scale (weighting) while

the Eigenvalue determines the consistency ratio.

2.1 AHP - Strong and Weak Points in

our Scenario

Here we report some strong points of AHP that make

it the best choice for our purposes.

First, it is ﬂexible, intuitive and it derives ratio

scales from paired comparisons of criteria, thus allow-

ing small inconsistencies in judgments, as we speci-

ﬁed above.

Second, since the problem is arranged into a hi-

erarchical structure, the importance of each element

becomes clear to whom will make the judgment, and

this facilitates the pairwise evaluation of criteria bear-

ing in mind different decision goal contexts.

Third, it has been implemented into an on-line

and free platform

as a supporting tool for decision

http://www.bpmsg.com/academic

making processes. There are however some criti-

cal points that one should address while using AHP.

First, while on the one side AHP allows combining

group judgments for obtaining a global one, on the

other side the use of aggregation function to combine

a high number of group judgments makes possible to

lose some relevant information. To stem this effect,

we identiﬁed three groups of stakeholders on the ba-

sis of their characteristics, namely Service-Providers,

users and young users. This would allow us hav-

ing a ﬁne-grained analysis of the weighted criteria of

each group, as it will be clariﬁed later. Furthermore,

another weak point of AHP relies on the number of

pairwise comparisons that grows exponentially in the

number of criteria to be evaluated. To avoid this, the

number of criteria have been carefully selected and

limited to 8 to prevent the stakeholders being over-

loaded of questions.

3 AHP FOR INNOVATING A

SMART-MOBILITY SERVICE

Figure 1 shows the AHP model we have built.

The criterion Accessibility and Usability focuses

on the (main) features that a smart transportation ser-

vice should provide to users. Thus, all its sub-criteria

have to be read by looking at a user-perspective, that

is: ”A user should be able to perform:”

Online Registration. Service/platform registration

doesn’t require going to a speciﬁc physical

location. Notice that this feature is far from

trivial, as some services require to meet the user,

to check her/his driving licence, and to get a

driving licence photo-copy.

Presence of Smart-card. The service-smart card is

used to access the service (e.g., car-sharing ser-

vices often uses smart-cards to recognise the user,

underground pass-card, etc).

E-ticket. Electronic tickets (e.g., mail, QR-code,

loading money to a card) can be used instead of

printed ones. This sub-criterion differs from the

previous one since in some cases a user may use

the smart-card but may not remotely load money

on it (e.g., access to physical totems is sometimes

required).

Onboard Travel Planner. It refers to the ability to

plan the route from my actual position to the de-

sired one, and this includes the proposition of sev-

eral routes to the user on the basis of both con-

gestion and user-preferences (e.g., minimise plan

time, number of transfers, walking meters, etc.)

DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications

356

Research

Goal

Accessibility and Usability

User Engagement

Services Integration

Online Registration

Presence of Smart

Card

e-ticket

Onboad Travel

Planner

Self-Service

Online-Payment

Onboard Trafﬁc Info

Online Trafﬁc Info

WebSite

Newsletter

Social-Networks

Activity

Mobile-App

Extensiveness

Exchange

Integrated Ticket

Integrated News

Portal

Figure 1: The AHP model. Notice that the node Research Goal refers to ”which are the enabling factors for innovating a

smart-mobility service?”

Self-Service. Tickets can be autonomously pur-

chased, without any human intervention, indepen-

dently of the modality through which the purchase

is realised (e.g., through totems, website, Mobile-

App, etc.).

Online Payment. Deal with all the payment issues

through an online service. This includes recharg-

ing prepaid cards with money, to access the trans-

actions history, to download invoices, and to

add/remove credit-cards, too.

Onboard/Station Trafﬁc Info. Service trafﬁc and

network congestion information are provided

throughphysical devices, using e.g., screen within

the bus/train/car or informative totems placed in

the stations.

Online Trafﬁc Info. Access to all service trafﬁc

and network congestion information is provided

through Internet based services, namely Social-

Network, Websites, Mobile-Apps, etc.

The ”user engagement” criterion would identify

all the main channels that allows to engage the user.

For the sake of clarity we would clarify the meaning

of this term, as it is nowadays abused and it may be

misleading. Here the term engagement includes all

the instruments, services and tools that allows obtain-

ing ”a desirable - even essential - human response to

computer-mediated activities” (Laurel, 2013). In this

direction, we identiﬁed the following features that an

innovative smart-mobility service should have to en-

gage users: Web Site, Newsletter, intensive Social-

Networks Activities, and a Mobile-App. As the mean-

ing of these services are very common concepts, we

omit to specify each of them.

Finally, the Services Integration criterion has been

identiﬁed as it is strongly related to the concept of in-

termodality, that refers to the joint use of several (and

different) transportation services. Being able to re-

alise such a service actually represents a challenge in

the context of smart mobility where several operators

are involved. Within this criterion, we can distinguish

between the following sub-criteria.

Extensiveness. Here intended as the ability to cover

the whole city territory, Milan in such case. No-

tice that this information is intentionally quali-

tative rather than quantitative (i.e., no extension

measures or granularity information has been pro-

vided) to capture the expert’s opinion about the

importance of a full coverage when providing a

city smart-mobility service, in spite of its granu-

ApplyingtheAHPtoSmartMobilityServices:ACaseStudy

357

larity.

Exchange Between Services. To establish a geo-

graphical coordination among the mobility ser-

vices provided in the area, so that users can switch

between services easily and quickly.

Integrated Ticket. Being able to use the travel ticket

across several transportation services. This char-

acteristic becomes quite important in case of pub-

lic and private services integration. To give an ex-

ample, having one travel ticket that gives access

to all public transportation services (e.g., subway,

buses, trams, trains) and private ones (e.g., bikes,

car sharing) would really contribute in improving

and increasing the usage of smart-mobility ser-

vices within the City.

Integrated News Portal. Having a uniﬁed web-

portal that provides all the information about the

city transportation services is probably the most

(challenging) issue to be dealt. Clearly, this portal

would be easy to be realised by public operators

as they can straightforward include trafﬁc news

on trains, subways, trains, buses etc. Conversely,

this is hard to be done by private operators, that

should exchange their information about cars and

bikes positioning as well as vehicles reservation.

Finally, merging both public and private opera-

tors into one informative service could be a re-

ally challenging task as because a permanent in-

formation exchange process should be established

among operators that might be competitors (e.g.,

the operators may lose users accesses to their own

platforms in favor of the integrated portal).

4 RESULT COMMENTS

Once the hierarchical model of criteria and sub-

criteria has been built, we can proceed through the

pairwise comparisons of each criteria and sub-criteria

as described in Sec. 2. To this end, we recruited three

distinct groups of mobility stakeholders, namely

Service-Providers

and users. The latter has been

split into two subgroups: under 35 years-old and

over 35 years-old. We compared the priorities

synthesised by the AHP process through the pairwise

comparisons for each sub-criterion of Fig. 1. The

results of each service-provide judgments are shown

in Tab. 2. The results have been arranged into a series

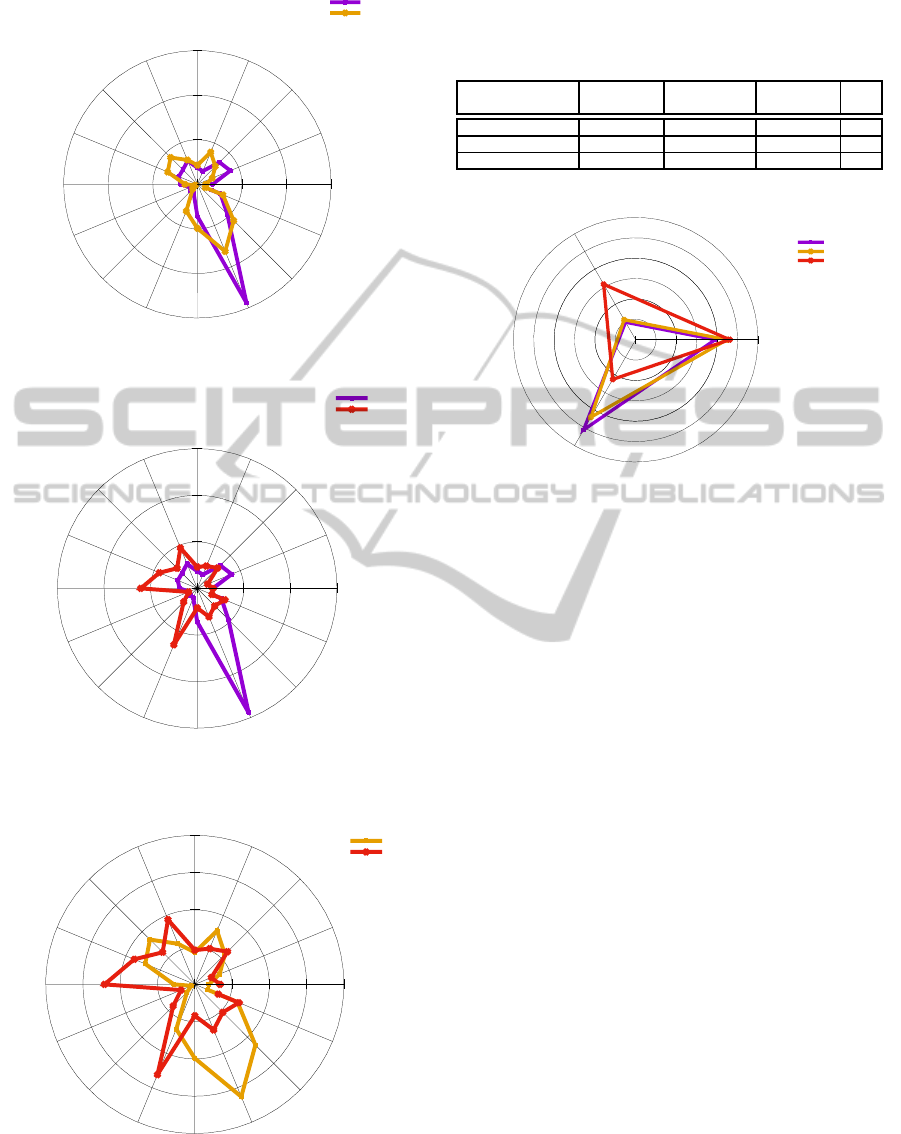
of radar plots where the following can be observed:

This group is composed by stakeholders of mobility ser-

vices in Milan, that includes a subsidiary company, a public

agency, a private operator, and the Municipality of Milan

Service-providers vs Over 35. Figure 2(a) shows

the results for these two groups of stakeholders

showing that both Service Providers and Over

35 users agree in considering the Services Ex-

change as the most important factor for innovating

a smart-mobility service, but the relative weights

are quite different (i.e., 30% and 16% respec-

tively). The shapes depicted in Fig. 2(a) over-

lap for the great part, and this reveals these two

groups of stakeholders weight in a similar way all

these sub-criteria.

Service-providers vs Under 35. The Figure 2(b)

shows that the Under 35 users give to Services

Exchange less importance than MobileApp,

WebSite and Online Payment that represent

the sub-criteria of the User-engagement and

Accessibility and Usability. Here a gap - in terms

of point of views - emerges between these two

targets of stakeholders: while on one side Service

Providers and Over 35 users rank sub-criteria

similarly although with different weights, on the

other side the rank of criteria provided by Under

35 group diverges signiﬁcantly. This result could

be explained by the age gap: considering the raw

judgments shown in Tab. 2, the service providers

group is mostly composed by people older than

35 years (namely, SC, A, and M in Tab. 2). Only

the Private service provider (P) is younger than

35 years, and its ranked sub-criteria are quite

similar to the ones belonging to the Under 35

cluster. This dynamic is highlighted by the radar

plot in Figure 2(c), where only the sub-criteria

weighted priorities of Under 35 and Over 35

users are provided.

Weighted Criteria. In Fig.3 we show a radar plot of

the weighted criteria for each group. Still in this

ﬁgure the age gap among groups can be used to

explain the different point of views on the im-

portance given to the enabling factors for inno-

vating smart-mobility services. Indeed, both ser-

vice providers and Over 35 users consider the Ser-

vice Integration criterion the most important fac-

tor for innovating a smart-mobility service, then

Accessibility and Usability account for the 44.8%

and 46.1% respectively while the User engage-

ment criterion seems to have a very low impor-

tance (about 10% for both). Conversely, the under

35 users give importance to Accessibility and Us-

ability then to the User Engagement and the Ser-

vice Integration criterion account only for 22%.

In Tab.1 we also report the relative weights that

each group assigned to each criterion, including the

average consensus reached amongst groups.

DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications

358

0 10 20 30

Online Reg.

Smart

e-ticket

Onboard TP

Self-Service

Online-Paym.

Onboard Traffic Info

Oline Trattic Info

WebSite

NewsLetter

Social-Network

MobileApp

Extensiveness

Service Exchange

Integr. Ticket

Integr. NewsPortal

Service Providers

Over 35

(a) service providers vs Over 35 users sub-criteria

0 10 20 30

Online Reg.

Smart

e-ticket

Onboard TP

Self-Service

Online-Paym.

Onboard Traffic Info

Oline Trattic Info

WebSite

NewsLetter

Social-Network

MobileApp

Extensiveness

Service Exchange

Integr. Ticket

Integr. NewsPortal

Service Providers

Under 35

(b) service providers vs Under 35 users sub-criteria

0 5 10 15 20

Online Reg.

Smart

e-ticket

Onboard TP

Self-Service

Online-Paym.

Onboard Traffic Info

Oline Trattic Info

WebSite

NewsLetter

Social-Network

MobileApp

Extensiveness

Service Exchange

Integr. Ticket

Integr. NewsPortal

Over 35

Under 35

Figure 2: Sub-criteria pairwise-comparisons.

Table 1: Comparison of stakeholders’ priorities with respect

to the AHP criteria shown in Fig.1. Values in parenthesis

report the average consensus reached amongst each group

participant. All values are in percentage.

Groups Access. User Service CI

& Usab. Engagement Integration

Service-Providers 39 (49.1) 9.9 (43.7) 51.1 (52.9) 2.2

Users > 35 44.8 (58.5) 11.3 (81.8) 43.9 (62.2) 0.4

Users < 35 46.1 (52.8) 31.4 (75.9) 22.5 (70.5) 0.1

0 10 20 30 40 50 0 20 40 60

Accessibility

and Usability

User Engagement

Services Integration

Service Providers

Over 35

Under 35

Figure 3: Comparison of weighted criteria between groups.

For the sake of completeness, in Tab. 2 we provide

the results of the pairwise comparison for each group.

Notice that the AHP allows computing the overall

group results that would summarise the overall group

judgment for a set of criteria (or sub-criteria). Fur-

thermore, we recall that each comparison has ob-

tained a consistency index within the 10%, which is

considered as a limit for obtaining reliable and not

contradictory results (Saaty, 2003).

5 CONCLUSIONS

In this paper we reported our experience in apply-

ing a Multi Criteria Decision Making technique to

the smart-mobility context. Speciﬁcally, we built an

AHP model and we employed three distinct groups

of stakeholders (namely, Service Providers, Under 35

and Over 35 users) to rank the factors for innovat-

ing a smart-mobility service in city of Milan. The

outcome of the AHP is a hierarchy of criteria and

sub-criteria weighted accordingly to the stakehold-

ers preferences. Our outcomes reveal that both ser-

vice providers and over 35 groups preferences are

quite similar, as they both indicate Service Integra-

tion and Accessibility and Usability as the most im-

portant innovating factors while they give low im-

portance to the User Engagement. On the contrary,

for under 35 the Accessibility and Usability grows in

importance at the expense of the Service Integration,

ApplyingtheAHPtoSmartMobilityServices:ACaseStudy

359

Table 2: Results of the pairwise comparisons. SC = subsidiary company ; A = (public) Agency; P = Private Operator; M =

Municipality; U = User.

Cat. Part. Accessibility and Usability User Engagement Service Integration Cons.

Online Reg.

Smart Card

e-ticket

On-board TP

Self-Service

Online-Pay

On-board Trafﬁc

On-line Trafﬁc

Web-Site

News-letter

Social-Network

Mobile-App

Extens.

Exch.

Integ. Ticket

Integ. News Portal

Service Providers

Group 3.4 8 7 3.2 3.7 5.7 4.6 4.5 3.8 1.8 2.1 2.2 7.2 28.8 9.5 5.6 4.1

SC 1.2 3.2 4.9 0.9 1.9 4.3 1.2 2.6 0.2 0.5 3.5 1.3 6.3 47.3 18.1 2.5 10.1

A 1.1 2.8 1.8 3.3 5.7 1.4 7.4 4.3 5.1 1.3 0.3 0.6 2.6 40.4 6 15.8 6.4

P 12.3 9.8 1.9 4 1 6.4 2.6 2.2 6.6 1.6 3.6 8.2 3 17 10 10 0.6

M 4.5 15.2 22.8 2.2 5.8 4.9 11.3 1.6 5.1 1.6 0.9 0.6 15.3 5.8 1.7 0.8 6.2

Users over 35

Group 1.9 3.6 5.7 7.8 4.3 5.9 8.5 7.2 2.8 0.5 1.5 6.5 9.9 16.3 11.5 6.2 1.8

U 6.4 1.3 1.7 11.4 0.6 1.3 16.1 8.4 1.6 0.2 0.6 2.9 18 19.4 3.2 6.7 4.5

U 1 3.7 1.2 4.6 2.5 1 6.2 6.1 13.7 1.5 5 34.4 3.5 10.5 3.5 1.4 2.1

U 11.8 8.7 6.5 2.8 4 16 1.8 17 1.3 0.4 3.2 3.2 7.1 2.5 1.6 12.2 8.6

U 0.6 1.4 0.3 4.4 1.4 1.5 5.6 2.6 3.5 0.2 0.6 1.6 5.9 22.9 44.6 2.9 6.5

U 0.3 0.9 1.8 2.7 0.9 3.7 2.1 1.8 3.1 1.4 6.4 17.6 4.9 18.5 24.2 9.5 1.3

U 1.8 3.1 4.8 8.5 10.8 3.3 13.3 1.1 1.3 0.3 0.5 4.5 5.4 28.5 11 1.8 2.2

U 0.9 5.3 11.1 8.8 11.3 6.7 9.3 4 1.3 0.2 0.5 4.5 3.7 12.5 8.2 11.7 3.5

U 1.7 1.1 14.2 5.7 4.1 11.9 17.1 14.5 4.2 0.3 0.4 2.4 6.9 9.5 5.4 0.8 1.4

U 1.4 13.5 6.7 7 15.8 4.6 10.9 2.6 3.8 0.6 1.7 7.6 9.3 9.6 3.1 1.9 0.4

U 0.6 1.2 3.7 6.5 0.6 3.6 1.5 7.9 1.9 0.4 0.6 7.6 17.3 7 5.1 34.4 4.7

U 1.3 7.4 4.9 4.3 12.8 19 2.9 19.5 2.1 0.4 0.4 4.4 11.5 2.5 4.9 1.5 3

U 0.3 0.7 9.6 2.6 0.5 1.9 3 2.5 0.5 0.2 2.3 2.3 2.3 18.1 47.8 5.5 8.7

Users under 35

Group 3.4 2.4 6.2 5.2 4.6 9.4 6.1 8.8 12.1 2 4.1 13.1 4.2 6.6 5.3 6.4 1

U 5.9 1.9 12.5 1.7 3.9 15.1 1.9 26.8 2.1 0.2 2.1 2.1 3.7 3.7 5.6 10.8 2.3

U 1.5 2.9 2.3 5.3 6.4 3.5 18.7 13.4 17.3 6.9 2 3.6 4.4 7.8 1.1 3 1.5

U 0.5 0.4 2.3 2.4 1.9 2 2.4 2.4 13 3.2 16.9 24 3.2 6.3 6.3 12.7 0

U 5 1.6 13.7 1.4 1.6 21.5 1.3 3.8 7 1.7 5.6 25.3 1.6 0.8 1 7.1 2.6

U 6.8 1.7 3.4 3.2 7.5 20.2 4.1 3.9 9.7 1.5 4 22.7 4.8 1.4 0.7 4.4 1

U 2.4 1.1 1.8 9.3 1.4 3.9 13.1 12.8 15.6 2.7 1.1 2.7 1.7 7.6 12.2 10.4 1.7

U 2.5 4.8 2.5 1.2 1 6.9 1.8 0.5 45 2.2 7.4 15.8 0.9 4.8 2.3 0.4 5.8

U 2.6 1.4 1.2 8.7 2.8 1.8 12.7 8.7 3.9 0.8 5.7 9.6 13.3 12.3 10 4.4 2.2

U 1.1 2.2 21.2 12.6 2.6 7.3 3.5 5.2 4.9 0.6 1.5 5.1 2.7 13.1 11.3 4.8 1.5

U 3.2 1.2 9.6 2.8 4.8 14.5 0.9 7.5 14.2 2.2 2.3 30.2 2.2 1.1 2.9 0.6 1.1

U 1.3 1.4 2.2 3.1 6.2 1.9 7.5 7.6 5.3 0.8 0.8 12.6 3.2 16 8.6 21.5 2.5

whilst the User Engagement criterion becomes quite

important (30%) for them. Concluding, this knowl-

edge could strongly integrate and support sense mak-

ing from large amount of data collected about smart-

mobility service usage, and it describes the dynamics

that guide the stakeholder decision. In our opinion,

using this knowledge with common BI analytics (such

as service usage patterns identiﬁcation, forecasting,

process mining, etc.) could be beneﬁcial for improv-

ing service effectiveness.

REFERENCES

Abdi, M. R. and Labib, A. W. (2003). A design strat-

egy for reconﬁgurable manufacturing systems (rmss)

using analytical hierarchical process (ahp): a case

study. International Journal of Production Research,

41(10):2273–2299.

Bello-Dambatta, A., Farmani, R., Javadi, A., and Evans,

B. (2009). The analytical hierarchy process for con-

taminated land management. Advanced Engineering

Informatics, 23(4):433 – 441. Civil Engineering In-

formatics.

Chen, S.-J. J., Hwang, C.-L., Beckmann, M. J., and Krelle,

W. (1992). Fuzzy multiple attribute decision making:

methods and applications. Springer-Verlag New York,

Inc.

Figueira, J., Greco, S., and Ehrgott, M. (2005a). Multiple

criteria decision analysis: state of the art surveys, vol-

ume 78. Springer Science & Business Media.

Figueira, J., Mousseau, V., and Roy, B. (2005b). Electre

methods.

Ishizaka, A. and Labib, A. (2009). Analytic hierarchy pro-

cess and expert choice: Beneﬁts and limitations. OR

Insights, 22(4):201–220.

Laurel, B. (2013). Computers as theatre. Addison-Wesley.

Madas, M. A. and Zografos, K. G. (2008). Airport ca-

pacity vs. demand: Mismatch or mismanagement?

DATA2015-4thInternationalConferenceonDataManagementTechnologiesandApplications

360

Transportation Research Part A: Policy and Practice,

42(1):203 – 226.

Manville, C., Cochrane, G., Cave, J., Millard, J., Ped-

erson, J. K., Thaarup, R. K., Liebe, A., Wiss-

ner, M., Massink, R., and Kotterink, B. (2014).

Mapping smart cities in the eu. available at:

www.europarl.europa.eu/studies.

Nam, T. and Pardo, T. A. (2011). Conceptualizing smart

city with dimensions of technology, people, and in-

stitutions. In Proceedings of the 12th Annual Inter-

national Digital Government Research Conference:

Digital Government Innovation in Challenging Times,

pages 282–291. ACM.

Saaty, T. L. (1977). A scaling method for priorities in hier-

archical structures. Journal of mathematical psychol-

ogy, 15(3):234–281.

Saaty, T. L. (1988). What is the analytic hierarchy process?

Springer.

Saaty, T. L. (1990). How to make a decision: the analytic

hierarchy process. European journal of operational

research, 48(1):9–26.

Saaty, T. L. (2003). Decision-making with the ahp: Why is

the principal eigenvector necessary. European journal

of operational research, 145(1):85–91.

Saaty, T. L. (2004). Fundamentals of the analytic network

processmultiple networks with beneﬁts, costs, oppor-

tunities and risks. journal of systems science and sys-

tems engineering, 13(3):348–379.

Tadi´c, S., Zeˇcevi´c, S., and Krsti´c, M. (2014). A novel hybrid

mcdm model based on fuzzy dematel, fuzzy anp and

fuzzy vikor for city logistics concept selection. Expert

Systems with Applications, 41(18):8112–8128.

Wu, W.-W. and Lee, Y.-T. (2007). Selecting knowledge

management strategies by using the analytic network

process. Expert systems with Applications, 32(3):841–

847.

Yoon, K. P. and Hwang, C.-L. (1995). Multiple attribute

decision making: an introduction, volume 104. Sage

Publications.

ApplyingtheAHPtoSmartMobilityServices:ACaseStudy

361