
Design of Robust Control Strategy for Non-linear Multivariable
Systems with Delay, Parametric Uncertainty and
External Disturbances
Jose Jorge Carreño Zagarra and Rodolfo Villamizar Mejía
Universidad Industrial de Santander, Cra 27 # 9, Bucaramanga, Colombia
1 RESEARCH PROBLEM
Historically, the process industry has recognized the
important work of automatic control in the proper
functioning of the production process. Although the
preferred control strategy in most applications is the
implementation of simple PID control loops
(Proportional-Integral-Derivative), there are a
number of characteristics which sometimes are not
considered explicitly in the design of these PID
controllers, such as delays, unmeasurable variables,
parameter uncertainty, time variant systems,
nonlinearities, constraints and multivariable
interactions. Many developments of modern control
theory are designed to face up these features, but the
industry has been conservative in applying these
tools. This has led many critics to say that there is a
gap between theory and practice of control.
In industry, many processes are behind in their
dynamic behavior. Although these delays are due
primarily to dynamic characteristics of some
systems, they may also be made by processing time
or the accumulation of time delays in a number of
simple dynamical systems connected in series.
Typical applications in the presence of delays are
communication systems, chemical processes,
transportation systems, power systems, tele-
operation systems and bio-systems.
From classical control perspective, the presence
of delays in a system helps to reduce the phase
margin and hence profit margins, achieving even
destabilize the closed loop response. However, the
introduction of a delay may be beneficial to achieve
stability in an unstable system (Stépán, 1989), which
explains the five decades of interest in the stability
and control of these systems (Stépán, 1989), (Bellm,
1963), (Datko, 1978), (Hale, 1993), (Diekmann et
al., 1995). (Niculescu, 2007), (Niculescu, 2001).
Furthermore, due to the difficulty of accurately
model a complex process, there are always modeling
errors. The development of methods to address the
problem of model uncertainty is a big challenge and
today there have been different approaches to tackle
it. Sometimes, in an attempt to take into account all
relevant dynamics and reduce modeling error, it
comes to the development of increasingly complex
models. However, this maneuver can lead to models
that are too difficult for mathematical analysis and
design of controllers.
Another common problem in the control systems
is due to external disturbances. Such disturbances
bring harm to the system performance, so rejection
is one of the key objectives in the design of the
controller. In control community of Industrial
processes - like oil and metal industries - the
production processes are usually influenced by
external disturbances such as variations in raw
material quality, production load fluctuations, and
variations of complicated production environments.
In the regulation of blood glucose in diabetic
patients, for example, external disturbances are
related to food intake, physical activity conducting
and stress, among others.
In this work, a new control strategy that
combines the virtues of control techniques MPC
(Model Predictive Control), QFT (Quantitative
Feedback Theory) and Disturbances Observers
(DOB) is proposed, in order to address delays,
parametric uncertainty in the model and external
disturbances of nonlinear multivariable systems. It is
intended that the proposed scheme be as simple and
practical as possible and that is validated in at least
two cases of multivariable systems, which can be
active power control in a wind turbine, the automatic
regulation of glucose levels in patients with type 1
diabetes mellitus (T1DM) and / or control of various
variables of quality in a crude distillation process.
2 OUTLINE OF OBJECTIVES
The overall objective of the PhD work is to improve
the dynamic performance of multivariable nonlinear
systems in the presence of delays, external
34
Carreño Zagarra J. and Villamizar R..
Design of Robust Control Strategy for Non-linear Multivariable Systems with Delay, Parametric Uncertainty and External Disturbances.
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
disturbances and parametric uncertainty, by
designing a new control strategy that combines
techniques such as MPC and QFT, and observer
disturbances.
To meet the overall goal above the
implementation of the following specific objectives
are planned:
Solve the problem of designing robust controllers
to parametric uncertainty and external
disturbances from the use of QFT techniques and
disturbance observer.
Improve dynamic performance of multivariable
control systems delays, through an approach to
predictive control (MPC).
Integrate the capabilities of QFT, MPC and
observer design techniques to obtain a robust
control strategy to parametric uncertainty, delays
and external shocks.
To validate the proposed control strategy in at
least two cases of nonlinear multivariable
systems where problems arise in the delay time,
external disturbances and parametric uncertainty.
Some of these cases may be automatic regulation
of glucose in patients with type I diabetes
mellitus, power control in a wind turbine and / or
control various variables in a crude distillation
process.
3 STATE OF THE ART
With the purpose of studying the possibilities that
can address the problems of control, a review of the
results in the control of systems with delays,
parameter uncertainty and external disturbances is
carried out. Then, a review of robust predictive
control as a promising solution is done and the basis
of the alternative solution proposed in this research
is explained afterwards.
3.1 Dead-time
Dead time is the property of a physical system by
which the response to an applied force (action) is
delayed in its effect (Stépán, 1989). Whenever the
material, information or energy are physically
transmitted from one place to another, there is a
delay associated with the transmission. The control
of these delays has been of great interest because
they are the main cause of instability and poor
performance in control systems, such as chemical
processes, long transmission lines in pneumatic
systems, among others (Camacho, 2007).
There are various sources of delay; one of these
sources is the nature of the system, in other words
the way it works. For example, in chemical reactors
there is a finite time reaction and, in an internal
combustion engine a time period is required to mix
air and fuel. Another source of dead-time is the
delay of transport due to the fact of carrying material
through heat or mass transfer systems, as in a
heating system where the transport delay occurs
because of hot air. A delay could also be present in
the communication between the parts of the system,
for example, it takes time for signals to travel
between controllers, sensors and actuators in any
closed-loop system characteristic, particularly in
control systems network and high availability
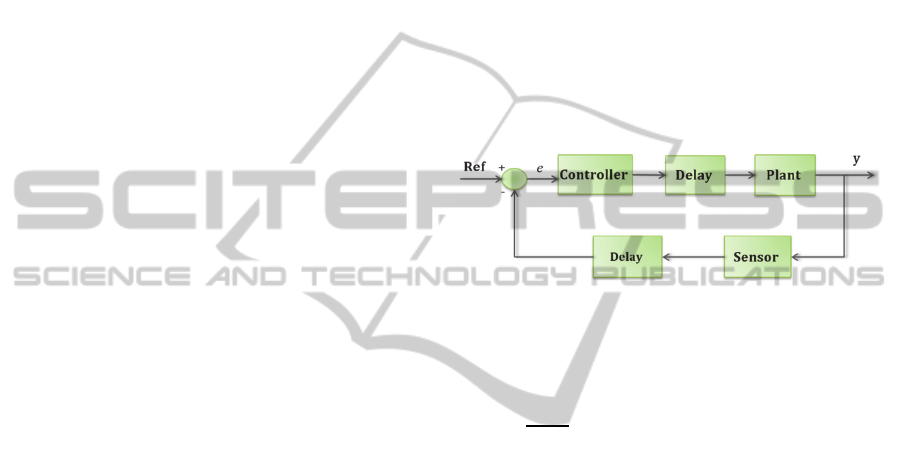
systems (Figure 1).
Figure 1: Delay in a feedback system.
A system with multiple delays in the state vector
can be represented as:
(1)
Where is the n-dimensional state variable,
,
with i=0,1,…,N, is an nxn matrix size and N is a
positive integer.
is the delay, which causes
not only depends on
at time t but also of
the time instants
.
Moreover, the characteristic equation of
Equation (1) is given by:
;
,
,…
0
(2)
Due to the presence of exponential terms, Equation
(2) is a quasi-polynomial and a transcendental
equation, which has an infinite number of roots in
the complex plane . Therefore, Equation (1) is
asymptotically stable if and only if all the roots of
the above equation are in the right half of axis.
Verifying the asymptotic stability of Equation (2)
can be difficult since it has an infinite number of
characteristic equations.
3.1.1 Synthesis of Controllers
It is becoming increasingly clear that delays are a
major cause of instability and poor performance of
DesignofRobustControlStrategyforNon-linearMultivariableSystemswithDelay,ParametricUncertaintyandExternal
Disturbances
35

dynamic systems, added to which are frequently
found in various engineering and physics systems.
The stability analysis and control design of systems
with time delay have attracted the attention of many
researchers (Kolmanovskii et al., 1999), (Silva and
Datta, 2005), (Senthilkumar, 2010). The difficulty of
controlling these processes is due to the fact that
downtime causes a phase delay which decreases the
phase margin deteriorating both performance and
system stability.
3.1.2 PID Controllers
Due to the low cost and easy implementation, most
of controllers used in industry are based on classical
control schemes (Hägglund, 2009), (Takatsu and
Itoh, 1998). In this approach the idea is to compute
the parameters of the controllers considering the
inherent delay to the process. The design problem is
to reduce the design conditions too conservative
(Silva and Datta, 2005). In (Oliveira et al., 2009),
(Hohenbichler., 2009), (Termeh., 2011) can be
reviewed contributions in the design and
implementation of PID controllers in systems with
time delays; specifically in (Yuan-Jay et al., 2011)
we can study the case for variable delays, and in
(Sala and Cuenca, 2009) Application of PID
controllers are presented with dynamic adaptation of
its parameters based on the measured delay.
Although many processes can be controlled by
PID controllers, they have many limitations.
Consider, for example, unity feedback system of
Figure 2, with transfer function of the plant as:
1
(3)
Figure 2: Feedback control scheme.
And PID control as:
1
1
(4)
The transfer function in closed loop would be given
by:
1
1
1
1
(5)
and the characteristic equation of the closed loop
system is:
1
1
0
(6)
Because it is a transcendental equation becomes
difficult to analyze the stability of the system or
design a controller to ensure stability. To reduce the
analysis, we assume that it is a PI controller with
. Then, the transfer function of the closed
loop becomes:
(7)
This system is stable only when
0
2
(8)
Therefore, the controller gain is limited by the length
of the delay: the greater the delay, the lower the
maximum allowable gain and thus a slower response
is obtained.
3.1.3 Dead Time Compensation (DTC)
Control schemes for dead time compensation can be
classified into two types: the Smith Predictor and
Finite Spectrum Assignment (FSA, for its acronym
in English). In 1959 Smith Predictor (Smith., 1959)
is proposed in order to design controllers that allow
isolate the feedback loop delay, thereby enabling to
obtain significant simplifications in the system
analysis and design of the controller.
Figure 3 shows the diagram of a control system
based on the Smith Predictor.
represents the
controller
is the plant or process
being controlled and
1
Smith
predictor.
Figure 3: Control system based on the Smith predictor.
Assuming no perturbations in the system, the
transfer function of the closed loop is given by:
1
(9)
Although you can see that this configuration allows
controller design regardless of the delay has some
significant limitations, such as not being able to be
applied to unstable processes, it has great sensitivity
ICINCO2015-DoctoralConsortium
36

to modeling errors and external disturbances and
only applies to systems with constant delay and
entry (i.e., not applicable to systems with retarded
state) (Zhong, 2006).
In order to overcome some limitations of Smith
Predictor in 1974 the technique of finite spectrum
allocation was developed. This new approach is not
only useful for the design of controllers for unstable
systems with delay but also such delays can be of
input or in the states (Manitius and Olbrot, 1979).
This technique is based on the transformation of
the state vector of the process in order to eliminate
delays of the characteristic equation of the system so
that the closed-loop poles can be allocated from the
required specifications of design (Furutani, 1998).
This method requires no prior knowledge of the
spectrum of the plant, only requires to be assigned n
spectral points while the others left are automatically
deleted (Artstein, 1982).
Consider a system described in state space as:
;
(10)
Then, the transfer function of the plant is:
0
(11)
Finite Spectrum Assignment (FSA) adopts the
following feedback control law:
(12)
The state predicted
is given by:
(13)
Similar to the control scheme based on predictor, the
delay term is removed from the design process. The
resulting closed-loop system is stable if si is
stable. However, the resulting controller cannot be
expressed in the form of Equation (13), to require
additional terms, increasing the controller
implementation effort.
Although DTC structures are more complex and
require greater knowledge for tuning than traditional
PIDs, these have a better compensation for delays,
especially when downtime of process is dominant
(Camacho, 2007). However, because the state
prediction is made from the model, these techniques
have a high sensitivity to modeling errors, especially
when the delay is very large. If a high order model
with delay to describe the dynamics of a process is
needed, both a primary controller of higher order in
the DTC as a traditional (different PID) controller
are needed. In these cases it is clear that the
limitations on the performance of PID are due to
model order and not to delay (Camacho, 2007).
3.1.4 Sliding Mode Control
The technique of sliding mode control (SMC) is a
good alternative for robust stability to uncertainty in
model parameters, non-linearities and external
shocks. This approach provides rapid response and
asymptotic stability and has two main advantages: a)
when the state is limited by the sliding surface can
completely reject SMC uncertainties; b) high
possibility of stabilizing some nonlinear complex
systems which are difficult to stabilize by feedback
law states. Due to these advantages the theory of
sliding mode control has been used in countless
applications (Yu and Kaynak, 2009).
This led to the design studio SMC controllers for
systems with delays at the entrance and / or states
(Richard and Gouaisbaut, 2001). In (Wu et al., 2002)
a control structure on slippery for convergence in
finite systems with input delay time modes is
proposed. In (Roh and Oh, 1999) a sliding surface
based on a predictor that minimizes the effects of
delays system input, and derives a robust control law
that guarantees the existence of a sliding mode and
overcome the delay and uncertainty of the system is
exposed.
As is the case with other conventional control
laws, if when making the design does not take into
account the delay, the system may become unstable
or aggravate the effect of chattering (Sorribes,
Octubre 2011). In (Gouaisbaut et al., 2002) proposes
a methodology to design controllers in sliding mode
based on LMI (Linear Matrix Inequalities) for
systems containing both a delay and multiple delays
and constant or variable delays. The conditions for
the existence of the sliding regime are studied by
using the Lyapunov-Krasovskii functions and
Lyapunov-Razumikhin and LMIs scheme is used in
the optimization procedure.
3.1.5 Model Predictive Control (MPC)
MPC is a powerful technique of control that has
found great acceptance in industrial applications
such as in academia. This success is due perhaps to
the fact that systems be useful both in single variable
and multivariable systems, considering the
restrictions of the control system and inherently
compensate for delays in the process (Ramírez,
2002).
Because of the predictive nature of the MPC
controllers, time delays are considered internally,
property that allows them to be compared with DTC
DesignofRobustControlStrategyforNon-linearMultivariableSystemswithDelay,ParametricUncertaintyandExternal
Disturbances
37

algorithms (Camacho, 2007), (Bordons, 2007). It is
possible to say that each linear MPC can be stated as
a DTC two degrees of freedom when the primary
controller is calculated using an optimization
process. The optimization structure of the internal
DTC is defined as much by the process model as the
model of disturbances and is not dependent of the
optimization procedure even when considering the
restrictions. Figure 4 illustrates this idea.
Figure 4: Outline of model predictive control.
Figure 5 shows the general structure of an MPC
controller predictor for a process with time delay. It
can be seen that the prediction
consists of the
addition of the output of the delay free ideal model
|, and a correction based on the current
plant output and the predicted output |,
passing through a filter.
Figure 5: General structure of predictor MPC.
Although the reference tracking is not dependent
on 1disturbance rejection and robustness of the
closed loop system are directly related to the
predictor filter block MPC. Therefore, these two
characteristics are affected by the dead time of the
process, and in some applications greater scheme is
required.
3.2 Uncertainty
The design of a control system depends significantly
on the dynamic model of the plant or process. As a
real process may be too complex to be described so
absolutely precise by a mathematical model, they
always have modeling errors. The origins and causes
of this discrepancy are many and control theory is
referred collectively as uncertainty in model:
parametric uncertainty, little knowledge of the
dynamics of the process, unknown entries and
dynamic despised and simplifications in the model,
among others (Rodríguez, 1996), (Diederich, 2005).
For example, if a model based on the linearized
about a nominal operating point of a nonlinear
system controller is designed, the nonlinearities are
presented as modeling uncertainties.
In Figure 6 the general outline of feedback
control system in the presence of uncertainty arises.
Es is the uncertainty associated with the model
and G
∗
s represents the actual plant model.
Figure 6: Control system with uncertainty in the plant
model (Rodríguez, 1996).
Items with uncertainty can be classified as
structured uncertainties and unstructured
uncertainties. In the first, sources of uncertainty of
systems are localized, obtaining with this a tighter or
structured modeling errors description. In the
Unstructured uncertainties what is commonly known
is a dimension of the magnitude of the uncertainty,
usually frequency dependent. These complex
uncertainties generally occur in the high frequency
range and may include not modeled time delays,
parasitic coupling, hysteresis and other
nonlinearities. An example of this kind of
uncertainty is presented in the linearization of a
nonlinear plant. If the actual plant is nonlinear and
its model is linear, the difference acts as
unstructured uncertainty (Matušů, 2007).
3.2.1 Control of Systems with Uncertainty
Currently there are two main approaches that try to
overcome the uncertainty in the model: adaptive
control (Slotine and Weiping, 1991), (Bodson, 1989)
based on online identification process and
adjustment of the slider to the desired conditions;
and robust control (Sidi, 2001), (Horowitz, 1992),
(Ortega and Rubio, 2004), which guarantees the
preservation of certain properties of the control loop
ICINCO2015-DoctoralConsortium
38

for the whole family of controlled plants.
Various strategies of adaptive control have been
proposed considering uncertainty SISO and MIMO
systems. Such controllers often involve some type of
functions to approximate the unknown dynamics.
However, the approximation error and disturbance-
internal or external-can impair controller
performance or even destabilize the system of closed
loop control. Therefore, in order to ensure the
performance of the controller, various robust
components are incorporated in the design of
adaptive controllers, resulting in robust adaptive
controllers (Ioannou, 1996), (Moheimani, 2001),
(Wenjie, 2005).
3.3 Disturbances
The problem of disturbance rejection is an eternal
subject of investigation since the introduction of
control theory and applications. From direct design,
the interference rejection, traditional control
methods such as proportional integral derivative
(PID) and linear quadratic regulator controllers
(LQR), may be unable to comply with the
specifications of high precision control in strong
disturbances and uncertainties. The rationale for this
is that these traditional methods do not take into
account explicitly the attenuation of uncertainty or
disruption when controllers are designed.
The typical characteristics of the main
disturbance mitigation methods are summarized as
follows:
Adaptive Control (AC): The idea of adaptive
control is that first the model parameters controlled
online system are identified, and then the controller
parameters are tuned based on that estimate. This
control technique is very effective in the treatment
of model uncertainties and has gained wide
applications in engineering practice. Successful
applications of adaptive control usually rely heavily
on design ID laws or estimate model parameters
variation in time. When these key parameters are
difficult to identify or estimate online, these methods
are not valid.
Robust Control (RC): The robust controller design
considers the worst case of disturbances and model
uncertainties. The robustness of robust control is
usually obtained by sacrificing the transient
performance of other highlights. Therefore, the
robust control is often criticized for being sometimes
very conservative.
Sliding Mode Control (SMC): SMC has fine skills in
suppressing the effects of parameter variations and
external disturbances. However, the discontinuous
switching controller makes it prone to induce
chattering (chattering) of high frequency mechanical
systems. Although the use of some modification
methods such as the method of saturation function
could effectively reduce the chattering problem, the
performance advantage of the disturbance rejection
is sacrificed. These disadvantages significantly limit
SMC applications.
Internal Model Control (IMC): Since the 1980s, the
IMC approach proposed by Garcia and Morari has
been used to mitigate the effects of external shocks
in the control systems. This technique has received
much attention in control theory and various
applications due to its simple concept and intuitive
design philosophy. However, BMI is generally
available for linear systems. Furthermore, the
application of BMI algorithm for high-dimensional
system is quite sophisticated because of the need to
calculate the inverse of a matrix high dimensional
transfer function.
The motivation of the aforementioned approaches of
control is to reject control disturbances of feedback
rather than control feedforward compensation. These
control methods generally achieve the goal of
disturbance rejection through feedback regulation
based on the tracking error between the measured
outputs and set-points (Hohenbichler., 2009).
Therefore, controllers designed can’t react fast
enough and directly in strong disturbance, although
they may ultimately suppress disturbances through
feedback regulation of a relatively slow manner. To
this end, these control approaches are generally
recognized as passive anti disturbs control methods
(PADC).
To overcome the limitations of the PADC
methods in handling the disturbs, it has been
proposed the approach called active anti disturbs
control (AADC). Generally speaking, the idea
behind the AADC is directly counteract disturbances
by the feedforward control of compensation based
on measurements or estimates disturbances.
3.3.1 Control based on Disturbance
Observer
Unlike Passive Anti Disturbs Control (PADC),the
Disturbance Observer Control (DOBC) provides an
active and effective way to deal disturbances and
improves the robustness of the control system in
closed loop. Feedback control and feedforward
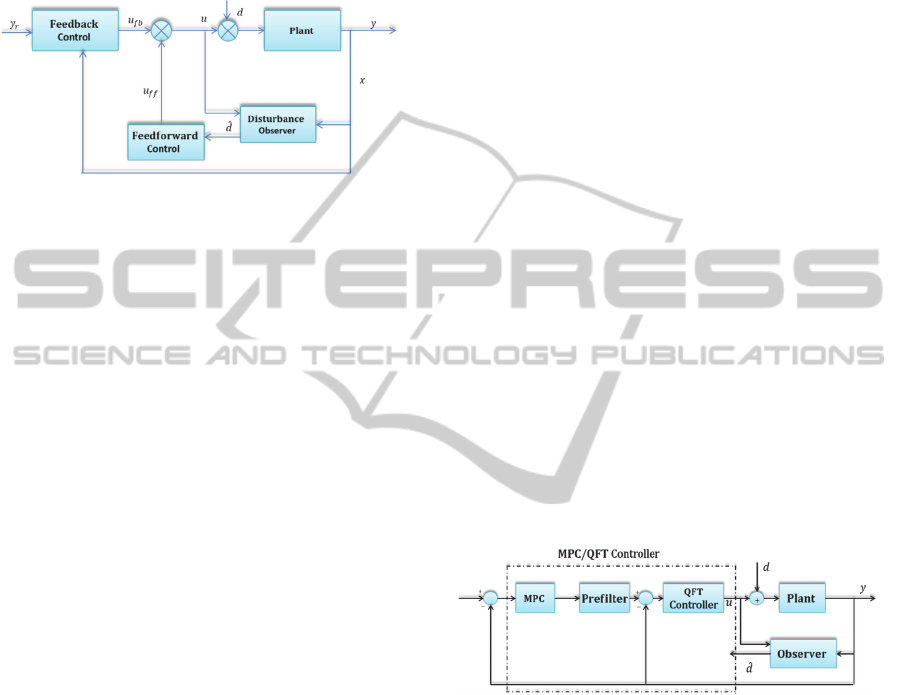
control based on disturbance observer: Figure 7
shows a basic control scheme based on the
observation of the disturbance, the control structure
consists of two parts. Feedback control is generally
DesignofRobustControlStrategyforNon-linearMultivariableSystemswithDelay,ParametricUncertaintyandExternal
Disturbances
39
employed to ensure monitoring and stabilizing the
dynamics of the controlled nominal plant. At this
stage the disturbances and uncertainties not
necessarily need to be considered. These can be
estimated by a disturbance observer to be
compensated by a feedforward controller.
Figure 7: Basic structure of a controller based on
disturbance observer.
The greatest merit of this design approach is that
the combination of feedback control and
feedforward control allows isolating control
performance monitoring with the rejection of
disturbances.
3.4 Robust Predictive Control
From the analysis previously developed, one can
sense that the predictive nature of the MPC
controllers inherently considers time delays, so that
they can be compared with control algorithms for
dead time compensation (DTC). These controllers
have good performance in systems with time delays;
reason derives its widespread use in systems which
perform chemical processes.
Moreover, in plants having model uncertainty,
researchs strongly favor the use of robust controller.
From this point of view, it is not illogical to think
that the combination of two control strategies could
provide the benefits of both systems having different
open problems as nonlinearities, model uncertainty,
delay, external shocks, variance in time, among
others.
In recent years the use of these mixed Control
strategies presented considerable growth for their
welcome in increasingly complex systems.
Therefore, for processes containing exhibit delays
and uncertainty in the model parameters, a control
strategy robust MPC promise satisfactory results
(Ramírez, 2002), (Raimondo et al., 2009),
(Maciejowski, 2000), (Bemporad and Morari,
Robust model predictive control: A survey, 2007).
The MPC control technique MPC Min-Max is a
robust control technique useful for solving problems
caused by the discrepancies in the prediction model
and the real process. Not only minimizes a criterion
that considers the nominal value of the process
output, but also minimizes the maximum value that
can take the objective function from the
consideration of uncertainty in the model. In other
words, the optimal sequence of actions is calculated
as:
∗
min
∈
max
∈
,
(14)
where represents uncertainty and Θ describes the
set of values considered in the uncertainty.
Although the advantages of MPC Min-Max on
the Control MPC nominal technique lie better
control when the dynamic is not described well
enough by the prediction model, this technique has
problems because of the high computational cost
(Bemporad and Morari, 2007).
3.5 Proposed Solution: Control MPC /
QFT based on Disturbance
Observer
As mentioned in the previous point, in the MPC
control area there is a need to seek predictive control
algorithms that besides being robust to model
uncertainties and external disturbances are
computationally efficient on-line. To that end, in this
thesis a scheme of MPC / QFT control based on
observer for multivariable plants is proposed, as
shown in Figure 8.
Figure 8: MPC/QFT controller based on observer.
The scheme consists of an internal QFT
controller that reduces the uncertainty in the plants
family and therefore increases the stability of the
external controller robust MPC. The latter facilitates
the management of dynamic constraints and delays
in the system.
Thanks to QFT uncertainties are taken into
account in a systematic way in order to contain
results without conservatism- property that promises
better results than Robust-Predictive and Adaptive-
Robust techniques. Given these considerations, and
coupled with the difficulty of QFT robust control
technique to manage restrictions, the union of the
QFT and MPC techniques provides a new approach
that turns out to be less sensitive to disruption and
ICINCO2015-DoctoralConsortium
40

uncertainty in the process model, with less
computational load and taking into account the
constraints of the process since MPC has the ability
to include systematically.
In addition, the MPC algorithm control through
the prediction feature allows QFT go forward when
the reference signal is known. The inclusion of
disturbance observer to MPC/QFT scheme
contributes to external disturbance estimation
allowing the control system a better accuracy and
robustness.
4 METHODOLOGY
The development of the research will take place in
the following stages:
4.1 Bibliography Review
At this stage is carefully reviewed the relevant
bibliography on QFT and MPC design control and
disturbance observer applied in multivariable
systems. Besides courses, materials and videos
related to the control approach in order to solve
control problems studied.
4.2 Tackling the Problem of
Parametric Uncertainty in
Multivariable Systems
At this stage the current strengths and limitations of
Quantitative Control Theory QFT in the regulation
and control of multivariable systems with
uncertainty in the model parameters are studied and
will plan an approach to reduce the difficulties.
4.3 Solving the Problem of External
Disturbances
At this stage we study the different types of
observers to cope with external disturbances present
in multivariable processes. Such observers may be
linear, non-linear or non-linear advanced, so the
adequate structure should be carefully reviewed to
solve the problem of estimation and disturbance
rejection.
4.4 Tackling the Problem of Time
Delays
At this stage the representation is obtained in state
space in discrete time of the internal control loop
(consisting of the pre-controller and observer) to
solve the problem of time delays through an
approach based on Model Predictive Control (MPC),
and taking into account systematically the
constraints of the system. Also are adjusted some
parameters of the cost function of the predictive
controller as the forecast horizon, the weighting
factors of the control effort and mean square error
and the sampling period.
4.5 Integration of QFT, MPC and
Observer of Disturbances
At this stage the control QFT and MPC and
disturbance observer approaches are gathered, and
the problem of global optimization is solved by
using techniques based on Lyapunov stability as
Linear Matrix Inequalities (LMI) or heuristics
optimization techniques such as genetic algorithms,
among others.
4.6 Validation of MPC / QFT Control
Strategy in Cases 1 and 2
At this stage is validated the design methodology of
controllers in the regulation of glucose in patients
with diabetes mellitus type I and in another case
such as the power control in a wind turbine or in
controlling various process variables in a crude
distillation.
4.7 Dissemination of Results
The dissemination to the scientific community is
continuously from the time the methodology of
design of controllers is developed. Such disclosure is
for attendance at international events and
publications in recognized journals.
4.8 Final Report
Finally a complete report of the contribution
originated-doctorate level -in this research is made.
5 EXPECTED OUTCOME
Taking advantage of the virtues of robust control
technique and predictive control, the merger of the
two strategies will enable optimum results in
nonlinear systems with parametric uncertainty, and
in the presence of delays and restrictions. Robust
MPC Min-Max controllers are useful for
DesignofRobustControlStrategyforNon-linearMultivariableSystemswithDelay,ParametricUncertaintyandExternal
Disturbances
41

troubleshooting in the discrepancy of the model
parameters and systems with time delays. However,
due to the high computational cost the number of
applications of this technique is relatively small, so
you should delve in the study of robust MPC
different approaches in order to solve this problem.
This research proposed a novel method that
combines the virtues of MPC control techniques
proposed nonlinear QFT and observers of
disturbances (DOB), to address the delays,
uncertainty in the model and external shocks of
multivariable systems. Cascade structure combining
an inner loop containing the nonlinear QFT with an
outer loop controller where a predictive controller
provides the appropriate reference to inner loop is
proposed. This fusion of drivers considered the
estimate made by a disturbance observer to mitigate
the impact of external disturbance.
The results to be obtained in this thesis are:
1. Approach of an alternative solution to the
problem of parametric uncertainty nonlinear
multivariable processes, using the virtues of QFT
nonlinear and making important contributions in
this area.
2. Proposal for an alternative solution to the
problem of external disturbances in multivariable
systems using observer’s theory design.
3. Formulation of a control scheme to work with
time delays and constraints multivariable
systems using predictive control strategy and
discrete delta transform.
4. Approach to technical integration of nonlinear
QFT and MPC Control and Disturbance
Observer to solve the problems of temporary
delay, parameter uncertainty, constraints and
external disturbances in multivariable systems.
5. A comparison and analysis of the results
obtained with the proposed control approach
applied to two cases that have the control
problems studied.
6 STAGE OF THE RESEARCH
Since most physical systems are characterized by
uncertain nonlinear models, it is natural to apply a
linearized approximation of the system because it
replaces the nonlinear uncertain plant by a set of
uncertain LTI plants. However, for operating points
far from the vicinity this procedure may fail.
To work with uncertainty in the model and
nonlinear systems, (Baños and Bailey, 2001)
proposes a non-linear approach QFT. In that
approach an equivalent LTI system is defined by
replacing the nonlinear plant by a set of LTI plants
and a set of attached disturbances De. The
replacement has to be done in such a way that the
LTI equivalent problem has a solution for the
compensators F and G -which are the system
controller, respectively-; and with the goal that this
solution be valid for the original nonlinear problem.
The basic idea is to make both control problems, the
nonlinear and the LTI problem, equivalent with
respect to a particular sets of acceptable
outputs
,
, depending on each particular
combination of references and disturbances.
The thesis currently working on using this
technique nonlinear QFT control to initially validate
their results in regulating glucose in patients with
diabetes. To this end Bergman minimal model which
was proposed for to represent glucose concentrations
and plasma insulin test after intravenous glucose
tolerance (IVGTT). Bergman used to represent these
three compartments concentrations: Plasma insulin I
(t) (mU / L), remote insulin X (t) (mU / L) and
plasma glucose G (t) (mg /dL or mmol/L), and
raised the following differential equations:
∗
(15)
(16)
(17)
Where:
/: is the blood glucose concentration at
time [min];
/: is the blood insulin concentration at
time [min];
: is proportional to the plasma insulin
concentration in a remote compartment function.
/: is the basal glucose level of the patient;
/: is the patient’s basal insulin level.
With this research is expected to use the nonlinear
QFT control scheme to work with nonlinear systems
in the presence of dynamic delays, as presented in
the regulation of glucose and estimating external
disturbances (which for this system would be
glucose intake) through the design of nonlinear
observers. In the outer loop an MPC controller that
deals with the restrictions of the plant and the
existing delay will be designed. In order to do so, it
will obtain the representation in state space in
discrete time of internal loop control using the delta
transformation and the uncertainty of the system will
be considered when solving the problem of global
ICINCO2015-DoctoralConsortium
42

optimization through techniques based on Lyapunov
stability as Linear Matrix Inequalities (LMI).
REFERENCES
Al-Muthairi, M. S. (1994). Quadratic stabilization of
continuous time systems with state-delay and norm-
bounded time-varying uncertainties. IEEE Trans.
Automat. Contr., vol. 39.
Artstein, Z. (1982). Linear systems with delayed control:
A reduction. 4(27).
Ballance, W. C. (1998). QFT Design for Uncertain
Nonminimum Phase and Unstable Plants.
Philadelphia, Pennsylvania: Proceedings of the
American Control Conference.
Barbot, W. P. (2002). Sliding Mode Control in
Engineering. New York: Marcel Dekker.
Bellm, R. a. (1963). Differential-Difference Equations.
New York: Academic.
Bemporad, A., & Morari, M. (2007). Robust model
predictive control: A survey. 245.
Bodson, S. S. (1989). Adaptive Control: Stability,
Convergence, and Robustness. New Jersey: Prentice
Hall.
Boje, E. (2000). Finding Nonconvex Hulls of QFT
Templates. Trans. ASME, VOl. 122.
Bordons, E. F. (2007). Model Predictuve Control. London:
Springer-Verlag.
Camacho, J. N.-R. (2007). Control of Dead-Time
Processes. London: Springer-Verlag London Limited.
Chen, D. J. (1998). Symbolic Computation in Value Sets
of Plants with Uncertain Parameters. Processing
UKACC International Conference Control.
Datko, R. (1978). A procedure for determination of the
exponential stability. 36(279-292).
Diederich, H. a. (2005). Mathematical Systems Theory I:
Modelling, State Space Analysis, Stability and
Robustness. Berlin: Springer Berlin Heidelberg.
Diekmann, O., Van Gils, S., & Verduyn-Lunel, S. a.
(1995). Delay Equations, Functional-, Complex and
Nonlinear Analysis. New York: Springer-Verlag.
Esfanjani, R., Reble, M., Munz, U., Nikravesh, S., &
Allgower, F. (2009). Model predictive control of
constrained nonlinear time-delay systems. IEEE
Conference on Decision and Control, 2009 held
jointly with the 2009 28th Chinese Control
Conference. CDC/CCC 2009. Proceedings of the 48th
Furutani, E. a. (1998). Robust Stability of state-predictive
and Smith Control Systems for Plants with a pure
Delay. 8(18).
Gouaisbaut, F., Dambrine, M. a., & J.P. (2002). Robust
Control of Delay systems: A Sliding Mode Control
Design via LMI. 46(4).
Guzmán, J., Álamo, T., Berenguel, M., Dormido, S., &
Camacho, E. (2007). Robust GPC-QFT approach
using Linear Matrix Inequalities. Kos, Greece:
European Control Conference ECC2007.
Hägglund, K. J. (2009). Control PID avanzado. Madrid:
Pearson Educación.
Hale, K. a. (1993). Introduction to Functional Differential.
New York: Springer-Verlag.
Hohenbichler., N. (2009). All Stabilizing PID Controllers
for Time Delay Systems. 45(11).
Horowitz, I. (1992). Quantitative Feedback Design
Theory. Boulder, Colorado: QFT Publications.
Ioannou, P. A. (1996). Robust Adaptive Control.
University of Michigan: Prentice Hall.
Jin-quan, H., & Lewis, F. (2003). Neural-network
predictive control for nonlinear dynamic systems with
time-delay. IEEE Transactions on Neural Networks .
Kolmanovskii, V. B., Niculescu, S.-I., & Gu, K. (1999).
Delay Effects on Stability: A Survey. Arizona USA:
Proceedings of Conference on Decision & Control.
Maciejowski, J. (2000). Predictive Control with
Constraints. Prentice Hall.
Manitius, A., & Olbrot, A. (1979). Finite spectrum
assignment problem for systems with delays. 24(4).
Martín-Romero, J. M.-R. (2007). QFT Templates for
Plants with a High Number of Uncertainty Parameters.
IEEE Transactions on Automatic Control, Vol. 52,
No.4.
Martín-Romero, J., & García-Sanz, M. G.-M. (2007).
Analytical Formulation to Compute QFT Templates
for Plants with a High Number of Uncertain
Parameters. Athens, Greece: Mediterranean
Conference on Control and Automation.
Matušů, R. (2007). Doctoral Thesis. Robust Control of
Systems with Parametric Uncertainty:An Algebraic
Approach. Zlín, Czech Republic: Tomas Bata
University in Zlín.
Moheimani, S. (2001). Perspectives in Robust Control.
Springer Science & Business Media.
Namaki-Shoushtari, O. a. (2009). Design of Decentralized
Supervisory Based Switching QFT Controller for
Uncertain Multivariable Plants. Shanghai, China: Joint
48th IEEE Conference on Decision and Control and
28th Chinese Control Conference.
Niculescu, S. I. (2001). Delay Effects on Stability: A
Robust Control Approach. Heidelberg: Springer-
Verlag.
Niculescu, W. M.-I. (2007). Stability and Stabilization of
Time-Delay Systems: An eigenvalue approach.
Philadelphia, PA: SIAM.
Olbrot, A. M. (1979). Finite spectrum assignment problem
for systems with delays. 24(4).
Oliveira, V., Cossi, L., & Teixeira, M. a. (2009). Synthesis
of PID controllers for a class of time delay systems.
7(45).
Ortega, M. G. & Rubio, F. (2004). Systematic Design of
Weighting Matrices for the H∞ Mixed Sensitivity
Problem. 14.
Peiwen, Z., & Qiang, Y. Y. (2000). Multivariable QFT
Control of Coaxial Double Brushless DC Motors
System. Proceedings of the 2000 American Control
Conference .
Pop, C., Dulf, E., De Keyser, R., Ionescu, C., Muresan, B.,
& Festila, C. (2011). Predictive control of the
multivariable time delay processes in an isotope
DesignofRobustControlStrategyforNon-linearMultivariableSystemswithDelay,ParametricUncertaintyandExternal
Disturbances
43

separation column. 6th IEEE International Symposium
on Applied Computational Intelligence and
Informatics (SACI)
Raimondo, D. M., Limon, D., Lazar, M., & Camacho, L.
M. (2009). Min-max model predictive control of
nonlinear systems: A unifying overview on stability.
15(1).
Ramírez, D. R. (2002). Control Predictivo Min-Max:
Análisis, Caracterización y Técnicas de
Implementación. Tesis Doctoral. Sevilla: Universidad
de Sevilla.
Richard, J., & Gouaisbaut, F. a. (2001). Sliding Mode
Control in the presence of Delay. 37(3).
Rico, J. &.-M. (2011). Multivariable QFT Robust Control
of a Heat Exchanger. 19th Mediterranean Conference
on Control & Automation (MED).
Rodríguez, F. &. (1996). Control Adaptativo y Robusto.
Sevilla, España: Universidad de Sevilla.
Roh, Y.-H., & Oh, J.-H. (1999). Sliding Mode Control
with Delay Compensation for Uncertain Input-Delay
Systems. 1.
Sala, A., & Cuenca, J. a. (2009). A Retunable PID multi-
rate Controller for a Networked Control System.
14(179).
Sardar, P. S. (2000). Template Generation for Continuous
Transfer Functions using Interval Analysis.
Automatica, vol. 36.
Sbarciog, M., De Keyser, R., Cristea, S., & de Prada, C.
(2008). Nonlinear Predictive Control of processes with
variable time delay. A temperature control case study.
IEEE International Conference on Control
Applications.
Senthilkumar, M. L. (2010). Dynamics of Nonlinear
Time-Delay Systems. New York: Springer.
Shengyuan Xu, P. V. (2002). Robust Stability and
Stabilization for Singular Systems with State Delay
and Parameter Uncertainty. IEEE Transactions on
Automatic Control, Vol. 47, No. 7.
Shijun, T., Wenzhan, D., & Aiping, Y. (2012). An
improved generalized predictive control algorithm
applied in long time-delay system. 24th Chinese
Control and Decision Conference (CCDC) .
Sidi, I. M. (1978). Optimum Synthesis of Nonminimum
Phase Feedback System with Plant Uncertainty.
International Journal Control, 27.
Sidi, M. (2001). Design of Robust Control Systems from
Classical to Modern Practical Approaches. Malabar,
Florida: Krieger.
Sidi., I. M. (1972). Synthesis of Feedback Systems with
Large Plant ignorance for prescribed Time Domain
Tolerances. International Journal Control, 16.
Silva, G., & Datta, A. a. (2005). PID Controllers for Time-
Delay Systems. Texas USA: Birkhauser Boston.
Jean-Jacques Slotine & Weiping, L. (1991). Applied
Nonlinear Control. New Jersey: Prentice Hall.
Slotine, Jean-Jacques & Weiping, L. (1991). Applied
Nonlinear Control. New Jersey: Prentice Hall.
Smith., O. (1959). Closer control of loops with dead time.
53(5).
Sorribes, A. G. (Octubre 2011). Sistemas Dinámicos con
Retardos Temporales. Tesis Doctoral. Valencia
(España): Universitat Polit'ecnica de Val'encia.
Stépán, G. (1989). Retarded Dynamical Systems: Stability
and Characteristic Function. London, U.K.: Longman
Scientific.
Tadmor, G. (2000). The standard Hinf problem in systems
with a single input delay. 45(3).
Takatsu, H., & Itoh, T. a. (1998). Future needs for the
control theory in industries-report and topics of the
control technology survey in the japanese industry.
8(5-6).
Termeh., M. B. (2011). Domains of PID Controller
coefficients which guarantee Stability and
Performance for LTI Time-Delay Systems. 9(47).
Vital, M. G.-S. (1999). Efficient Computation of the
Frequency Representation of Uncertain Systems.
Proceeding 4th Int. Symp. Quantitative Feedback
Theory Robust Frequency Domain Methods.
Wang, W.-Y., Chan, M.-L., Hsu, C.-C. J., & Lee, &. T.-T.
(2002). Hinf Tracking-Based Sliding Mode Control
for Uncertain Nonlinear Systems via an Adaptive
Fuzzy-Neural Approach. IEEE Transactions on
Systems, Man, and Cybernetics, Part B: Cybernetics,
Vol. 32, No.4.
Wenjie, D. &. (2005). Robust Adaptive Control of
Nonholonomic Mobile Robot with Parameter and
Nonparameter Uncertainties. IEEE Transactions on
Robotics, vol. 21, No. 2.
Wu, Y., Gu, J., & Yu, X. (2002). Finite time sliding mode
control for time delay systems. 2.
Xua, S., Lamb, J., & Yang, C. (2001). Quadratic stability
and stabilization of uncertain linear discrete-time
systems with state delay. Systems & Control Letters,
vol. 43.
Ying-Jeh Huang, T.-C. K.-H. (2008). Adaptive Sliding-
Mode Control for Nonlinear Systems with Uncertain
Parameters. IEEE Transactions on Systems, Man, and
Cybernetics —Part B: Cybernetics, Vol. 38, No.2.
Yu, X., & Kaynak, O. (2009). Sliding-Mode Control with
Soft Computing: A Survey. 56(9).
Yuan-Jay, W., Jian-Jie, H., & Yan-Chang, S. S.-H. (2011).
Graphical Computation of Gain and Phase Margin
Specifications oriented Robust PID Controllers for
Uncertain Systems with Time-varying delay. 4(21).
Zhong, Q.-C. (2006). Robust Control of Time-Delay
Systems. Liverpool, United Kingdom: Springer.
Zhong., Q.-C. (2003). On standard Hinf control of
processes with a single delay. 6(48).
Zhou, J., & Zhang, C. W. (2004). Adaptive Backstepping
Control of a Class of Uncertain Nonlinear Systems
with Unknown Backlash-Like Hysteresis. IEEE
Transactions on Automatic Control, Vol. 49, No. 10.
ICINCO2015-DoctoralConsortium
44
